“平行四邊形面積”之難

郜舒竹

【摘? ?要】通常“平行四邊形面積”的教學，是將平行四邊形通過剪拼，轉化為長方形，進而運用長方形面積公式推導出平行四邊形面積公式。事實上，表面看平行四邊形與熟悉的長方形十分相像，其實其中蘊含著認知上的差異，這樣的差異會成為深入理解的障礙，挖掘這樣的差異并融入學習活動設計，可以讓學生有機會體驗用透視、關聯和運動的眼光看待事物。

【關鍵詞】平行四邊形;長方形;面積;穩定性;協變

學科課程教學改革期望“變教為學”，將以教師教的活動為主的課堂教學，改變為以學生學習活動為主的課堂教學，其中一個需要研究的問題是：如何為學生的學習設計活動？任何自主性的學習一定是以學習者已有知識或經驗為基礎的，這樣的知識或經驗對新內容的學習可能產生積極的正面作用，也可能產生消極的負面作用。

因此，教師在備課中需要思考的一個問題是：對新內容學習產生影響的已有知識或經驗究竟是什么？這樣的影響是正面的積極作用，還是負面的消極作用？

一、貌似容易

以“平行四邊形”為例，數學課程中與之最為接近的已有知識和經驗自然應當是“長方形”。二者進行比較，許多方面都有相同和相近之處。從形式上看，都是四邊形;從特性上看，都滿足“對邊平行且相等”。鑒于這樣的相同或相近，往往會感覺平行四邊形以及相關內容的學習并不困難。

事實上，貌似容易的內容往往蘊含著更大的困難。表面看相同或相近的對象，如果仔細挖掘，會發現二者其實存在著巨大差異，這樣的差異就會成為學習過程中理解的難點。

眾所周知，長方形面積公式是“長[×]寬”，直觀上看就是相鄰兩邊長度的乘積（見圖1）。

如果把平行四邊形看作是長方形拓展出來的，形式上相近并且相像的圖形，基于長方形的經驗，自然的想法是：

l平行四邊形面積也應當是相鄰兩邊長度的乘積。

因此對于平行四邊形面積的學習，首先需要對這個想法進行探究，通過辨析的活動否定這個想法。這種辨析就是要回答如下問題：

l一般的平行四邊形與長方形究竟有哪些不同之處？

二、透視的眼光

透視（Insight）的眼光指的是由表及里地看待事物，不僅關注表面，而且能夠透視出感官所觀察不到的內容。相對于長方形，一般的平行四邊形形式上看是“歪”的，通過表面的“歪”，可以透視出平行四邊形與長方形在“確定性（Certainty）”方面的差異。

這里的確定性，指的是構成平面封閉圖形的各條邊，其長度一旦確定，圖形的形狀以及面積大小也隨之確定。對于長方形而言，長和寬的長度一旦確定，則長方形的形狀和面積大小隨之確定，因此長和寬的長度就成為確定長方形形狀和大小的因素。

而一般的平行四邊形并不具備這樣的確定性。比如圖2中兩個平行四邊形，對應邊的長度都是相等的，但其形狀和面積大小都有差異。

這說明，平行四邊形的形狀和大小，與其各條邊的長度不具備確定的因果關系。正是一般平行四邊形面積大小與形狀的不確定性，使得平行四邊形面積不能表達為相鄰兩邊長度的乘積。

一般平行四邊形與長方形第二個差異，反映在面積與其一條邊長的協變關系方面。這里的“協變（Covarience）”指的是，圖形面積大小與其一條邊長具有同增或同減的關系。比如對于長方形，如果一條邊長增加，那么面積一定隨之增加。不僅如此，長方形面積與其一條邊長還具有正比例的協變關系，也就是說，如果長方形一條邊長擴大為原來的幾倍，另外一條邊長不變，那么面積也隨之擴大為原來的幾倍。而一般的平行四邊形不具備這樣的協變關系（見圖3）。

圖3中兩條平行線L1和L2之間有兩個寬度相同的平行四邊形，左側平行四邊形AB邊，對應右側平行四邊形CD邊，而且CD>AB，但兩個平行四邊形面積相等。也就是說，平行四邊形的一條邊長增加，其面積可以不變，甚至可能減小。

這就說明一般的平行四邊形面積不具備與其一條邊長同增或同減的協變關系。進一步說明了平行四邊形面積大小并不由邊的長短所確定。從另一個角度回答了“為什么平行四邊形面積不能表達為相鄰兩邊長度的乘積”。

三、關聯的眼光

有了上面的認識，接下來的問題是：如何看出等底等高平行四邊形與長方形面積之間的關系？教科書中通常的方法是，通過剪拼和移補，將平行四邊形等積變換為長方形。下面介紹另外一個方法。圖4中兩條平行線L1和L2之間，ABCD為長方形，EFGH為平行四邊形，二者等高且DC=HG。

這個梯形原本沒有，是人為識別出來添加到問題情境中的，這樣的思維方式通常叫作“轉換推理（Transformational Reasoning）”。如果將長方形ABCD與這個梯形合并為一個圖形看，就可以得到一個更大的梯形AEHD（見圖6）。

同樣可以將梯形BEHC與右側平行四邊形EFGH合并，得到另外一個更大的梯形BFGC（見圖7）。

對比兩個梯形AEHD和BFGC，不難看出二者形狀和面積大小都是一樣的。而中間梯形BEHC是二者公共部分，依據“等量減等量仍相等”，就可以看出長方形ABCD和平行四邊形EFGH面積相等。

事實上，長方形和平行四邊形面積是否相等，并不是由邊的長短決定的，而是由相同位值橫截出來“寬度”（圖8中用字母a表示），以及高度（圖8中平行線L1和L2之間的垂直距離）決定的。

運用這樣的轉換推理，還可以得到更一般的結論。事實上，任意兩個圖形只要符合高度和寬度相等的條件，其面積都是相等的（見圖9）。

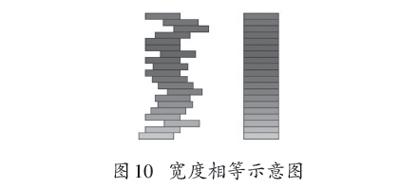
圖9中ABCD是一個長方形，EFGH是一個曲邊圖形，由于二者高度和寬度相等，那么長方形ABCD與曲邊圖形EFGH面積相等。這樣的事實，可以從圖10直觀地看出來。

相同數量的小長方形分別擺放為圖10形狀，雖然擺放方式不同，由于相同位值的寬度以及高度相等，那么二者的總面積一定相等。同樣道理，圖11中三個曲邊圖形面積也是相等的。

直觀地看，整個圖形面積就是所有寬度“c”積累出來的，由于對應位置的寬度都相同，自然積累出來的總面積也應當相同。

四、直觀感知微積分

這樣的事實，是意大利數學家卡瓦列里（Franeesco Bonaventura Cavalieri，1598-1647）最早發現的，后人稱之為“卡瓦列里原理（Cavalieris Principle）”，也可以認為是“微積分”在幾何中的直觀表達。

牛頓（Isaac Newton，1643-1727）發明的微積分早期叫作“流數法”。其中“流數（Fluxion）”和“流量（Fluent）”是兩個核心概念。前者相當于運動的速度，后者相當于運動的距離。比如一個長方形ABCD，按照“線動成面”的眼光看，可以把這個長方形看成是一條運動線段EF沿著垂直于它的方向從AB位置運動到CD位置所留下的軌跡（見圖12）。

圖12中運動線段EF的長度a就是這個運動過程中的流數，掃過長方形ABFE的面積ax是這個運動過程中的流量，其中的x相當于運動過程中的時間變量。當線段EF運動到CD位置時，流量ax就成為長方形ABCD的面積了1。

圖11中，寬度c相當于流數，高度h與寬度c的乘積相當于流量。整個圖形面積被看作是所有位置的寬度c積累出來的。

論及流數法的基本原理，牛頓在其名著《流數法與無窮級數》的前言中說：“可以把數學中的量看作是連續的局部運動產生出來的。”[1]在幾何形體的求積（Quadrature）問題中，“數學中的量”就是描述長短、大小的長度、面積和體積。牛頓這種運動的眼光實質上是改變了歐幾里得《幾何原本》中“積點成線，積線成面，積面成體”的看法，把幾何形體看成為“點動成線，線動成面，面動成體”。因此可以說，小學數學中關于長度、面積、體積的內容中，實際蘊含著牛頓流數法中“運動”和“積累”的思想，應當成為讓學生感悟的內容。

綜上，貌似容易的“平行四邊形面積”的學習，不僅是公式的推導和應用，還應當讓學生經歷與已有經驗中的長方形進行比較的過程。在經歷這樣的過程中，學生有機會體驗用透視的眼光、關聯的眼光和運動的眼光看待事物。

參考文獻：

[1] Isaac Newton. The Method of Fluxions and Infinite Series[M]. LONTON. Printed by Henry Woodfall. M.DCC.XXXVI. pxi.

（首都師范大學初等教育學院? ?100048）