想象先行 虛實相融
——《圖形的運動（三）》教學實踐（一）

方愛英

【教學內容】

人教版五年級下冊第83、84頁。

【教學過程】

一、創設情境，引出研究問題

師：請兩位同學上來和老師完成一個小游戲，再請其他同學邊觀察邊思考：你觀察到了哪些運動現象？（學生聽口令做動作：“齊步走、向右轉、向左轉、向后轉”等）

生：“齊步走”是平移，“向右轉、向左轉、向后轉”是旋轉。

師：我們在二年級時已經初步認識過生活中的平移和旋轉現象，今天進一步來學習圖形的旋轉。（板書課題：圖形的旋轉）

二、展開探索，認識旋轉要素

1.觀察比較，掌握旋轉方向。

師：能舉幾個旋轉的例子嗎？

師：老師也收集了一些生活中的運動現象，你能從中發現旋轉運動嗎？它們是怎么旋轉的？（出示鐘面、風車、道閘、秋千）

生：我認為鐘面上的指針和風車上的葉片是旋轉運動。

師：（動態展示鐘面上指針和風車葉片旋轉的過程）同樣是旋轉，它們有什么不一樣的地方？

生：它們旋轉的方向相反。

師：像這樣，順著鐘面上指針旋轉的方向叫順時針方向，和它相反的方向如風車葉片剛才旋轉的方向叫逆時針方向。（板書）

師：請同學們將自己的右臂想象成時針，按照指令做運動：

（1）手臂指向12 時位置，順時針旋轉90 度，逆時針旋轉90 度；

（2）手臂指向9 時位置，順時針旋轉90 度，逆時針旋轉90 度。

生：我認為這兩次運動不是旋轉，因為它們沒有旋轉一圈。

生：我認為是旋轉，只要它轉動了就是旋轉，沒有規定它一定要轉一圈。

師：同學們的爭論很有價值，是不是一定要轉一圈才算旋轉？接下來我們繼續從數學的角度研究圖形旋轉到底有哪些特征。

2.借助鐘面，明確其他的兩個要素。

（1）認識旋轉中心。

動態展示甲鐘面指針從“12”旋轉到“1”，乙鐘面指針從“2”旋轉到“5”。

師：甲乙兩個鐘面上指針旋轉的過程有什么相同？

生：方向相同。都是順時針旋轉的。且指針旋轉過程中都是只有一端動，另一端不動。

師：指針圍繞一個中心點旋轉，這個中心點叫旋轉中心。（板書）

生：我發現旋轉中心是不動的，旋轉中心在哪兒，旋轉運動就發生在哪兒。

（2）認識旋轉角度。

師：甲乙兩個鐘面上指針旋轉過程有什么不同？

生：指針的起止位置不一樣，旋轉的角度不一樣。（板書）

師：你能借助鐘面判斷它們分別旋轉了多少度嗎？

生：甲鐘面的指針旋轉了30度。因為周角是360 度，鐘面上有12 大格，平均分成了12 份，一份就是30 度。

生：乙從“2”走到“5”，旋轉了3 大格，所以是90 度。旋轉幾大格，就是幾個30 度。

（3）描述旋轉過程。

師：想象一下，指針是如何從“12”旋轉到“1”的？

生：指針繞點O，從“12”起順時針方向，旋轉30 度到“1”。

師：通過學習，你知道描述旋轉運動必須具備哪些要素嗎？

生：描述旋轉運動必須具備旋轉中心、旋轉方向、旋轉角度三個要素。

3.借助想象，深入理解旋轉要素。

（1）想象旋轉過程。

師：（出示一個空白鐘面）指針從“6”到“9”，你能想象出旋轉過程嗎？

生：指針從“6”起，繞點O 順時針方向，旋轉90 度到“9”。

師：只能這樣旋轉嗎？

生：指針從“6”起，繞點O 逆時針方向，旋轉270 度到“9”。

（2）深入理解旋轉。

師：（取出自制鐘擺教具展示運動，并用粉筆把鐘擺運動的軌跡留下）這是旋轉運動嗎？

生：是的。圍繞一個點進行旋轉，既包含了順時針旋轉，也包含了逆時針旋轉，只不過沒有旋轉360 度。

師：（出示道閘和秋千圖）現在，你能明確判斷它們是不是旋轉運動嗎？

生：肯定是的。

師：（出示道閘運動動態圖）說說車輛進小區和出小區時，道閘是如何旋轉運動的？

生：車輛進小區時，道閘繞點O 逆時針旋轉90 度；出小區時，道閘繞點O 順時針旋轉90 度。

三、動手操作，感悟旋轉實質

1.線段的旋轉。

師：如果把指針看作一條線段，用OA 來表示，想想看，線段能旋轉嗎？可以怎么旋轉？拿出一支筆，用它來表示線段OA，在練習紙的方格中感受一下可以怎么旋轉？

生：可以繞點O，也可以繞點A；可以順時針旋轉，也可以逆時針旋轉。

師：想象一下，線段OA 如果繞點A 逆時針旋轉90 度會旋轉到什么位置？把它畫在方格紙中。

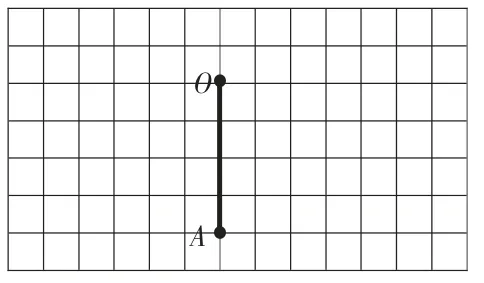
師：誰愿意介紹一下自己是怎么畫的？觀察旋轉前后的線段，什么變了？什么不變？

生：旋轉后的線段，形狀、大小沒變，位置變了。

師：這里還有幾份畫的不太一樣的，我們一起來看看，有什么問題？

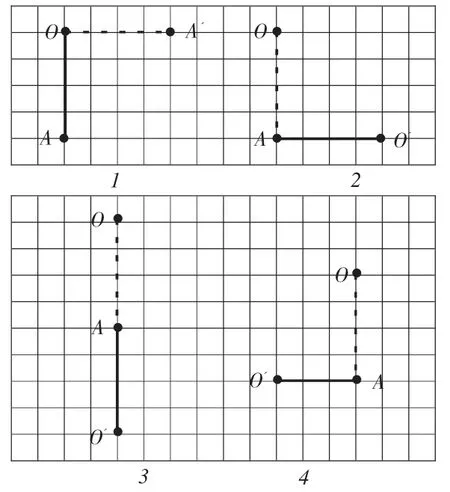
生：1 號是旋轉中心錯；2 號是旋轉方向錯；3 號是旋轉角度錯；4 號是線段長度錯。

師：看來在畫圖的時候一定要注意旋轉的中心、方向和角度三個要素，并注意旋轉前后形狀、大小不變。

2.三角形的旋轉。

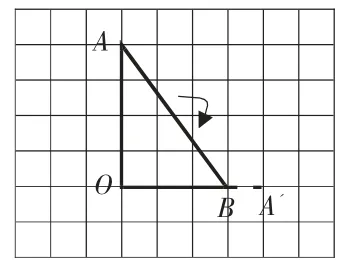
師：三角形AOB 繞點O 順時針旋轉90 度后，想象一下，得到的會是什么樣的圖形呢？用老師提供的活動三角形學具，在方格紙上操作。

師：你發現了什么？

生：和線段旋轉一樣，形狀大小沒變，位置變了。

師：如何確定三角形旋轉后的位置？

生：我發現和前面線段的旋轉是一樣的，以O 為旋轉中心，確定了線段AO、BO 旋轉后的位置，也就確定了整個三角形旋轉后的位置。

生：他的意思也就是三角形的每條直角邊都繞點O 順時針旋轉90 度。

師：如果繼續繞點O 順時針旋轉90 度，兩次旋轉后的圖形，會組成一個什么圖案？

（學生回答后，動態演示風車形狀形成的過程）

3.借助補白，深入感悟。

課件出示練習：

（1）怎樣旋轉90°，A 點與A1重合？

（2）怎樣旋轉90°，A 點與A2重合？

（3）怎樣旋轉90°，A 點與A3重合？

（4）怎樣旋轉90°，A 點與A4重合？

生：三角形ABC 繞點C 逆時針旋轉90°，A 點與A1重合。

生：三角形ABC 繞點C 順時針旋轉90°，A 點與A2重合。

生：三角形ABC 繞點B 順時針旋轉90°，A 點與A3重合。

生：三角形ABC 繞點B 逆時針旋轉90°，A 點與A4重合。

師：你們是如何確定的？

生：我是根據邊的旋轉確定的。因為AC 繞點C 逆時針旋轉90°后與A1C 重合，所形成的夾角是90°。

生：AC 繞點C 順時針旋轉90°后與A2C 重合，所形成的夾角是90°。

生：BC 繞點B 順時針旋轉90°后與BC′重合，所形成的夾角是90°。

生：BC 繞點B 逆時針旋轉90°后與BC″重合，所形成的夾角是90°。

師：（課件演示驗證）通過剛才的學習，你能發現如何判斷圖形的旋轉是否正確嗎？

生：我發現可以把圖形的旋轉轉化為邊的旋轉，特別是與旋轉中心相連接的邊。

師：這位同學的回答很重要，把圖形的旋轉轉化為邊的旋轉，也就是線段的旋轉，看似復雜的圖形旋轉就會變得非常簡單。誰還補充？

生：通過邊的旋轉來判斷圖形的旋轉是否正確時，最好選擇與格線重合的邊，比較容易判斷旋轉角度和旋轉后邊的長短是否變化。

師：是的。這一點也非常重要。

四、欣賞圖案，感受旋轉應用

欣賞生活中，尤其是美術中，利用旋轉生成的若干美麗圖案。