巧用表格，探尋應用題中的等量關系

龐秀軍

【摘? 要】表格中可以列出有關數據、符號、公式、表達式或文字等需要說明的事項，它能夠反映出較復雜問題中的數量關系，通過分析這些數量關系就可以探尋出應用題中的等量關系，從而列出方程。在列表格時，要求學生表格中的內容既要完整，又要全面。

【關鍵詞】表格;應用題;學生;等量關系

列方程（組）解應用題是通過建立方程模型解決實際問題，是方程（組）的實際應用。探尋出題目中各數據的數量關系，從而找到等量關系，是列方程（組）解應用題的關鍵，但這也是學生學習時的難點。我通過近三十年的教學經驗發現，巧用表格，可以使學生很容易探尋出應用題中的等量關系。由于在表格中可以列出有關數據、符號、公式、表達式或文字等需要說明的事項，它能夠反映較為復雜問題中的數量關系，通過分析這些數量的關系就可以探尋出應用題中的等量關系。可以說巧用表格，探尋應用題中的等量關系伴隨著學生整個初中階段的學習。下面舉幾例說明。

例1：一家商店將某種服裝按成本價提高40%后標價，又以8折優惠賣出，結果每件仍獲利15元，這種服裝每件的成本是多少元？（北師大版七年級數學上冊第115頁引例）

學生剛看到這個題目時，都能完成第一步：設這種服裝每件的成本是x元。但對如何找出題目中的等量關系和列出方程卻感到非常困難。因此，我鼓勵他們可以先畫出表格，將題目中的數據例在表格中。他們通過個人的努力和小組合作，畫出并填充出如下表格：

通過分析表格中各數據之間的關系，自然得出了本題的等量關系：售價-進價=已知的利潤15元，進而列出了如下的方程并完成了整個解題過程。

（1+40%）·80%-x=15

在隨后學習“希望工程義演”“等積變形”等內容時，我也鼓勵學生利用表格尋找等量關系，列出方程。

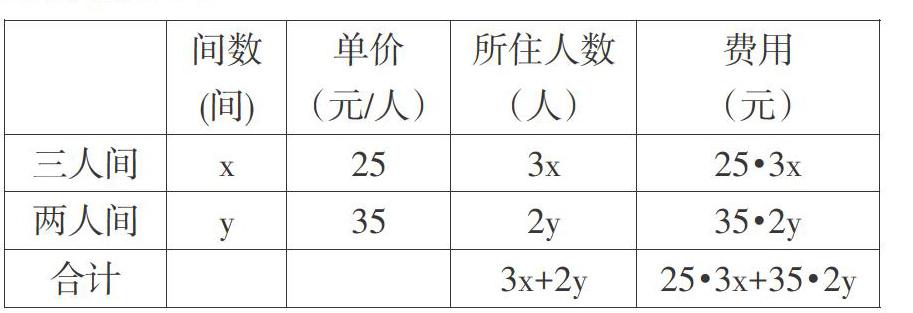
例2：某旅館的客房有三人間和兩人間兩種，三人間每人每天25元，兩人間每人每天35元。一個50人的旅游團到該旅館住宿，租住了若干客房，且每個客房正好住滿，一天共花去住宿費1510元。兩種客房各租住了多少間？（北師大版八年級數學上冊第119頁第2題）

本題要求兩個未知量，即兩種客房分別租住的間數。為此，學生設出了如下兩個未知數：三人間租住了x間，兩人間租住了y間。為了尋找各數據之間的數量關系以及本題的等量關系，我要求學生采用表格的方式。在列表格時，要求他們表格中的內容既要完整，又要全面。在學生的共同努力下，他們圓滿地完成了列表的任務，并進行了填充。他們完成的表格如下：

學生通過審題并根據填充的表格，發現題目中有兩個等量關系：

（1）兩種房間所住人數之和=50人

（2）兩種房間所需費用之和=1510元

所以根據等量關系列出了如下的方程組：

3x+2y=50? ? ? ? ?①

25·3x+35·2y=1510? ②

由于正確地列出了方程組，所以我的學生很快完成了本題的完整解答。

在八年級學習“ 雞兔同籠 ”“增收節支 ”等應用題時，我都要求學生運用表格探尋題目中各數據之間的數量關系，從而發現等量關系、列出方程、完成解題。

一元二次方程的利潤問題是中考的常考題型，它與二次函數中的最大利潤問題聯系比較密切，可以說，一元二次方程的利潤問題掌握了，二次函數中的類似問題也就能夠輕松解決。所以，在學習一元二次方程的利潤問題時，我要求學生必須全部掌握。但是這類問題數據較多，數量關系較為復雜，所以學生有時理不清各數據之間的關系，因而也就很難發現題目中的等量關系，更不用說列出方程，完成求解。在此，我還是要求他們從表格入手，將關鍵數據在表格中表示，讓他們去發現，去探尋。

例3：新華商場銷售某種冰箱，每臺進貨價為2500元。調查發現，當銷售價為2900元時，平均能售出8臺;而當銷售價每降價50元時，平均每天多售出4臺。商場要想使這種冰箱的銷售利潤平均每天達到5000元，每臺冰箱的定價應為多少元？（北師大版數學課本九年級上冊第54頁例2）

本題是九年級的一道應用題，大部分學生都知道本題既可以直接設未知數，也可以間接設未知數。為了計算的簡便，我先要求學生利用間接設法，即：設每臺冰箱降價x元。但是對接下來如何探尋題目中各數據間的關系，如何找到等量關系、列出方程，學生就感到非常困難，覺得無從下手了。此時，我提示道：在初一學習打折銷售時，我們借助表格，去探尋題目中各數據之間的數量關系，你們能不能也試著列出表格，但是先不要填充內容，只是表明表格中每一行和每一列所代表的實際意義。接著我讓學生先獨立完成，然后進行小組合作，最后再在班里分享各小組的結果。經過他們的共同努力，畫出了如下表格：

解：設每臺冰箱降價x元

通過讀題，學生已經知道：每臺的利潤[×]銷量=總利潤，所以依此為等量關系，就列出了如下方程：

（2900-x-2500）（ ）=5000

由于列出了方程，后面的解題過程就變得容易了。因為本題也可以通過直接設未知數的方法列出方程，所以接著我又讓學生按照直接設法，重新填充以上表格，并讓學生自己去發現在表格中所填充的內容有哪些發生了變化，為什么會有這樣的變化，通過這種比較可以使學生鞏固所學的知識。學生根據表格中各數據之間的數量關系和題目中的等量關系列出了新的方程，并完成了整個求解過程。

當然，分析問題、解決問題的方法多種多樣，巧列表格，探尋應用題中的等量關系只是其中的一種。所以，在教學中我們也要鼓勵學生一題多解或多題一解，這樣可以培養學生的思維，提高解題的靈活性。

參考文獻：

[1]張曉鵬.等量關系覓尋：初中數學方程應用題解題的核心線索[J].數學教學通訊，2014（4）.

[2]楊沙九.解決初中應用題中列方程的思考方法[J].數學學習與研究，2014（8）.

[3]蔣寶慧.用列表格法找出應用題中的等量關系[J].中學生數學，2009（2）.

（責任編輯? 袁 霜）