新五模類Lorenz系統的動力學行為分析及仿真

王賀元, 李 佳, 王美玉, 宋斯琦, 王曉帆, 曹婷婷

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

0 引 言

刻畫流體運動的Navier-Stokes方程是經典的非線性偏微分方程,研究其解的性態有助于認識湍流的生成機理。探討其解的穩定性及分岔問題是近些年人們普遍關注的焦點,吸引眾多學者對其進行了廣泛的研究。自混沌之父Lorenz[9]給出著名的Lorenz系統以來,采用降維方法討論無窮維動力系統方面的工作層出不窮[1-8]。Valter Francechini科研團隊將如下的Navier-Stokes方程

其中:u為速度場;f為外力;p為流體壓強;ν為動力粘性系數。

在平面規則區域上進行有限維約化,獲得了一些有限維的動力系統[1-4]。基于二維區域上的這種約化方法,Franceschini等[7]討論了三維區域上的Navier-Stokes方程,獲得了空間區域上的五模系統,后來又陸續得到了七模、十四模等有限維動力系統,并且探討了這些有限維系統復雜的動力學性態[3]。

本文將約化二維區域上不可壓縮Navier-Stokes方程,獲得新五維類Lorenz系統,探討系統吸引子的存在性,并進行全局穩定性分析,對系統動力學行為進行數值仿真。

1 Navier-Stokes方程的約化及類Lorenz系統的穩定性

對平面區域[0,2π]×[0,2π]上Navier-Stokes方程進行有限維約化,把速度場u,外力f,壓強p展開為如下傅氏級數:

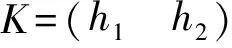
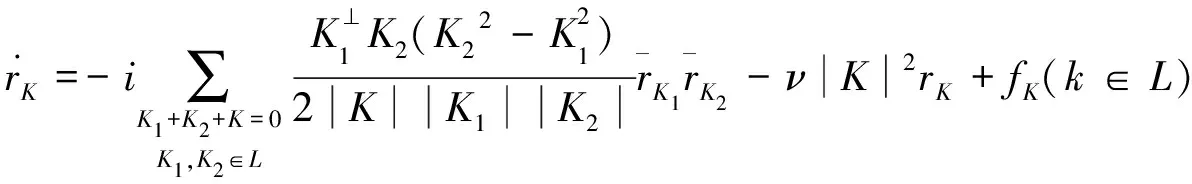
其中:ν為動力黏度系數;L為波向量集合,并且有若K∈L則-K∈L。

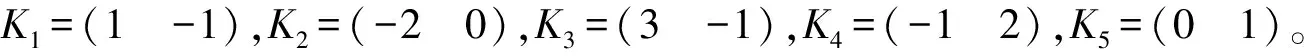
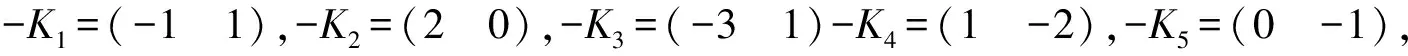
在ν=1時分別令K為K1,K2,K3,K4,K5,代入到方程組(7)經大量計算,得到如下方程組:

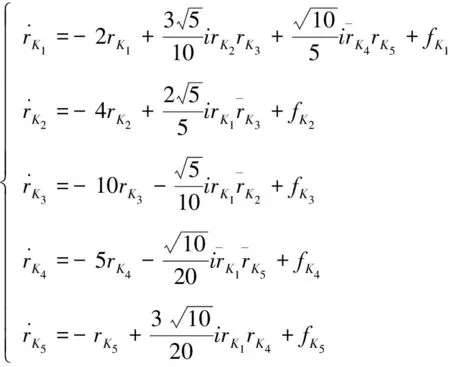
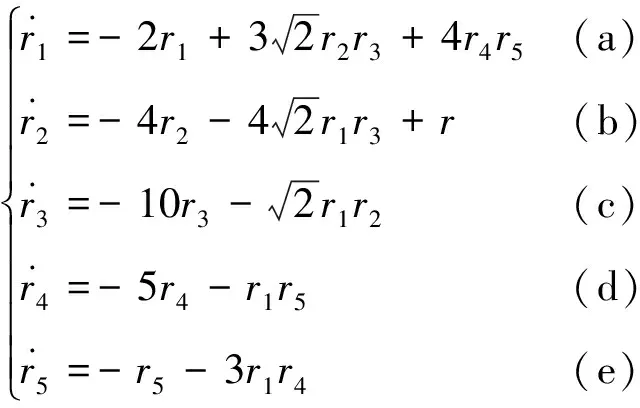
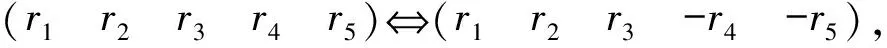
基于奇點鄰域內的線性穩定性分析可以討論非線性系統解的性態,這就是Liapunov第一方法[5]。Liapunov矩陣的特征指數是指Jacobi矩陣特征值的實部,它能較好地刻畫吸引子的性質。基于奇點的Liapunov矩陣的特征指數可以分析和討論奇點的穩定性。

令

對F(X,r)求導數得到

由F(X,r)=0求出奇點,依據Liapunov矩陣的特征指數符號判別各奇點的穩定性:

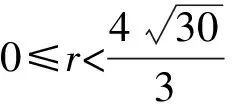
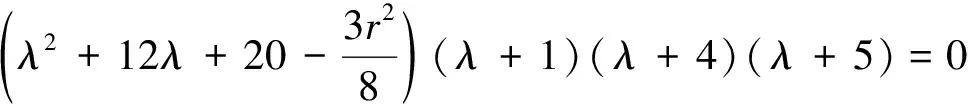
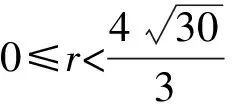
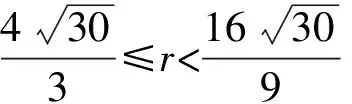
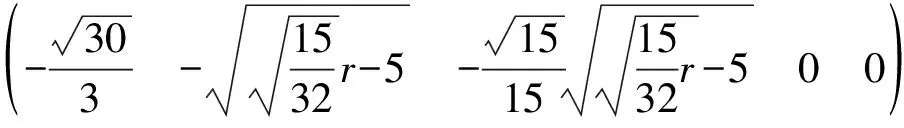
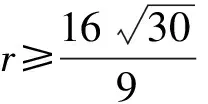
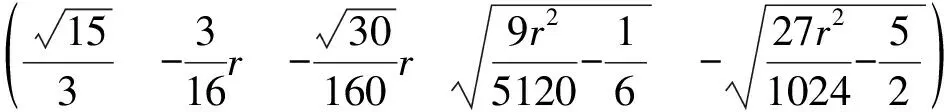
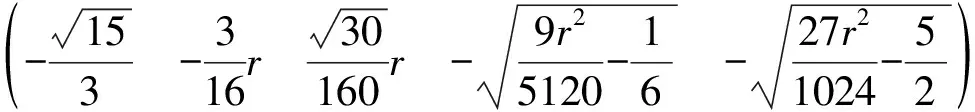
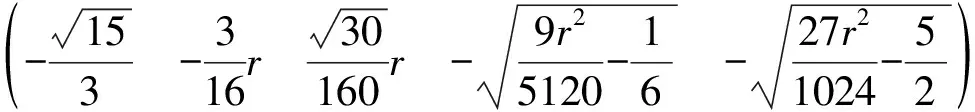
對于奇點(1)(2)(3),由于Jacobi矩陣特征值的變化而失去穩定性,奇點(4)(5)(6)(7)在r<9.737…的范圍內始終是穩定的。

2 吸引子的存在性

非線性方程解的性態是極其復雜的,一般無法通過簡單的推導和運算來獲得。近年來,基于Sniale等的思想[8],耗散系統的混沌行為是由于存在混沌吸引子引起的,而混沌吸引子是系統所有軌道的長時間行為。混沌吸引子的復雜結構是導致系統出現混沌現象的原因。所以,探討吸引子的存在性就顯得尤為重要。下面討論系統(9)吸引子的存在性。

對系統(9)進行運算

(a)×r1+(b)×r2+(c)×r3+(d)×r4+(e)×r5得:

因此有

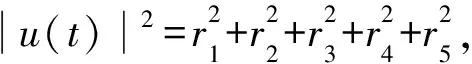
取ε=2,得

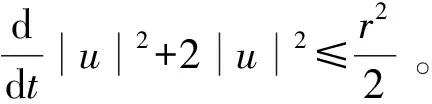
因此有

故有

當ρ充分大時,B(0,ρ)是吸引集和泛函不變集,因此存在全局吸引子。

3 全局穩定性

如果具有全局穩定性,系統的軌線所收斂的單連通閉區域稱為系統的捕捉區。如果能證明捕捉區存在,也就表明無論奇點是否穩定,系統永遠是全局穩定的。基于Liapunov第二方法[5],構造V函數討論系統(9)的穩定性。

對系統(9)構造Liapunov函數:

令V(r1,r2,r3,r4,r5)=K,很明顯,當K是一正常數時,上式表示一球面,記為E。

求V的導數:

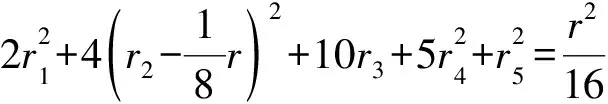
由式(14)可知:

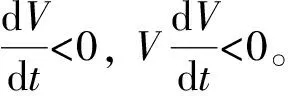
4 數值仿真

隨參數r的變化,系統(9)的穩定性將發生改變, 將出現分叉和混沌等現象。如下圖形均取x1,x2,x5這3個分量,其他分量可類似討論.

1) 當r<8.3…時,軌道是穩定的螺旋線,環繞一點進行旋轉,并且螺旋線越來越密集,最后變成極限環;當r>9.49…時,極限環失穩,分岔出新軌線,與原軌線形狀相似,且與原軌線形成交叉環(圖4)。這種現象和文獻[1]中的r=28.6時是類似的。這種雙軌道的情況不會立即消失,在r某一變化范圍內存在。

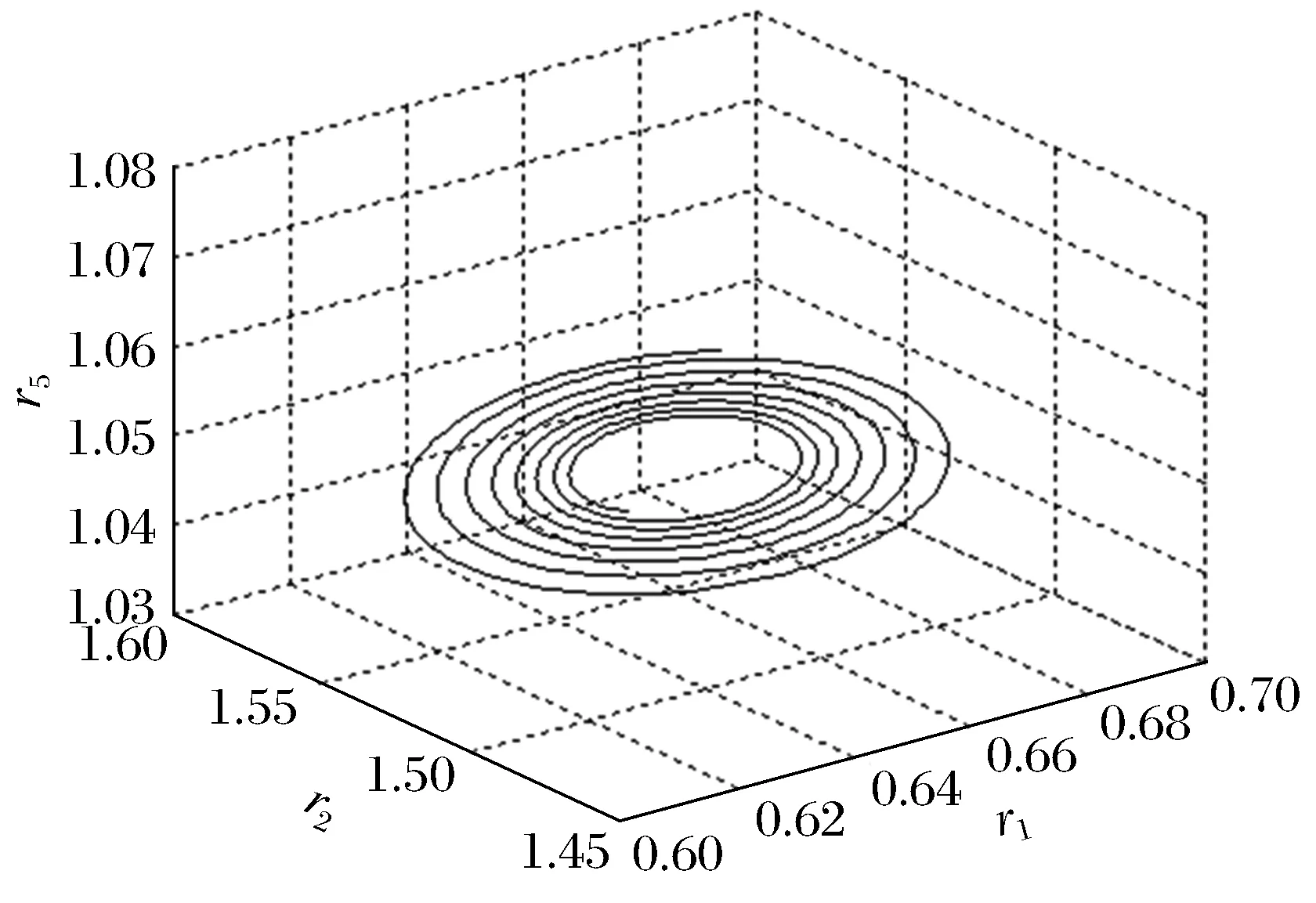
圖1 (r=8.1)螺旋線Fig.1 (r=8.1)spiral

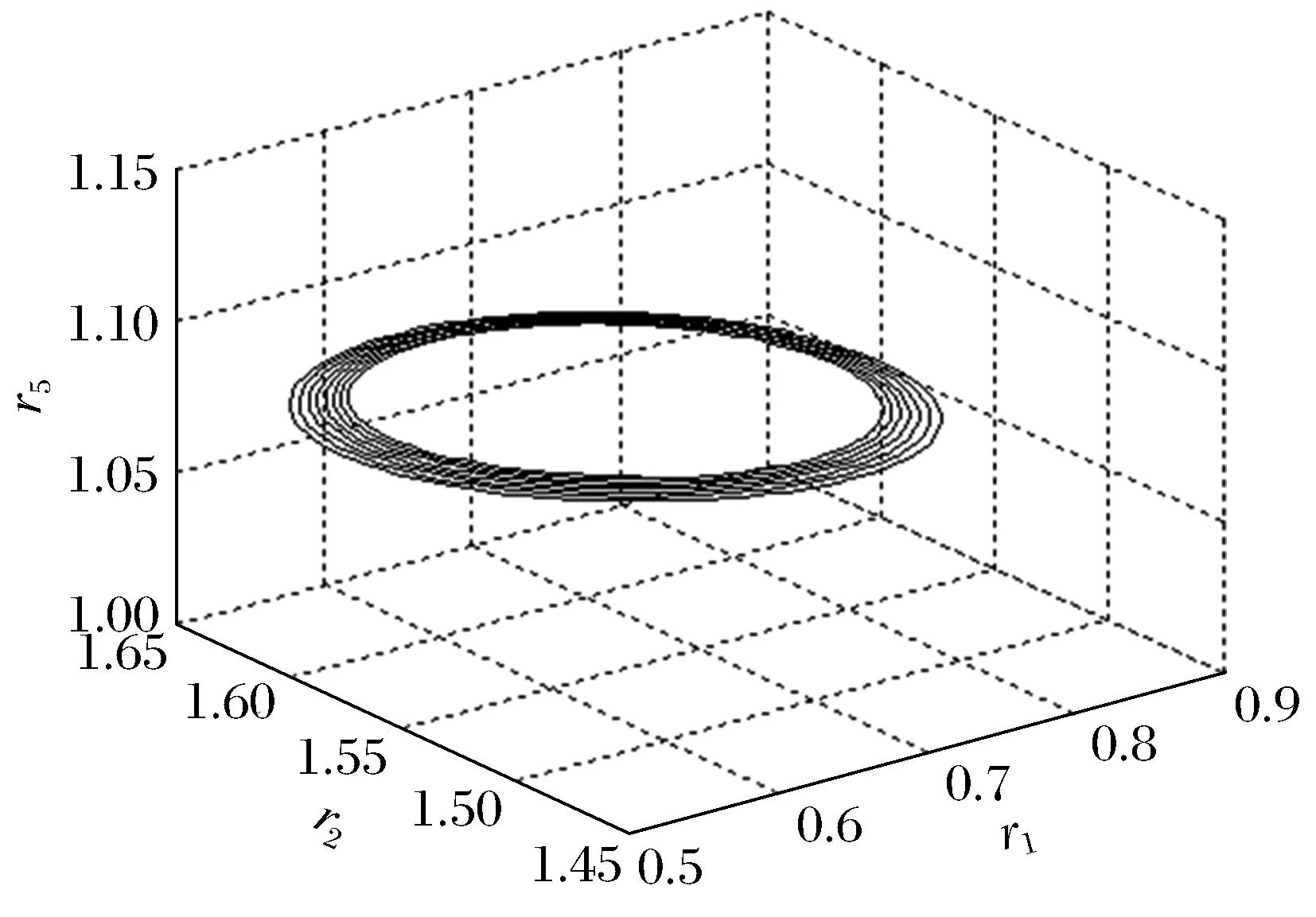
圖2 (r=8.3)收縮的螺旋線Fig.2 (r=8.3)contractile spiral

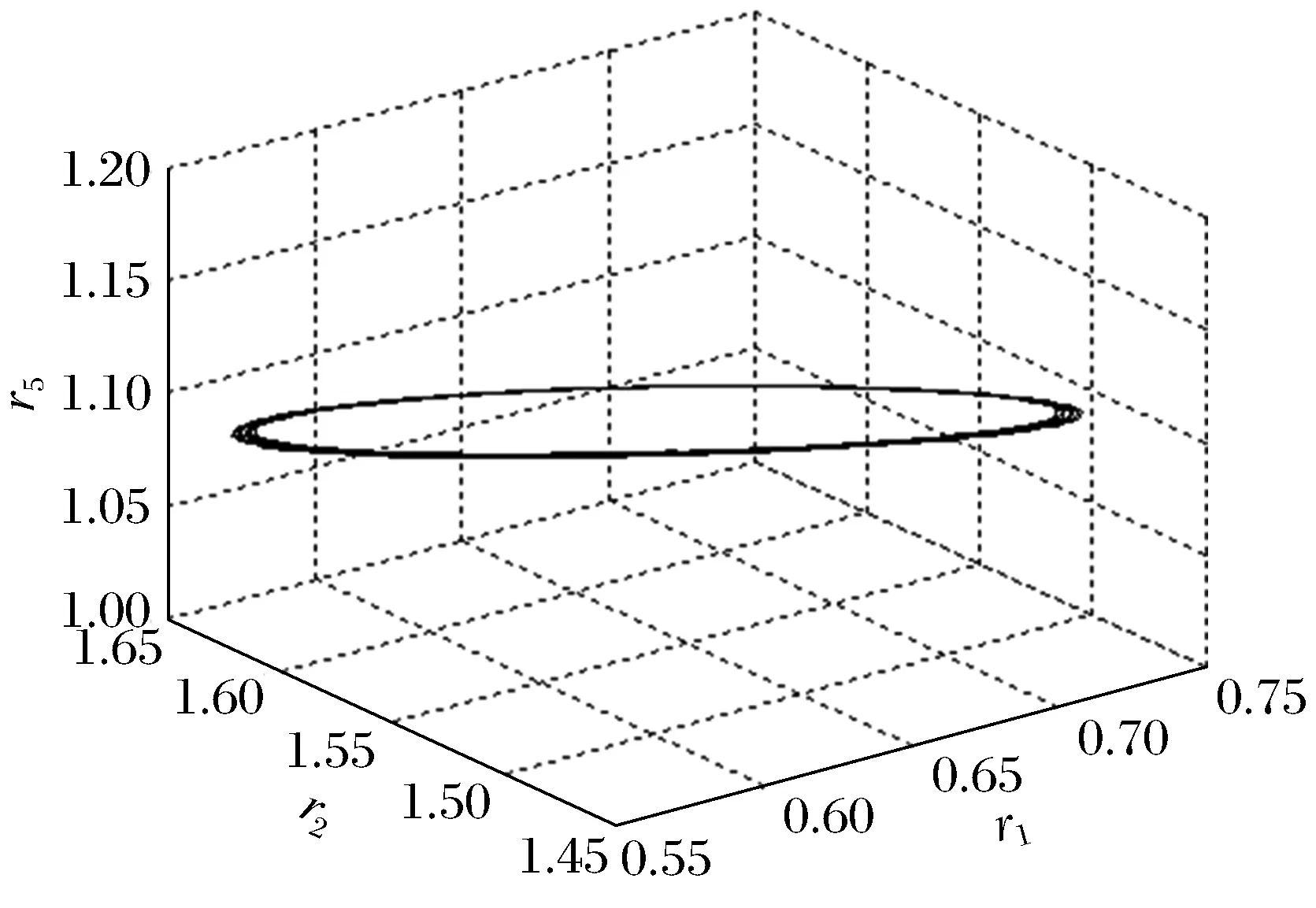
圖3 (r=8.34)極限環Fig.3 (r=8.34)limit cycle

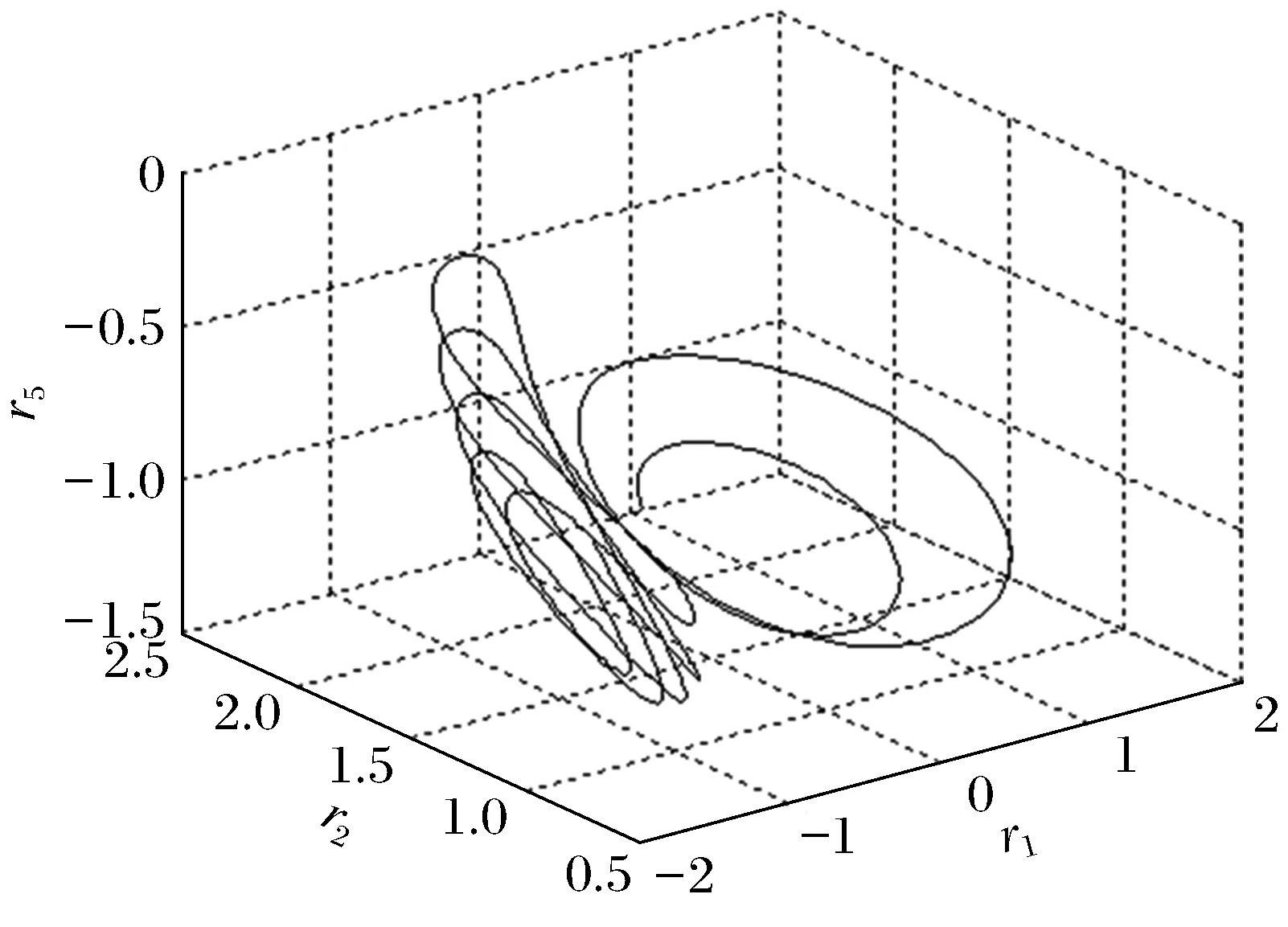
圖4 (r=9.49)雙螺旋軌道Fig.4 (r=9.49)double helix orbit

2) 當r=9.52…時,環形軌線出現新分支,環繞另一奇點旋轉(圖5)。從這以后環形軌線繞2個奇點來回環繞,產生奇怪吸引子。圖6、圖7、圖8刻畫了不同參數下奇怪吸引子的形態。

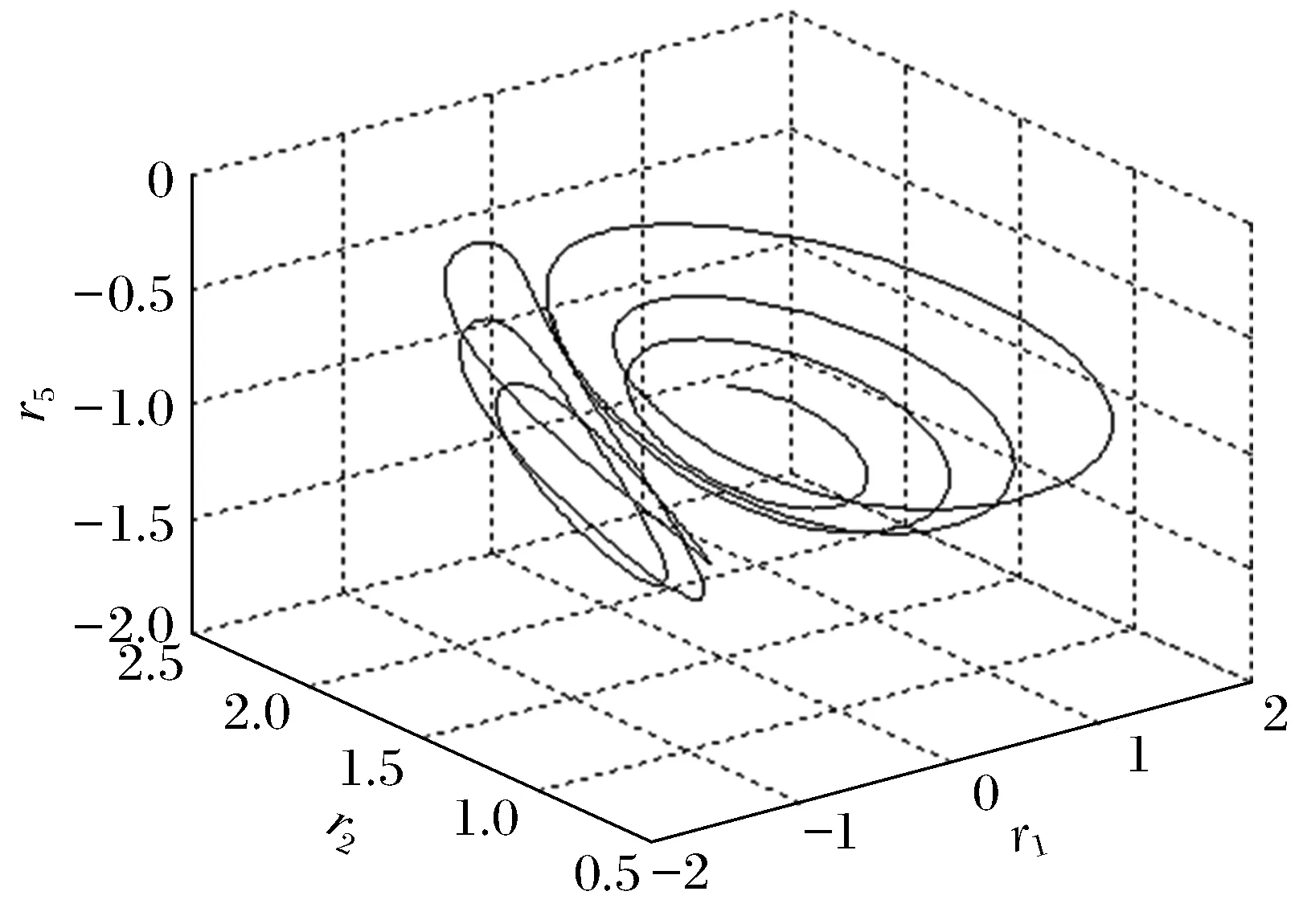
圖5 (r=9.52)雙螺旋軌道Fig.5 (r=9.52)double helix orbit

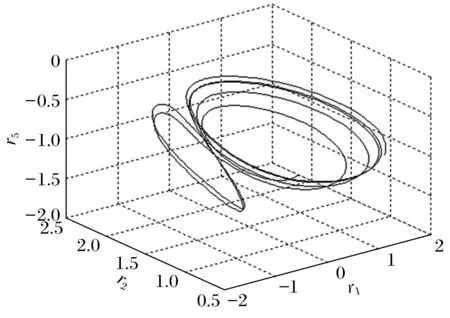
圖6 (r=9.737)奇怪吸引子Fig.6 (r=9.737)strange atractor

圖7 (r=9.809)奇怪吸引子Fig.7 (r=9.809)strange atractor

圖8 (r=9.85)過渡軌線Fig.8 (r=9.85)transition trajectory

3) 當r=9.9…時,奇怪吸引子變為2個交叉極限環(圖9和圖10),以后保持這種狀態很長一端時間,然后軌線逐漸演變為環面(圖11和圖12)。

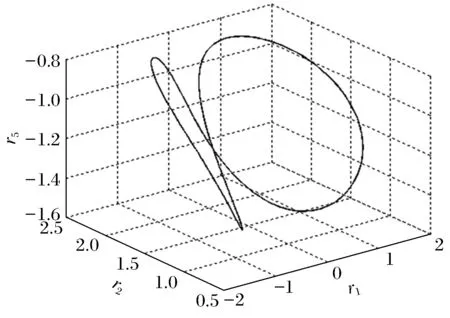
圖9 (r=9.9)極限環Fig.9 (r=9.9)limit cycle

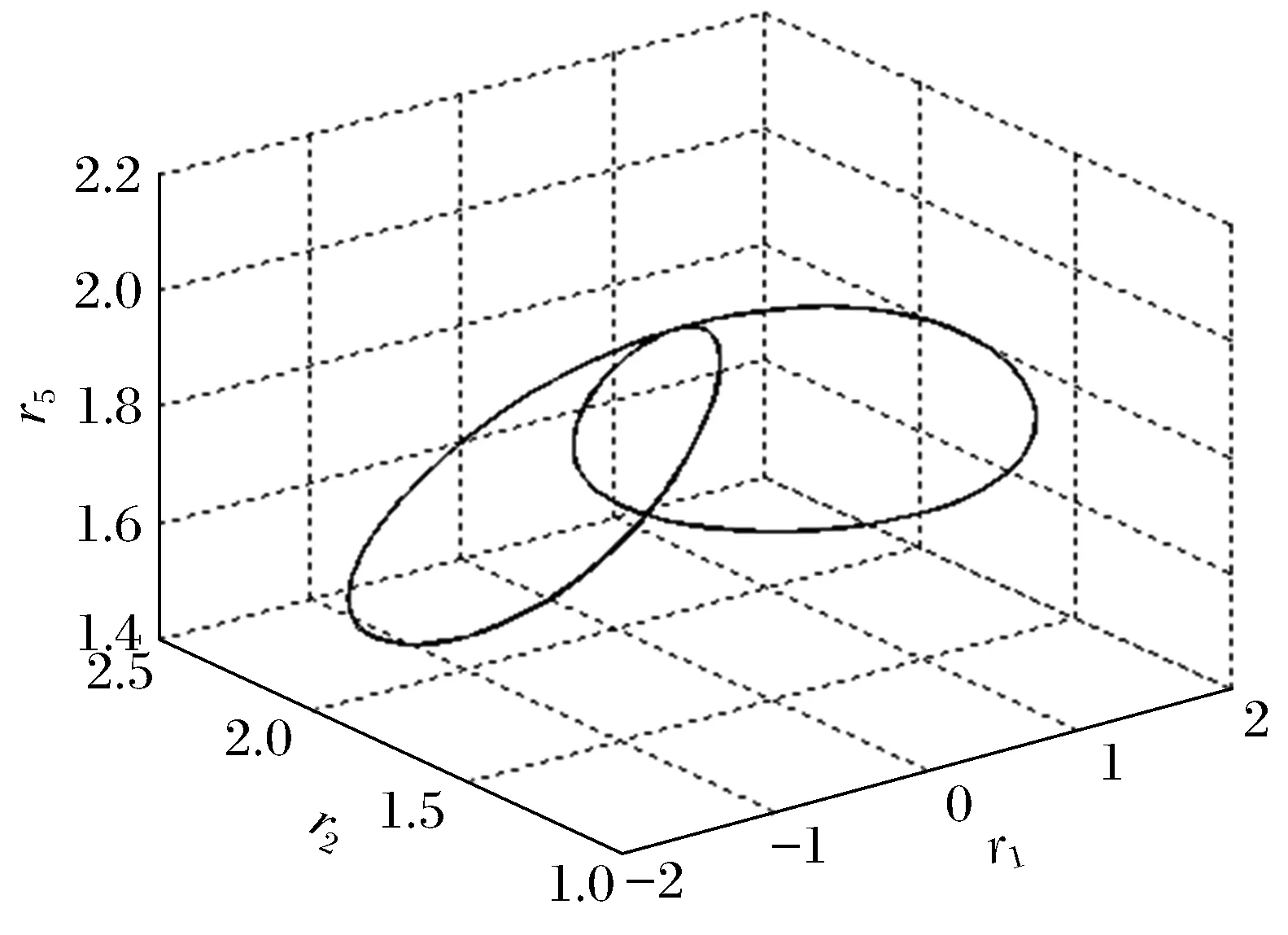
圖10 (r=12)極限環Fig.10 (r=12)limit cycle

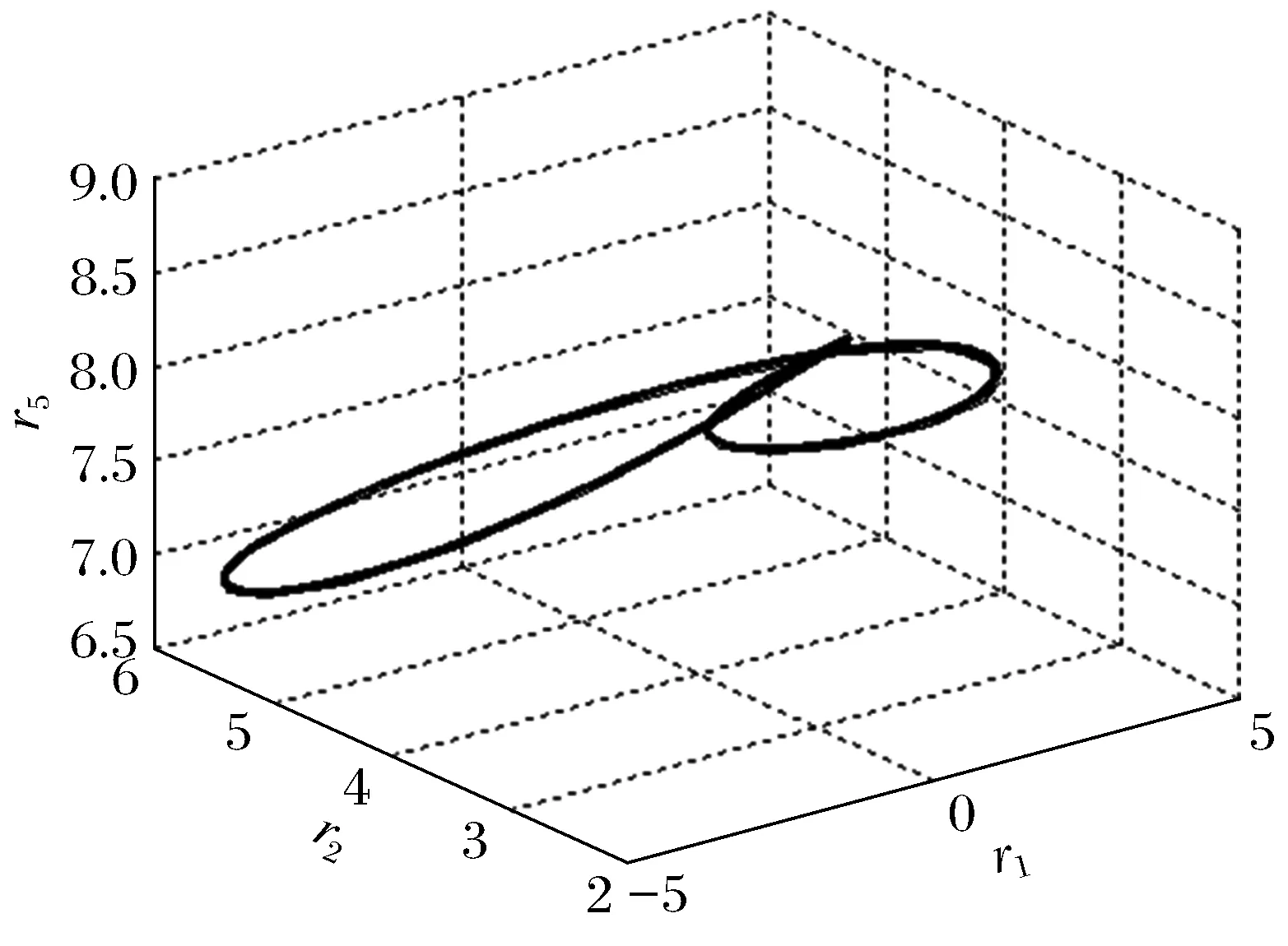
圖11 (r=49)環面Fig.11 (r=49)torus

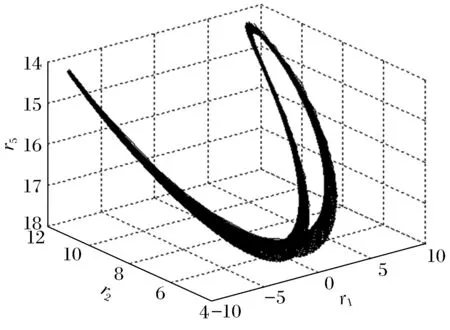
圖12 (r=105)環面Fig.12 (r=105)torus

以上的仿真分析也進一步證實了混沌運動是確定性和隨機性的對立統一,表明了它對初始狀態的敏感依賴性。以上是無窮維系統有限維約化的一個簡單例子,有興趣的讀者可進一步參考有關文獻[11-15]。

5 結 論

本文對平面正方形區域上不可壓縮Navier-Stokes方程進行有限維約化,得到新五維類Lorenz系統,通過穩定性分析和數值仿真,揭示了系統解的動力學行為。新約化模式及系統混沌行為的仿真具有一定的實際意義。