淺談如何在高等數(shù)學中融入思政教育

翟麗麗　羅東風　章樹玲　董艷　羅寧　白梅花　趙馨

摘? 要：在學生的教育中加入思政元素是對當今教育改革的積極探索。而高等數(shù)學課程在與思政想結(jié)合的過程中具有天然優(yōu)勢，思政中含有豐富的思政教育資源，高等數(shù)學的有些問題本身就蘊含了深刻的哲學思想。本文以定積分概念的講授為例，在引入概念時分析了定積分的定義產(chǎn)生的過程中所蘊含的數(shù)學思想和哲學思想，并且在高等數(shù)學授課中通過適當融入數(shù)學在實際生活中的應(yīng)用問題，做到了激發(fā)學生的學習積極性，并解決了將高等數(shù)學與思想教育相結(jié)合的問題。

關(guān)鍵詞：高等數(shù)學? 定積分? 思政教育

中圖分類號：G642 ? ?文獻標識碼：A 文章編號：1672-3791（2020）04（c）-0234-02

《高等數(shù)學》含有豐富的思政教育資源：在學習的過程中，可以介紹相關(guān)人物以及歷史背景，激發(fā)學生對課程的學習興趣，降低學生對數(shù)學的畏難情緒;可以對數(shù)學史的發(fā)展進行介紹，讓學生掌握數(shù)學發(fā)展的規(guī)律，體會數(shù)學家求真務(wù)實的態(tài)度，從而提高學習積極性;還可以適當引入數(shù)學悖論，讓學生認清問題的本質(zhì)，激發(fā)學習的興趣;也可以適當講解數(shù)學在實際生活中的應(yīng)用，這樣就避免課程因理論性強、內(nèi)容多、知識點難而學起來枯燥。

下面以定積分概念的講述為例，在高等數(shù)學的授課過程中結(jié)合實際生活并融入思政元素。

1? 定積分概念的引入

我們每天都在使用校園網(wǎng)，可以直接查詢到消耗的上網(wǎng)流量，那如果告訴你某個時間段內(nèi)校園網(wǎng)的網(wǎng)速v（t）=et（mb/s），如圖1所示，你能求出單位時間內(nèi)消耗的流量Φ嗎？

可以看出所求Φ即為圖中曲邊梯形的面積，要求出這個曲邊梯形的面積就需要用到定積分的知識。

其實在1700多年前，我國古代數(shù)學家劉徽提出的“割圓術(shù)”，用圓的內(nèi)接正多邊形面積近似代替圓，求出正多邊形的面積代替圓的面積，他求出3072邊形的面積，得出圓周率約為3.1416，這一方法使此后千年中國圓周率計算在世界上處于領(lǐng)先的水平。“割圓術(shù)”的核心思想就是極限，那么我們能否利用極限這種無限逼近的思想，計算曲邊梯形的面積呢？

首先對圖形做以下劃分，如圖2所示，將曲邊梯形近似看作一個矩形，很顯然，這種劃分方式的誤差太大。

重新對曲邊梯形進行分割，如圖3所示，將曲邊梯形分為5個部分，每個部分用小矩形近似的代替，再求和;很明顯，誤差減小。以這種方式分割的矩形越小，求出的面積誤差越小，那么分割到一定程度使得求出的面積沒有誤差，也就是精確值時，這個問題就解決了。

通過分析，解決此問題的思想就是：將曲邊梯形這個整體分割成局部，用易求出的量近似代替局部量，然后求和得到整體的近似值，最后取極限得到精確值。概括來說就是“分割，近似求和，取極限”，這也是定積分概念產(chǎn)生的背景。

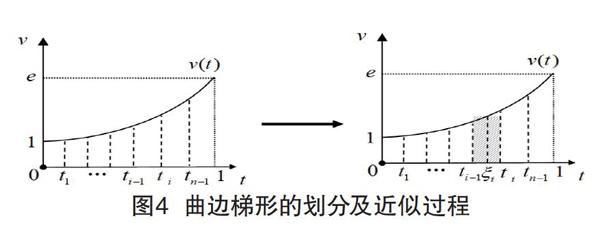
現(xiàn)在用嚴格的數(shù)學語言對問題中曲邊梯形的面積進行求解，如圖4所示。

將區(qū)間[0，1]任意劃分為n部分，令0=t0

當對區(qū)間[0，1]做無限劃分時，上述等式右邊的和式與某一常數(shù)無限接近，則此常數(shù)定義作為曲邊梯形的面積Φ。

如果對一部分區(qū)間[0，ti]做有限劃分，對另一部分區(qū)間[ti，1]做無限劃分，這種情況的誤差依舊比較大;所以為了避免這種情況，對每個小區(qū)間的長度△ti進行約束，記為：

顯然||T||≥△ti，i=1，2，…，n，因此可以用||T||來反映區(qū)間[0，1]被劃分的細密程度。

將區(qū)間[0，1]平均分為n個小區(qū)間時，曲邊梯形的面積也就是單位時間內(nèi)消耗的流量約為：

由以上，現(xiàn)在我們給出定積分抽象概念的完整定義：

設(shè)f（x）是定義在[α，b]上的函數(shù)，J為一個確定實數(shù)，在[α，b]上有n-1個分點，依次為α=x0

再回到例題中，根據(jù)定積分的定義可知，消耗的流量，在后續(xù)學習了牛頓-萊布尼茨公式后，就能很容易地計算出此式的結(jié)果。

2? 定積分概念中蘊含的哲學思想

通過對實際問題的思考，以及借鑒“割圓術(shù)”的極限逼近思想，引出了定積分的概念，并給出定積分的嚴格定義。在這一過程中，我們發(fā)現(xiàn)定積分的思想方法蘊含了辯證法的兩大規(guī)律：通過求和將大的曲邊梯形的面積和經(jīng)過無限劃分過后的小矩形面積統(tǒng)一起來，最初求得面積的近似值與經(jīng)過無限劃分得出的精確值是互相對立的，通過取極限將兩者統(tǒng)一起來，發(fā)生了質(zhì)的飛躍;無論是分割、近似還是求和，得出的都是近似值，這都是量變，但通過取極限得出了精確值，發(fā)生了質(zhì)變。同樣，理解了從局部去解決整體的問題，復(fù)雜的問題都是由簡單的事情組合起來的，我們可以盡可能地將比較難的大問題切分為許多小問題來解決。運用科學的辯證方法能夠幫助我們就解決許多問題，不僅體現(xiàn)在我們的學習中，更是體現(xiàn)在社會主義的建設(shè)中，黨制定的方針、路線的重要理論工具就是量變質(zhì)變規(guī)律，指導(dǎo)我們正確地處理社會主義發(fā)展、改革和穩(wěn)定的關(guān)系，使社會主義獲得更大的發(fā)展。

通過此教學實例可以發(fā)現(xiàn)，將實際應(yīng)用與思政教育融進高等數(shù)學課堂中，改變了基礎(chǔ)課程教學的枯燥印象，在學習專業(yè)知識的同時認知領(lǐng)域更加寬闊，更有利于當代大學生建立正確人生觀、堅定和崇高的理想信念。

參考文獻

[1] 高燕.課程思政建設(shè)的關(guān)鍵問題與解決路徑[J].中國高等教育，2017（Z3）：13-16.

[2] 陸道坤.課程思政推行中若干核心問題及解決思路基于專業(yè)課程思政的探討[J].思想理論教育，2018（3）：64-69.

[3] 閔輝.課程思政與高校哲學社會科學育人功能[J].中國高等教育，2017（15）：21-24.