基于契約理論的移動眾包網(wǎng)絡(luò)長期激勵機制研究

武明虎，萬其軒，趙 楠

(1 湖北工業(yè)大學(xué)，太陽能高效利用與儲能系統(tǒng)運行控制湖北省重點實驗室，湖北 武漢 430068；2 湖北工業(yè)大學(xué)， 湖北省太陽能高效利用協(xié)同創(chuàng)新中心，湖北 武漢 430068)

近年來，隨著IT計算的飛速發(fā)展，移動智能設(shè)備都裝載了大量的傳感器和處理器，能夠?qū)崟r感知設(shè)備周圍環(huán)境的信息[1]。然而，移動用戶(Mobile Users, MUs)在參與完成任務(wù)的同時，接受和傳遞數(shù)據(jù)需要消耗移動用戶智能設(shè)備的資源和時間，例如：內(nèi)存、電量、流量等。并且MUs的一些地理位置、活動軌跡等個人隱私信息會在眾包完成數(shù)據(jù)的傳輸中暴露出來，這就給MUs帶來一定的安全風(fēng)險。所以在沒有滿意的激勵補償?shù)那闆r下，MUs很難積極參與到移動眾包任務(wù)中。因此，移動眾包網(wǎng)絡(luò)(Mobile Crowdsourcing Network, MCN)中為軟件服務(wù)商(Service Provider, SP)設(shè)計合理的激勵方法成為了移動眾包普及的過程中亟需解決的問題。

目前關(guān)于MCN的激勵機制主要有三種，分別是基于服務(wù)、基于貨幣和基于娛樂的機制[2]。基于服務(wù)的激勵機制是眾包參與者可以通過參與眾包任務(wù)獲得聲譽和社會的認(rèn)可[3-5]；基于娛樂的激勵機制意味著將任務(wù)變?yōu)榭赏娴挠螒騕6,7]。基于貨幣的激勵機制就是眾包參與者可以通過參與眾包任務(wù)獲得貨幣獎勵[8-10]。由于前面兩種激勵機制都需要有特定領(lǐng)域的相關(guān)知識，例如人工智能和計算機理論，所以，基于貨幣的激勵機制更適合移動眾包場景。但是，目前的這些研究大多都沒有考慮網(wǎng)絡(luò)信息不對稱的問題，本研究重點關(guān)注信息非對稱下移動眾包網(wǎng)絡(luò)的另一種基于支付的激勵機制——契約理論。

契約理論是研究經(jīng)濟(jì)學(xué)領(lǐng)域中如何在不確定的情況下做出選擇，或者是簽訂的合同中的信息非對稱問題。最近，它已經(jīng)被成功的運用在通信領(lǐng)域以解決現(xiàn)有的許多實際問題，例如協(xié)作中繼問題[11-13]，移動眾包[14]和合作頻譜交易[15]。因此，針對MCN中的網(wǎng)絡(luò)信息非對稱的問題，本文將契約模型引入到MCN的長期激勵機制中，提出了基于契約理論的移動眾包網(wǎng)絡(luò)長期激勵機制，設(shè)計了兩階段移動眾包網(wǎng)絡(luò)的動態(tài)契約模型，結(jié)合激勵相容約束和參與約束的條件，打破簽約雙方的網(wǎng)絡(luò)信息非對稱，以更好地激勵MUs積極參與長期的移動眾包任務(wù)，從而實現(xiàn)SP和MUs互利共贏。

1 系統(tǒng)模型

移動眾包網(wǎng)絡(luò)(圖1)中包含三個基本部分：SP，MUs和任務(wù)發(fā)布者。任務(wù)發(fā)布者首先將他們的任務(wù)需求發(fā)送給SP，SP把這些任務(wù)需求分成若干個小任務(wù)。然后，將這些小任務(wù)發(fā)布在眾包平臺上，來吸引MUs 參與。當(dāng) MUs完成眾包任務(wù)以后，任務(wù)完成數(shù)據(jù)最終將提供給任務(wù)發(fā)布者。

圖 1 移動眾包網(wǎng)絡(luò)系統(tǒng)圖

1.1 MU建模

假設(shè)SP雇傭MU來為其完成移動眾包任務(wù)，則第i個MU付出眾包努力ei為SP帶來的收益xi。考慮到動態(tài)環(huán)境的測量誤差以及環(huán)境中的動態(tài)因子的影響，SP實際獲得的收益xi可以被假設(shè)為噪聲信號，即

xi=μiei+θ

(1)

其中，μi是每單位工作量MU所獲得的收益，θ～N(0,σ2)是服從正態(tài)分布的隨機變量。

采用線性共享策略[16]，于是，SP支付給MU的報酬si可定義為

si=ai+bixi

(2)

其中，ai是第i個MU的基本工資，bi∈[0,1]是基于移動用戶完成移動眾包任務(wù)的獎金系數(shù)。

于是，第i個MU實際獲得的收益wi可表示為其獲得的報酬si減去參與移動眾包任務(wù)所產(chǎn)生的成本Ci(ei)，即

wi=si-Ci(ei)

(3)

考慮到SP獲得的實際收益xi是噪聲信號，MU實際收益wi也近似于噪聲信號且服從正態(tài)分布，其期望為

(4)

方差為

Var[wi]=(bi)2σ2

(5)

在本文中，假設(shè)每個MU都是風(fēng)險規(guī)避型，且具有不變的絕對風(fēng)險規(guī)避效用函數(shù)：f(wi)=-e-ηMwi，其中，ηM表示MU的 Arrow-Pratt 絕對風(fēng)險厭惡程度[17]，并且ηM越大，MU就越害怕風(fēng)險，一般地，0≤ηM≤1。于是，第i個MU的期望效用Ui可表示為

(6)

(7)

1.2 SP建模

SP 的效用us是MU 付出的眾包努力ei而實現(xiàn)的收益減去支付給MU的報酬，可表示為

(8)

進(jìn)一步， SP的期望效用可表示為

方差為

2 信息非對稱場景下兩階段的最優(yōu)契約設(shè)計

圖 2 兩階段動態(tài)契約時序圖

2.1 第二階段的契約設(shè)計

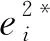
(9)

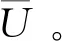
(10)

因此，基于以上的IC和IR約束，SP獲得的最大期望效用的優(yōu)化問題可表示成

(11)

根據(jù)上述IC約束(9)，每個 MU在第二階段應(yīng)該付出的最優(yōu)眾包努力為

最后，對于優(yōu)化問題(11)，通過簡化計算可以得到MU在第二階段獎金提成系數(shù)的最優(yōu)解為

(12)

2.2 第一階段的契約設(shè)計

由于已經(jīng)保證第二階段是最優(yōu)的，因此第一階段的最優(yōu)解問題也就是這兩個階段的總的最優(yōu)解問題。與第二階段最優(yōu)契約設(shè)計相類似，設(shè)計的契約必須要滿足MU兩個階段的IC約束條件

(13)

同樣的，為了保證MU在參與兩階段眾包任務(wù)獲得效用大于或者等于拒絕契約的效用，也就是兩階段的保留效用ui。因此，設(shè)計的契約應(yīng)該滿足IR約束

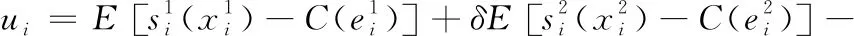
(14)

因此，基于以上的IC和IR約束，SP兩階段可以獲得的最大期望效用可表示為

(15)

根據(jù)IC約束(13)，可以得到MU第一階段應(yīng)該付出的最優(yōu)努力為

因此，對于優(yōu)化問題(15)，通過簡化計算可以得到MU在第一階段獎金提成系數(shù)的最優(yōu)解為

(16)

3 實驗結(jié)果

基于 MATLAB 仿真平臺，通過設(shè)置數(shù)據(jù)參數(shù)，給出數(shù)值結(jié)果來評估基于契約的移動眾包激勵機制的性能。在所有實驗中，參數(shù)設(shè)置如下：ηM= 0.3，σ2= 0.81。 隨著場景的變化，其他變量將設(shè)置不同的參數(shù)值。

(a)第一階段中移動眾包成本系數(shù)變化的最優(yōu)契約設(shè)計

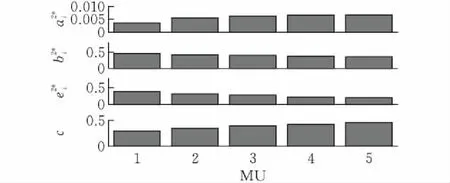
(b)第二階段中移動眾包成本系數(shù)變化的最優(yōu)契約設(shè)計 圖 3 每單位的利潤μi變化時最優(yōu)契約設(shè)計

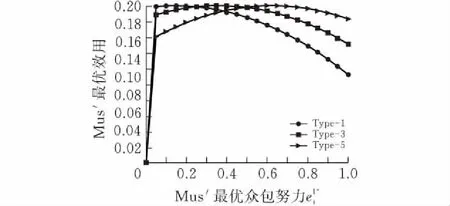
(a)不同類型的MU在第一階段契約設(shè)計下 努力激勵的最佳效用

(b)不同類型的MU在第二階段契約設(shè)計下 努力激勵的最佳效用圖 4 契約設(shè)計下不同類型MU努力激勵的最佳效用

4 結(jié)論

本文針對MCN中的網(wǎng)絡(luò)信息非對稱問題，提出了在動態(tài)環(huán)境下SP與MU之間的移動眾包網(wǎng)絡(luò)長期激勵機制設(shè)計方法。將以市場驅(qū)動為基底的契約模型引入到MCN中，提出了基于契約理論的移動眾包網(wǎng)絡(luò)長期激勵機制來解決移動眾包網(wǎng)絡(luò)中的網(wǎng)絡(luò)信息不對稱的問題。仿真結(jié)果表明，所研究的基于契約的策略可以提高眾包完成質(zhì)量并實現(xiàn)簽約兩方雙贏的結(jié)果。