連續剛構拱橋拱梁墩結合處力學特性研究

劉耀東， 李子昂

(湖北工業大學土木建筑與環境學院， 湖北 武漢 430068)

大跨度連續剛構拱橋是一種新型的組合體系橋梁，主要由拱肋、橫撐、吊桿、主梁構成。拱肋、主梁和墩結合處承受各構件的軸力、剪力和彎矩的共同作用，此部位不僅存在軸力、剪力、彎矩耦合的問題，還存在鋼結構向混凝土結構過渡的問題，受力十分復雜。為確保橋梁結構安全，對這一部位進行精細化有限元受力分析十分必要。

某連續剛構拱橋，左邊為小里程方向，剛構部分孔跨布置為(90+180+90) m，橋寬13.3 m。主梁釆用單箱單室變高度箱形截面。拱橋采用鋼管混凝土拱，計算跨度L=180.0 m，設計矢高f=36.0 m，拱軸線釆用二次拋物線，釆用等高度啞鈴形截面，弦管直徑Φ=1.1 m，弦管之間用鋼綴板連接，拱肋弦管及綴板內填充微膨脹混凝土。連續剛構與鋼管混凝土拱通過剪力釘在拱腳處連為一體。連續剛構拱橋總體布置見圖1。采用先整體后局部的分析方法對拱梁墩結合處進行分析。在對拱梁墩結合處分析之前，首先對全橋進行靜力分析，得到14#號墩上部的拱梁墩結合處各截面內力，然后以結合處為隔離體進行精細化分析。

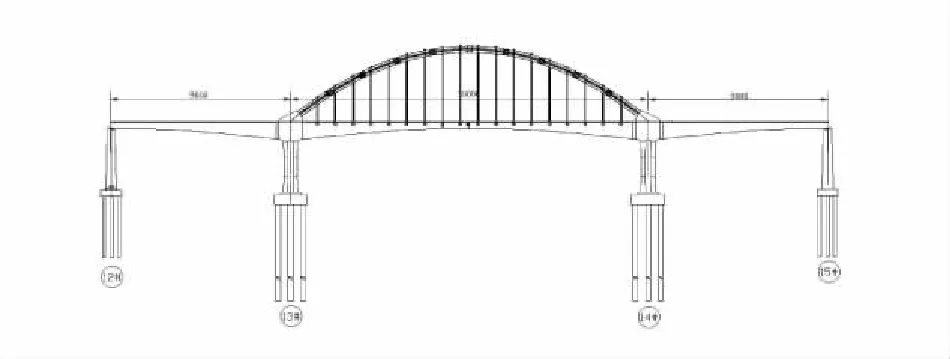
圖 1 連續剛構拱橋總體布置圖 cm

1 全橋靜力分析

采用MIDAS/Civil建立空間桿系模型，計算全橋在恒載和恒載+活載兩種工況下各截面彎矩、軸力見圖2、圖3。

圖 2 橋梁各截面彎矩圖 kN·m

圖 3 橋梁各截面軸力圖 kN

根據圣維南原理(Saint-Venant’s Principle),為消除邊界效應，按以下原則選取有限元模型范圍。主梁截斷處距離拱梁墩結合處的距離大于1.5倍拱梁墩結合處高度和長度，截斷的拱肋伸出結合段的長度大于1.5倍拱肋圓截面直徑[1]。選取14#墩上部主梁距橋墩中心線左右20 m及鋼管混凝土拱伸出拱座2.5 m為模型范圍。圖2和圖3中拱梁墩結合處邊界主梁截面和拱肋截面的內力見表1。 表1中以14#橋墩中心線向右20 m處的橫橋向截面為主梁大里程方向截面，向左20 m處的橫橋向截面為主梁小里程方向截面，以拱肋伸出拱座2.5 m處拱肋橫截面為拱肋截面，以小里程往大里程方向左為左側拱肋，右為右側拱肋。在進行結合處模型局部分析時，表1中所列的不同內力作為外荷載加載在拱梁墩結合處相應的截面。

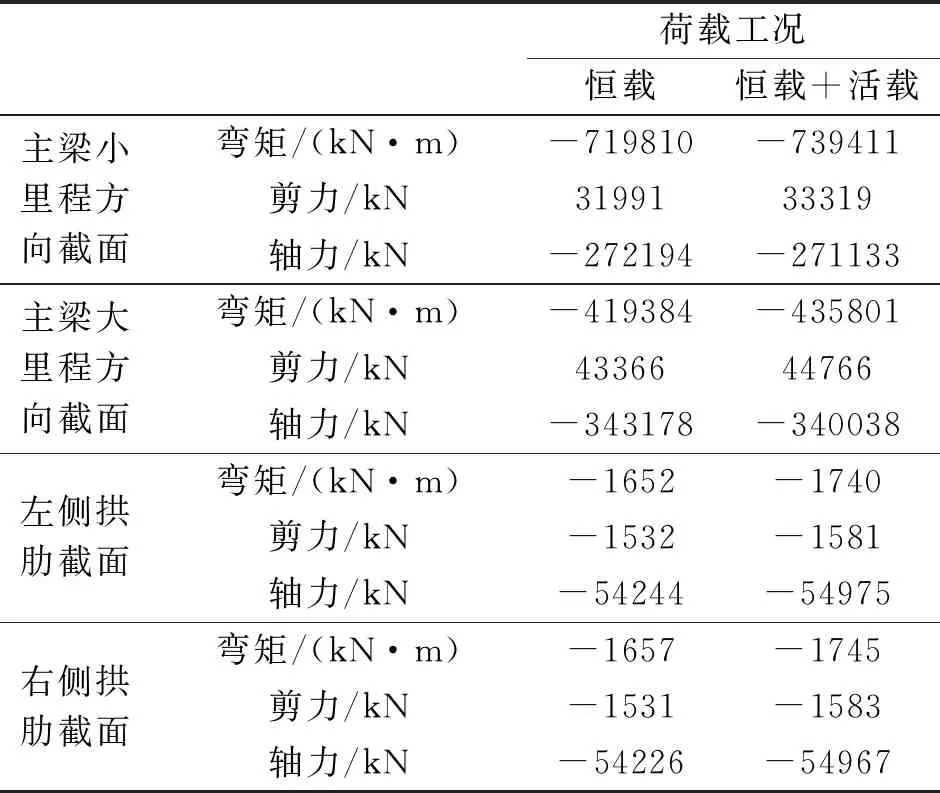
表1 拱梁墩結合處邊界內力

2 拱梁墩結合處有限元計算

2.1 結合處有限元模型

采用MIDAS/FEA進行拱梁墩結合處細部分析，基本假定如下：

1)構件的應力應變符合胡克定律。

2)結合處所采用的鋼筋和混凝土均為各向同性材料。

3)對于普通鋼筋不予考慮。

4) 對于鋼材與混凝土之間的滑移不進行考慮。

5) 對于由于制造加工引起的偏心、缺陷和殘余應力等不予考慮[1]。

建模材料參數[2]見表2。

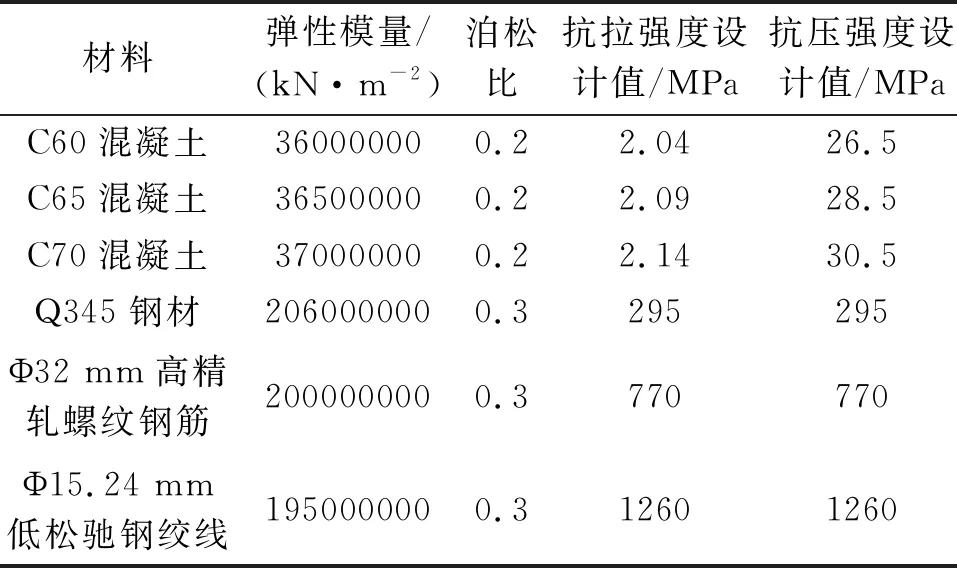
表2 有限元模型材料參數

該模型混凝土和鋼拱肋采用實體單元模擬，預應力筋采用桿單元模擬。拱座處是受力復雜區域，對該處網格劃分予以加密。對于鋼管混凝土拱肋和混凝土接觸部分，剪力釘為鋼管混凝土拱肋與混凝土間的彈性連接件。計算模型中未采用剪力釘單元,利用拱肋鋼塊體單元與混凝土塊體單元共節點的方式進行模型單元劃分[3]。共劃分節點143 054個，單元256 548個。將雙薄壁墩底面假定為固結，將主梁小里程方向截面、主梁大里程方向截面、鋼管混凝土拱肋截斷處截面設為邊界。將邊界截面單元節點與截面形心節點通過剛性連接連為一體形成剛性面，施加邊界內力于形心節點，以此來模擬截面荷載的作用方式。拱梁墩結合處有限元模型見圖4。計算工況為成橋階段恒載作用下的工況和恒載+活載作用下的工況。

圖 4 拱梁墩結合處有限元模型

2.2 計算結果分析

兩個工況的計算結果都表明拱梁墩結合處受力復雜，大部分處于受壓狀態，且壓應力在合理范圍內。選取恒載+活載工況作為最不利工況，從變形和受力兩方面對拱梁墩結合處進行分析[4-5]。

2.2.1 拱梁墩結合處位移變形分析兩工況下的計算結果表明位移符合規范要求。由圖5可知最大位移9 mm出現在小里程端處，其原因是拱肋對拱座處斜向壓力及小里程端處的軸向壓力共同作用。該位移變形對結構影響較小，符合規范要求。

2.2.2 拱梁墩結合處應力分析恒載+活載工況下計算結果表明拱梁墩結合處大部分均處于受壓狀態。由圖6、圖7可知主梁壓應力分布沿順橋向中心線對稱，主梁的腹板為主要受壓構件。混凝土部分承受最大壓應力值27.89 MPa出現在右半邊薄壁墩與主梁固結處，超出混凝土抗壓強度設計值26.5 MPa。由于此壓力僅出現在局部很小的區域，且計算中未考慮應力重分布現象，因此該部位應力超限不會對結構產生安全影響。最大拉應力1.23 MPa出現在左半邊薄壁墩處，此拉力滿足規范設計要求。

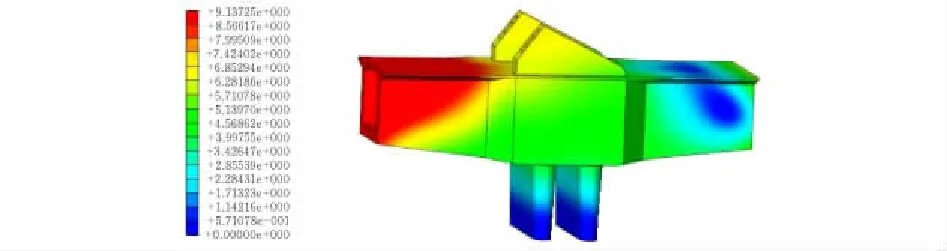
圖 5 恒載+活載工況下位移云圖 mm

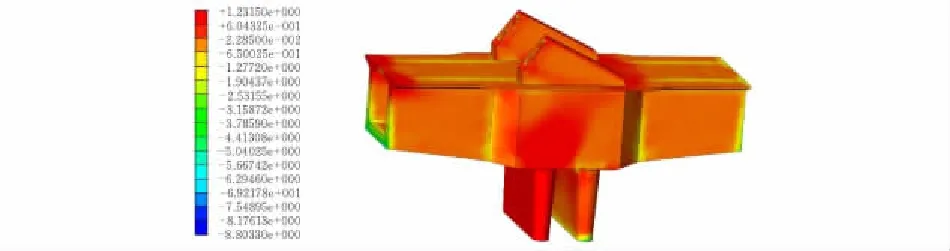
圖 6 恒載+活載工況下主拉應力云圖 MPa

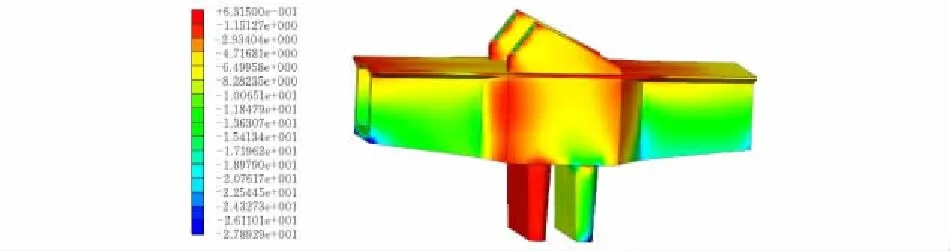
圖 7 恒載+活載工況下主壓應力云圖MPa

在整個結合處中，拱座部位應力分布最復雜。除拱座處轉角和底部應力分布均勻，其余部位應力分布復雜。由圖8可知，鋼管混凝土拱和拱座混凝土接觸部分產生明顯的應力集中，綴板內混凝土與拱座混凝土接觸部位應力相對過渡平緩。這表明兩種剛度相差較大的材料接觸承壓時會產生接觸面變形不協調，從而引起局部應力過大，而兩種剛度近似或相同的材料接觸承壓時會緩解應力集中現象。同時，綴板內灌注混凝土導致混凝土相互接觸面積較大，也在一定程度上緩解拱座處的應力集中現象。由于在拱座處隨著遠離鋼管拱和混凝土接觸部位應力迅速變小，因此在拱座設計時應主要考慮鋼管混凝土拱和拱座接觸部位。

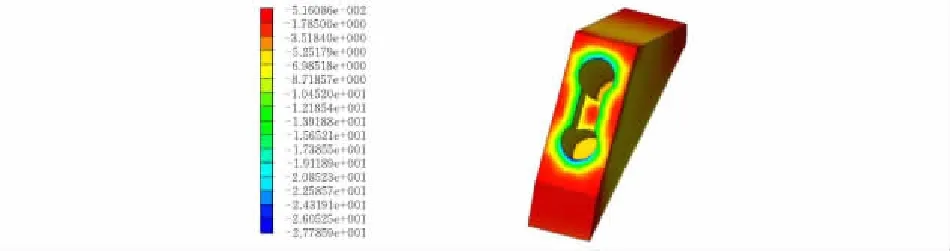
圖 8 恒載+活載作用下拱座應力云圖 MPa

對于鋼管拱肋分析，由圖9可知，拱肋處應力隨著深入拱座混凝土而減小。這是由于拱肋與拱座混凝土通過剪力釘連接，使得澆筑在拱座中較淺的拱肋承擔更大的應力。因此剪力釘在設計時可以采用上密下疏的方式來優化。拱肋中的應力最大值126.89 MPa出現在拱肋截斷面處。由于外力作用在此處未完成應力擴散所以造成此處應力集中。這一值滿足規范要求。

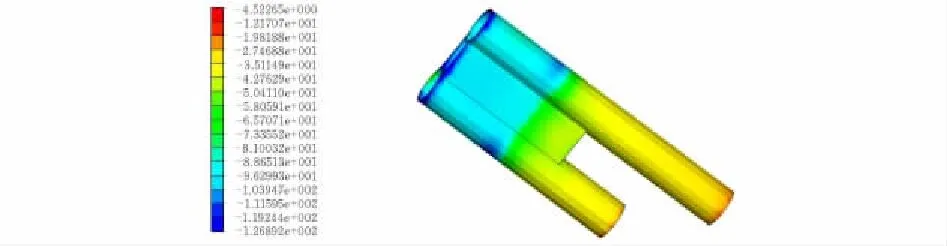
圖 9 恒載+活載作用下拱肋應力云圖 MPa

表3 拱梁墩結合處大應力出現位置

部位結構所處位置部位1雙薄壁左墩部位2雙薄壁墩與主梁固結右端部位3拱肋與拱座接觸面部位4拱肋截斷面處部位5綴板內砼與拱座砼接觸處

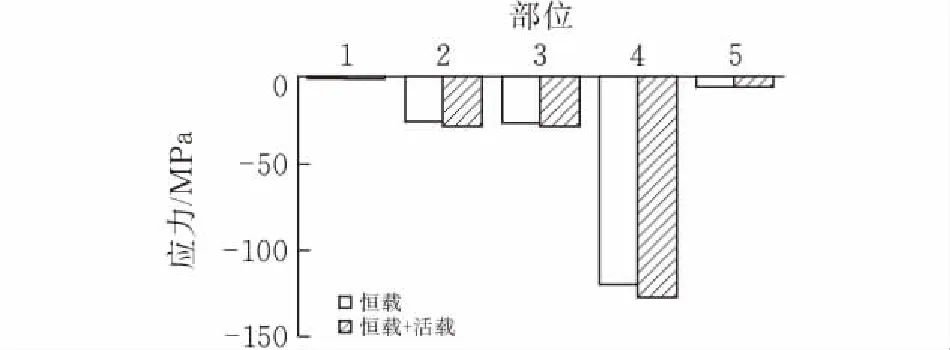
圖10 不同工況關鍵位置大應力柱狀圖

經過計算對比，在恒載工況下，拱梁墩結合處應力分布區域和恒載+活載工況下的應力分布區域相似。恒載+活載工況下結合處出現大應力的部位見表3，通過柱狀圖比較兩種工況下大應力的區別。由圖10可知，在恒載+活載工況下不同位置的大應力和恒載工況下大應力基本一致。差值范圍在1.5%～7.4%之間。

3 拱梁墩結合處改良

圖8中，鋼管混凝土拱和拱座混凝土接觸部分產生明顯的應力超過混凝土抗壓強度設計值，針對這一現象，為改善拱座處受力，采用提高混凝土強度等級為C65和C70和加焊拱肋端頭應力擴散板這兩種方式進行試驗，研究這兩種方式是否對拱座受力有改善作用。

3.1 對鋼拱肋底端加焊應力擴散板

對已加焊應力擴散板的鋼拱肋進行重新建模見圖11。

圖11 拱肋改善有限元模型

僅計算模型在恒載+活載工況下的拱座應力分布見圖12。

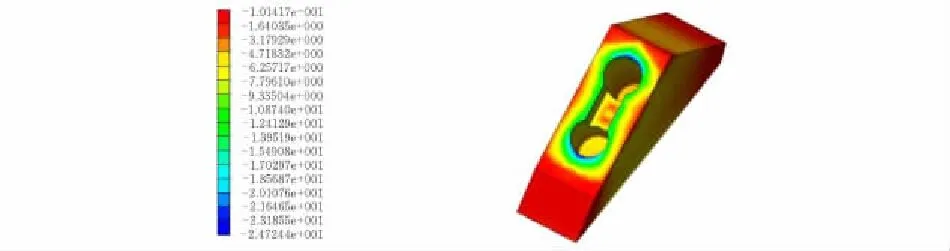
圖12 改善拱肋拱座應力圖 MPa

比較圖12和圖8可知，加裝應力擴散板拱座的應力云圖與未加裝應力擴散板拱座的應力云圖相似。對比數值發現，拱肋與拱座接觸部位的最大壓應力由27.79 MPa降至24.72 MPa，小于混凝土抗壓強度設計值26.5 MPa，應力降幅達10.5%。

3.2 提高混凝土等級

依次計算模型在恒載+活載工況下采用C60、C65、C70三種混凝土等級情況下的模型應力分布，將關鍵位置的應力情況列出見表4。

由表4可知，提高混凝土等級對模型應力的分布影響不大，應力差值范圍在0～3.9%。模型采用C65或C70混凝土計算所得混凝土最大壓應力均小于相應混凝土抗壓強度設計值。但與加裝應力擴散板相比，后者更為經濟方便。

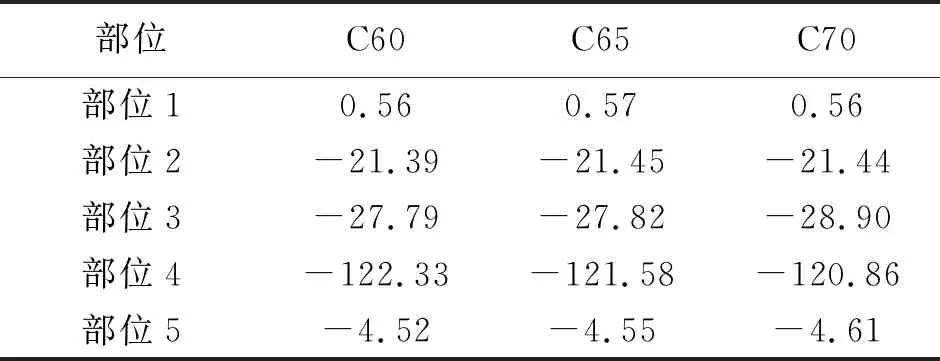
表4 不同混凝土等級下模型應力 MPa

4 結論

通過對連續剛構拱橋拱梁墩結合處的分析計算，得到以下結論與建議：

1)該連續剛構拱橋的拱梁墩結合處大部分處于受壓狀態，安全性基本滿足規范要求。

2)鋼管拱肋拱腳處應力大小隨著深入拱座混凝土而減小，建議剪力釘可以采用上密下疏的方式布置。

3)在拱肋底端加焊應力擴散板對拱座處受力改善較為明顯。