一種針對時滯系統的改進智能軌跡導引控制算法

王文標，王 靖，汪思源，李延超

(大連海事大學船舶電氣工程學院，大連 116026)

在許多工業現場，被控系統的大時滯現象非常普遍且嚴重，時滯的存在惡化控制系統性能，嚴重時甚至會導致系統失穩。

經典PID(proportion-integral-differential)控制在針對大時滯系統時不再適用，因此該領域的研究一直是中外控制專家關注的熱點，傳統的控制方法如Smith預估控制[1]等，從理論上解決了大滯后系統的控制問題。但由于算法嚴重依賴模型的精準度，使其在實際工業中難以應用[2]。隨著模糊控制，神經網絡等與Smith結合，上述現象有所改善[3-5]，但算法復雜度升高，在實際中不能推廣運用。

21世紀初，韓京清提出了自抗擾控制(active disturbance rejection control, ADRC)技術[6]，針對時滯系統提出了無視時滯法，一階慣性環節近似法，輸入預測法和輸出預測法四種方法。此后ADRC技術被廣泛應用于滯后系統的控制[6-7]，中外學者結合ADRC，研究了Smith預估和線性ADRC相結合設計問題[8]。

但鑒于傳統的ADRC在實際工業應用中還可簡化，提出一種新型控制器[9]——智能軌跡導引控制(intelligent track guiding control, ITGC)算法，在經典PID的基礎上引入“合理的過渡過程”，將提取到的微分信號的偏差量按照“適當的組合方式”來改善控制性能和閉環系統的品質，對比ADRC更具有結構簡單、編程容易實現等優點。

然而，在控制大時滯系統時，ITGC依然存在著一定缺陷。雖然選取合適的導引(如加大過渡過程)可以使偏差更加柔和，柔和的偏差使控制量柔和，緩解了時滯給系統帶來的難控問題。但由于只是針對時滯做了近似和妥協，而未從根源上針對時滯對系統的影響，致使導引時間常數取小則系統跟隨性和抗擾性差，取大造成系統調節時間變長。

為此，設計改進智能軌跡導引控制(改進ITGC)算法，通過參考模型和估計滯后的引入，控制器則選取新的偏差來糾正系統響應。利用圖解和公式分析算法在控制大時滯被控對象時具有調節時間短以及抗擾性強的機理，通過仿真以及實物驗證改進ITGC算法在控制大時滯系統時所具有的優越性，并驗證被控對象模型失配時，算法的有效性。

1 ITGC算法描述及偏差選取的優劣

1.1 時滯被控對象

標準的單位反饋時滯系統如圖1所示，被控對象拆分為無滯后被控對象環節和滯后環節。

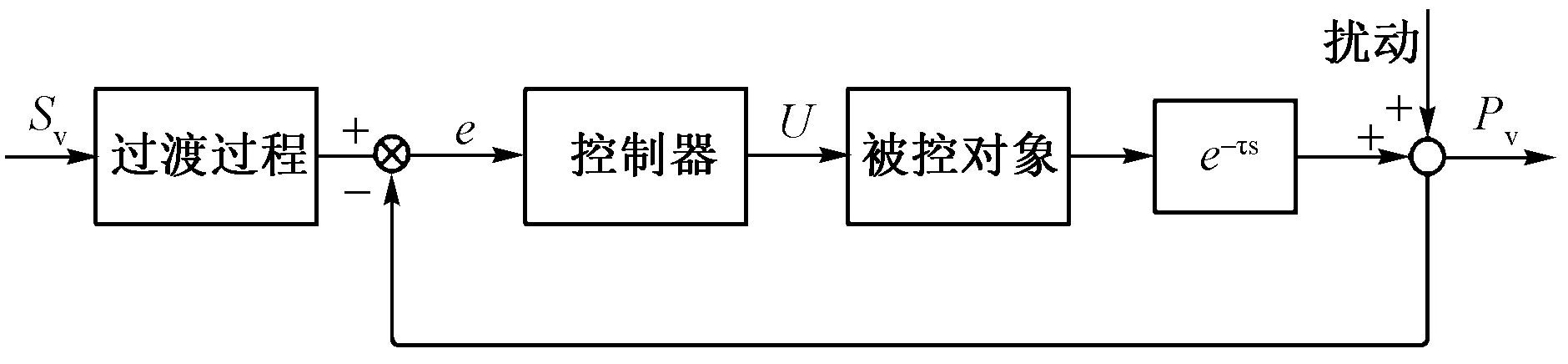
Sv表示設定值；e表示誤差；U表示控制量；e-τs為滯后環節；Pv表示實際值

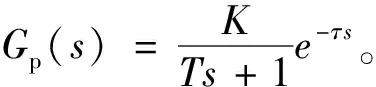
1.2 ITGC算法原理

ITGC算法在繼承PID精髓的基礎上，圍繞“基于偏差來消除偏差”的核心思想，細化為分解總偏差而不斷消除子偏差，以此結合自抗擾技術的思想“為系統規劃合適的過渡過程來導引被控變量”。在閉環控制系統的控制回路中,偏差信號的適當處理決定控制器消除此偏差的控制力[10]。

ITGC算法原理如圖2所示，以過渡過程取一階慣性環節為例，ITGC算法克服了經典PID算法中偏差取法過于簡單的不足，避免了系統輸出值與給定階躍信號之間過大的偏差。

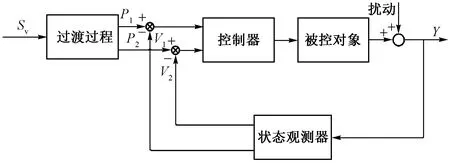
圖2 ITGC算法原理

ΔUn=Ap(P1-P2)+Av(V1-V2)

(1)

V1=(P1-P′1)/ts

(2)

V2=(P2-P′2)/ts

(3)

式中：n為采樣序號(n=0，1,2，…)；ΔUn為ITGC控制器輸出的增量；Ap為位置權重系數；Av為速度權重系數；P1為導引輸出值；P2為系統輸出值；V1為當前導引速度值；V2為當前系統速度值；P′1、P′2分別為P1、P2的前一時刻值；ts=1 s為系統采樣周期。ITGC將控制過程從原來的“目標控制”轉換到“過程控制”，偏差取法比傳統PID偏差選取合理，對時滯系統的控制更柔和適用。

1.3 ITGC算法偏差選取的缺陷

時滯系統偏差選取對比如圖3所示，垂直虛線與時間軸交點為t(s)時刻。

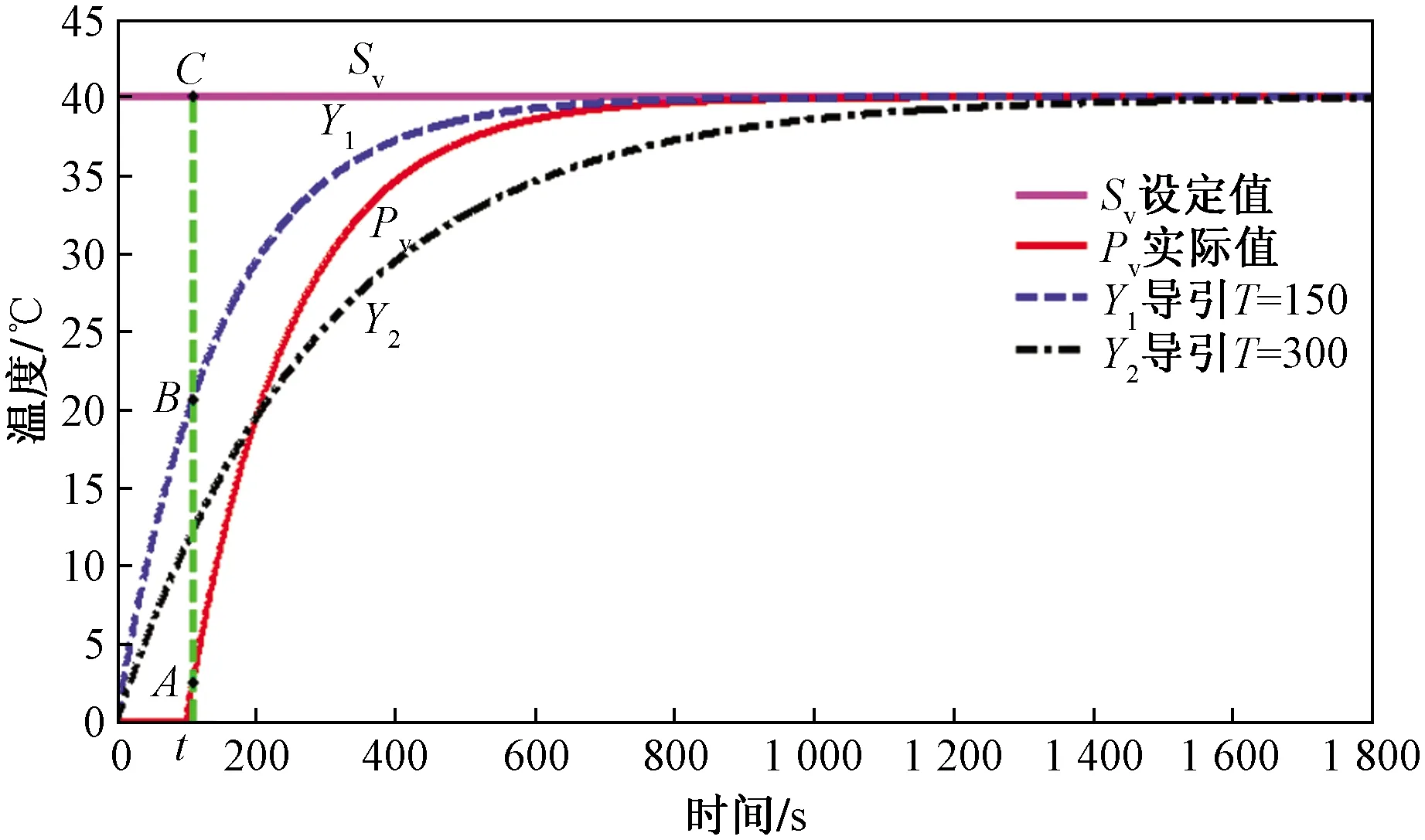
圖3 時滯系統偏差選取

PID控制器選取的偏差為t時刻點C與點A的位置差，對于ITGC來說，偏差為t時刻點B與點A的位置差和速度差。當規劃合理的過渡過程時，ITGC算法相對PID能夠考慮時滯的影響，控制更柔和。

雖然ITGC算法在偏差取法上具有比經典PID算法更合理的優勢，然而面對大時滯系統則存在針對性不強的缺陷。若ITGC過渡過程時間常數Tf取值過小，點B與點A的偏差選取不再合理。圖3中被控對象響應曲線為Pv，被控對象T不變，當τ從100 s增至400 s時，如仍取Y1為導引，則偏差選取與PID偏差選取接近，過程控制轉變為目標控制，偏差選取不合理。需增大導引Tf，取曲線Y2，將目標控制轉化為ITGC所倡導的過程控制。針對大滯后系統更容易使其穩定，但Tf增大規劃的導引曲線達到設定值的時間將增大，從而導致系統調節時間增大。顯然ITGC偏差選取存在了不合理性。

由此說明ITGC算法針對大時滯系統時偏差選取相比經典PID有所改善，但也存在明顯的不合理性。

(4)

(5)

P(s)=Y(s)-Pv(s)

(6)

(7)

式中：Sv為系統的設定值；Pv(s)為輸出；U(s)為控制器輸出；Y(s)為導引輸出；P(s)為當前位置差；P′(s)為前一時刻的位置差；V(s)為當前速度差，令導引時間常數Tf=T。

由式(4)～式(7)，偏差選取從PID每時刻的Sv-Pv(s)變為ITGC的Y(s)-Pv(s)，偏差選取更柔和。取采樣周期ts=1 s，滯后τs即延遲τ拍。Y(s)與Pv(s)相差τ拍，被控量與導引模型的位置存在著不同步，即位置的不同步和速度的不同步，造成偏差選取的不合理。因此在控制大時滯對象時，ITGC算法比經典PID具有優勢，但需做算法改進。

2 改進ITGC算法及其偏差選取優勢

2.1 改進ITGC算法原理

改進ITGC算法原理如圖4所示，安排無滯后過渡過程進行導引，引入無滯后參考模型和滯后估計給定值，DA為規劃導引與無時滯參考模型間的偏差，權重為KA；DB為有時滯給定與實際被控對象間的偏差，權重為KB。控制器選取DA和DB的加權線性組合來糾正系統的響應，控制器輸出的增量式為Δu=KADA+KBDB(KA>10KB)。

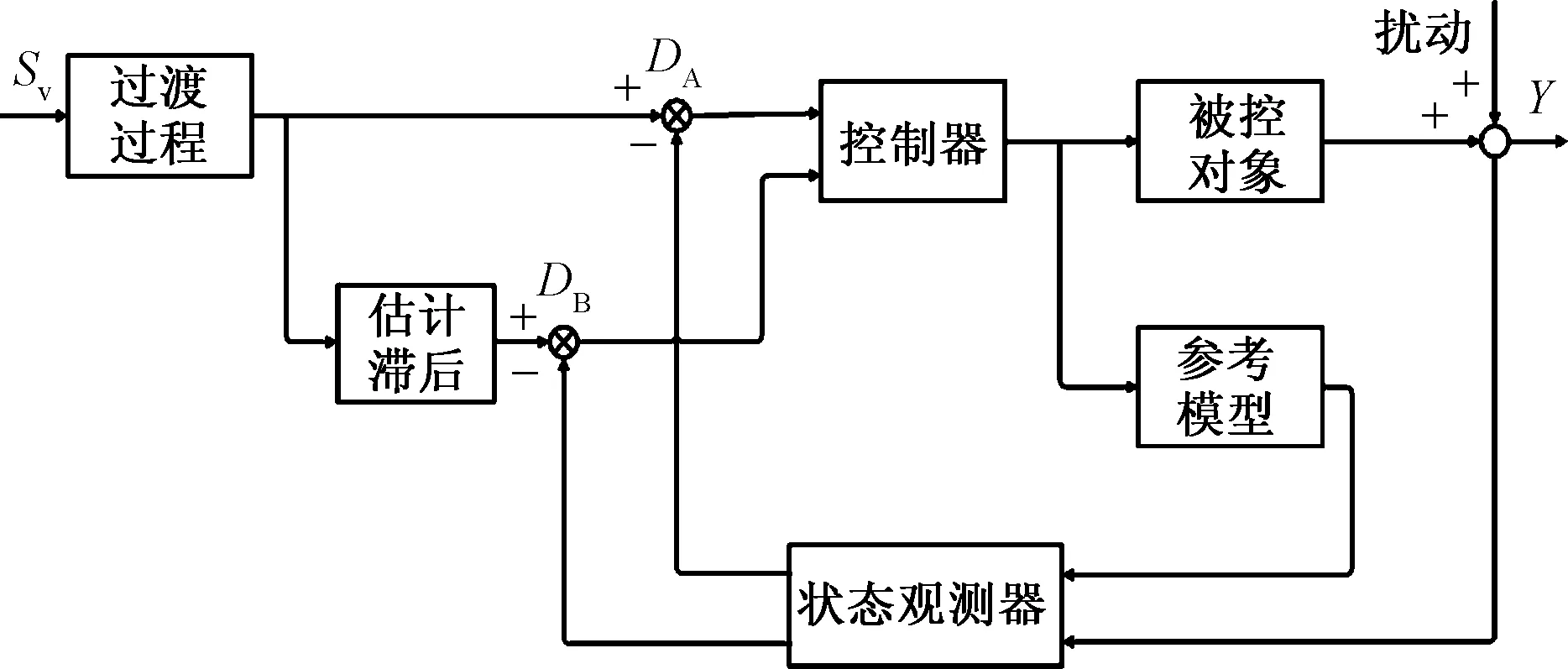
圖4 改進ITGC算法原理

2.2 改進ITGC算法的優勢

2.2.1 ITGC算法的控制效果

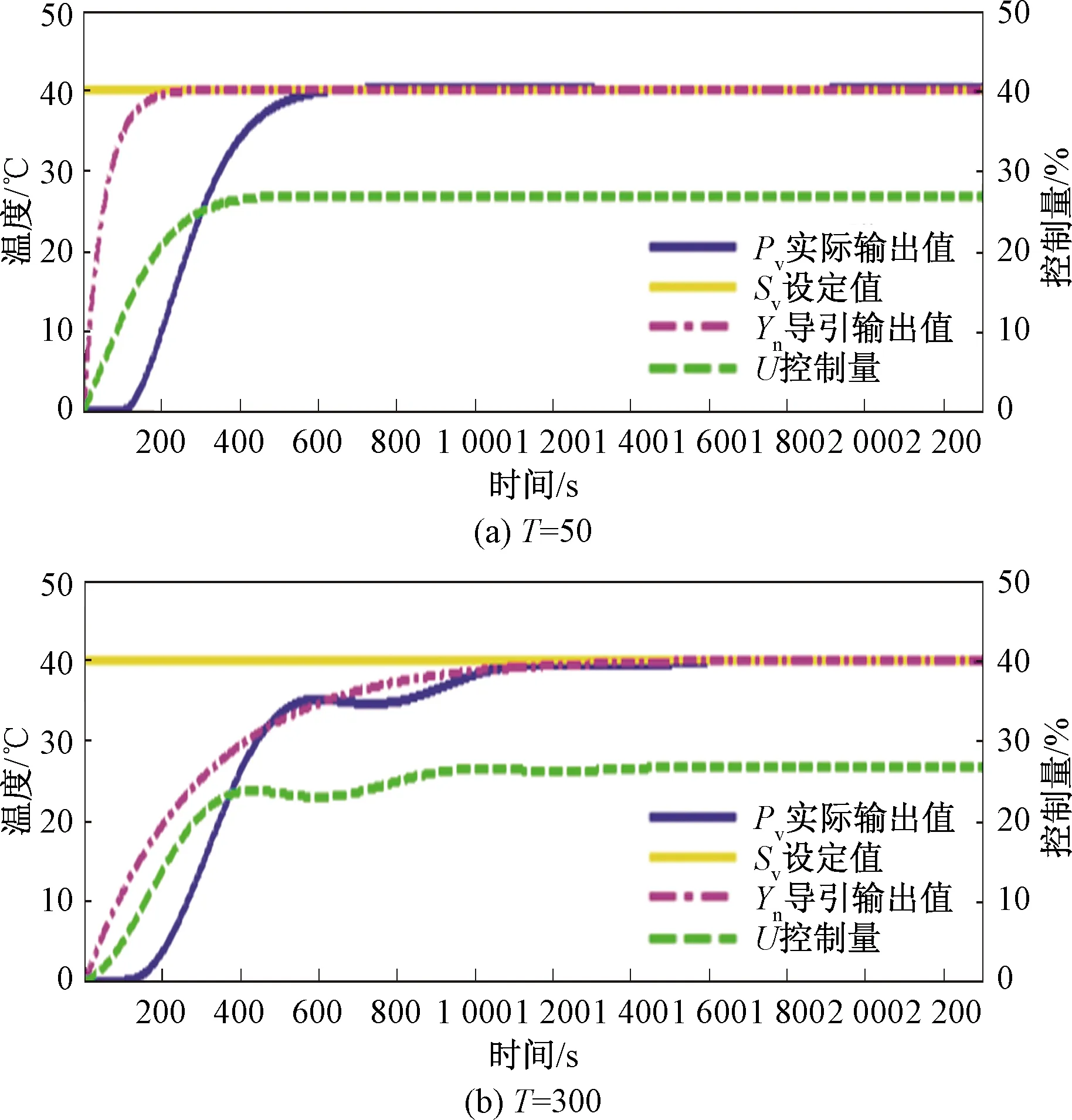
圖5 不同導引下ITGC控制效果

由于時滯存在，T=50取值過小，系統輸出跟不上導引，增大T，當T=300得到其合適值。

2.2.2 改進ITGC算法的控制效果

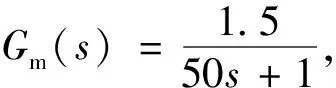
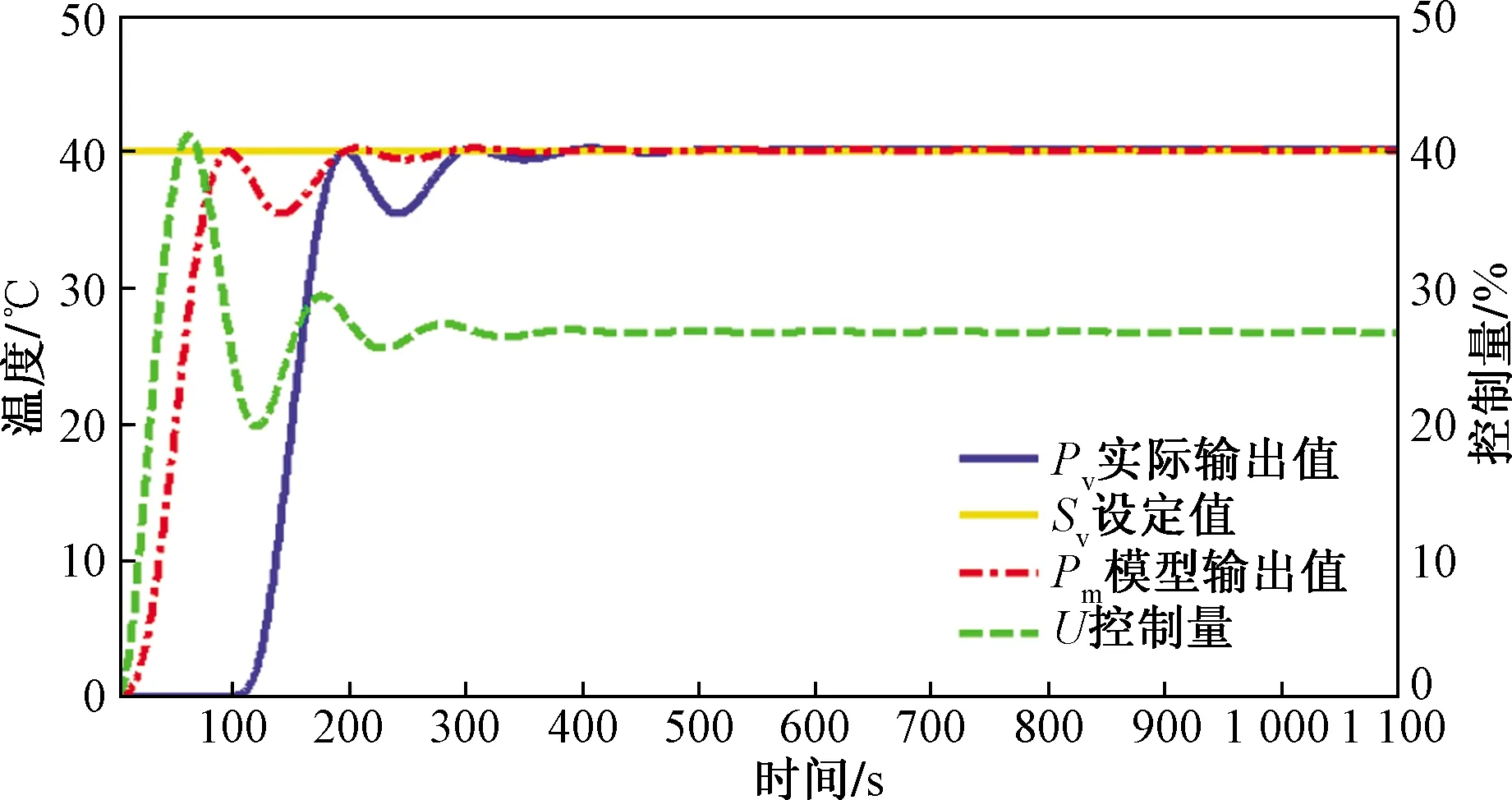
圖6 改進ITGC控制效果

2.2.3 ITGC和改進ITGC下系統性能對比

根據ITGC和改進ITGC控制效果，得出表1所示兩算法控制性能指標對比。

表1 控制性能指標對比

對于ITGC算法，導引時間常數過小系統輸出跟不上導引，調節時間短但平穩性差；反之時間常數大系統能跟隨導引，但調節時間長。而改進ITGC算法既保證了系統響應速度又兼顧其平穩性。

該梁橋長期承受較大的車輛荷載，同時由于混凝土收縮徐變和預應力筋的施工放張工藝等的影響，橋梁鉸縫處破壞嚴重，梁體跨中附近出現橫向裂縫，間距約30～50cm，最大裂縫寬度0.08mm。該橋評定為危橋，進行拆除處理。為研究既有板梁的力學性能及預應力鋼絲繩的加固效果，在對原橋進行拆除時，從中選取1片中部位置的空心板進行荷載試驗。該預應力混凝土空心板跨徑為19.94m，梁體為工廠預制生產，混凝土及鋼筋材料特性見表1。試驗板計算跨徑為19.28m，橫截面寬1.24m、高0.9m。內部預應力鋼絞線7束φ15.2mm，采用后張法施工，錨具為OVM15-7。試驗梁的詳細尺寸見圖1。

2.2.4 改進ITGC算法優勢的描述

針對以上ITGC和改進ITGC控制效果，分別給出如圖7和圖8所示兩算法偏差選取圖。

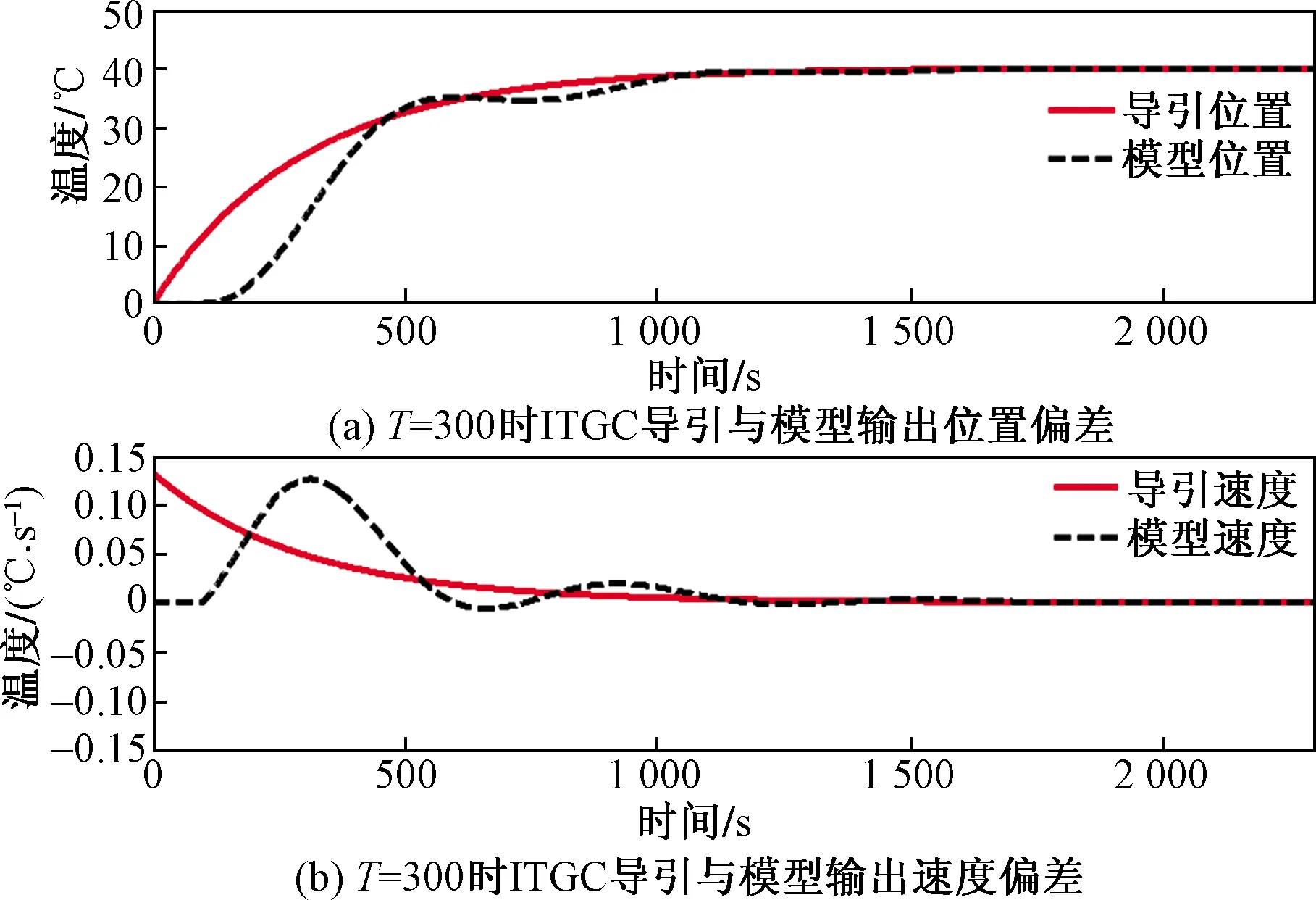
圖7 T=300 ITGC偏差選取

圖8 改進ITGC偏差選取

ITGC控制器偏差選取圖7(a)、圖7(b)兩圖中曲線所圍面積的線性和；改進ITGC控制器偏差選取圖8(a)、圖8(b)兩圖中曲線所圍面積的線性和。此面積一般被定義為控制器的控制面積，面積小則控制柔和，不考慮兩算法偏差權重及正負號，ITGC和改進ITGC控制面積分別為4 687.6和2 866.8，改進算法只有原算法的61%。

ITGC對于被控對象時滯的處理是通過增大導引時間常數使控制量柔和，但未能針對性的消除時滯給系統帶來的影響。而對于改進ITGC，DA先于DB，控制器先根據DA對模型進行控制，模型先于實際被控對象進入穩態，同時為實際被控對象快速找出所需控制量的近似值；DB產生以后，控制器根據DB進行微調，使控制量達到實際被控對象所需設定值的精確值。既保證了控制的柔和，也保證了對大時滯被控對象的響應速度。從根本上消除了時滯帶來的控制難度，提高了控制精度和控制品質。

當系統受到擾動時，DA先保持不變，DB經過τs后變為一個較大的值，此時控制量改變，從而導致DA變為較小且與DB符號相反的值，因KA>10KB，使控制量不會出現較大的改變，當擾動消失時系統可以快速回歸原平衡狀態，系統抗擾性有了很大提升。

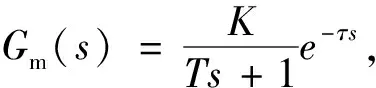
(8)

Y(s)-PM(s)=PA(s)

(9)

Y(s)e-τs-Pv(s)=PB(s)

(10)

U(s)Gm(s)=PM(s)

(11)

(12)

(13)

式中：PM(s)為模型輸出；PA(s)為復數域下DA的值；PB(s)為復數域下DB的值；KA和KB分別為其分配權值。

由式(8)～式(10)，得式(12)和式(13)，對于連續拍系統兩個偏差都是相對較小的值，且DB滯后于DA；實際被控對象輸出同樣滯后于給定模型輸出，因此模型先進入穩態并得出控制量的近似值。對模型的控制指導了對實際對象的控制，實際對象跟隨模型后穩定，保證了控制的快速性及準確性。當擾動進入時，由式(10)，Pv(s)經τs后改變，PB(s)發生變化使U(s)改變，從而使PM(s)改變，導致PA(s)和PB(s)符號相反，當對模型有較準的預估時，即以參考模型為主進行考慮，選取合適權重能夠對U(s)偏離有一定程度抑制，系統抗擾性增強。

3 仿真實驗及實物驗證

3.1 時滯增大算法控制效果仿真對比

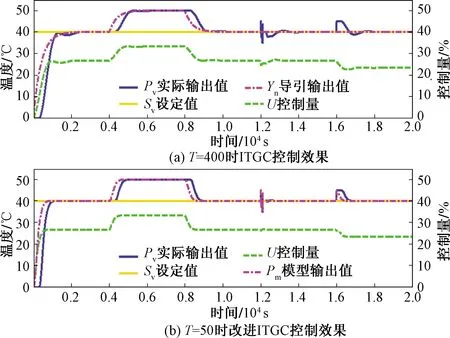
圖9 算法控制對比

針對不同時滯對象，兩算法最佳控制效果下的系統性能指標如表2所示。

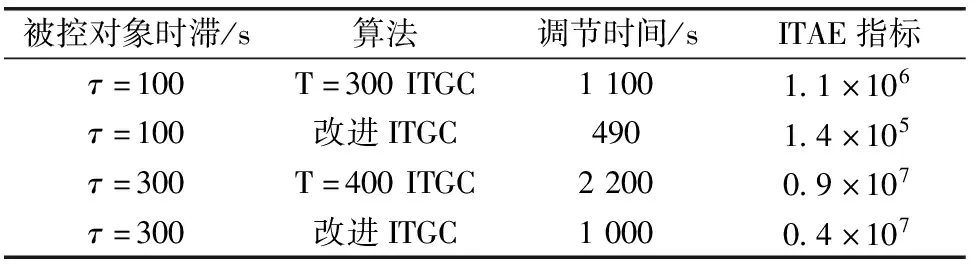
表2 算法性能指標

由圖9和表2，隨著被控對象時滯的增大，系統的控制難度增大，而改進ITGC所需調節時間為原算法的45%。針對同一被控對象，改進算法各項性能指標均占優。并且在設定值跟蹤和抗擾性能方面，改進算法也占優。

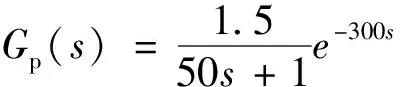
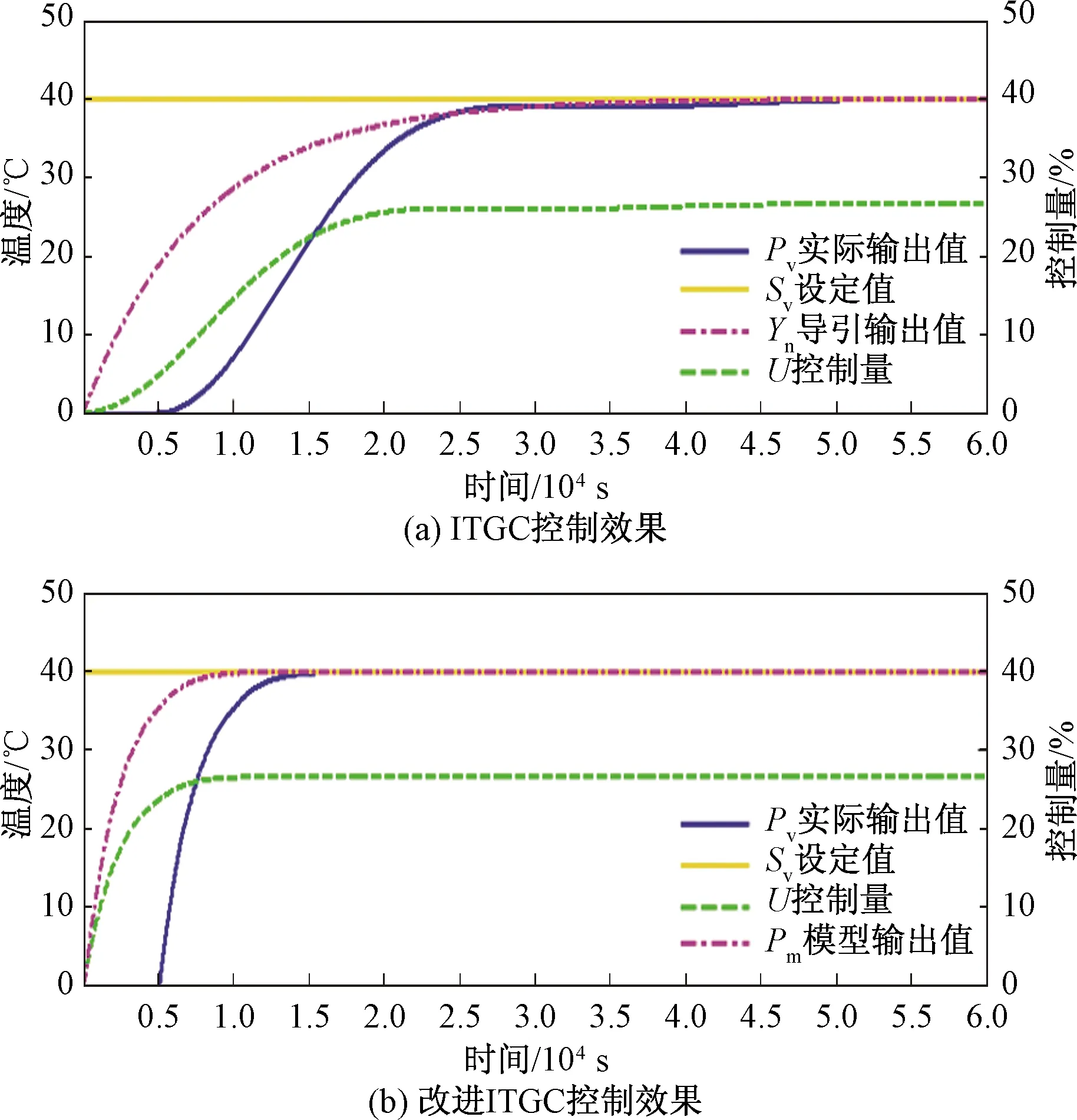
圖10 τ=5 000算法控制對比

在超大時滯下，改進算法調節時間不到原ITGC的1/3。且由圖5、圖6和圖9推知改進算法依然有更好的抗擾性能，限于坐標長度不再驗證。

3.2 模型失配時改進ITGC的仿真控制效果

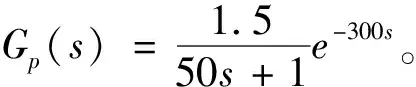
(1)當參數K發生失配時控制效果如圖11所示。

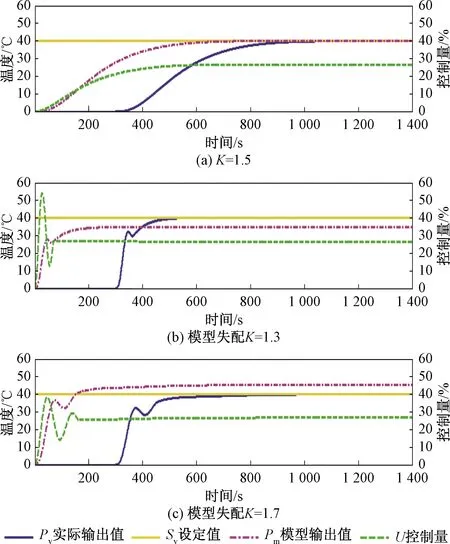
圖11 K失配下改進ITGC控制效果

K存在失配時，改進ITGC算法仍有很好的控制穩定性，但會出現靜差。實際應用過程中，需在被控模型進入穩態時將參數KA切換至0，通過KBDB微修正保證實際被控對象輸出無靜差。

(2)當參數T發生失配時控制效果如圖12所示。

T存在失配，通過整定控制器參數，改進ITGC算法仍有很好的可控性。

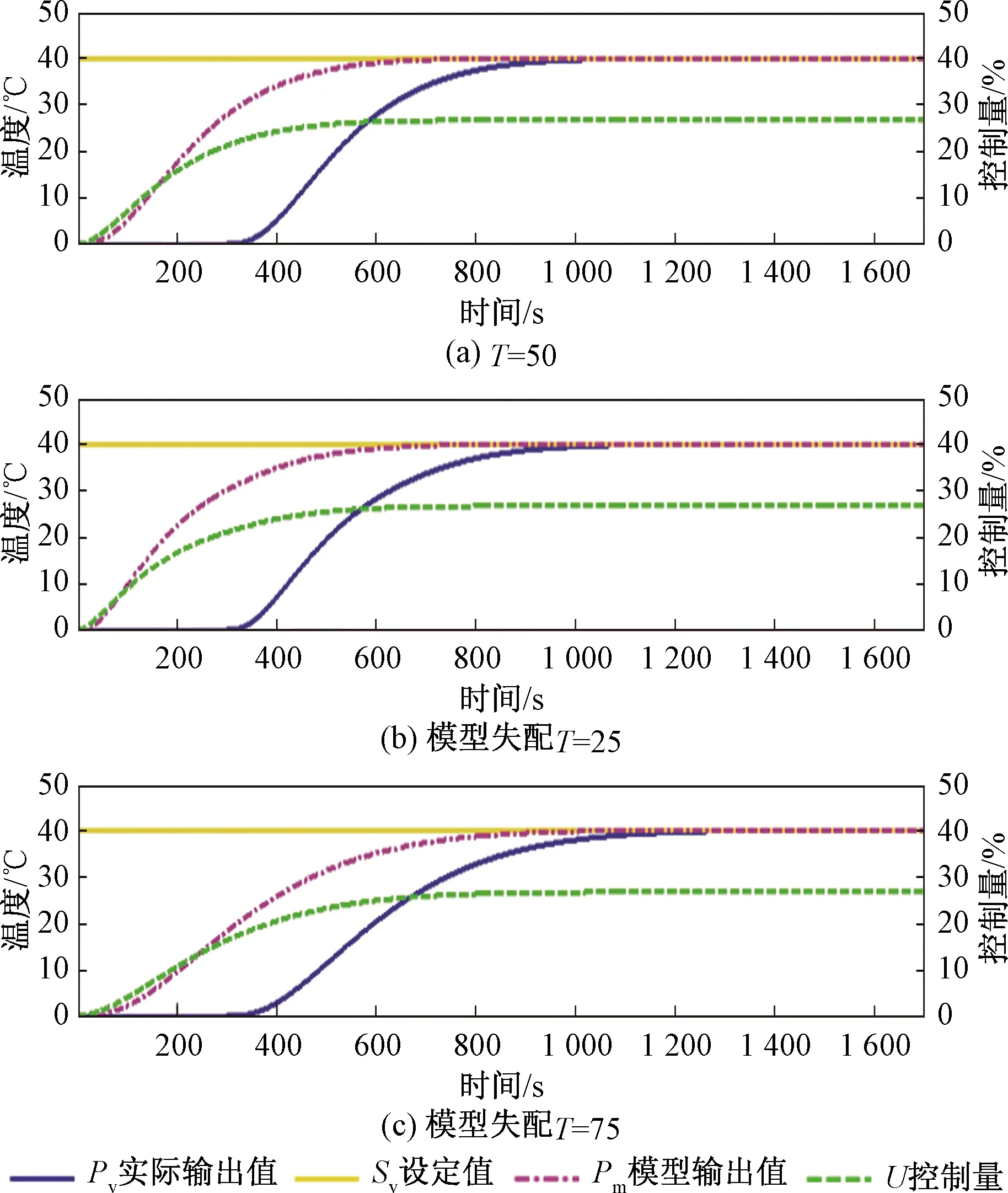
圖12 T失配下改進ITGC控制效果

(3)當參數τ發生失配時控制效果如圖13所示。

圖13 τ失配下改進ITGC控制效果

τ存在誤差，通過整定控制器參數，改進ITGC算法仍有很好的可控性。

3.3 實物驗證

采用如圖14所示一體化試驗箱實驗裝置。被控量為箱體內溫度，通過控制燈泡的功率給定不同的輸出熱量，實現對被控量溫度的調節。實驗裝置被控對象可看作一階慣性環節，在MCGS(monitor and control generated system)中寫入數字滯后將被控對象變為FOPDT形式。

圖14 一體化試驗箱

3.3.1 一體化試驗箱飛升實驗建模

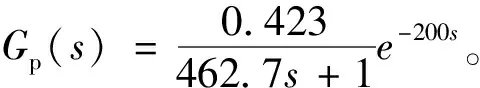
3.3.2 一體化試驗箱下的ITGC算法控制實驗

初始設定溫度在45.0 ℃，系統穩定后在6 200 s時加入+5.0 ℃的設定值跟蹤實驗，在10 080 s加入10 s風扇擾動觀察算法抗擾性能。ITGC算法實物控制效果如圖15所示。

圖15 ITGC算法實物控制效果

3.3.3 一體化試驗箱下的改進ITGC算法控制實驗

初始設定溫度在45.0 ℃，系統穩定后在4 500 s時加入+5.0 ℃的設定值跟蹤實驗，待系統再次穩定后在6 520 s加入10 s風扇擾動觀察算法抗擾性能。改進ITGC算法實物控制效果如圖16所示。

圖16 改進ITGC算法實物控制效果

3.3.4 一體化試驗箱下兩算法控制效果對比

由于對一體化試驗箱進行溫度控制容易受到現場環境的影響，所以實驗默認系統被控量誤差在0.5 ℃以下為達到穩態。表3給出了兩算法在控制實物時的控制效果對比。

由表3可知，改進ITGC在針對實際的大時滯被控對象進行控制時，對比原ITGC各項指標均占優，改進算法兼顧了系統調節時間以及抗擾性能。

表3 控制指標對比

4 結論

提出的改進ITGC算法，經理論分析和實驗驗證得出結論。

(1)改進算法對解決大時滯系統的控制提供了一種借鑒和參考。

(2)與經典PID、ITGC等對比，具有調節時間短以及抗擾性強的優勢。

(3)當由于系統時變性以及建模不準導致模型失配時，算法依然適用。

(4)改進算法易于編程，實物驗證控制效果與仿真一致。

(5)從圖解和公式說明了算法原理及具有優勢的原因，為算法投運提供理論基礎。算法的設計為大時滯系統的控制提供了新的解決途徑。