關節式雙履帶移動機器人越障穩定性分析

宗成國，劉紀新，于 巖，徐丕兵

(1.青島黃海學院智能制造學院，青島 266427；2.山東科技大學機械電子工程學院青島 266510；3.青島市技師學院軌道交通學院, 青島 266229)

履帶式移動機器人作為一種對非結構環境探索的智能化設備，可以輔助工作人員對非結構環境進行遠距離的偵測與探查工作，降低事故的發生率[1-2]。

目前，國內外研究學者在履帶式移動機器人相關領域做了大量研究工作。美國在該領域的研究走在了世界的前列，IRobot公司研制的Packbot機器人是一種用于城市建筑物救援的微小型履帶式移動機器人，該機器人前端安裝兩擺臂，可有效提高機器人的越障能力[3]；德國Telerob公司研制的Teodor機器人是一款用于排爆的履帶式移動機器人，該機器人已多次應用于反恐演習中[4]。中國也在開展履帶式移動機器人的研究工作，哈爾濱工業大學研制了一種用于煤礦井下探測的六履帶移動機器人，該機器人可對井下巷道的環境進行檢測[5]；北京航空航天大學研制了一種可重組的履帶式移動機器人，該機器人具有較強的爬樓梯能力[6]。

以上所提及的履帶式移動機器人可分為雙履帶移動機器人、四履帶移動機器人、六履帶移動機器人三種[7-9]。雙履帶移動機器人的特點是結構簡潔緊湊，可實現輕量化，但與四履帶移動機器人和六履帶移動機器人相比，其越障穩定性較差。因此，如何保證雙履帶移動機器人既具有較強的越障穩定性能，又結構簡潔緊湊，則是履帶式移動機器人領域急需解決的一個熱點和難點問題[10-14]。

擬設計一種基于非結構環境的關節式雙履帶移動機器人，該機器人平臺可由前、后殼體組成，在旋轉關節的作用下，該機器人將實現同四履帶機器人一樣跨越障礙物；此外，由于履帶的周長是固定不變的，此狀態下機器人的履帶會變松，容易引起打滑或脫落，為解決這一問題，提出一種履帶壓緊裝置，該裝置可實現機器人在工作中根據履帶形狀伺服壓緊履帶。在此研究基礎上，將以攀越二維崎嶇地形、正斜坡地形以及樓梯三種典型地形為例，對關節式雙履帶移動機器人的越障穩定性能進行相應的分析。最后，通過相關實驗來證明關節式雙履帶移動機器人的機構設計合理性和可行性。

1 機器人整體結構設計

履帶式移動機器人適合在復雜地形的環境下進行作業。這類機器人除進行正常形式的前向、后向和旋轉的基本動作外，還要具備攀越障礙物及攀爬樓梯的能力。所以，履帶移動機器人在非結構化環境下的運動穩定性的提高是機器人實現自身穩定運行的前提和保證。

結合上述分析，一種基于探索非結構環境的關節式雙履帶移動機器人便應運而生了，該機器人平臺由前殼體、后殼體、兩條履帶、六個履帶輪、一個關節電機、兩個驅動電機、兩套履帶壓緊裝置、一套無線通信裝置和一套電路控制系統組成，如圖1所示。后殼體的尾部位置安裝有兩驅動電機；前、后兩殼體相接觸的位置安裝有用于調整機器人姿態的關節電機，控制系統會根據傳感器所檢測到的信息控制前殼體繞關節軸旋轉相應的角度，機器人便可順利實現越障或攀爬樓梯。機器人平臺的后殼體內安裝有控制系統以及蓄電池，前殼體內安裝有無線通信裝置。

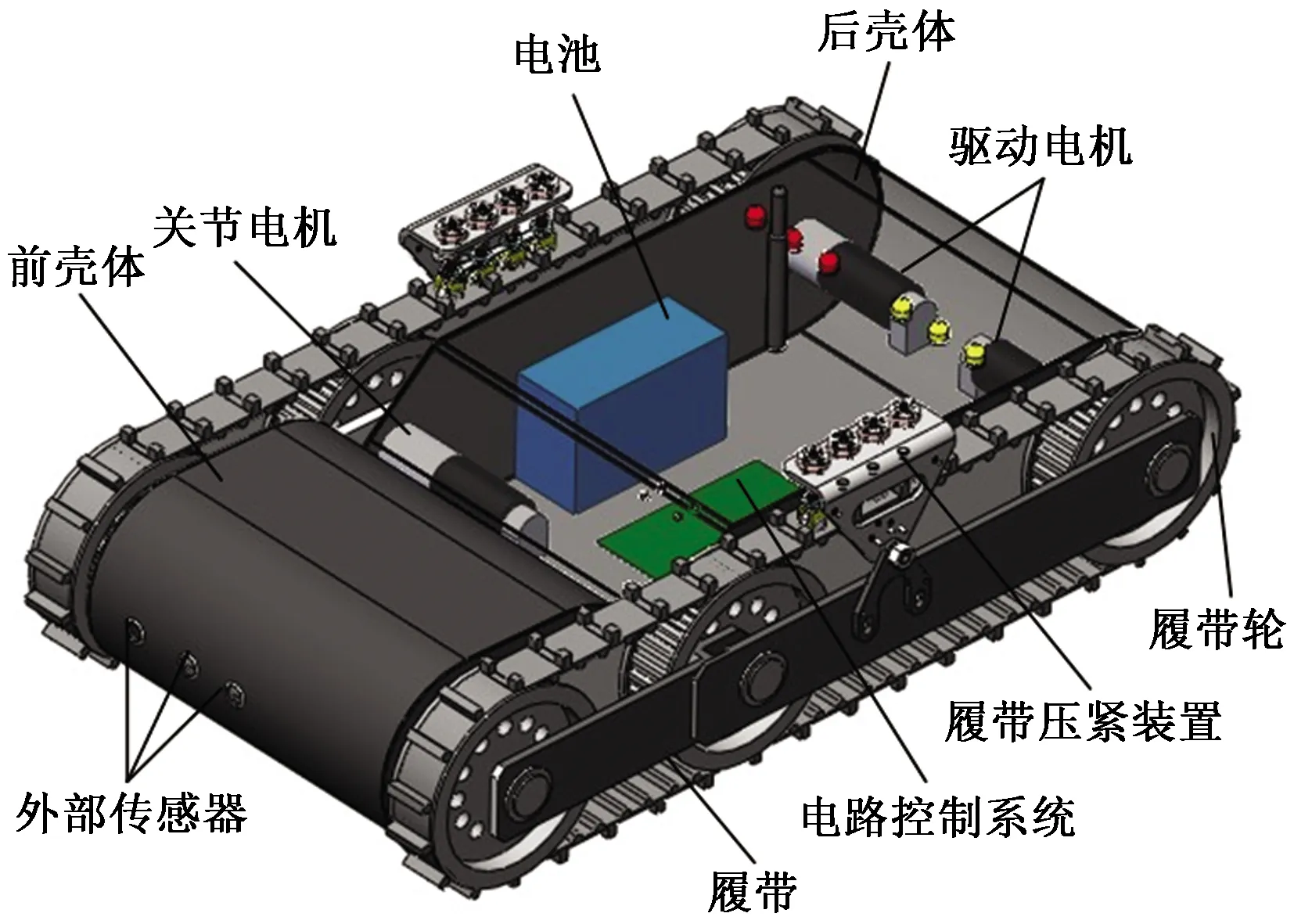
圖1 機器人總體機構示意圖

2 機器人越障穩定性分析

2.1 二維崎嶇地形的越障穩定性分析

如果機器人在水平面行駛的過程中碰到小石頭或經過凹凸不平的地面時，前殼體部分通過關節式電機驅動，可以繞關節軸抬升相應的角度，在這種情況下，機器人的前、后殼體會有某種角度的形成，這便增強了機器人翻越障礙物的性能。這時機器人整機的質心狀態如圖2所示，通過建立XCY坐標系，以機器人整機后殼體的質心C為原點，以X軸作為水平線，Y軸為其水平線經過坐標原點法線的方向，以D點作為機器人整機的前殼體部分的質心，當機器人整體在運動的過程中，質心Z坐標處于恒定狀態，即Lz≡0。利用其質心坐標的公式Z(Gx,Gy)能夠推算出機器人整機質心坐標如下：

(1)

式(1)中：α為前殼體部分的擺角；m1為后殼體部分的質量；m2為前殼體部分的質量；L1為后殼體部分長度；L2為前殼體部分長度。

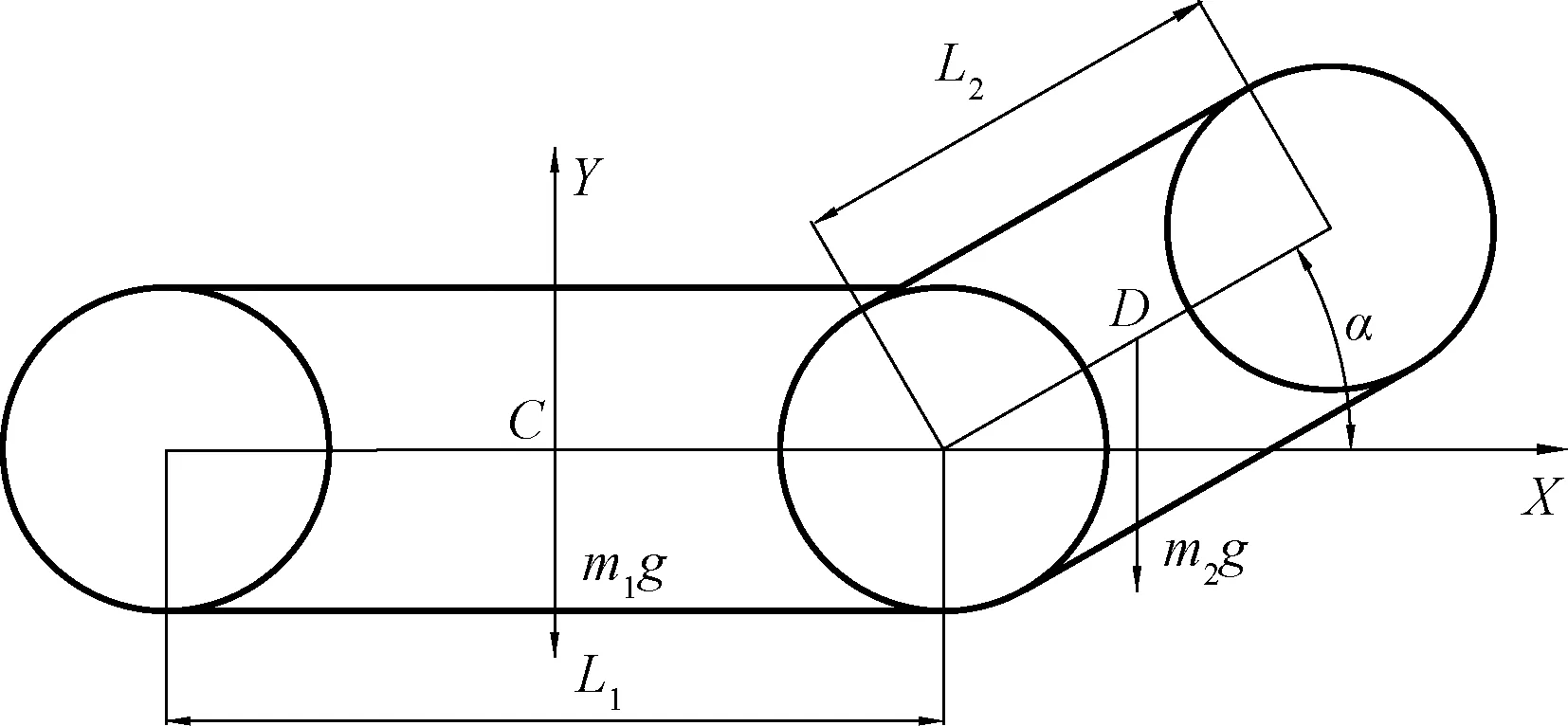
圖2 二維復雜地形的機器人結構的質心狀態

取機器人整體的前、后殼體部分的質心點，假定全部處于其各自的幾何的中心位置，令機器人整體的質量m=m1+m2，式(1)可作如下變換:

(2)

通過上述分析可得，當前殼體部分的擺角α發生變化時，機器人的質心波動的范圍是以[m2L1/(2m),0]為圓心，m2L2/(2m)作為其半徑的圓上。通過式(2)得知，當其滿足剛性條件時，若減小m2/m的值和前殼體部分的質心半徑L2/2，可以讓機器人整體的質心波動得到進一步減小，提高機器人整體在翻越二維復雜地形時的靜態特性。

當機器人翻越障礙物時，前殼體部分的擺角α的擺動范圍設置為(-π/4,π/4)，可以得到質心Z(Gx,Gy)的波動范圍如下：

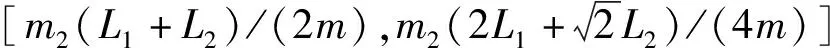
(3)

(4)

提出的雙履帶關節式可動式機器人整體的質量結構數據為：m1=20 kg，m2=8 kg，L1=450 mm，L2=200 mm，α∈(-π/4,π/4)。圖3顯示了機器人整機的質心坐標Gx、Gy隨著前殼體部分的擺角α變化的狀態分布。通過圖3(a)可知，當α∈(-π/4,π/4)時，機器人整體的質心橫坐標可以取到其最大值，當α∈(-π/4,π/4)或α∈(-π/4,π/4)時，質心的橫坐標部分可以取得其最小值，在α∈(-π/4,π/4)變化范圍內，質心的橫坐標變化的曲線取作拋物線。通過圖3(b)可知，當α=-π/4時，機器人的質心縱坐標可以取得其最小值部分，當α=π/4時，質心的縱坐標可以取得其最大值，在α∈(-π/4,π/4)變化范圍內，質心的縱坐標和前殼體部分的擺角呈現出線性變化的關系，前殼體部分的擺角相對于質心的縱坐標部分影響偏大。

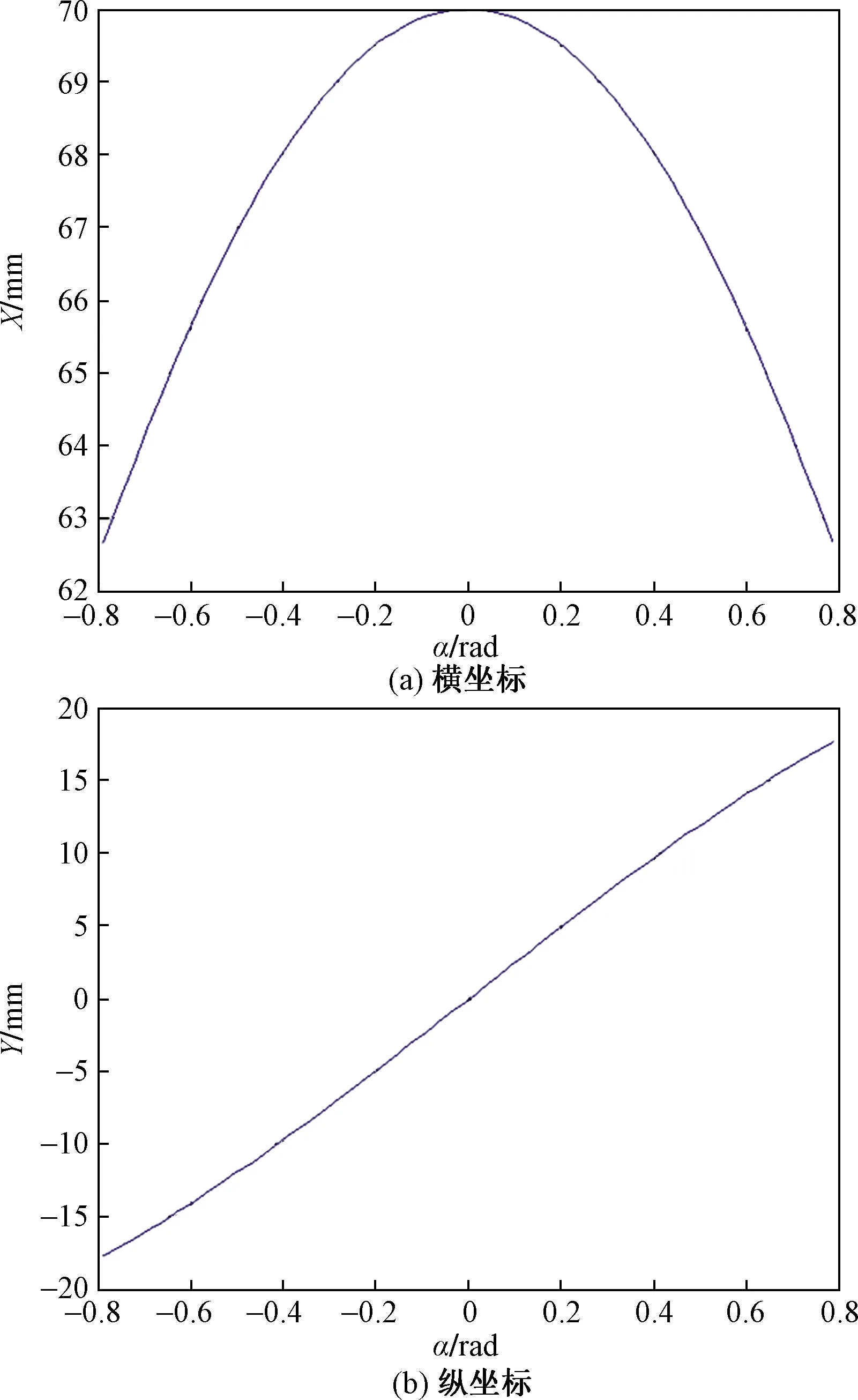
圖3 質心的橫縱坐標隨m1=20 kg變化的分布

2.2 正斜坡的越障穩定性分析

當機器人在正斜坡的地形上動作時，機器人會繞著Y軸進行旋轉某β角，如圖4所示，如果斜坡面上沒有各類阻礙機器人運動的物體，則機器人整機在這種地形上動作時，可以將質心的Z坐標認定為恒定不變，即G′z≡0。通過質心坐標的公式可以得到機器人平臺的質心Z(G′x,G′y)的坐標為

(5)

式(5)中：β為斜坡坡度，令m=m1+m2，式(3)可變換為

(6)

當機器人攀越正斜坡時，前殼體部分擺角α的波動范圍設置為(0,π/4)，由此可得質心Z(G′x,G′y)的波動范圍為

(7)

G′y∈[0,m2L2/(2m)]

(8)

圖4 機器人攀越正斜坡地形

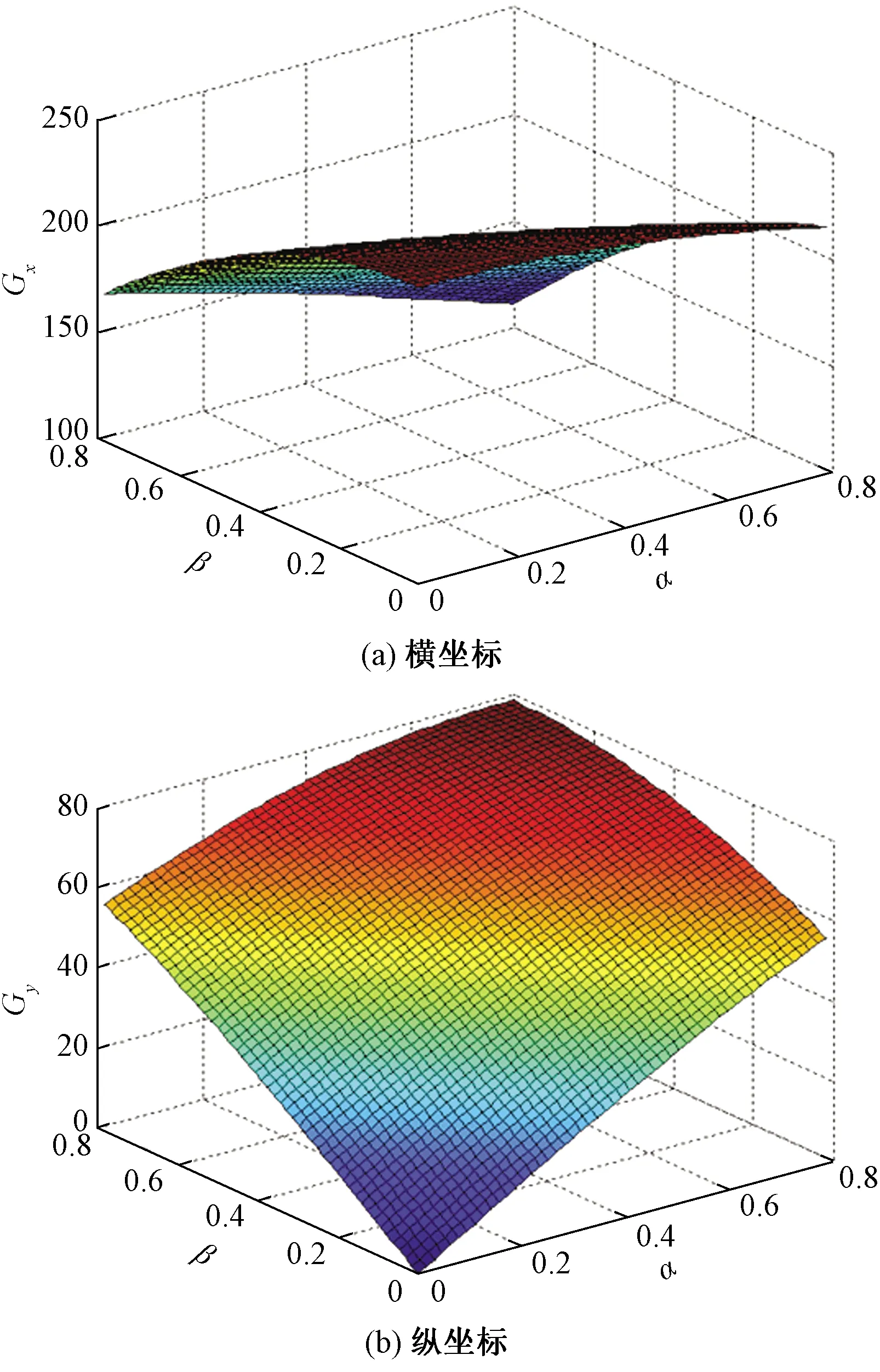
圖5 質心的橫縱坐標隨α、β的分布

圖6 機器人攀越樓梯發生側翻臨界狀態

圖5所示為機器人整體的質心的坐標G′x、G′y隨著前殼體部分的擺角α、斜坡角β波動的狀態分布。可知，如果前殼體部分的擺角α∈(0,π/4)，并且當斜坡角β∈(0,π/4)時，質心的橫坐標G′x的波動比較小，質心的縱坐標G′y波動則偏大，可以減小m2/m和前殼體部分的質心旋轉的半徑L2/2，來改善機器人整體在斜坡上運行的穩定特性。

2.3 攀越樓梯臺階的越障穩定性分析

當機器人在爬樓梯臺階的過程中，開始階段容易產生側翻，如圖6所示，若機器人在位于產生側翻的臨界點時，其后殼體部分和樓梯臺階的邊緣接觸的地方所產生的支反力是0，在這種情況下，機器人會和與地面碰撞的履帶輪的支撐線為軸線產生側翻，由圖6所示的關系得出，機器人產生側翻時的與樓梯臺階的坡角δ為

(9)

把式(1)代入式(7)，得出：

(10)

結合式(8)，可知機器人整體運動時在剛剛爬樓梯臺階時產生失去穩定性而發生側翻的表達式為

(11)

通過上述分析，如果要讓機器人整體在翻越樓梯的過程中不發生側翻，必須保證F(α,δ)<0，因此有必要減小前殼體部分的重量在機器人整體的重量中所占的比重，也就是m2/m的比值，和前殼體部分的質心旋轉半徑L2/2，加大后殼體部分的長度L1。

3 實驗分析

為了證實上述所設計的機器人整體的運動學模型分析理論的可靠性，履帶式機器人在樓梯臺階、正斜坡以及二維復雜地形上的靜態穩定特性以及越障性能的可行性，以設計的雙履帶關節式可動式機器人作為實驗平臺，以攀越樓梯為例開展機器人的越障實驗。通過爬樓梯越障實驗來證明雙履帶關節式可動式機器人復雜地形的通過性、攀越障礙的可靠性和理論研究的正確性。

圖7 機器人翻越樓梯實驗

通過圖7實驗表明，機器人跨越障礙的穩定性能比較好，結構具有緊湊性，便于攜帶及使用，以及被動調節裝置具有非常好的壓帶功效。

4 結論

(1)設計的關節式雙履帶移動機器人具備較高攀越障礙的能力，通過實驗證明，該機器人具備較強的環境適應性和越障性能。

(2)對機器人攀越二維崎嶇地形、正斜坡，以及攀爬樓梯的越障穩定性進行了理論分析，建立了數學模型，實驗驗證了機器人在越障時具有較高的穩定性。

(3)對機器人攀越障礙的穩定性進行了理論分析，通過實驗證明了理論分析的正確性，為研究探索非結構環境機器人提供了參考依據。