基于改進TEB算法的阿克曼機器人運動規劃系統
鄭凱林,韓寶玲,王新達
(北京理工大學機械與車輛學院,北京 100081)
移動機器人的路徑規劃分為全局路徑規劃和局部路徑規劃。全局路徑規劃負責在全局地圖尋找一條從起點到終點無碰撞的路徑,但一般不具有實時更新路徑動態避障而且滿足運動學動力學約束的特點。局部路徑規劃起到修飾全局路徑,動態更新調整路徑避開動態障礙物的作用,機器人局部路徑規劃中常見的算法有動態窗口法[1],在可行的速度采樣空間[v,w],模擬在未來時間段機器人可以達到的軌跡集合。設置評價函數評估軌跡的代價,選擇代價最小的軌跡對應的速度發送給機器人底盤。該方法適用于全向移動和差速機器人,不適用阿克曼轉向幾何約束的機器人。廣東工業大學徐寶來等提出了適用阿克曼機器人的改進動態窗口法,將線速度角速度采樣空間[v,w]替換成線速度虛擬轉向角空間[v,α][2],軌跡的優劣受采樣的分辨率和評價函數的參數有關,而且控制動作在預測范圍內保持不變。人工勢場法[3]也是廣泛應用在機器人局部路徑規劃上[4],但是機器人容易陷入障礙物斥力函數和目標點引力函數平衡而造成目標點不可達。燕山大學王洪斌等提出增設虛擬子目標的方法解決局部極小值問題,利用自適應步長調節算法對移動機器人的步長進行了動態優化[5]。改進的人工勢場法都是為了機器人避開障礙物脫困,并無對具有非完整約束的阿克曼機器人運動學和動力學的考慮。Rosmann等提出了TEB算法[6],該算法將傳統的運動規劃問題表述為一個圖優化問題,可以適用于完整約束和非完整約束機器人[7],后又針對阿克曼機器人進行了擴充支持[8],由牛頓第二定律可知,加速度反映在加速度運動時受到的力,加加速度則反映這作用力的變化快慢。較大的加加速度將會產生沖擊感,例如在電梯升降,汽車、飛機等加速和轉彎的過程中。
對于機器人而言,缺少對加加速度的約束,電機輸出力矩短時間產生較大范圍突變會對阿克曼機器人產生沖擊震蕩。在此研究基礎上,現在多目標優化問題約束上構建加加速度約束,使動力學約束更加完善,并將該算法應用在阿克曼機器人運動規劃上,進行了仿真和真實機器人實驗。將從阿克曼機器人運動學模型構建、TEB算法模型構建和求解優化改進、導航框架設計、仿真和真實機器人測試等方面進行論述。
1 阿克曼機器人運動模型構建
機器人運動規劃需要建立機器人的運動學模型,在世界坐標下對阿克曼機器人構型描述如圖1所示。
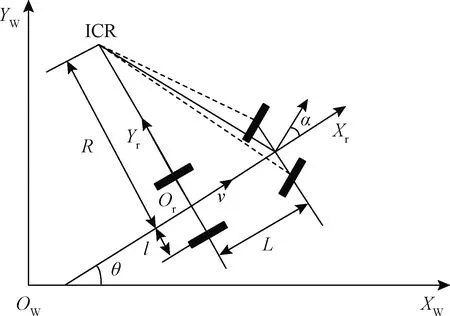
圖1 阿克曼機器人在世界坐標系的構型
世界坐標系為OWXWYW,機器人的基坐標系設置在機器人后軸中心Or上,ICR是阿克曼機器人的瞬時旋轉中心,后軸速度為v,機器人的前輪虛擬轉向角α,方向角為θ,機器人的轉彎半徑為R,機器人前后軸軸距為L, 后輪兩輪距為2l。其中轉彎半徑R與軸距和前輪虛擬轉向角α有關,不能無限小,需滿足:
R=L/tan[α(t)]
(1)
w=v(t)/R
(2)
式中:w為機器人后軸角速度。
阿克曼機器人運動學狀態方程建立如下:
(3)

(4)
阿克曼機器人的控制輸入量u(t)=[v(t),α(t)]T,虛擬轉向角α(t)因為阿克曼轉向幾何機構[9]存在一個范圍。
2 TEB算法模型構建以及改進約束
2.1 TEB軌跡模型構建
TEB將機器人的一系列位姿軌跡模型抽象成帶有時間信息的彈性帶模型。機器人的第i個位姿狀態可以表示為si=[xi,yi,θi],位姿包含位置信息xi、yi和方向角θi。ΔTi是機器人位姿si和si+1的過渡時間間隔。TEB的軌跡序列可以表示為如圖2所示。
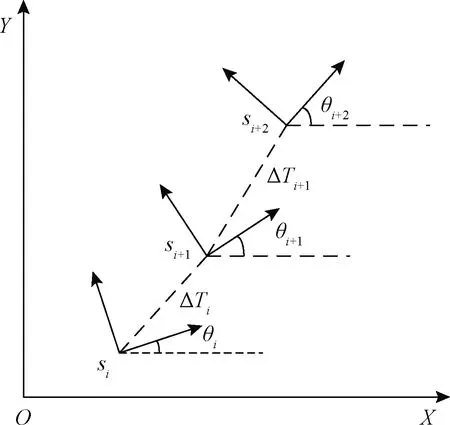
圖2 機器人在世界坐標系下的軌跡序列
機器人在世界坐標系XOY下的位姿序列可以表示為
C={si},i=0,1,…,n;n∈N
(5)
TEB描述的軌跡模型的位姿si到si+1的時間間隔為ΔTi,n個位姿間隔的時間序列為
Δτ={ΔTi},i=0,1,…,n-1
(6)
每個時間間隔表示機器人從一個位姿運動到另一個位姿的時間。TEB軌跡模型包含位姿序列信息和時間間隔序列信息,軌跡信息可以表示為
T:=(C,Δτ)
(7)
TEB算法存在的約束目標如下:
2.2.1 避開障礙物
機器人的軌跡是必須滿足避開障礙物[10]。機器人的距離與障礙物的距離為d,機器人與障礙物的允許距離為dmin,障礙物根據環境動態更新,障礙物的位置可以通過激光雷達獲取,在代價地圖上讀取障礙物的位置。對于每個位姿,可能受n個障礙物影響,需要考慮對某個位姿的n個障礙物影響。當障礙物超過機器人與障礙物允許的最小距離時,約束函數的值為0。當機器人與障礙物的距離小于限制的距離,障礙物約束函數才起作用。約束函數如下:

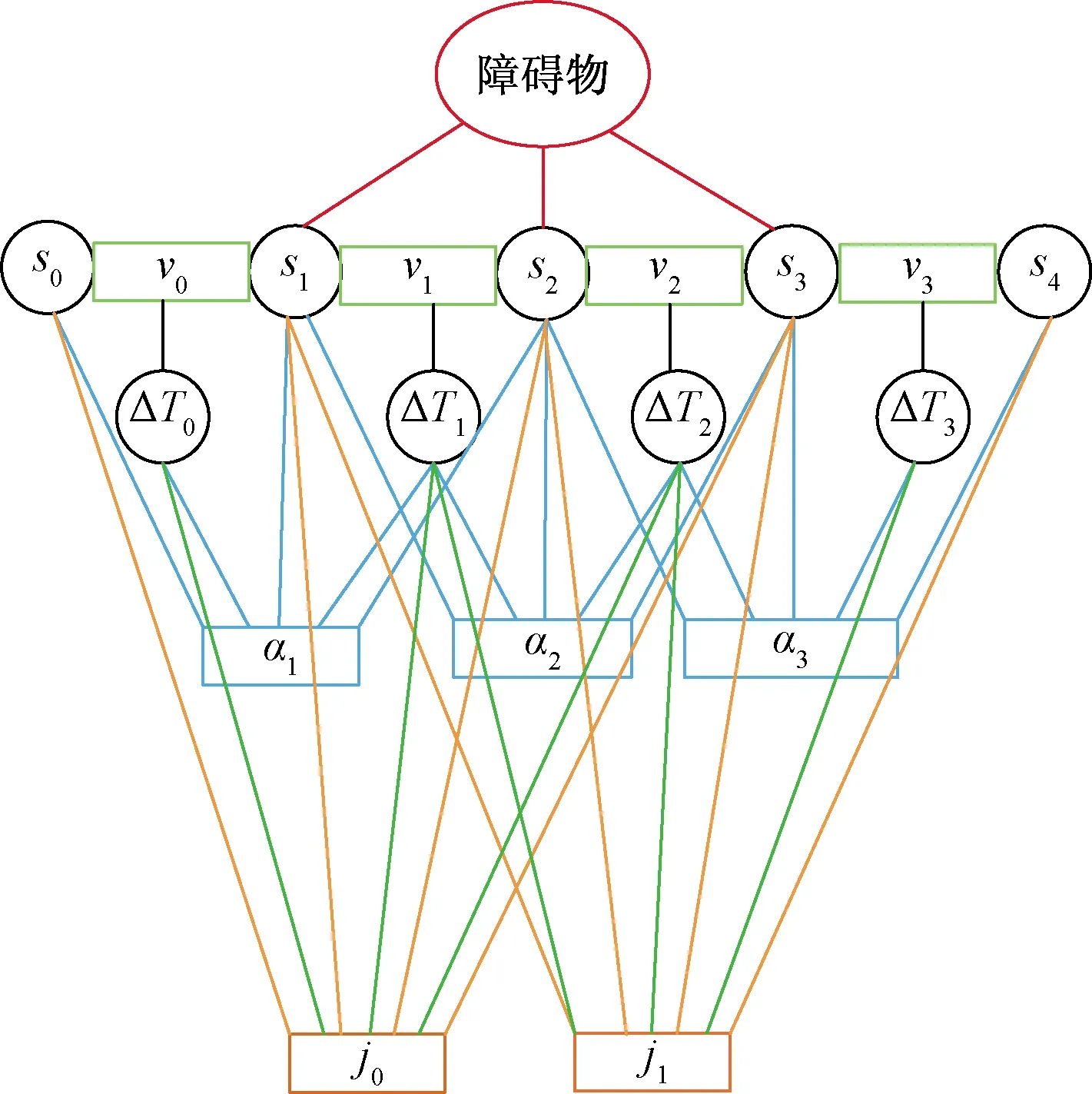
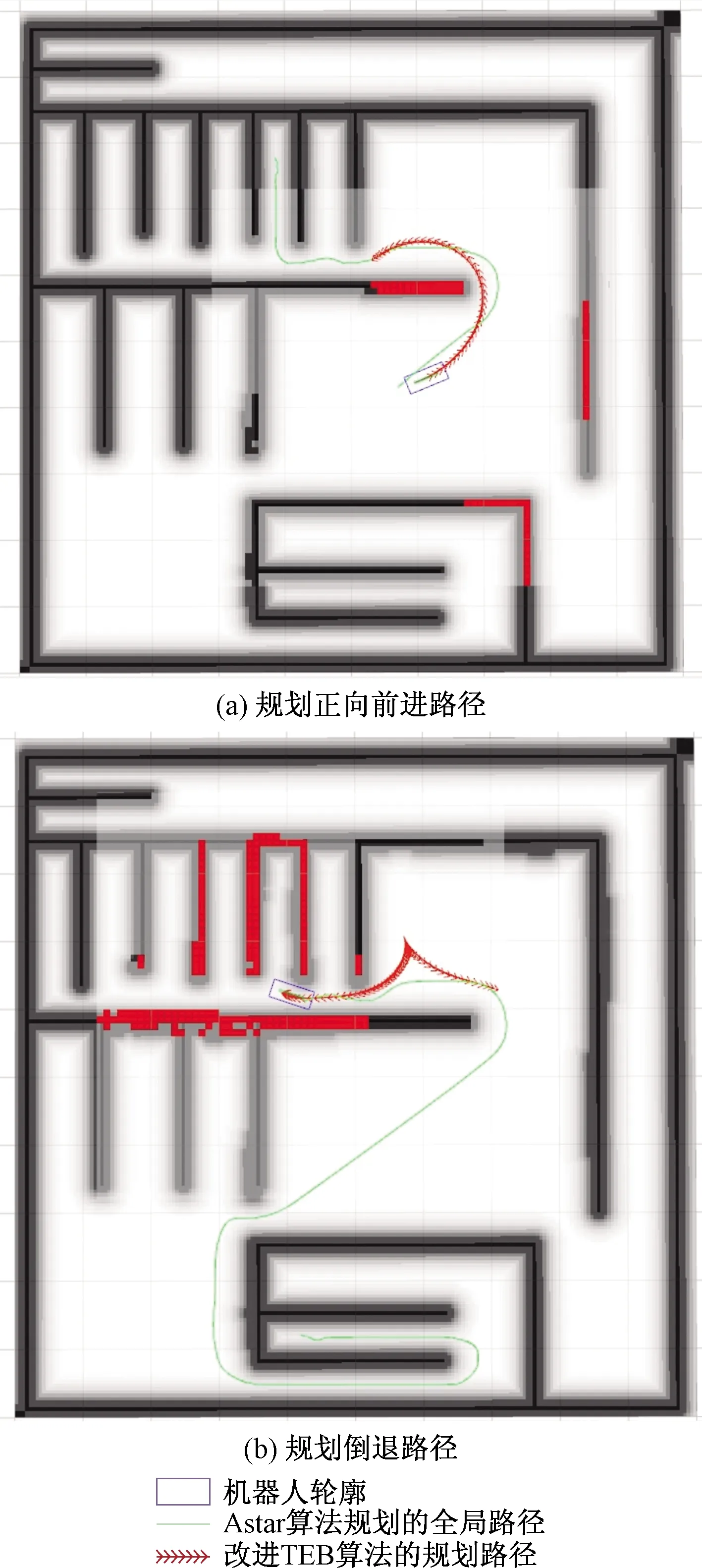
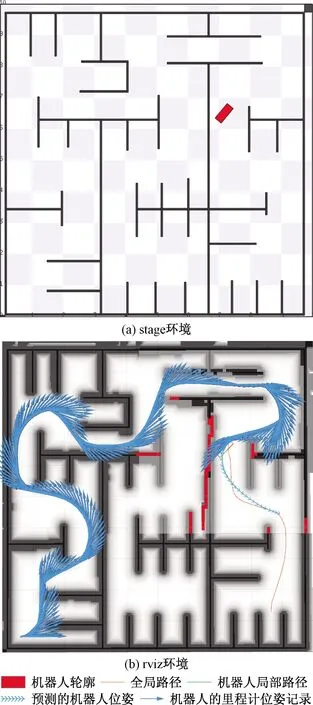
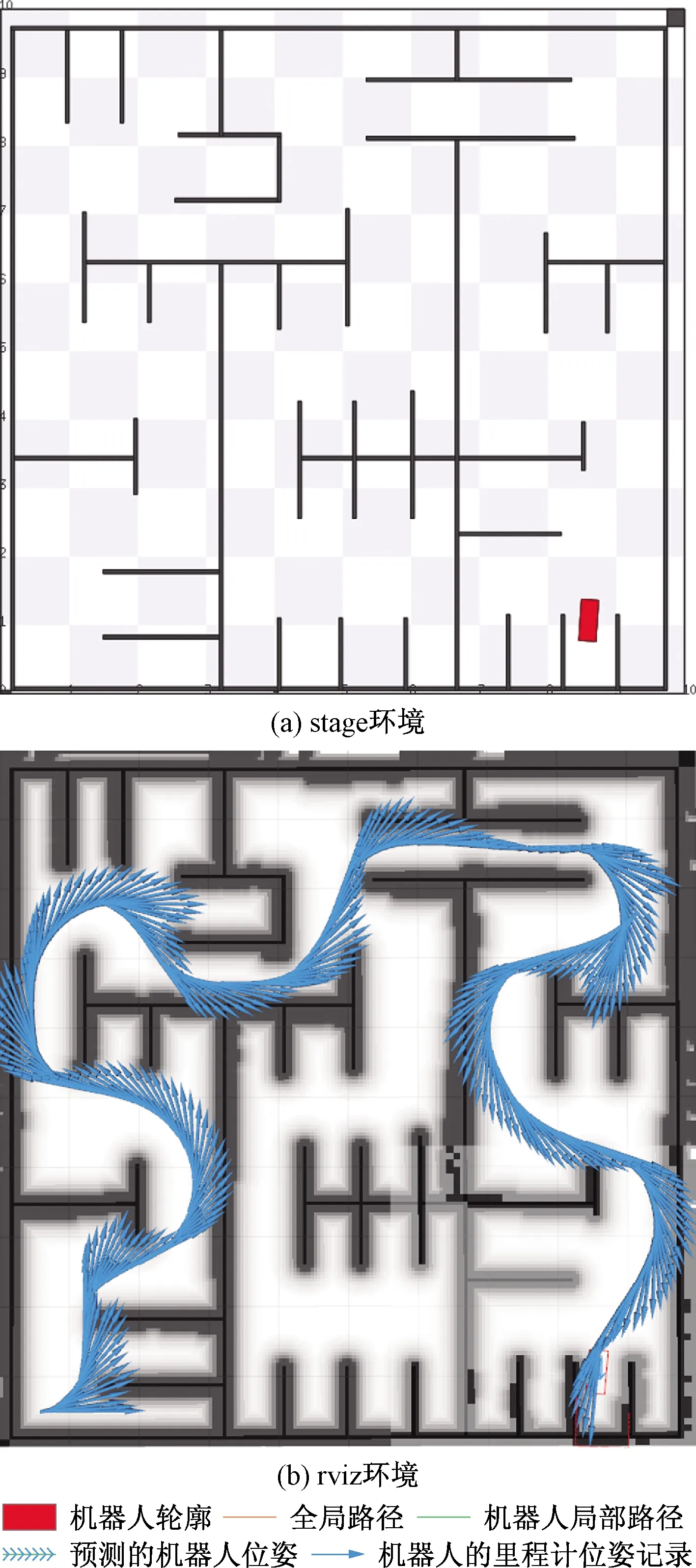
d (8) 2.1.2 速度和加速度約束 機器人速度和加速度的動態約束通過類似的懲罰函數來描述幾何約束。平均平移和旋轉速度分別根據歐式距離和方向角的改變量計算,在兩個連續的位姿xi、xi+1和兩個姿勢之間的過渡的時間間隔ΔTi[11]。 線速度: (9) 角速度: wi?(θi+1-θi)/ΔTi (10) 線加速度: ai?2(vi+1-vi)/(ΔTi+ΔTi+1) (11) 角加速度: αi=2(wi+1-wi)/(ΔTi+ΔTi+1) (12) 2.1.3 非完整運動學約束 非完整約束機器人相鄰的兩個位姿移動可近似為曲率不變的弧線運動[12]。阿克曼機器人以恒定速率轉彎如圖3所示。 圖3 阿克曼機器人轉彎示意圖 機器人的位姿狀態由si運動到si + 1,機器人做圓周運動,si和si+1都落在曲率不變的圓弧上,其中滿足: βi ,i=βi ,i + 1 (13) (14) (15) 式(15)中:θi和θi+1機器人在世界坐標系的方向角,非完整約束的代價函數表示為 (16) 阿克曼機器人的轉彎半徑必須大于等于最小轉彎半徑 (17) 2.1.4 最短時間的目標函數約束 最快時間是考慮TEB全局性,因為目標函數需要依賴于所有的參數。是通過最小化所有時間間隔之和的平方要求機器人盡可能快地到達規劃的終點。最短時間約束函數可表示為 (18) TEB的核心思想是求解出一系列這樣的最優的帶有時間間隔的機器人位姿序列。目標函數的大部分位姿是局部的,因為它們僅取決于少數幾個連續位姿的數量,而不是整條全局軌跡上的位姿。TEB的局部性導致稀疏系統矩陣的產生,可以使用專用的快速有效的大規模數值優化方法[13]求解。關鍵思想是通過調整位姿和時間間隔來優化TEB,使用權重求和模型求解多目標優化問題。通過構建多目標優化得到最優的位姿和時間間隔。 (19) T*=argTminf(T) (20) 式中:T*表示優化的TEB結果;γk是函數k的權重系數;f(T)表示各種約束目標函數之和,它是各目標函數乘以權重系數的和。TEB優化問題[式(18)]可以轉化為hyper-graph(超圖)問題,所謂 的超圖是其中一條邊的連接節點不受限制。因此,一條邊可以連接兩個以上的節點。TEB求解問題能夠轉換成以位姿和時間間隔為節點的超圖。節點之間通過給定的目標函數 相連。圖4顯示了位姿、時間間隔、速度、加速度之間的連接關系。速度約束目標函數需要知道兩個位姿歐式距離之差和時間間隔,因此,它形成了一條連接機器人位姿和時間間隔的邊。同理,加速度約束函數也是這樣。障礙物需要一條邊連接到能影響機器人的幾個位姿。代表障礙物的橢圓節點是無法優化的。根據位姿,時間間隔、速度、加速度以及障礙物構建出的超圖如4所示。 圖4 超圖 解決具有硬約束的非線性問題在計算代價非常大。因此,提高效率快速在線求解一直是非線性研究的重點。非線性問題轉化為近似非線性平方優化問題,當求解器利用問題的稀疏模式時,它通過一階導數逼近Hessian矩陣,從而有效地解決了該問題。約束作為懲罰項納入目標函數[8]。 為了求解方程利用LevenbergMarquardt(LM)方法,因為它兼顧魯棒性和效率。圖優化框架g2o[14]實現LM的高效稀疏變量求解方程[式(20)]。 TEB以一定的頻率進行重復求解,這個頻率高于機器人的響應控制周期。在每個軌跡修正步驟中,TEB算法都會動態添加新的位姿和刪除以前的位姿,為了將時空分辨率調整剩余的軌跡長度或規劃范圍。對于實時更新的障礙物,TEB在優化的那一時刻當作靜態障礙物來處理。g2o框架批量優化了TEB軌跡,因此每次迭代都會生成一個新圖。在單個機器人控制周期內,每個循環進行多次循環迭代求解。在每個采樣周期中,控制輸入量u(t)從優化的軌跡中得到。TEB算法流程如下: 1輸入全局路徑,給定機器人的起始位姿和終點位姿;2截取一段全局路徑,獲得初始化軌跡(包含機器人位姿和默認時間間隔),構建多目標優化問題;3進入迭代求解循環4 調節修剪局部軌跡長度,維持局部優化的軌跡長度不變,刪除機器人走過的固定長度的軌跡;5 更新代價地圖中的障礙物信息;6 建立hyper-graph(超圖)進行多次迭代求解出最優軌跡列;7 檢查軌跡是否可行;8 將式(19)B?映射到u(t),根據相鄰的軌跡點計算出控制量信息包括后軸速度和前輪虛擬轉向角;9 到達終點,結束算法; 得到優化的TEB軌跡之后,控制變量速度v和阿克曼機器人的虛擬轉角α可以計算出來下發給機器人驅動器。在每次新迭代之前,重新初始化階段都會檢查新的和更改的位姿點。 在機器人的運動過程中,加速度約束能保證速度變化率不會太大。加速度的變化率過大會對機器人造成沖擊。增加加加速度約束,將加加速度的變化率限定在一個較小的范圍,提高機器人運動的平順性以及提高電機的壽命,現將加加速度約束添加到超圖中,構建新的超圖。j0這條邊連接到這三個ΔT0、ΔT1、ΔT2這三個時間間隔頂點和s0、s1、s2、s3這四個位姿頂點,j1連接的時間間隔和位姿數量不變,分別往后順延一個序號,如圖4所示: 圖5 改進的超圖 s0、s1、s2、s3、s4是機器人連續的5個位姿狀態,v0、v1、v2、v3是連接上述5個位姿的速度狀態(包含線速度和角速度),a0、a1、a2是加速度狀態(包含線加速度和角加速度),j0、j1滿足的加加速度約束關系如下: 線加加速度可表示為 j0lin=(a1lin-a0lin)/(0.25ΔT0+0.5ΔT1+ 0.25ΔT2) (21) 角加加速度可表示為 j0rot=(a1rot-a0rot)/(0.25ΔT0+0.5ΔT1+ 0.25ΔT2) (22) 在程序實現過程中需要重新給g2o庫定義加加速度邊作為約束條件和添加加加速度約束。在局部規劃起始狀態和中間狀態以及終點狀態中分別應用。 整個運動規劃框架的設計基于機器人ROS系統,利用ROS的通信機制進行通信[15]。利用開源的move_base充當決策層提供action通信機制,給定一個全局導航目標點,調用Astar全局路徑規劃器生成全局路徑,全局規劃器發布全局路徑給局部路徑進行路徑規劃,計算控制指令下發給機器人底盤。move_base節點將全局和局部路徑規劃程序通過狀態機連接在一起,以完成導航任務,還維護兩個用于完成導航任務的代價地圖,一個用于全局規劃程序,一個用于局部路徑規劃程序。整個框架設計如圖6所示。 move-base狀態機分為planning,controlling,clearing三種狀態。planning是接受新目標與進行全局規劃的整個過程,controlling是進行局部路徑規劃發出速度指令的行為,clearing是全局規劃和局部規劃失敗或困住觸發recovery行為的用來處理上述情況的異常。當move_base接收到目標終點請求,move_base調用makePlan函數進行全局規劃,便啟動Astar全局路徑規劃器,進行全局路徑規劃,規劃完成將全局路徑以話題通信的方式發布(publishPlan)出來,move_base狀態機切換到controlling狀態,改進的TEB路徑規劃器通過相關函數(setPlan)接收全局路徑,里程計負責定位,激光雷達獲得障礙物信息,以一定的頻率進行局部路徑規劃,計算出控制指令,發布給機器人下位機控制器。 仿真和實際實驗的對象是一個具備阿克曼轉向機構的非完整約束機器人。機器人的運動學參數:機器人前軸虛擬轉角限定范圍為[-30°,30°],軸距L=0.9 m,最小轉彎半徑1.56 m。 仿真平臺:stage。仿真計算機配置:CPU I7 主頻2.6 GHz,6核12線程,局部路徑規劃頻率為20 Hz。機器人參數如表1所示。 對權重參數調優后,搭建仿真環境進行測試。 仿真場景一:進狹窄巷道和機器人脫困 仿真分析:由圖7(a)可知能規劃出符合阿克曼機器人運動學的路徑,軌跡曲率符合要求。由圖7(b)可知該算法能規劃出調頭的路徑而且滿足阿克曼機器人的非完整約束和最小轉彎半徑約束。規劃的路徑符合仿真地圖的實際情形。 圖7 阿克曼機器人規劃局部路徑 仿真場景二:復雜迷宮地圖場景 仿真分析:由圖8、9可知,機器人能得到一條滿足阿克曼運動學動力學從起點到終點的一條無碰撞路徑。 圖8 機器人路徑規劃過程展示 圖9 路徑規劃結果展示 對配有16線激光雷達的真實機器人在封閉多墻體場景進行測試,測試的真實機器人如圖10、圖11所示。 圖10 機器人規劃過程 圖11 規劃結果精度測量 真車測試結果表明:阿克曼機器人能避開障礙物,能夠基本到達設定的目標點,位置平均偏差約6 cm,航向角平均偏差約8°。實驗次數設置為50次,在改進TEB算法之前,機器人受到明顯沖擊的次數為5次,概率為1/10,改進TEB算法后,添加加加速度約束后,整個導航過程中機器人沒有受到任何沖擊發生震蕩,運動過程非常平順,基本到達預期要求。 針對阿克曼機器人運動規劃問題,提出了一種改進的TEB算法,并得到如下結論。 (1)建立了阿克曼機器人運動控制模型。 (2)提出了一種改進TEB算法,將加加速度約束添加到TEB算法中,減少加速度突變帶來的沖擊,提高運動的平順性。 (3)將該改進算法在阿克曼機器人應用,并在stage仿真環境中實現,最終在真實機器人上進行了測試和應用。不僅驗證了改進的TEB算法的有效性,而且在阿克曼機器人上進行了有效應用。 該算法可廣泛應用于阿克曼機器人的局部路徑規劃中,也可廣泛用于自動駕駛汽車自動泊車領域。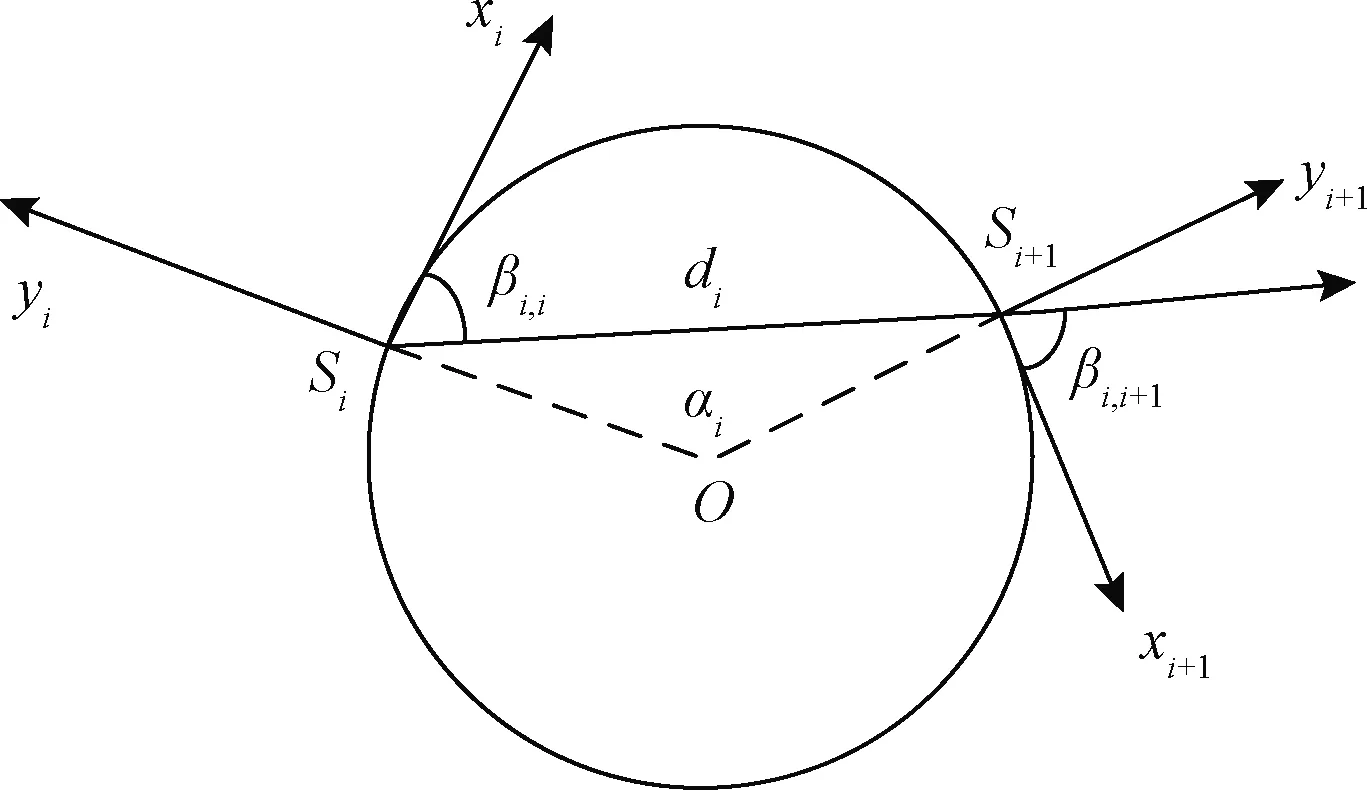
2.2 TEB算法求解模型的構建


2.3 改進TEB約束條件
3 阿克曼機器人運動規劃框架設計
4 仿真實驗和真車測試實驗
4.1 仿真實驗
4.1 真實機器人實驗


5 結論與展望

