基于格子Boltzmann方法的雙空化泡遠壁區潰滅規律研究
(四川大學水力學與山區河流開發保護國家重點實驗室 成都 四川 610065)
一、引言
空化現象由空化泡的初生、發育和潰滅過程組成,是一種氣液兩相之間質量傳輸的非定常可壓縮湍流流動過程。空化泡潰滅瞬間形成巨大壓強,易造成材料剝蝕從產生空化現象[1]。由于空化發生時周圍環境不同,空化也分成很多種類,尤其是水質狀況[2]、機械裝置[3]、熱力學效應[4]等的變化都會對空化產生較大影響。空化泡廣泛存在于水中,特別是泄洪洞,水輪機和其他水力設施及水力機械中。空化泡在潰滅時遇洞壁,水輪機葉片等等固體邊界時,會產生高溫高壓高速射流現象[5]。
區別于傳統宏觀數值方法,格子Boltzmann法(LBM)基于分子動力學理論,從分子統計觀點出發來求解宏觀變量。這類方法在多物理場耦合作用下以及多相流或復雜流運動下具有潛在優勢[6]。格子Boltzmann兩相流模型中最常用的有以下四種:顏色模型、贗勢(偽勢)模型、自由能模型和雙分布的He-Chen-Zhang模型。
一些學者已經采用格子Boltzmann兩相流模型對空化泡在近壁區的演化規律進行了研究。曾建邦等采用格子Boltzmann方法分布模擬了剪切流下和錐形凹坑中空化泡的生長,得到了與理論或實驗數據吻合較好的結果[7]。彭浩等[8]采用三維格子Boltzmann偽勢模型研究了空化泡在近壁區潰滅過程。但是,已有的研究中均沒有涉及到空化泡在遠壁區潰滅過程,本文采用格子Boltzmann偽勢模型對雙空化泡在遠壁區潰滅進行了詳細的研究。
二、數學模型
在格子Boltzmann單松弛碰撞模型中,離散的粒子分布函數f_i被使用來代替流體粒子的分布函數發生演變,方程如下:
(1)
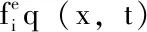
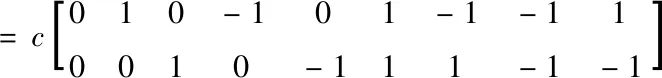
(2)
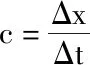
(3)
(4)
對應的宏觀控制方程可以表示為:
(5)
(6)
在LBM模型中,可以很方便的耦合外作用力將其加入到循環迭代當中。最常見的單組分多相流相互作用力Fi(x,t)為:
(7)
式中G是相互作用強度,ξi取值為ξi=1/9(i=2,3,4,5),ξi=1/36(i=6,7,8,9)。根據Yuan[50]的文章中提出的,相互作用勢可表示為:
(8)

C-S狀態方程的形式可以表示如下:
(9)
其中,參數公式如下:
(10)
(11)
臨界參數可表達如下:
(12)
(13)
在本文中,取a=1,b=4,R=1。
本文采用Kupershtokh[9]提出的準確差分外力格式消除了以前外力處理方式的誤差項,使得外力項可以完整的推導到平衡態分布函數,其演化方程表示為:
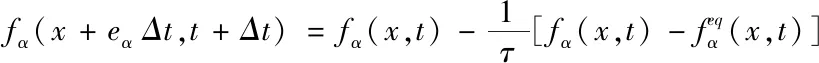
(14)
上式中出現的宏觀物理量計算公式為:
(15)
(16)
流體物理真實速度的計算公式為:
(17)
三、物理模型
為了獲得空化泡在遠壁處崩潰時可能產生的有用信息,構建的物理模型如圖1所示。四個邊界都為無窮大區域壁面.以水為環境介質。
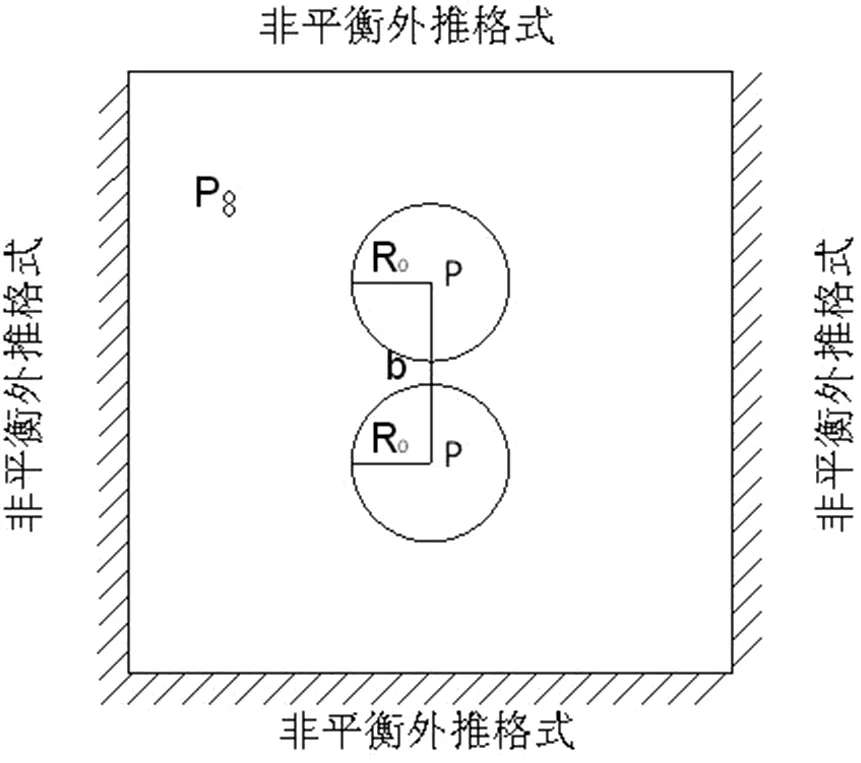
圖1 物理模型(R0—氣泡半徑; b—兩個空化泡中心的距離;
在接下來的雙空化泡在遠壁區潰滅演化規律的工作中,具體的模型設置如圖1所示:計算區域為401lu*401lu,鑒于模擬空化泡在遠壁區潰滅規律,數值模擬過程中要盡可能避免壁面對空化泡的影響,故四周使用非平衡外推格式。圖1中R0為氣泡半徑;b為兩個空化泡中心的距離;Pv為氣泡中的氣體壓強;P∞為液體壓強。模仿前面的研究,引進一個無量綱數λ。其中λ=(b-2R0)/R0,是表征兩個氣泡相對距離的量。在接下來的工作中,將探討不同的附加壓力P和不同的λ對遠壁區兩個空化泡相互作用潰滅的規律。從而全面的了解兩個空化泡在無窮大區域內潰滅的過程。
四、模擬結果
(一)低附加壓力下兩個空化泡在遠壁區潰滅
本次模擬了低附加壓力下兩空化泡相互作用潰滅的情況。此時P=0.0042,λ=0.2。如圖2所示,圖2(a)為50步時空化泡的密度場圖,兩個空化泡基本處于初始狀態。隨著模擬的進行,兩個空化泡在中心連線軸方向上拉長,原因是兩空化泡內部壓強低,互相吸引變化,類似于在兩個空化泡中間形成一個低壓區,變化猶如在兩個空化泡中間有一個壁面誘導其潰滅,通過圖2(b)可清楚地看到這些變化。到了圖2(c)時,兩個空化泡被拉長到一定程度后會在表面張力和周圍附加壓力共同作用之下向圓形變形。但是由于空化泡之間還存在低壓,相互吸引,因此對于上面的空化泡來說,底部變形速率變小,上部變形速率大。圖2(d)空化泡在表面張力、空化泡之間的相互吸引、外部壓力的共同作用之下由于上部和下部之間的壓強差相對于以前的壓力邊界來說變小,不足以將空化泡壓為月牙形,所以空化泡逐漸以半圓(球)形變小,最后潰滅。在本次研究中沒有發現二次潰滅。圖2(e)、圖2(f)為壓力場圖。
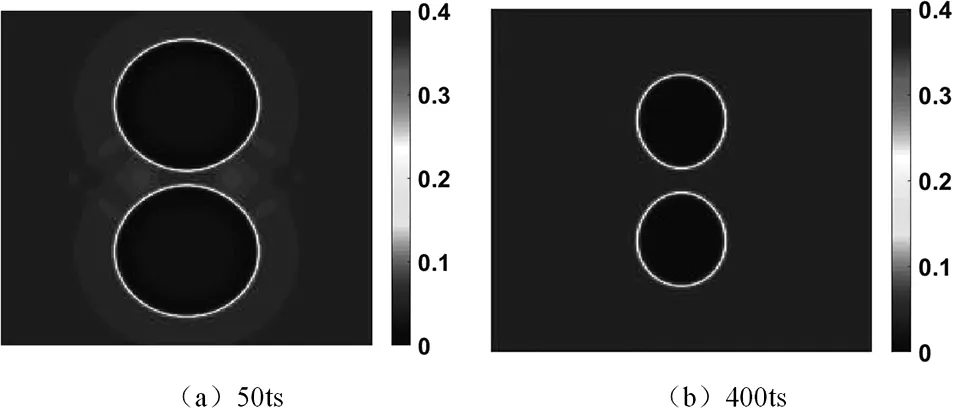

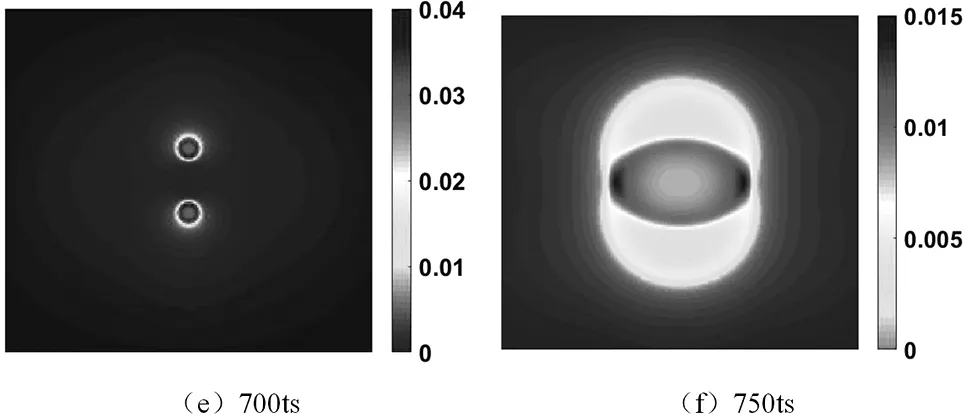
圖2 低附加壓力下兩個空化泡在遠壁區潰滅(P=0.0042,λ=0.2)
高附加壓力下兩個空化泡在遠壁區潰滅
為了更好地研究兩個空化泡在遠壁面潰滅情況,又對在保證模型穩定性前提下,對高附加壓力的情況進行了模擬研究,具體的模擬結果如圖3所示。


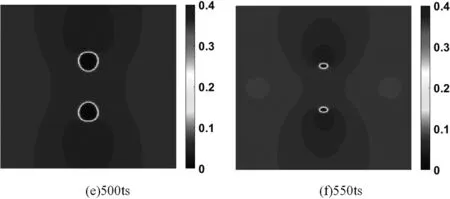
圖3 高附加壓力下兩個空化泡在遠壁區潰滅(P=0.0054,λ=0.2)
在本工況中,除了增大附加壓力外,其他條件均未改變。如圖所示:圖3(a)為初始設置,此時兩個空化泡處于圓形狀態。與上述工況相同,空化泡在相互作用下被壓縮變形呈橢圓形,如圖3(c)、圖3(d)。又由于表面張力作用變形,氣泡在附加壓力、空化泡間吸引力等綜合因素的影響下變為半圓形,如圖3(e)。此時由于附加壓力較大,空化泡有趨向于月牙形的趨勢,但空化泡間的低壓區較小,附加壓力與低壓區不足以形成擊穿空化泡的壓力差,空化泡最后并未出現月牙形。在模擬兩個空化泡相互作用潰滅的情況中,并未出現月牙形空化泡并被擊穿的現象。因此,兩個空化泡在遠壁區潰滅時很難出現空化泡被擊穿形成兩個空化泡然后發生二次潰滅的現象。
(二)兩個空化泡遠壁區潰滅時間隨附加壓力變化規律研究
在本節中,對兩個空化泡在遠壁區潰滅的時間進行了統計,可以清晰地看到在特定空化泡距離下空化泡潰滅隨附加壓力不同的變化,其變化趨勢呈現出規律化,具體的統計信息如圖4所示。
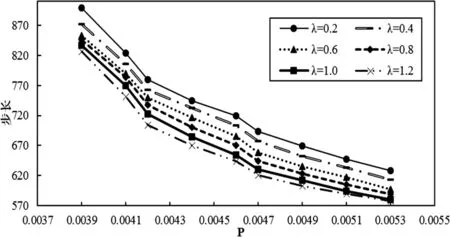
圖4 空化泡潰滅時間與附加壓力關系圖
通過圖4可以清楚的知道:隨著附加壓力的增大,空化泡的潰滅時間縮短,且當P>0.042之后,空化泡潰滅時間基本與附加壓力成線性關系。原因是空化泡潰滅的過程中由于附加壓力較小,氣相壓強和液相壓強在其特定的特征溫度下經過調整,有趨向于穩定的狀態,因而空化泡潰滅時間增長。而當附加壓力增大時,加上兩個空化泡之間會產生負壓呈現相互吸引的狀態,壓力場對空化泡作用充分,所以潰滅時間表現出規律性,潰滅時間與附加壓力之間的關系比較穩定。所以,兩個空化泡在遠壁區潰滅時間與附加壓力之間的關系已經基本探明,后面將統計在特定壓力下空化泡潰滅時間與不同距離之間的關系。
(三)兩個空化泡遠壁區潰滅時間隨空化泡之間距離變化規律研究
前面研究了空化泡潰滅時間隨不同的附加壓力的關系,下面統計了在特定的附加壓力下兩個空化泡潰滅時間隨不同的距離之間的關系圖,具體統計結果如圖5所示。
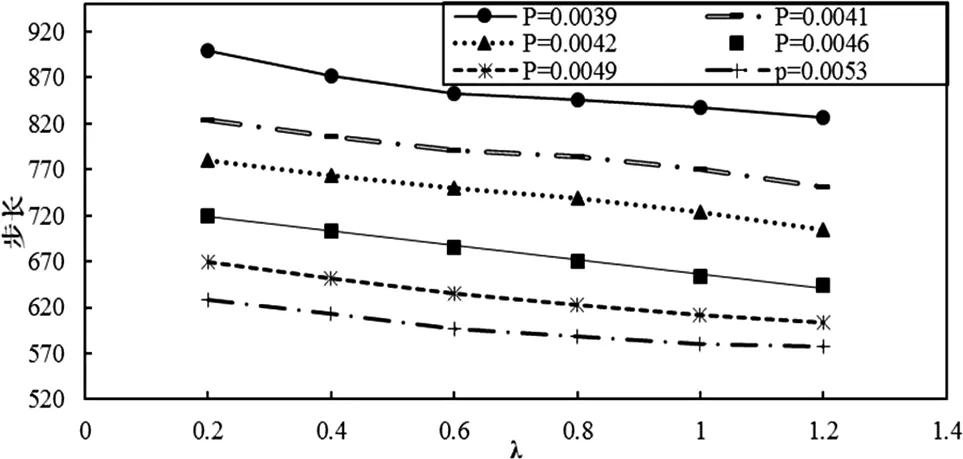
圖5 空化泡潰滅時間與相互之間距離關系圖
通過圖5可知:對于特定附加壓力下,空化泡潰滅時間與距離之間的關系基本呈線性,尤其是當λ>0.6后,潰滅時間與距離之間的關系呈現穩定的線性關系且時間變化很小,表明當兩個空化泡之間特征距離λ>0.6之后,兩個空化泡的相互作用對于空化發生已經基本沒有影響。而單個空化泡在近壁區潰滅規律中顯示當對于本研究中的特征距離等于空化泡半徑時時,壁面對空化泡潰滅的影響基本消失,比本次研究中的λ>0.6影響距離大,這是因為兩個空化泡在遠壁區潰滅雖然相當于中間有剛性壁面,但是兩個空化泡相互吸引力不如壁面的吸引大,所以在距離上呈現影響范圍小。
五、結論
在本文的研究中,采用LBM兩相流偽勢模型研究了兩個空化泡在無窮大區域內的潰滅演變規律,獲得以下結論:
1)空化泡相互吸引作用,對向潰滅,類似于在兩個空化泡之間有剛性壁面,兩個空化泡潰滅空化泡之間的低壓吸引,先變為橢圓形,然后在附加壓力影響下潰滅。
2)由于兩個空化泡之間產生的低壓區和附加壓力產生的壓差較小,所以在研究附加壓力和距離的范圍內并未產生二次潰滅現象。
3)隨著附加壓力的增大,空化泡的潰滅時間縮短,基本呈現線性關系。
4)在特定的附加壓力下,兩個空化泡在遠壁區潰滅時間隨距離的增大而減小,呈現線性關系,且當λ>0.6后,空化泡之間的相互作用對潰滅的影響基本可以忽略。

