二沉池數值模擬中湍流模型的發展與應用

(廣州大學 廣東 廣州 510006)

引言

重力沉降是給水處理廠和污水處理廠中最常用的一種去除水中懸浮固體(SS)的方法，一般來說整個沉淀池構筑物的造價占水廠總造價約30%。二沉池的主要作用是使活性污泥濃縮沉降，SS濃度要遠高于初沉池，因此，二沉池中的流態，污泥的密度將會影響到池體內活性污泥的沉降效果。Ekama和Marais1曾評述說，二沉池“是限制污水廠的處理效果的瓶頸”。

目前，絕大多數的二沉池設計都依靠于經驗參數，主要設計參數為表面負荷，而其他對于沉淀效果影響較大的參數則鮮有探究。2

而對一個新型沉淀池來說，在反應器加工以及對其進行試驗研究之前，了解和掌握反應器內的水流流態和流體結構是一個十分有意義的過程。CFD的出現為我們對流體的了解提供了極大的便利。

一、基本控制方程

任何封閉系統，都必須滿足三個基本方程——質量守恒定律、動量守恒定律和能量守恒定律；其中能量守恒定律針對有熱交換的流動系統；而質量守恒定律和動量守恒定律規定了物理量在單位時間、單位體積內的守恒規律，可以用一個統一方程對兩個定律進行描述：

(1-1)

其中，φ——通用變量(代表vx，vy，vz，Γφ等因變量)；

Γφ——廣義擴散系數；

Sφ——廣義源項；

ρ——流體密度；

(一)質量守恒方程

流體流動必須滿足單位時間流入的質量與流出的質量之差，等于控制系統內部流體質量的增量，也就是連續性方程，在連續方程中：φ=1，Sφ=0，Γφ=0，因此其微分形式為:

(1-2)

對于不可壓縮流體，流體密度ρ為常數，方程可簡化為

(1-3)

(二)動量守恒方程

(2-1)

(2-2)

(2-3)

(三)能量守恒方程

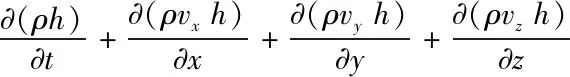
(3-1)

其中：λ——導熱系數；

Sk——熱源；

h——比焓；

Φ——耗散函數

二、沉淀池數值模擬的發展

從一維模型發展到三維模型，沉淀池的數值模擬理論得到了一系列的優化和改進。一維模型建立于肯奇的固體通量理論，固體通量理論基于一個假設：顆粒的重力沉降速度只取決于它所處位置的污泥濃度。水流被簡化為單純的上向和下向以簡化沉淀過程。然而一維模型中忽略了許多影響沉淀的變量，在很多實際情況下并不適用，因此有人提出將被忽略的物理變量重新加入模型中。

在沉淀池沉降的數值模擬中，最常用的湍流模型為k-ε模型及其變種：即標準k-ε模型、RNGk-ε模型和可實現的k-ε模型。

(一)標準k-ε模型

Larsen3對矩形沉淀池進行了探討，并在矩形沉淀池的基礎上建立起對應的二維數學模型。他運用流體力學方法分析池內的水力運動規律和懸浮物分布情況，并在過程中首次引入渦旋和流函數的概念，被后來者稱為CFD的先驅，為后來的CFD研究構建了框架。為了降低數學模型的復雜程度，Imam4和等人都對模型的改進進行了研究改進。Imam等人提出用有限差分法對沉淀池模型進行數值求解，完善了Larsen的實驗，模擬結果和實驗結果具有較高的一致性。實驗進行了一個關鍵性假設：湍粘度恒定不變。然而，湍粘度實際上取決于二沉池中的湍流狀態，不同池體、池體的不同部分也具有不同的湍粘度，因此湍粘度恒定假設大大的限制了該模型的準確性。為解決這一缺陷，Launder和Spalding5提出了更先進的模型：標準k-ε模型。此模型解決了湍流方程中的兩個重要變量k(湍動能)和ε(湍動能耗散率)，然后用k和ε的值計算湍流粘度，ε方程是個精確方程，ε方程是由經驗公式推導出來的方程，因此該模型算是一個半經驗公式:

(4-1)

k方程：

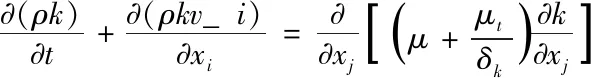
(4-2)

ε方程：

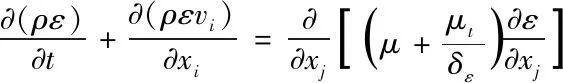
(4-3)

其中：ρ——流體密度，kg/m3；

vi——各方向時均速度的分量；

Gk——由層流速度梯度產生的湍動能；

Gb——由浮力產生的湍動能；

YM——在可壓縮流中，過度的擴散產生的波動；

δk、δε——兩個方程的普朗特數；

Sk、Sε——用戶自定義常數；

(二)RNGk-ε模型

標準k-ε模型被應用與許多研究之中，但該模型假定湍流為各向同性的均勻湍流，在非均勻湍流問題的計算中存在誤差，因此誕生了兩個由標準k-ε模型改進而來的湍流模型——RNGk-ε模型和可實現的k-ε模型。

RNGk-ε模型類似于標準k-ε模型，它來源于嚴格的技術統計，在計算模擬的準確性上卻優于標準k-ε模型。該模型最早由Yakhot和Orzag6提出，該模型在ε方程中增加了一個附加項，使得在計算速度梯度較大的流場時精度更高；模型中考慮了旋轉效應，對旋流計算精度也更好；模型中包含計算湍流普朗特數的解析公式，而標準k-ε模型用的是常數；標準k-ε模型是一個高雷諾數模型，而RNGk-ε模型對近壁區進行適當處理后可以計算低雷諾數效應。總的來說，RNGk-ε模型對于強旋流或帶有近壁流動的流場模擬有更高的優越性。

湍動能k方程：

(5-1)

湍動能耗散率ε方程：

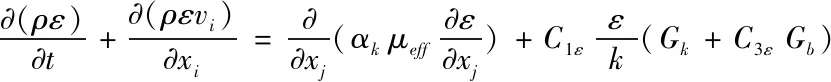
(5-2)

(5-3)

其中：ρ——流體密度，kg/m3；

vi——各方向時均速度的分量，m/s；

Gk——由層流速度梯度產生的湍動能；

Gb——由浮力產生的湍動能；

YM——在可壓縮流中，過度的擴散產生的波動；

αk、αε——兩個方程的普朗特數；

Sk、Sε——用戶自定義常數；

C1ε、C2ε、C3ε——常數，分別為1.44，1.92，0.09

(三)可實現的k-ε模型

可實現的k-ε模型對于標準k-ε模型的改進在于，該模型采用了新的湍粘度公式，此外，ε方程是同渦量擾動均方跟的精確運輸方程推導出來的。該模型滿足對雷諾應力的約束條件，因此在雷諾應力上保持與真實湍流一致，在模擬射流、邊界流等數值模擬中取得了較好的效果。

(四)其他模型的研究與發展

Raimund Bürger7等人提出了一種用于污水處理系統中所有過程建模的一致性建模方法。一致性建模方法的一個關鍵原則是，對于發生在連續時間和空間中的真實過程，建模應該在連續時間和空間中進行，從而產生一個偏微分方程作為數學模型。在偏微分方程的支持下，在離散時間和空間點(或層)上定義仿真模型。

三、沉淀池數值模擬的應用

(一)標準k-ε模型

標準k-ε模型是較早出現的、最廣為人知的用于描述湍流運動的模型，該模型的穩定性、經濟性和精確性在早期的數值模擬中是相當優秀的。

李雨陽8等用標準k-ε模型對多層平板單元組合沉淀池建立了三維數學模型，對沉淀池的固液分離進行了模擬，利用該模型探究出最佳的平板數、最佳污泥濃度和最佳池長，利用該數學模型為沉淀池的優化確定了改造方向，具有一定的指導意義。

蘇俊偉9等同于采用標準k-ε模型進行數值模擬，該實驗對二沉池進行了固液兩相流模擬，探究在不同入口流量下二沉池內固液兩相動力學行為的改變。從模擬結果發現，

涂有笑10利用標準k-ε模型和混合模型模擬對不同配水區高度下斜管沉淀池的流場、懸浮物濃度場進行了數值模擬。結果表明，配水區高度的增加可以降低配水區平均湍動能，增加配水均勻性，從而降低出水懸浮物濃度。

由于異向流斜管沉淀池在現有文獻上沒有可攻擊算水頭損失的公式和系數，在設計時取值困難，崔曉峰11等采用標準k-ε模型對水流流態、斷面流速分布與壓強分布等水力特性進行了研究，模擬得出的沉淀池水頭損失與實際工程測量結果吻合度不錯，找到了一種較為可靠的沉淀池水頭損失的計算方法。

(二)RNGk-ε模型

由于RNGk-ε模型相較于標準k-ε模在ε方程上多了一個附加項，使得在計算速度梯度較大的流場時精度更高，因此有不少研究者認為，RNGk-ε模型在某些沉淀池數值模擬上具有更大的優勢。

何志江12等人采用RNGk-ε模型對平流式二沉池進行模擬，分析污泥顆粒粒徑、表面負荷、擋板比例對出水懸浮物濃度的影響。模擬結果表明，最佳顆粒粒徑為300μm，二沉池中最佳擋板比例為60%，而表面負荷的增加會使出水懸浮物濃度和異重流比例急劇增加。這也證明了二沉池以表面負荷為主要設計參數的原因。

(三)可實現的k-ε模型

可實現的k-ε模型采用了新的湍粘度公式，且ε方程由渦量擾動均方根的精確輸運方程推導而來。理論上它可以更精確地模擬平面和圓形射流的擴散速度，并且在旋流計算、帶方向壓強梯度的邊界層計算和分離流計算問題中具有更高的擬合度。然而在Das等人的湍流模擬中，該模型并沒有顯現出更好的可靠性和優越性。該模型只考慮了流動的平均旋度作用，對湍粘度定義并沒有擴大，因此該模型需多重參考系，防止模擬中參數錯誤而對結果造成影響。

三、結論與展望

眾多研究表明，沉淀池數值模擬可以較為有效的預測池體內液體的流態。根據調整模型中的進水流速、污泥回流比、進水擋板、表面負荷、顆粒粒徑等因變量，可以對沉淀池的改進給出指導方向。

目前，國內沉淀池數值模擬最常用的模型為k-ε模型和RNGk-ε模型，這些模型在各自的研究中都具有不錯的擬合度，然而，數值模擬中仍然有不少可以改進的地方。

總體來說，沉淀池的數值模擬還是展現出了不錯的可靠性，且由于計算機硬件的高速發展，計算機硬件已經逐漸無法成為數值模擬的阻礙。相信在不久的未來，必定會出現更加貼合沉淀池湍流的模型出現，沉淀池數值模擬的應用也將得到更好的發展。