“分數的初步認識”中的“初步”與“認識”

陳士文　陸克榮

摘要：“分數的初步認識”第一課時的教學，可讓學生通過分一分認識到分數來自平均分，是一種發明與創造;通過折一折、涂一涂認識到分數是一個（數）量，是有大小的;通過寫一寫認識到分數和整數是相關聯的。

關鍵詞：分數的初步認識 認識幾分之一 平均分 數量 整數

數學學習中，從整數（實際是自然數）到分數，是學生經歷的第一次“數系的擴充”。從整數到分數的跨越，本質上是從離散量到連續量的跨越、從（一一對應）數數到（分割后用單位）測量的跨越。學生剛開始學習分數，無論對分數的意義和表示，還是比較和計算，都會感到困難。對此，蘇教版小學數學教材以螺旋上升的方式，分別在三年級上冊、三年級下冊、五年級下冊、六年級上冊，編排了《分數的初步認識（一）》《分數的初步認識（二）》《分數的意義和性質》《分數的加法和減法》《分數乘法》《分數除法》等單元，引導學生逐步學習，降低學習難度。

但是，在實際教學中，教師經常感到三年級“分數的初步認識”，尤其是第一課時《認識幾分之一》的教學不太好把握。下面，圍繞“初步”和“認識”這兩個關鍵詞，談一談《認識幾分之一》的教學該如何定位和實施。

一、關于“初步”——教學定位

教師可以從分數的產生、分數的形態、分數與整數的關聯三個方面思考“初步”體現在哪里。

（一）分數與平均分

“分數的初步認識”，應該讓學生感受到分數是因生活的需要而產生的：在分一分的過程中，因為整數不好表達小于1的物體（不足1的部分），所以，分數產生了。不必上升到分數是因生產的需要或數學自身的發展而出現的——當然，平均分的過程無形中蘊含了分數與除法的關系。此外，對于“分數是建立在平均分基礎上的”這一本質，還應該讓學生充分認識各種平均分，尤其是一些看上去不是但實際上是的平均分（所分的各部分不能完全重合，但從度量的角度看是一樣大或多的）。

（二）分數的量與率

整數是直接從具體事物中抽象出來的。分數是先“分”而后得的“數”，比整數更抽象。整數的認識是從一個個具體的量開始的。比如，從一朵花、一個蘋果、一支筆、一本書等，逐步形成數字“1”的概念。因此，分數的認識如果也從“量”開始，則學生容易接受。即：在分數后面綴上單位，如1/2個、1/3塊、1/5杯等，學生容易理解。因此，“分數的初步認識”，不必涉及“率”。

（三）分數與整數

分數認識是整數認識的擴展，分數和整數始終在一起。比如，分數3/4可看作平均分整數1為4份，取其中的3份;也可看作平均分整數3為4份，取其中的1份。即：3/4=1/4×3或3/4=3÷4。3/4的背后是整數1或3。因此，“分數的初步認識”，要以整數為基礎，聯通到整數單位，不能孤立地認識，也不必過多地應用（解決實際問題）。

二、關于“認識”——教學實施

知道了“初步”認識的內容及其程度后，就要思考如何“認識”。我們通過教學片段來說明。

（一）分一分，發現分數來自平均分

師同學們，今天這節課我們認識新的數。新的數在哪里呢？（出示圖片）這是一塊餅，小紅想一個人吃，那她可以吃幾塊餅？

生1塊。

師這時，小亮來了。好東西要和朋友分享，怎么分享呢？

生從中間分開，一人吃一半。

師為什么要從中間分開呢？

生兩份一樣大，分得公平。

師這種分法叫作怎么分？

生平均分。

師這樣每人吃幾塊？

生半塊。

生二分之一塊。

師半塊就是二分之一塊。一塊餅平均分成兩份，其中的一份就是二分之一塊。這個數你以前學過嗎？

生沒有。

師這就是今天我們要認識的新的數，叫作分數。誰聽明白二分之一塊的意思了？請說一說。

（學生說。）

師如果是一大一小這樣分的，還能說分了二分之一塊嗎？

生不能。

師分的方式是平均分。（介紹分數各部分的名稱：分子、分母、分數線……然后出示圖片）巧克力、飲料、紅紙條為什么都用分數，而不用以前認識的1、2這樣的整數來表示？

生巧克力沒有1塊大，飲料不滿1杯，紅紙條沒有1米長，我們用分數1/3、1/5、1/6來表示。

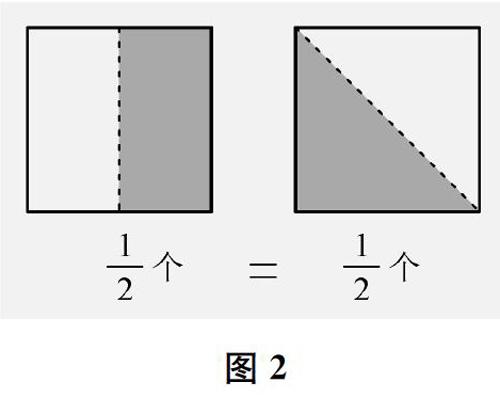
師（出示圖1）圖中陰影部分為什么能用分數表示？它好像不是平均分。

生（思考片刻）它是平均分。把大正方形橫豎對折，分成四個小正方形，每個小正方形中，陰影部分和空白部分都一樣大，是平均分。

師非常好！大家要特別注意那些看上去不像平均分的平均分哦。以往學的是整數，今天整數不好表達了，就產生了新的數。分數是在“分”的過程中出現的。

借助餅、巧克力、飲料、紙條等不同素材，引導學生在分一分中感悟：分數是在生活表達遇到困難時人們的一種發明與創造。此處，既要讓學生知道知識（分數各部分的名稱），又要讓學生增長見識與智慧（分數的發明與創造）。

（二）折一折、涂一涂，發現分數有大小

師剛才我們分一分，找到了今天要認識的新的數。現在請同學們拿出一張正方形紙，折一折、涂一涂，表示出分數。

（學生活動。）

師（出示下頁圖2）誰愿意說一說你是怎么做的？

生把紙對折，涂上一份。

師對折和我們黑板上的哪個詞意思一樣？

生平均分。

師有同學表示出了1/4。說說看。

生把紙對折，再對折，涂上一份。

師如果老師用同樣的方法去涂1/2和1/4，哪個涂得快？

生1/4涂得快，因為1/4小。

師還有誰表示的分數讓我們涂得更快？

生1/8。

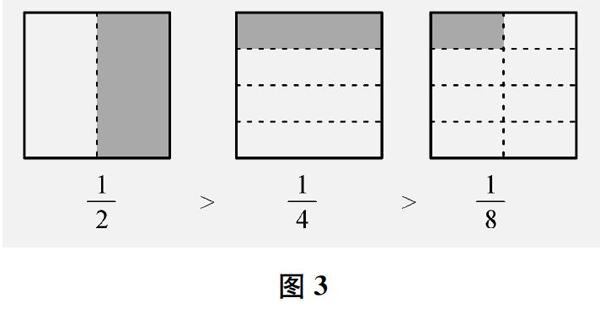
師（出示圖3）我把這些分數展示在屏幕上，你有什么發現？

生我們涂的時候，感覺分數是有大小的。

師你能想一想為什么分數有大小嗎？

生平均分的份數不同。分得越多，每一份越小，分數也就越小。

師以前我們認識的整數有大小嗎？8和4相比哪個大？1/8和1/4呢？

生8大，1/4大。

師分數和整數都有大小，不過比較的方法有些不同，你們能體會到嗎？

直觀地看可以發現分數的大小，動手去涂可以感受分數的大小。但僅僅這樣“認識”是不夠的，還應該從平均分的份數多少上說明分數的大小，以及自然地聯系到整數的大小比較，發現其與分數大小比較的不同之處。

（三）寫一寫，發現分數和整數相關聯

師我們分過了，也涂過了，下面來寫一寫吧。（出示圖4）這是一塊黑板，用1來表示。（同步指圖）其中這一塊是“科學天地”，這一塊是“藝術園地”，剩下的是“智慧園地”。你在上面看到了哪些分數，在作業紙上寫一寫。

生（展示）1/2、1/4、1/4。

師一塊黑板是整數1，同學們在圖中找到了三個分數，真厲害！（出示圖5）這幅圖，你能寫出哪些整數？

生1、3，1、9。

師你還能找到分數嗎？

生1/3、1/9。

師我們今天學的是新的數——分數。在圖上，我們看到了分數的分子、分母所表示的整數，說明分數和整數是有關聯的。

通常的看圖寫分數只是一般技能。而此處的看圖寫分數具有整體的視野：既寫分數，又寫整數，在寫的過程中，感悟分數與整數的聯系。

參考文獻：

[1] 遠山啟.數學與生活（修訂版）[M].呂硯山，李誦雪，馬杰，等譯.北京：人民郵電出版社，2014.