基于位移信號的磁懸浮飛輪轉速估計

劉 虎，楊振鵬*，武登云

(1.北京航空航天大學 儀器科學與光電工程學院，北京100191； 2.北京航空航天大學 新型慣性儀表與導航系統技術國防重點學科實驗室，北京100191； 3. 北京控制工程研究所，北京 100080)

1 引 言

磁懸浮飛輪是目前較理想的姿態控制執行機構[1-2]，所使用的磁懸浮軸承的免接觸特性使其具有長使用壽命、在無須潤滑的特點[3-5]，而且，磁懸浮飛輪通過數字控制器可以實現主動振動控制，從而對不平衡擾動進行抑制，保證姿態控制精度。

對于磁懸浮飛輪的不平衡振動的抑制問題，國內外學者做了很多研究，可以采取自適應LMS(Least Mean Square)算法[6]、重復控制[7]、卡爾曼濾波[8]等方法來實現。其中陷波器[9-10]是使用較為普遍的方案，而通過陷波器對不平衡的振動過程中轉子的精確轉速信息不可缺少。

在磁懸浮飛輪系統中，轉速的獲取通常通過霍爾轉速傳感器來實現，磁懸浮飛輪通過計算單位時間內傳感器上接收到的轉子脈沖數量處理后得到轉速，可以得到精確的轉速信號。由于安裝偏差和磁場干擾等因素的存在，傳感器測速結果難免有誤差，且傳感器故障時，失去轉速信號將導致系統無法進行振動抑制。此外，對于磁懸浮球等應用，無法安裝霍爾傳感器或者編碼器進行測速。因此，需要考慮無測速傳感器情況下的振動抑制方法。文獻[11-12]中提出使用自適應觀測器、鎖相環等方法估計不平衡振動信號的幅值頻率，但未考慮倍頻信號而無法保證振動控制效果。由于傳感器檢測面、轉子不平衡質量等因素的存在，磁懸浮飛輪轉子位移傳感器傳感器信號中存在豐富同頻和倍頻分量，為轉速檢測提供了新的途徑。Chen[13]通過自適應陷波提出磁懸浮轉子徑向x,y兩軸同頻位移信號，并假設兩者同幅度且正交，但由于安裝誤差及系統參數的不對稱，多數系統并不滿足位移信號正交和幅度一致的條件。張染[14]基于位移傳感器信號的中高倍頻分量提出采用Hilbert變換進行經驗模態分解和譜分析求取轉速，具有較高精度，但由于低頻時的倍頻成分易受污染導致該方案不能在全轉速情況下適用。

本文提出一種通過飛輪某個方向位移量預測轉子轉速的估計方法，利用神經網絡對非線性模型的擬合優勢，在輸入輸出關系式無法確定的情況下能按照輸出誤差值調整內部參數使得估計模型符合實際的輸入輸出。該方法依據已知的位移和轉速數據，構建神經網絡模型，并通過網絡參數調整達到較好訓練效果，具有良好的測速精度，實驗誤差在20轉左右，相對于張染[14]所提出的方法，拓展了轉速辨識的范圍；在MATLAB/Simulink中構建了磁懸浮飛輪的模擬系統，并加入神經網絡模塊進行仿真，并在磁懸浮飛輪樣機上進行了轉速估計試驗，仿真及實驗結果體現該方案的可實現性及精度。

2 基于位移信號的轉速估計原理

在磁懸浮飛輪系統中，轉子運行時會因各種干擾作用而偏離平衡位置，需要不斷調整控制電流從而改變電磁力大小使轉子回到期望位置，而這個過程調整的依據便是轉子的位移，因而與轉速傳感器不同，系統中必須載有位移傳感器，渦流位移傳感器的輸出可以表示為：

(1)

式中：x表示傳感器所測方向位移量，A表示位移幅值，n表示諧波次數，ω0表示轉子轉頻，φ表示初始相位。可知位移信號中的同頻信號和倍頻信號都包含了轉子轉速信息。

將式(1)寫作如下形式：

(2)

再將式(2)進行傅里葉變換，得到：

(3)

式中δ表示沖激函數。

考慮其中頻率值大于0的成分，得到：

(4)

初始相位φ在[0,2π]區間內變化，相比于分母nω0很小，初始相位的變化帶來的影響可以忽略不計，可知位移量頻域成分是關于轉速ω0的函數，但具體函數關系式由于缺乏相關理論研究難以得知。

而神經網絡模型具有良好的非線性擬合能力，選定網絡的層數、神經元數及激活函數F后，通過初始化網絡權值W，再將位移量X作為輸入導入網絡模型，線性疊加后通過激活函數處理得到預測輸出O，即：

O=F(WX).

(5)

將網絡預測輸出O與期望輸出(轉頻值)R比較得到誤差值E，通過求導等方式用以更新網絡權值W，重復該過程直至誤差E符合要求，從而得到一個以位移量X和轉子轉頻R為輸入輸出，通過網絡權值X和激活函數擬合函數特性的網絡模型用以估計轉速。

圖1所示為磁懸浮飛輪轉子某方向位移信號的瀑布圖。對于位移信號中的同頻分量，其誘發因素包含轉子的不平衡質量、傳感器檢測面不均勻以及磁場不均勻等，而倍頻信號是傳感器安裝偏差和磁軸承非線性等引起的，磁軸承非線性指的是磁軸承系統的電磁力與轉子位移和控制電流之間的非線性關系，這些都是難以避免的因素，因而倍頻信號是位移傳感器輸出中無法避免的成分，且倍頻信號包含轉子轉頻信息，因而倍頻信號可以充當轉頻信號獲取的一個有效途徑。

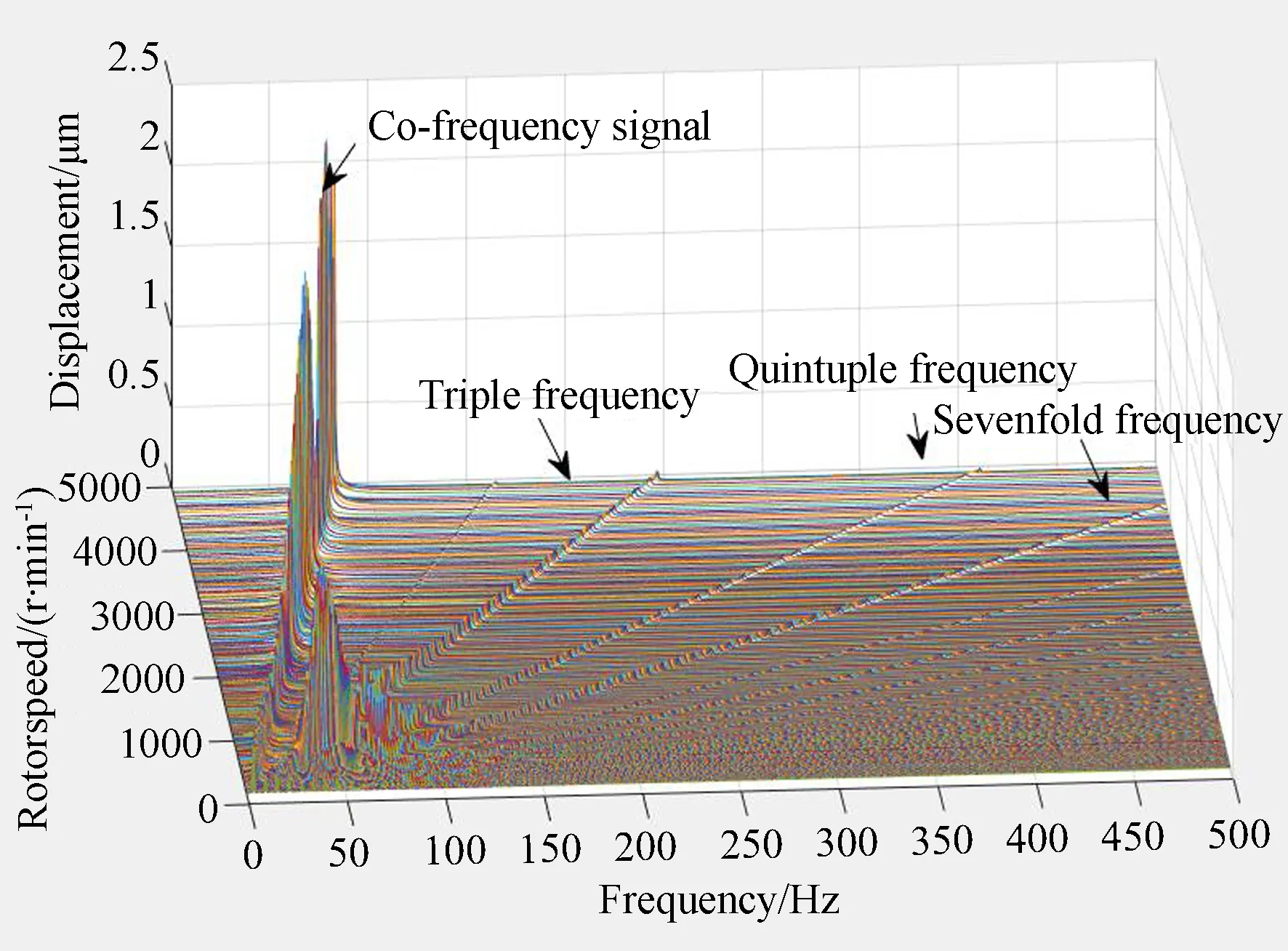
圖1 位移信號瀑布圖Fig.1 Rotor displacement signal waterfall

3 磁懸浮飛輪系統模型

如圖2所示為磁懸浮飛輪的結構圖[15]，包含一對軸向磁軸承和一個徑向磁軸承，其中軸向磁軸承用以控制轉子徑向扭轉和軸向平動，徑向磁軸承控制徑向平動。磁軸承通過電磁力控制轉子懸浮，轉子所受電磁力線性化[16]后公式如下：

(6)

式中：m表示轉子質量，x表示轉子位移，i表示控制電流，kx表示位移剛度系數，ki表示電流剛度系數。

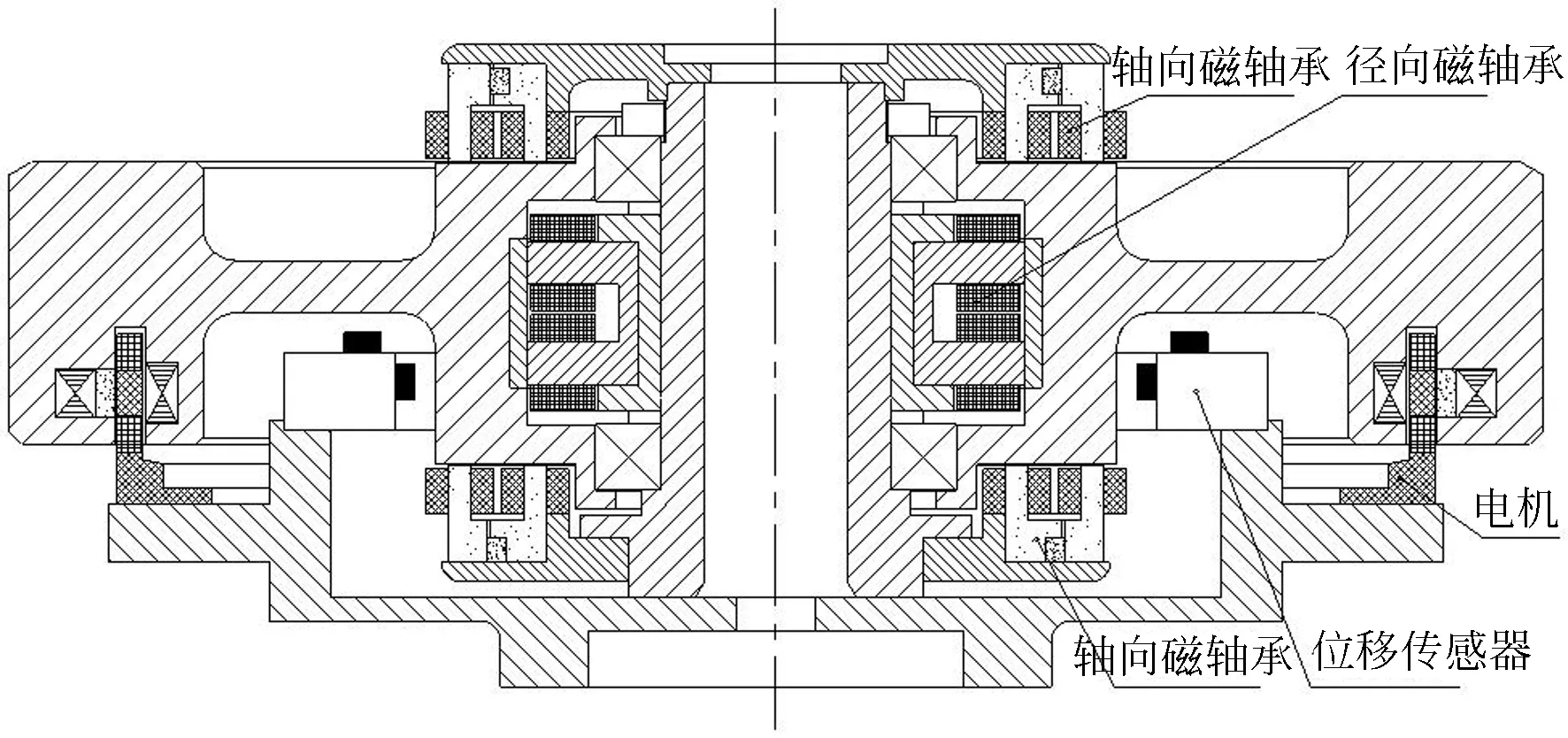
圖2 磁懸浮飛輪結構圖Fig.2 Configuration of magnetic suspended flywheel

如圖3所示為磁懸浮飛輪系統示意圖，飛輪工作時，通過轉子的位移量反饋控制信號和陷波器的振動抑制反饋信號疊加放大，用以調整飛輪中繞組線圈電流值，從而調整飛輪轉子所受電磁力，以保持飛輪穩定懸浮工作。

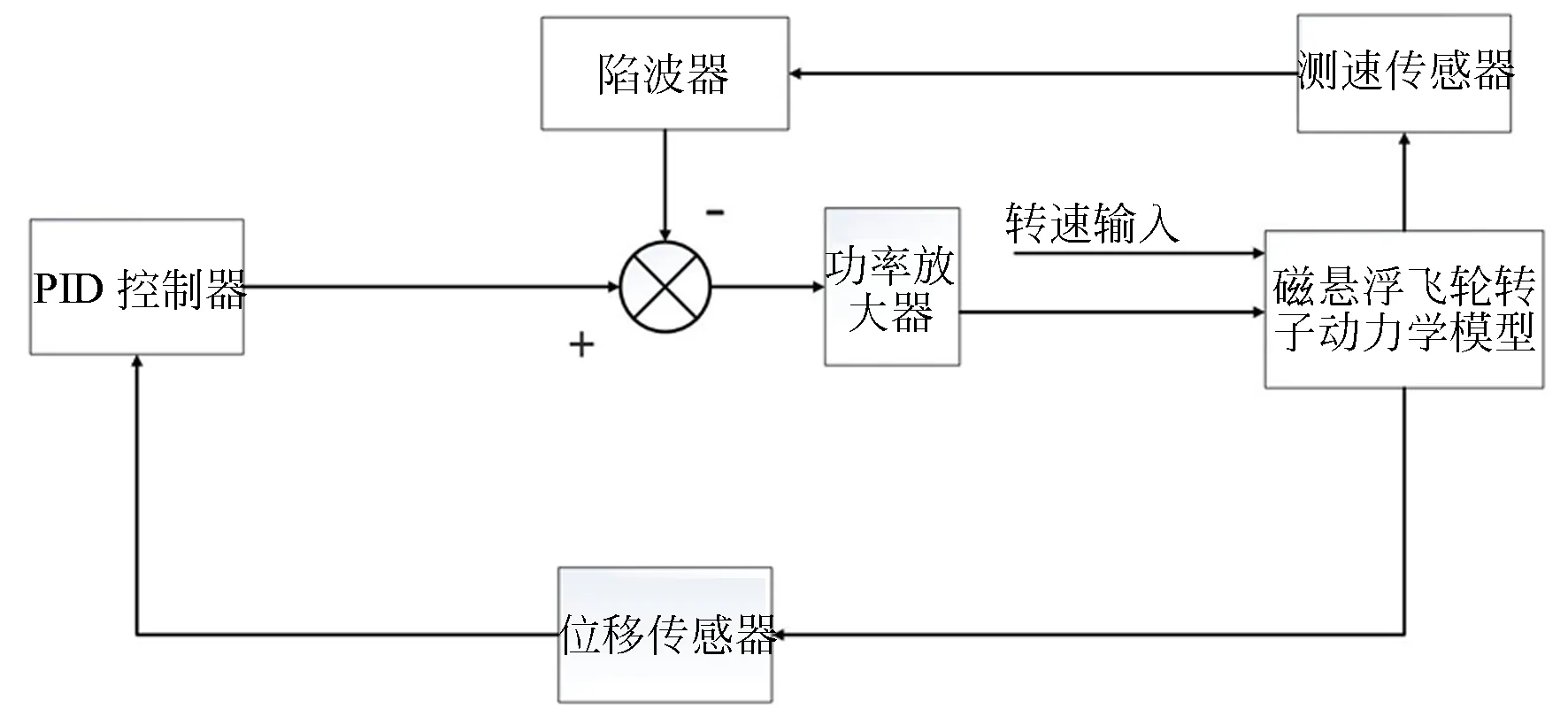
圖3 磁懸浮飛輪系統框圖Fig.3 Magnetic suspended flywheel system

圖4所示為飛輪轉子的動力學模型，其中r，i分別表示輸入轉速和線圈電流，m為轉子質量，kub為靜不平衡度(為簡化模型，仿真過程僅考慮轉子靜不平衡)，d為隨機噪聲。圖5所示為陷波器結構示意圖，其中ω為轉子轉頻。

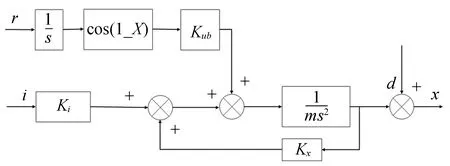
圖4 磁懸浮飛輪轉子動力學模型Fig.4 Dynamic model of magnetic suspended flywheel

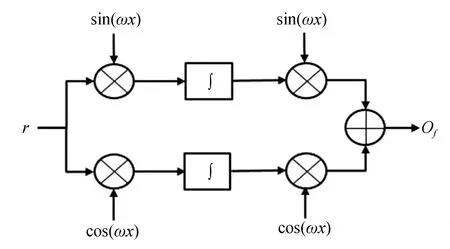
圖5 陷波器結構圖Fig.5 Configuration of notch filter

4 神經網絡訓練

由于測速傳感器的安裝誤差等局限性，本文提出通過訓練神經網絡模型進行轉速估計的方案來替代測速傳感器，以位移信號和轉速信號分別作為模型輸入輸出，構建經典BP(Back Propagation)神經網絡，通過LM(Levenberg-Marquardt)法訓練，將得到的模型用以實時轉速估計。

4.1 BP神經網絡

BP神經網絡[17]是目前應用最廣泛的神經網絡，是一種全連接式的前向傳播網絡,圖6是一個簡單的三層神經網絡，由輸入層、一個隱含層和輸出層組成。網絡包含函數信號和誤差信號，函數信號從輸入層正向傳播經過隱含層至網絡輸出層，而誤差信號從輸出層反向傳播經由隱含層到達輸入層，并在此過程中調整相鄰網絡層之間的權重和偏置。

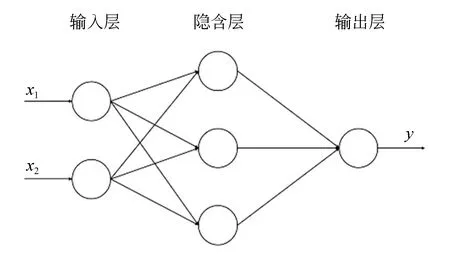
圖6 BP神經網絡示意圖Fig.6 BP neural network

圖6中每個單元對于一個神經元，模型如圖7所示，神經元將輸入進行線性組合后經由一個非線性映射的激活函數得到輸出值。神經網絡具有很強的非線性系統擬合能力，并且可以通過增加隱含層層數和突觸數目提升擬合效果。同時，當網絡的隱含層中節點(即突觸結構)太少，網絡的學習能力和對信息的處理能力均會大打折扣，然而數量過大時，一方面使網絡過分龐大復雜，學習過程陷入局部極小點的可能性增大，達不到最好的效果，另一方面還增加了學習過程的耗時。對隱含層節點數目的選取并沒有一個完整理論，但可以通過一個經驗公式[18]提供參考：

0.51,

(7)

式中m，n分別表示輸出層和輸入層神經元數。

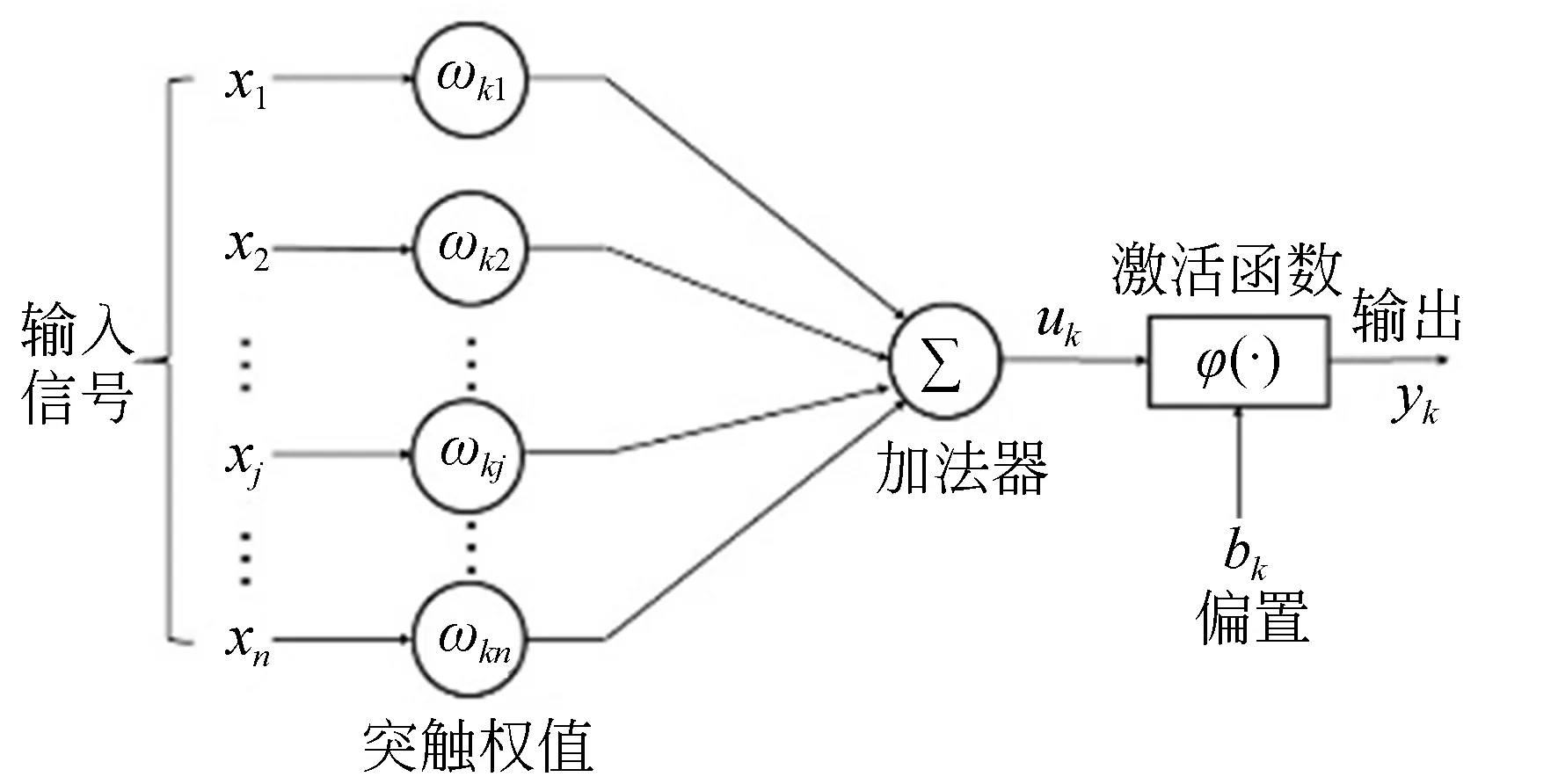
圖7 神經元模型Fig.7 Artificial neuron model

4.2 LM算法(Levenberg-Marquardt)

列文伯格-馬夸爾特法(Levenberg-Marquardt，LM算法)通常是收斂速度最快的訓練算法，是有監督學習使用較多的算法，局限之處在于運算過程中相比其他算法需要占用較大存儲空間。LM算法是將梯度下降法和高斯-牛頓法結合而成的[19]，兼具二者的優點，該算法下權重值更新的表達式為：

Δw=-[JT(w)J(w)+μI]-1JT(w)e(w),

(8)

其中：μ為LM法自適應參數，I為單位矩陣，e(w)表示神經網絡的代價函數，J(w)代表雅各比矩陣，表達式如式(9)所示：

(9)

當μ取值為0時算法變成了高斯-牛頓法，當μ趨近無窮時則實現梯度下降法的功能。

5 仿真及實驗

5.1 仿真系統參數

磁懸浮飛輪轉子系統的結構與仿真參數如表1、表2所示。

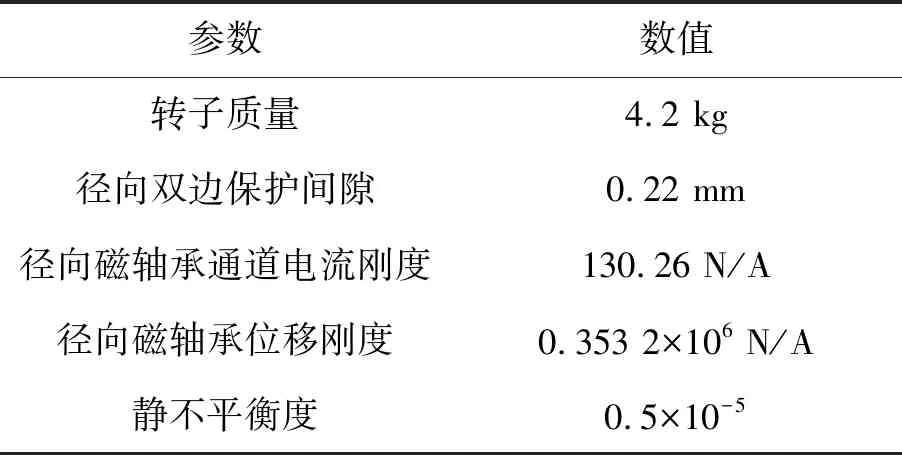
表1 磁懸浮飛輪結構參數Tab.1 Structural parameters of magnetic flywheel

表2 磁懸浮飛輪仿真參數

Tab.2 Simulation parameters of magnetic flywheel

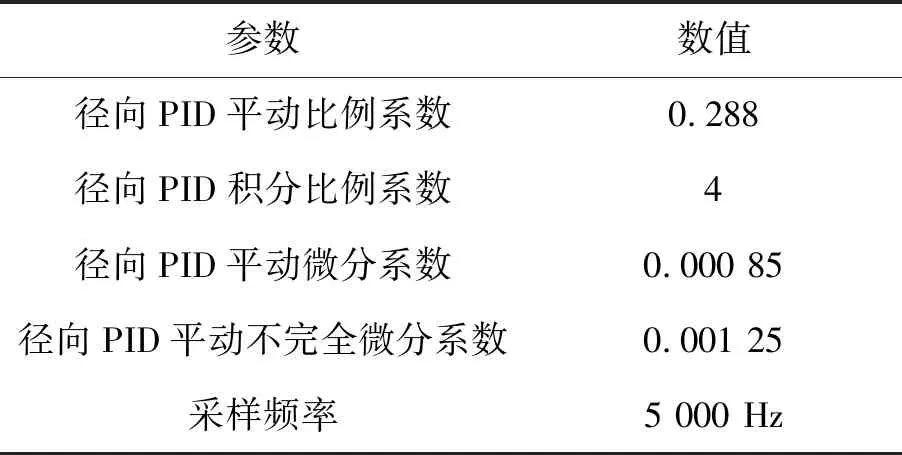
參數數值徑向PID平動比例系數0.288徑向PID積分比例系數4徑向PID平動微分系數0.000 85徑向PID平動不完全微分系數0.001 25采樣頻率5 000 Hz

5.2 數據的獲取及處理

在仿真系統的基礎上，采集一組飛輪升速過程的轉速和位移數據，求取位移量的頻譜。由位移的瀑布圖可知，倍頻量中的1，3，5，7倍頻為主要成分，依據位移量各倍頻點幅值的極值特性采集3，5，7倍頻的位移分量及其頻率值和飛輪轉速值，隨機選取其中95%用作模型構建，其余用以測試模型的準確度。

神經網絡模型構建前，為防止因輸入輸出的數量級差距太大導致網絡估計誤差增大，同時加快網絡訓練收斂速度，需先將數據經過線性歸一化處理至[0,1]區間，歸一化表達式如下：

(10)

式中：x，y分別表示歸一化前后的數據；xmin，xmax分別表示歸一化前的數據最值；ymin，ymax分別表示數據歸一化后的最值。

以歸一化后的位移量和轉速值分別作為輸入輸出構建一個5層，節點數分別為6，30，50，35，1的BP神經網絡，輸入層選取傳輸函數為tansig函數，各隱含層和輸出層傳遞函數為logsig函數。按照LM法進行訓練，得到一個用以轉速估計的模塊。

5.3 仿真結果

基于磁懸浮飛輪轉子系統及神經網絡轉速估計模塊，進行飛輪轉子恒速和變速兩種情況的仿真。

對于轉子恒速轉動情況的仿真，選取了轉頻分別為30 Hz(1 800 r/min)和85 Hz(5 100 r/min)的低、高速的仿真結果圖8，圖9所示。對于變速情況，模擬了飛輪以15 r/s的速度升速的過程，選取從3 000 r/min升速至5 000 r/min的轉速估計結果如圖10。

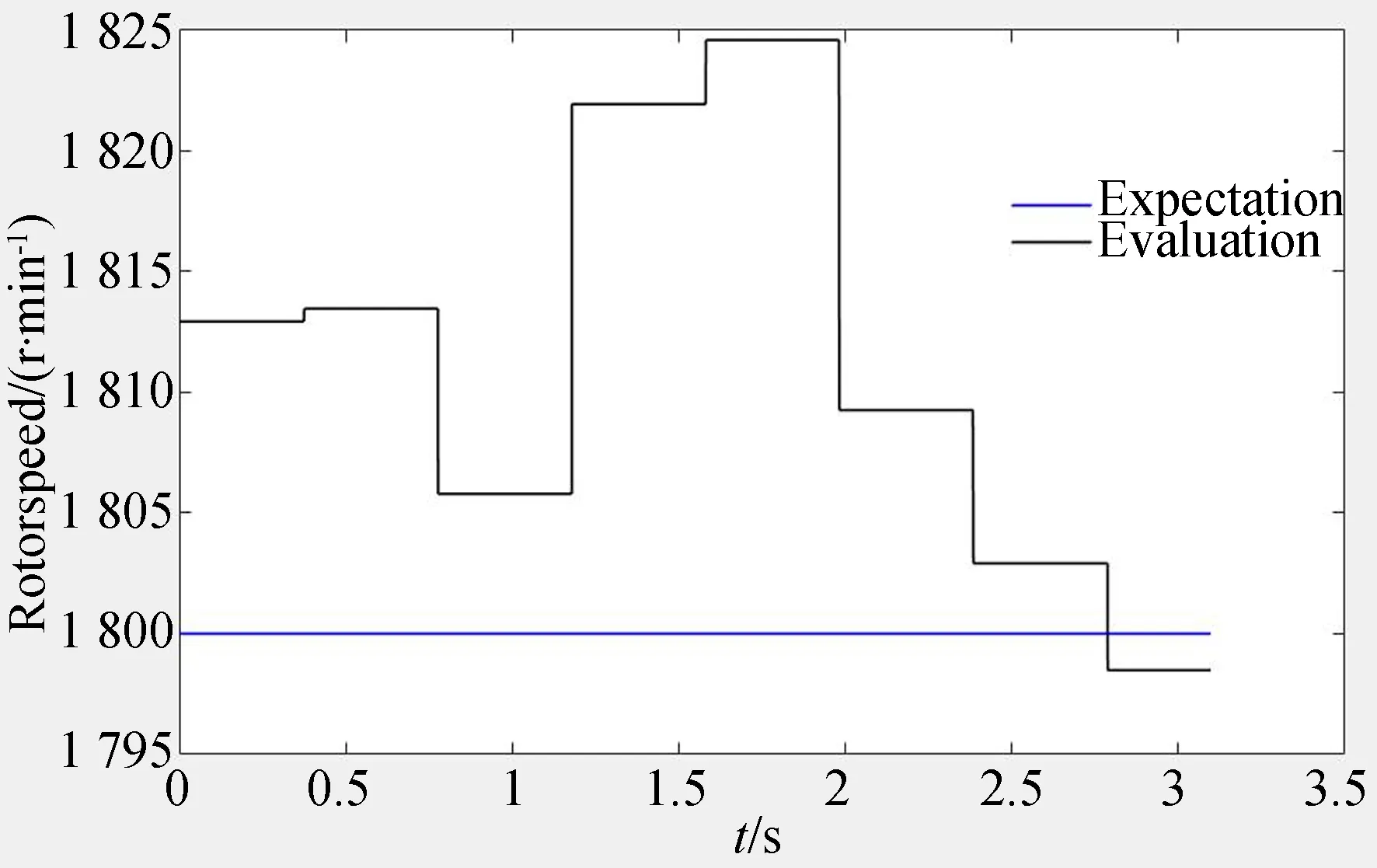
圖8 30 Hz轉速估計結果Fig.8 Rotorspeed estimation of 30 Hz

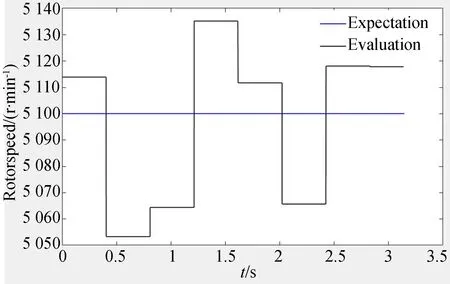
圖9 85 Hz轉速估計結果Fig.9 Rotorspeed estimation of 85 Hz

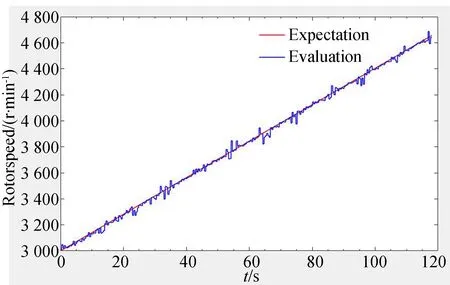
圖10 升速過程轉速估計曲線Fig.10 Rotorspeed estimation of acceleration process

每次轉速估計時，需要先采集2 048個點做傅里葉變換，從頻譜中采集倍頻極值點，所以具有一定延時性。由圖可見，磁懸浮飛輪轉子恒速運動時，估計誤差均未超過30 r/min，誤差百分比控制在2%以內。

在磁懸浮飛輪升速仿真過程中，轉速的估計曲線具有一些估計誤差較大的點，但絕對誤差控制在80 r/min以內，轉速估計精度稍差于飛輪恒速時，誤差百分比大約在2%。

5.4 實驗驗證

為進一步試驗本文所提的轉速估計方案的可行性，在某型號的磁懸浮飛輪系統上進行了實驗，系統如圖11所示。

圖11 磁懸浮飛輪及控制系統Fig.11 Magnetic suspended flywheel with controlling system

圖12 TMS320C6678評估板Fig.12 Evaluation board of TMS320C6678

磁懸浮飛輪系統除了飛輪、控制盒、電源及上位機，還借助采用主輔拓撲結構[20]的型號為TMS320C6678(如圖12所示)的DSP板塊及FPGA板塊，通過FPGA實現采樣等功能，經FPGA處理的數據通過DSP沿仿真器傳輸至PC機，通過PID控制算法再將控制信號傳回飛輪控制盒實現飛輪穩定懸浮。

將飛輪升速過程所記錄的位移數據和轉速數據導出至MATLAB處理，選擇其中一路位移信號求取頻譜圖像，并由此得到位移倍頻量，并歸一化處理。并以位移量和對應轉速分別作為輸入輸出，構建神經網絡模型，以LM法進行訓練，并通過模型參數調整達到最佳訓練效果，最終得到一個5層，節點數分別為6，16，20，16，1的神經網絡。同樣模型構建過程中，隨機選取90%的數據作為訓練。

剩余10%用以驗證模型的準確度。訓練數據誤差和驗證數據誤差曲線如圖13，圖14所示，可以得知本文所提方法的轉子轉速估計誤差在20 r/min以內，低轉速時誤差所占百分比相較于高轉速更大，但也控制在3%以內。

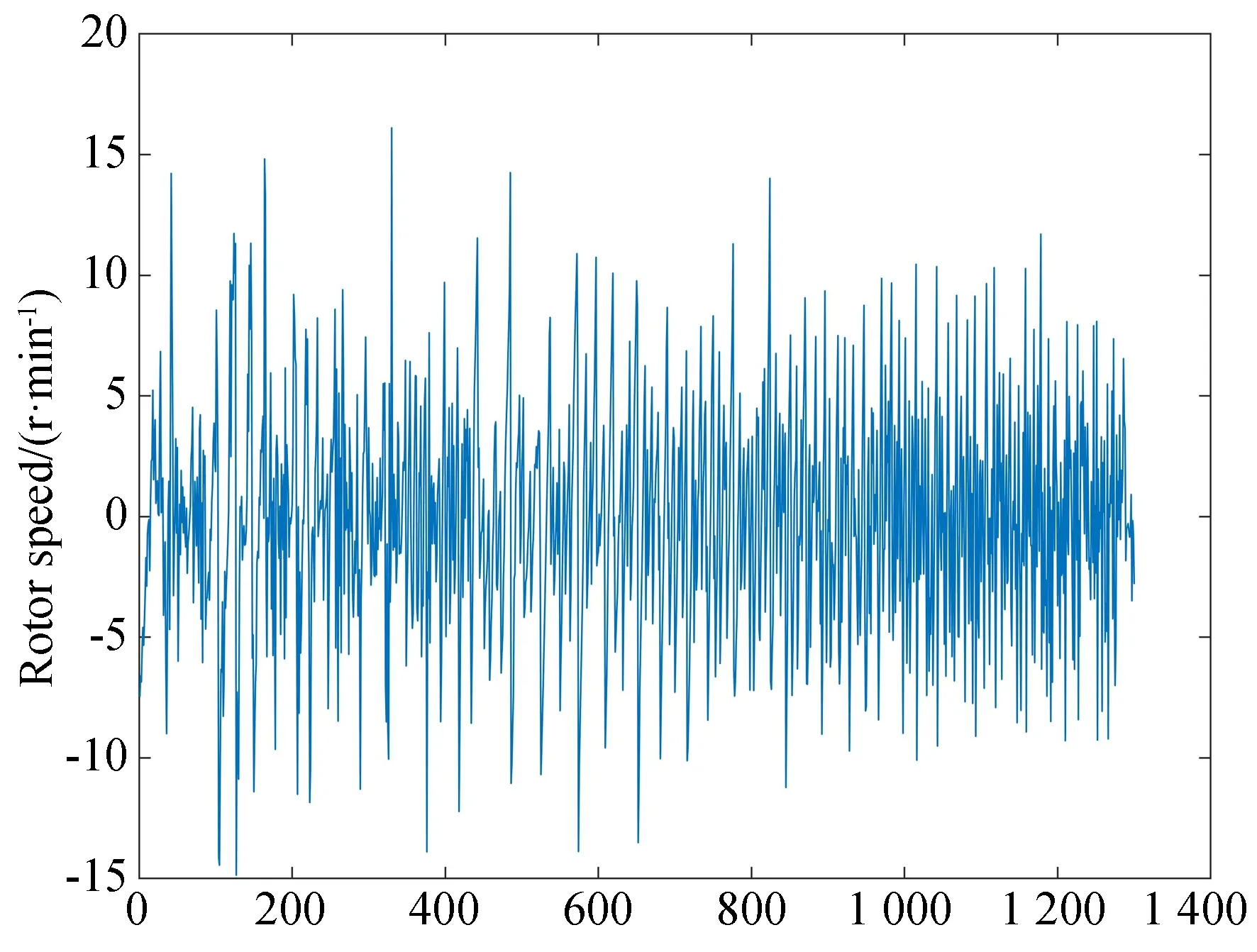
圖13 訓練數據絕對誤差值Fig.13 Absolute error of training datas

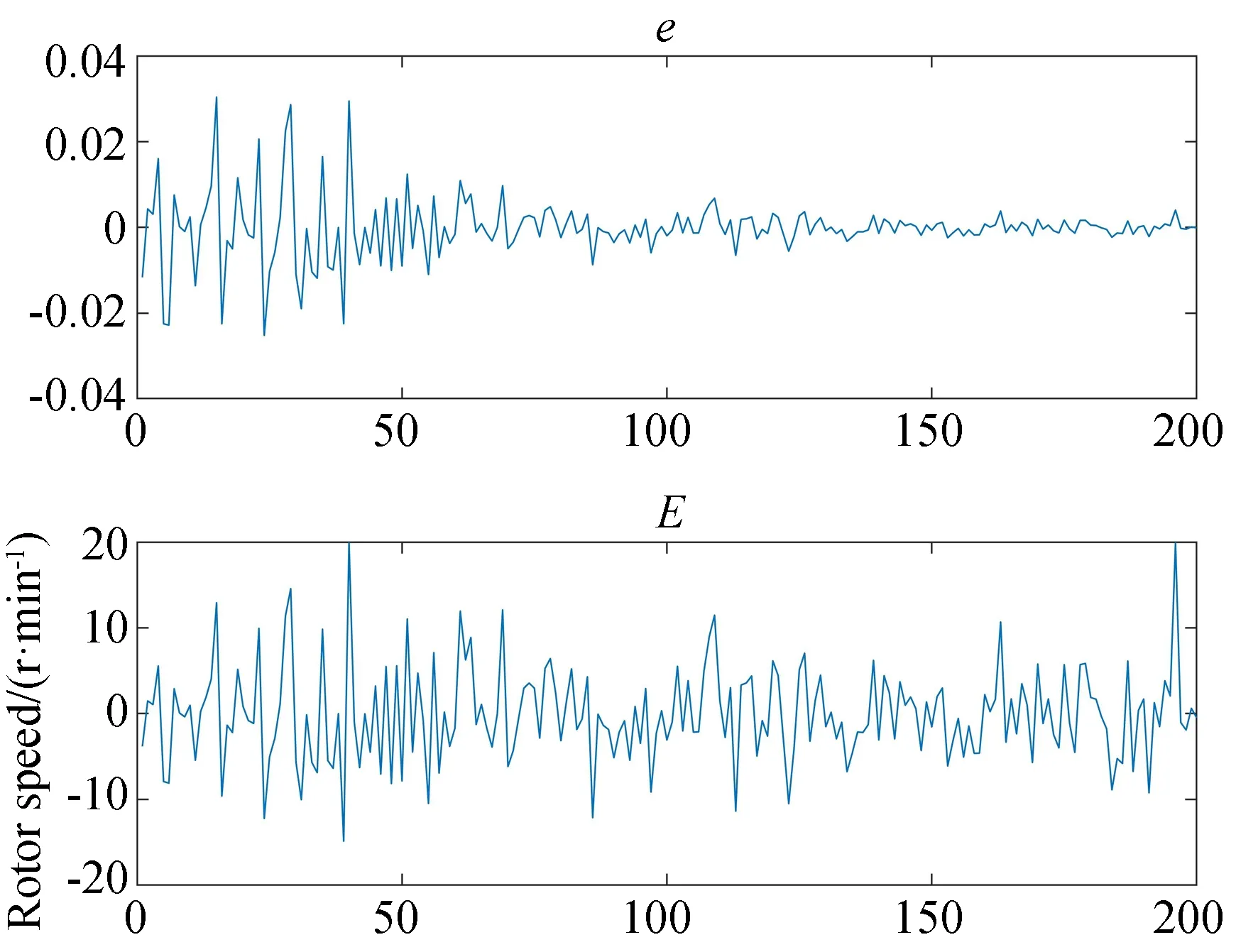
圖14 驗證數據相對誤差e和絕對誤差EFig.14 Absolute error and relative error of validation datas

6 結 論

本文針對無測速傳感器的磁懸浮飛輪系統的轉速獲取問題，提出了一種通過構建輸入輸出分別為飛輪某通道倍頻位移量和轉子轉速值的模型，實現得到高精度的實時轉速數據的方法，并在MATLAB/Simulink環境下對此進行了仿真實驗。仿真實驗分別在低速、高速情形下對轉子恒速和變速進行了轉速估計，轉速誤差最多至幾十(r/min)。然后在磁懸浮飛輪控制系統上試驗了該方法，轉速估計誤差小于20 r/min。綜上，結果表明了該方案用于磁懸浮球等無法配置測速傳感器的場景是具有一定可行性的。