平臺運動激勵下鋼懸鏈式立管觸地點動態分析

尤巖巖，白興蘭，王孟義

(1. 浙江海洋大學 船舶與機電工程學院，浙江 舟山 316022; 2. 浙江省近海海洋工程技術重點實驗室，浙江 舟山 316022)

隨著海洋油氣開發向深水發展，鋼懸鏈式立管作為連接浮式平臺與海底生產系統的關鍵裝備，在濕樹開發模式中具有良好的經濟性和適應性[1]。SCR頂端以一定的預張力連接浮式平臺而懸垂于海水中，另一端連接井口，與海床接觸后呈反彎形態，如圖1所示，立管常因觸地區的應力循環發生疲勞損傷。平臺運動是誘發立管動態行為和疲勞損傷的主要因素之一，因此研究平臺運動激勵下立管觸地區的動態行為和疲勞性能，對于準確預測管道的疲勞壽命與評估安全狀態至關重要。

由于不同的錨泊形式，平臺在風、浪、流作用下具有不同的運動特征，對立管的作用以運動耦合分析為主，如Elosta等[2]運用Orcaflex軟件建立SCR與半潛式平臺的分析模型，以平臺RAOs作為激勵條件，研究立管觸地區動力響應和疲勞性能相對于不同土參數和溝槽發展的敏感性。Wang等[3]運用DeepC得到平臺的動力響應，作為立管頂端響應輸入到ABAQUS的立管模型中，并考慮管土作用，開展了立管的整體動力分析。白興蘭等[4-5]考慮平臺的慣性力，基于CABLE3D建立了立管與平臺的整體分析模型，將二者連接處作為剛臂處理，而忽略了二者之間的相對運動。影響觸地區動態行為的另一重要因素是海床剛度模型，目前有三類模型用來模擬土對立管的作用，一是彈簧模型，二是RQ模型[6]，三是AB模型[7]。為了提高計算精度，后兩種非線性模型已經被寫入商業軟件，如Orcaflex、ABAQUS，并廣泛應用于立管觸地區的動態分析[8-9]，AB模型也被寫入CABLE3D程序中，用來分析管土相互作用[10-12]。Shiri等[9]利用非線性海床模型模擬管土相互作用，建立動態分析模型，研究觸地區溝槽深度對SCR疲勞壽命的影響。Wang等[13]通過優化分析提出了參數化溝槽模型，并研究了溝槽幾何尺寸對觸地區疲勞損傷的影響。Elliott等[14-15]運用離心機模型技術開發了管土相互作用的試驗系統，考慮流體-立管-海床土的交互作用，揭示溝槽形成及溝槽對觸地區疲勞損傷的影響。

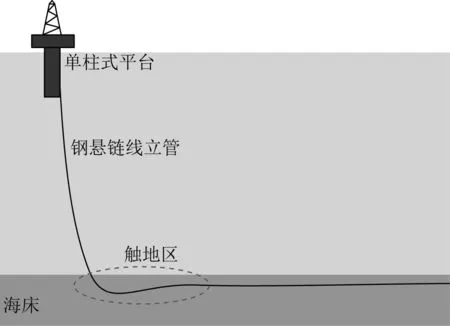
圖1 鋼懸鏈式立管結構示意[16]Fig. 1 Structural sketch of the SCR

上述研究主要圍繞平臺平面內的運動，特別是垂蕩運動對立管的影響，海床土模型僅考慮豎向作用。本文擬研究平臺三維運動激勵下立管觸地區的動態行為和疲勞分析，包括觸地點應力分布、貫入位移和疲勞壽命分布情況等，其中海床豎向作用采用RQ模型的土抗力-埋深曲線，側向作用采用庫倫摩擦“雙線”模型，縱向作用表現為接觸摩擦力，由土摩擦系數確定。

1 數學模型

1.1 控制方程

基于結構動力學原理，可得浮式平臺和立管的運動方程[5]：

(1)

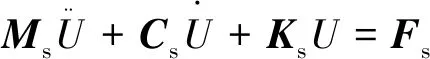
(2)

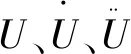
U=Tu

(3)

式中：u、U分別為懸掛點和平臺質心的六自由度位移列向量，T為轉換矩陣。將平臺質心的運動變換得到立管懸掛點處的運動，將式(3)代入式(1)并左乘變換矩陣的轉置可得：

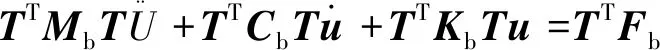
(4)

平臺運動將帶動SCR隨之運動，因此，結合式(2)與(4)可得平臺與立管的耦合運動方程：

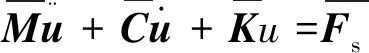
(5)

其中：

1.2 管土作用模型

圖2所示為豎向土體抗力與埋深的關系曲線，由Randolph和Quiggin根據模型試驗模擬得到[6]，簡稱為RQ模型，體現了加載-卸載-再加載的管土相互作用過程，其中虛線表示土作用力的邊界圈，上邊界指土的最大抗力，下邊界由最大吸力確定，土抗力和吸力表達式分別為：

Pu(z)=Nc(z/D)su(z)D

(6)

Pu-suc=-fsucPu(z)

(7)

式中：Pu(z)為海床抗力；Pu-suc為海床吸力；Nc(z/D)為承載因子，當z/D≥0.1時，取Nc(z/D)=a(z/D)b，其中a、b分別為模型無量綱系數，與溝槽寬度和立管直徑有關，如表1所示；當z/D<0.1時，取Nc=Nc(0.1)(10z/D)1/2，z為貫入深度，D為管直徑；fsuc為吸力因子；su為海床土的不排水抗剪強度，與管道的埋深有關，表達式為：

su(z)=su0+ρz

(8)

式中：su0、ρ分別為海床表面不排水抗剪強度和強度梯度。

文獻[6]確定了立管與海床接觸時三個階段曲線的數學表達式，圖2中橫坐標為無量綱參數ζ，通過對貫入深度z進行無量綱化得到：

ζ=z/(D/Kmax)

(9)

式中：Kmax為最大豎向剛度，本文取200。該曲線考慮土剛度退化，表現為上拔后再次貫入時抗力的衰減：

Pmax(z)=ERP(z)PIP(z)

(10)

式中：PIP(z)為初始貫入階段的抗力，ERP(z)可表示為：

ERP(z)=emin[0,-λrep+(z-zp=0)/(λsuczmax)]

(11)

式中：zmax為最大貫入深度，zp=0指土抗力為零時的最大貫入深度，λsuc為無量綱的吸力衰減因子，λrep為無量綱再貫入系數。

表1 a和b的取值Tab. 1 Value of a and b

圖2 典型土抗力-埋深曲線[6]Fig. 2 A typical resistance-penetration curve[6]

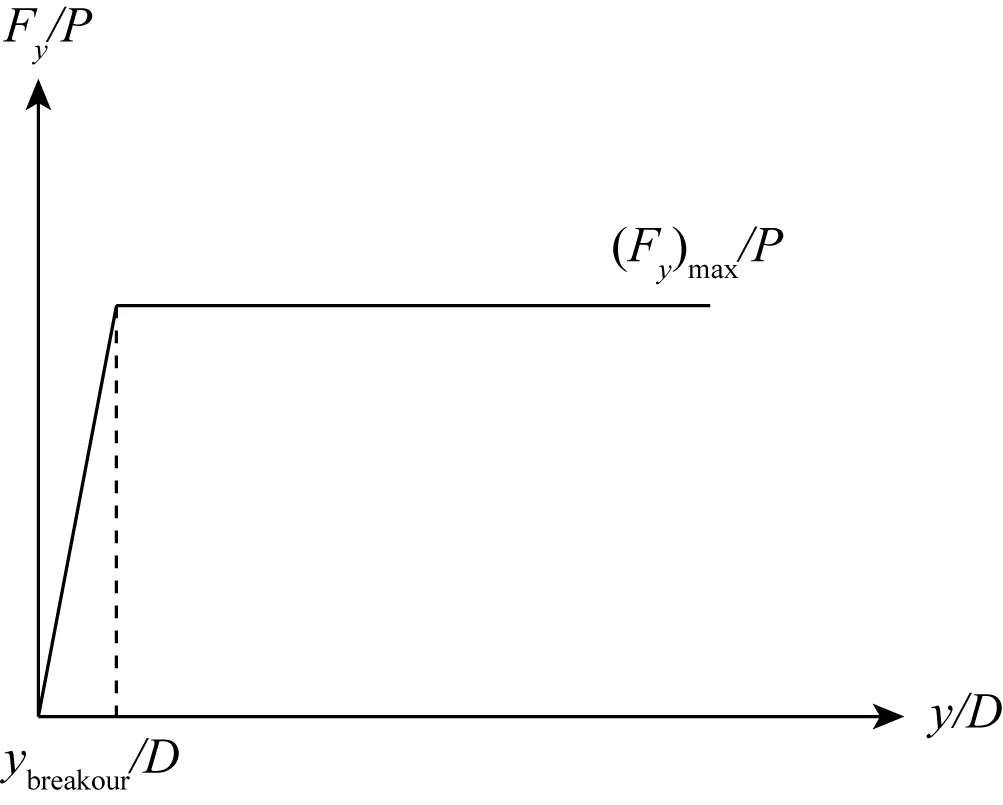
圖3 側向庫倫摩擦“雙線”模型[17]Fig. 3 Coulomb friction ‘bi-linear’[17] model in lateral direction

圖3為側向庫倫摩擦“雙線”模型，側向阻力Fy由豎向土抗力和摩擦系數確定，表達式為[17]：

Fy=-suAy

(12)

式中：y為立管的側向位移，su為土剪切強度，A為立管側向與土接觸面積。在OrcaFlex的摩擦模型中，側向庫倫摩擦力的變化區間為[-μP,μP]，管道在溝槽中的側向偏移區間為[-ybreakout,ybreakout]，則ybreakout可表示為：

ybreakout=μP/suA

(13)

式中：μ為摩擦系數，一般在0.2～0.8之間；P為豎向海床土抗力，與海床平面相切。

1.3 疲勞分析

S-N曲線又稱為應力-壽命曲線，常用來計算結構的疲勞問題，表達式為[18]：

logN=loga-mlogS

(14)

式中：a、m為由實驗確定的經驗系數，S為應力幅值，N為與應力幅值對應的循環次數。

通過應力集中系數及厚度修正系數對應力幅值S進行修正，修正后的表達式為：

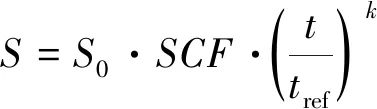
(15)

式中：S0為名義應力幅值；SCF為應力集中系數；t和tref分別為立管的實際壁厚和參考壁厚，參考壁厚取25 mm；k為厚度指權。

2 算例分析

2.1 SCR模型參數

以一根工作水深為1 500 m的SCR為研究對象，具體參數見表2。假設海床是水平的，分別選擇線彈性和非線性海床剛度模型，其中豎向非線性海床分低、中和高強度三種類型，海床側向剛度為11.52 kN/m/m2，吸力因子取0.2，吸力衰減因子取0.5，再貫入系數取0.55，摩擦系數取0.5。

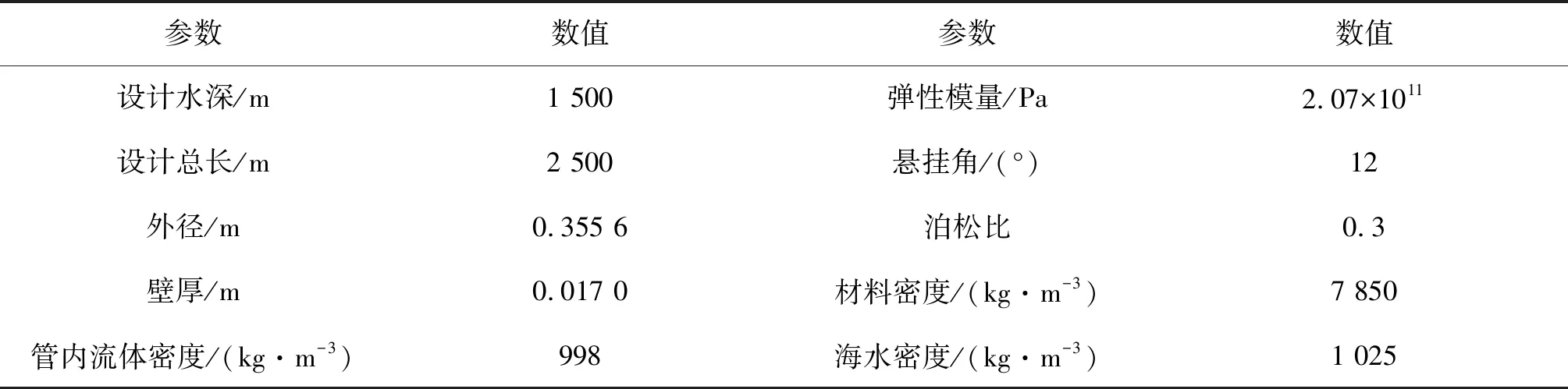
表2 鋼懸鏈式立管模型參數Tab. 2 Model parameters of SCR

2.2 計算工況

主要研究不同平臺的激勵運動方式、不同強度的海床模型對SCR觸地點動態響應和疲勞壽命的影響，共28個工況，選擇表3所示的10個計算工況進行對比分析。將立管劃分為柔性接頭、懸垂段、觸地段和流線段四個部分，這與現有研究中僅將平臺與SCR的連接作為鉸接來處理[12]更符合工程實際。根據需要每段選取的單位長度不同，總共劃分為880個單元。平臺激勵運動周期為16 s，運動幅值為2 m，波高為6 m，波周期為8 s，海面流速為1.07 m/s，每個工況分析時間為300個周期，時間步長為0.02 s。

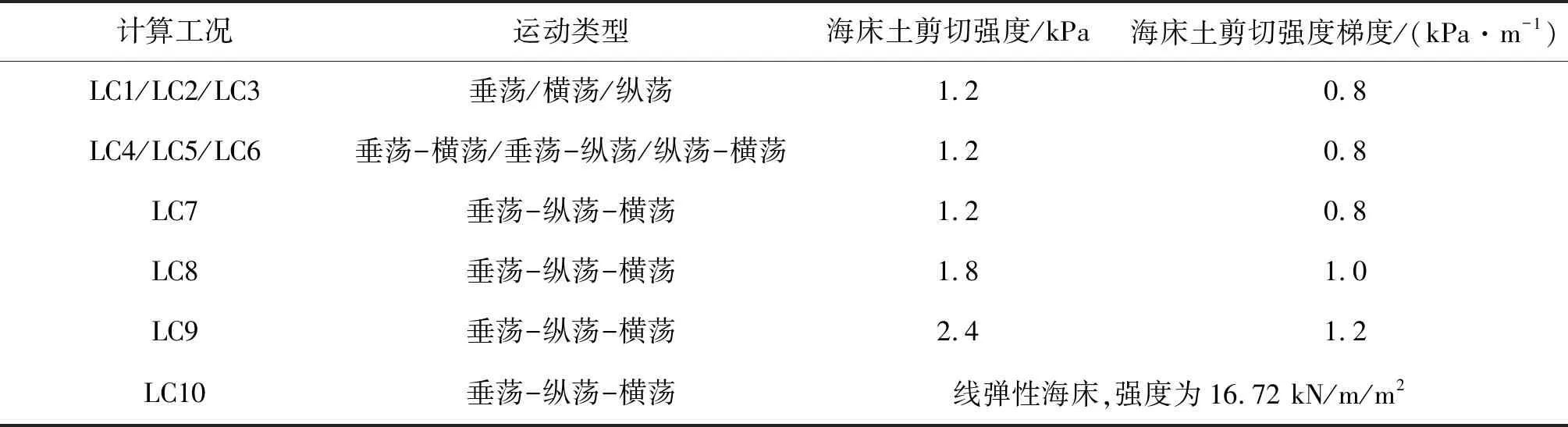
表3 計算工況Tab. 3 Calculate conditions

3 結果分析與討論

平臺不同形式的運動激勵下，分別得到立管觸地點的應力、位移以及貫入深度的變化情況；不同的海床強度對觸地點動態響應的影響分析；平臺運動和海床剛度模型對觸地點疲勞壽命的影響程度。

3.1 平臺運動的激勵

選用非線性低強度海床土，對平臺不同運動激勵下觸地點應力時程曲線、管土作用曲線、觸地區貫入深度進行對比分析。

3.1.1 觸地點應力

立管觸地點循環應力是發生疲勞破壞的關鍵因素，在LC1～LC7工況作用下，即立管與低強度非線性海床作用，觸地點位置在管長1 879 m左右，分別得到圖4所示的觸地點應力變化對比曲線。結果表明：1)一維運動時，垂蕩、縱蕩和橫蕩運動引起的觸地點應力幅值分別為49、12.4和2.2 MPa，應力幅值大小是導致立管疲勞損傷的關鍵因素，可見垂蕩運動對立管觸地點和頂端動態響應的影響最大，而橫蕩運動受海床側向阻力作用，其影響程度最小；2)二維運動激勵時，觸地點應力幅值分別為47.6、38.8和14.6 MPa，二維耦合運動在一定程度上減弱了垂蕩運動引起的動態響應；3)三維運動作用時，觸地點應力幅值為38 MPa，相對包含垂蕩二維耦合運動有所降低，但遠大于縱蕩和橫蕩。

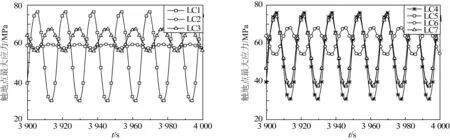
圖4 立管觸地點應力時程曲線Fig. 4 TDP stress time series under motion excitation of platform

為了驗證本文結論，與文獻[12]進行了對比分析，如圖5所示，選擇文獻[12]中工況LC2和本文工況LC7，對觸地點應力進行對比分析。由對比結果可知：同一海床強度和運動幅值下，垂蕩引起的觸地點應力幅值比三維運動大4.21 MPa，而且三維運動引起的觸地點應力振蕩周期明顯增加。疲勞損傷的產生原因主要是應力幅值和作用周期，幅值小周期長的循環應力將會降低結構的疲勞損傷，這與本文的結論是吻合的，即三維運動的耦合將會在一定程度上降低SCR觸地區的疲勞損傷，因此僅考慮平臺的垂蕩運動來預測立管的疲勞損傷是不準確的。圖6給出了LC7工況下觸地點土抗力隨相對埋深的變化曲線，體現了圖2所示的加載-卸載-再加載的整個作用過程及豎向海床剛度的退化現象，與文獻[12]的結果相比，更符合實際作用過程。

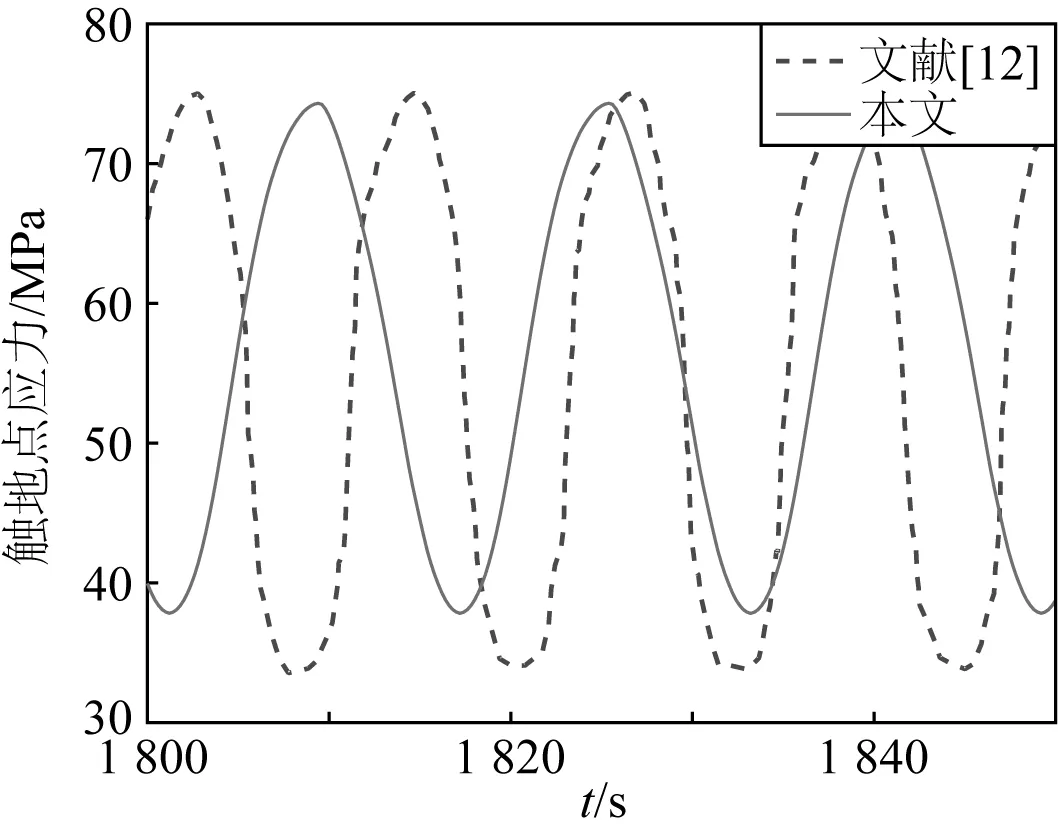
圖5 觸地應力時程曲線對比Fig. 5 Comparison of the TDP stress time series of SCR

圖6 觸地點土抗力隨相對埋深的變化曲線Fig. 6 Resistance-penetration curve of TDP

3.1.2 立管觸地區的最大貫入深度

由于平臺運動特別是垂蕩運動會引起管土的往復作用，將在海床表面形成溝槽。為研究運動形式對溝槽大小的影響程度，基于非線性低強度海床和側向海床的阻力作用，分別由一維、二維和三維運動作用300個周期后，獲取立管最大貫入深度時的位型圖，如圖7所示，其中左圖為LC1～LC3工況，右圖為LC4～LC7工況。表4列出了不同運動方式在海床表面產生的最大貫入深度和相對深度值。由表可知：短期管土作用下，立管的最大貫入深度均小于0.3倍管徑，垂蕩運動的影響最大，而耦合運動時溝槽深度略有減小。

圖7 立管最大貫入深度時的位型Fig. 7 Configuration of the maximum penetration depth of riser

表4 不同運動類型下SCR最大貫入深度對比Tab. 4 Comparisons of the maximum penetration depth under different excitation motion

3.2 海床模型的影響

為了研究海床模型對觸地區動態行為的影響程度，選擇LC7～LC9和LC10工況進行對比分析，其中線彈性海床與低強度非線性海床的強度相當。四種工況下觸地點的位置有變化，分別位于管長1 879、1 883、1 884和1 878 m處。圖8為四種工況下的觸地點應力時程曲線，由圖可知：LC7和LC10工況作用下為高應力的低幅值循環，而LC8、LC9工況下為低應力的高幅值循環，幅值大小是引起疲勞損傷的關鍵因素之一。圖9為土抗力隨平臺運動的時程變化曲線對比，非線性海床模型作用下土抗力變化幅值遠大于線彈性海床。而貫入深度則相反，采用線性海床時，立管貫入深度明顯較大，如圖10所示。圖11為立管的彎矩分布圖，兩種海床模型作用下，得到彎矩分布圖基本一致，也驗證兩種海床模型的強度相當。可見選擇線彈性海床模擬海床作用是不準確的，與實際差別較大，特別是觸地區的應力和溝槽大小。

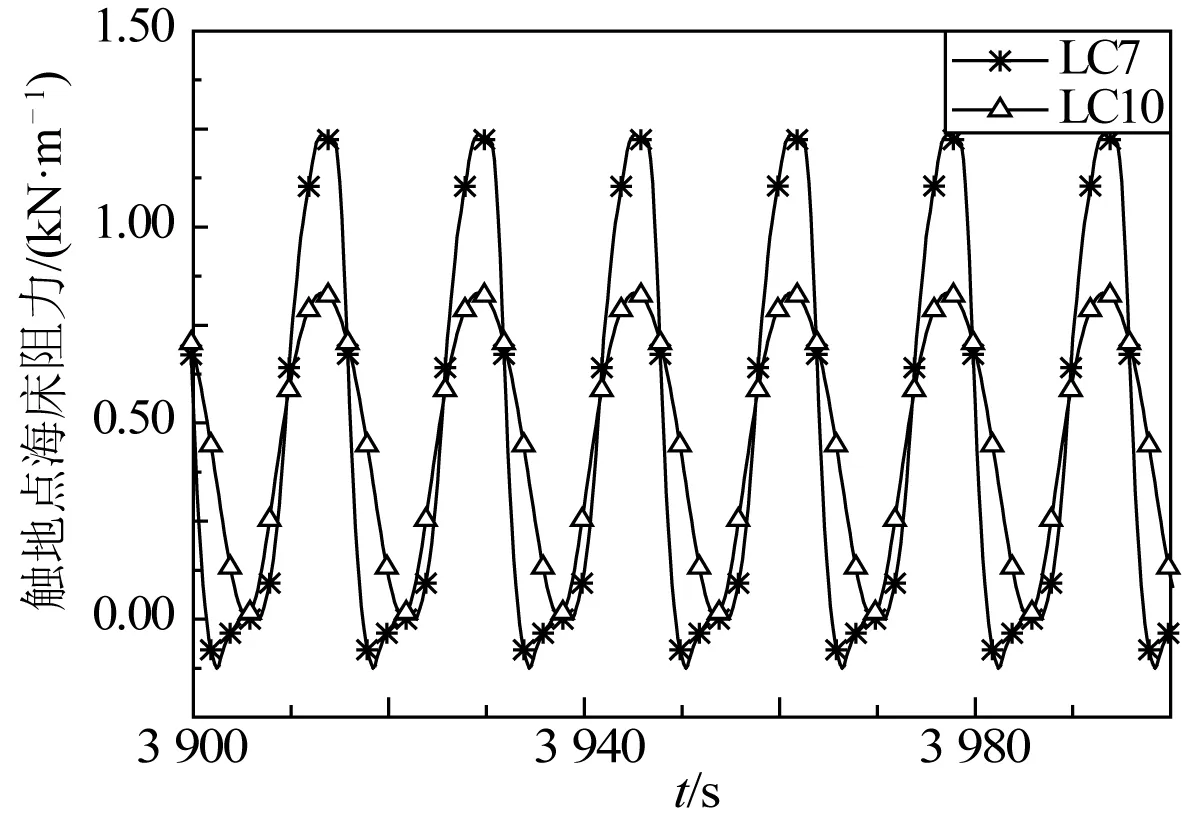
圖9 立管觸地點海床抗力時程曲線Fig. 9 Time series of seabed resistance at TDP

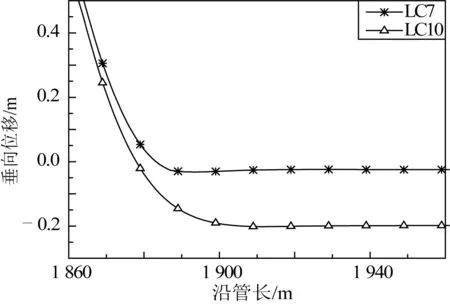
圖10 不同海床模型作用下立管觸地區貫入深度Fig. 10 Progressive penetration with different seabed models

圖11 立管彎矩分布Fig. 11 Bending moment distribution of SCR

如圖12所示，LC7、LC8和LC9工況下立管觸地點側向位移，隨著海床強度的增加，幅值逐漸減小，變化趨勢相似；圖13為立管觸地點豎向位移的時程曲線，隨海床強度的增加，位移幅值降低，貫入深度變淺，在接近海床表面時，豎向位移曲線變得比較平坦。

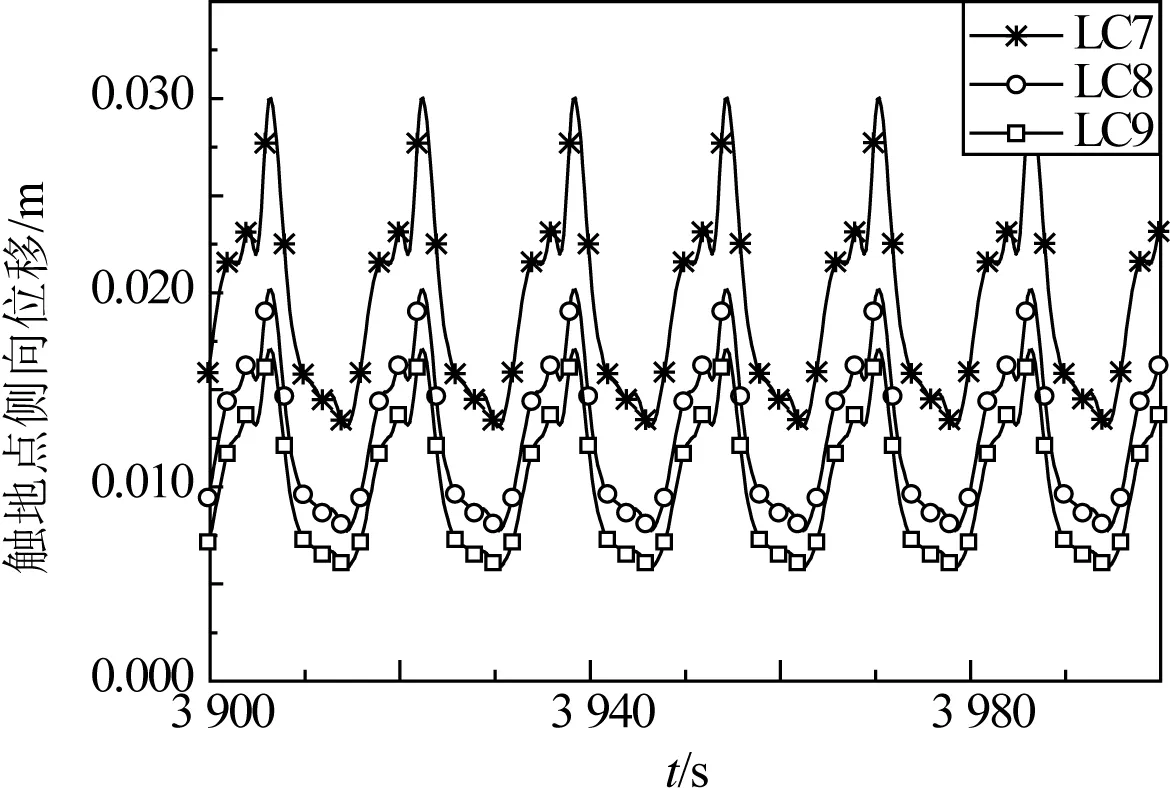
圖12 立管觸地點側向位移Fig. 12 Lateral displacement of TDP

圖13 立管觸地點豎向位移Fig. 13 Vertical displacement of TDP

3.3 疲勞分析

根據立管的動力響應分析，運用S-N曲線對立管進行疲勞分析，分兩種情況：1)研究不同運動形式對立管觸地區疲勞壽命的影響，選擇LC1和LC4～LC7工況，如圖14所示，垂蕩作用下立管疲勞壽命最低為76年，也說明垂蕩運動是影響立管觸地區疲勞壽命的關鍵因素，而三維運動作用下即LC7工況，立管疲勞壽命則提高至134年，縱蕩與橫蕩運動的影響可忽略；2)研究不同海床模型對立管觸地區疲勞壽命分布情況的影響，LC7～LC10工況，如圖15所示，高強度非線性海床作用時，立管觸地點的疲勞壽命最低為95年。線彈性海床作用下，立管觸地區的疲勞壽命明顯偏高，因此簡化計算時，選用線彈性海床進行模擬管土作用是不安全的。由圖示可知，SCR觸地點處的疲勞壽命最小，并向兩側迅速增加，該區域控制著立管的使用壽命，應在設計和工程應用中予以加強，其中最小疲勞壽命對比結果見表5。

表5 觸地區疲勞壽命對比 Fig. 5 Comparison of fatigue life at TDP of SCR

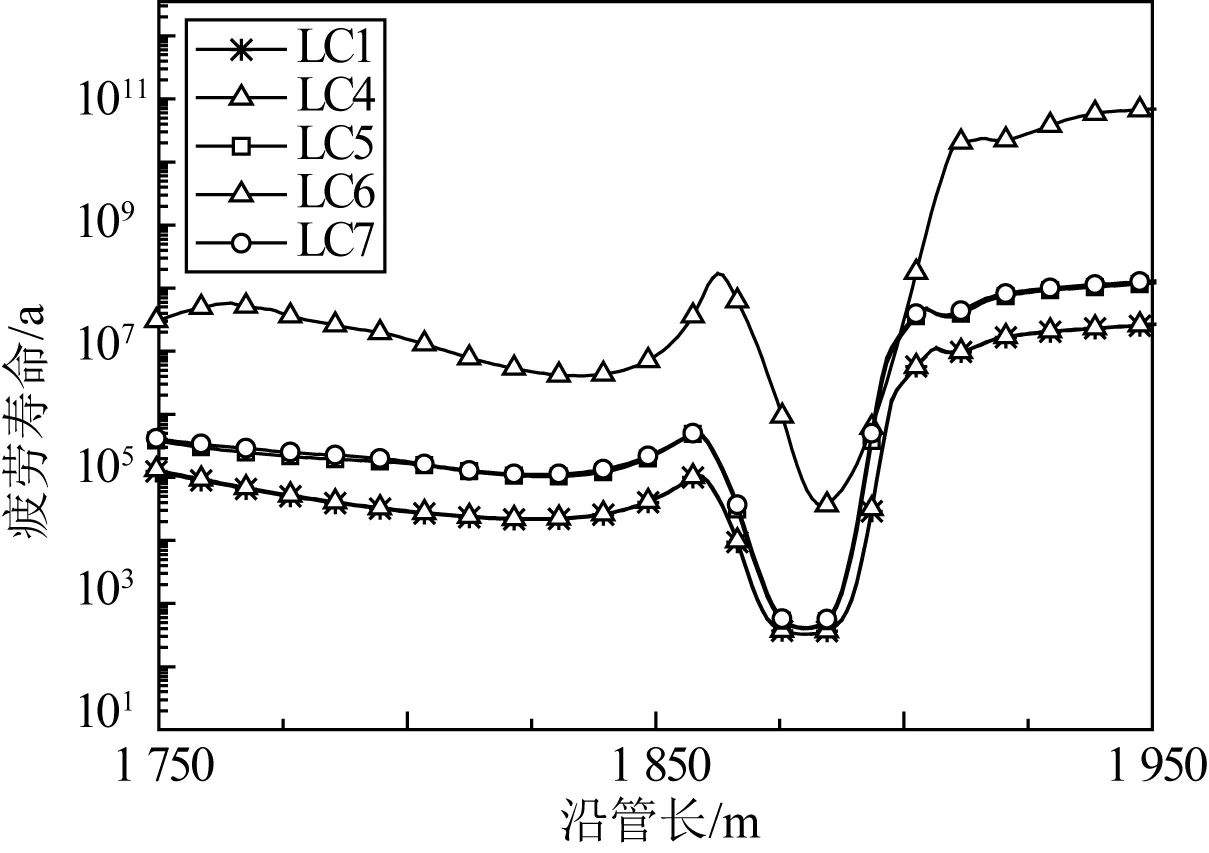
圖14 不同平臺運動激勵下立管疲勞分布Fig. 14 Fatigue life in TDZ under different excitation motions

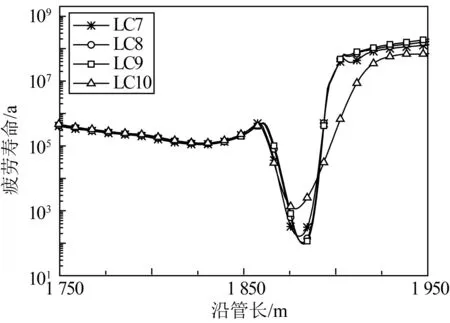
圖15 不同海床強度下立管疲勞分布Fig. 15 Fatigue life in TDZ under different seabed strength

4 結 語

基于豎向非線性海床模型和側向庫倫摩擦模型，考慮海床土豎向剛度的退化，建立SCR與平臺的三維分析模型，研究平臺運動、海床剛度模型對SCR觸地區動態行為、疲勞損傷的影響，得到如下結論：

1) 平臺垂蕩運動對立管觸地區的應力幅值、貫入位移和疲勞損傷的影響最大，縱蕩運動次之，而橫蕩運動受側向海床土阻力作用，其影響最小，從最小疲勞壽命看，垂蕩運動與縱蕩-橫蕩耦合運動不在一個數量級；

2) 將平臺運動耦合之后，在一定程度上使立管觸地區的動態響應降低，因此僅考慮垂蕩運動的情況偏于保守；

3) 在海床模型中考慮側向阻力的影響，從計算結果可知，側向阻力使得平臺橫蕩運動對立管動力響應和疲勞壽命的影響降低，目前以管土豎向作用為主的研究結論同樣偏于保守；

4) 海床剛度模型不同，對立管觸地區動態響應的影響主要體現在：隨海床強度和應力幅值的增加，貫入位移和疲勞壽命逐漸減小。特別是選擇線彈性海床與實際差別較大，在貫入位移明顯較大時，所得的動態響應較小，疲勞壽命較高，對實際工程不安全。

5) 在豎向非線性海床剛度模型中，考慮了土剛度退化現象，更符合海床軟土的實際力學特性。