基于GPU加速的Boussinesq類波浪傳播變形數值模型

孫家文，朱 桐，房克照，劉忠波

(1. 大連理工大學 海岸和近海工程國家重點實驗室 DUT-UWA海洋工程聯合研究中心，遼寧 大連 116024； 2. 國家海洋環境監測中心，遼寧 大連 116023； 3. 大連海事大學 交通運輸工程學院，遼寧 大連 116026)

作為一種典型的水波方程，Boussinesq類方程同時考慮色散性與非線性特征，能較準確地描述近岸海域波浪的傳播演變過程，再現波浪在傳播過程中出現的折射、繞射、散射、反射、淺水變形等物理現象。因此，Boussinesq方程被廣泛應用于近海區域波浪的數值計算[1-2]。Peregrine[3]于1967年推導了適應變水深的二維Boussinesq方程，該方程被稱為經典Boussinesq方程。但是該方程僅含有弱非線性和弱色散性項，難以適應大水深及非線性較強的問題。針對這類問題，Madsen和S?rensen[4]于1992年推導了二維擴展型Boussinesq水波方程(后稱MS92方程)。該方程在動量方程中加入具有特定系數的三階偏導數項，使得方程的色散性提高了一階。因為MS92方程形式簡單，又具有較好的色散性，得到廣泛應用。

以Boussinesq方程建立的時域數值模型屬于相位解析模型，為保證計算精度則需要較高的時間和空間分辨率。研究表明，單純使用有限差分方法求解這類方程易產生高頻數值震蕩，影響計算的穩定性，通常需要采用具有耗散性質的光滑器以滿足穩定性的需求[5-6]。利用有限體積法求解Boussinesq方程一定程度上可解決上述問題[7-8]。求解時，采用有限體積方法計算對流項，剩余項則采用有限差分方法求解，這一方式經過驗證已經取得了較好的效果[9-10]。但是利用有限體積法離散對流項時，需要對界面左右變量進行狀態重構和數值通量求解，過程較為復雜，耗時較高，當網格數目較多時更會大幅度增加計算時間。若想同時保證計算的精確性與高效性，單個主機的計算性能已經很難滿足要求。采用主機與圖形處理器相結合的方式搭建高性能計算平臺是解決辦法之一。迄今，眾多CPU上的算法已成功移植到GPU上，計算效率得到了明顯提升[11-12]。近兩年，GPU已經開始使用到Boussinesq類模型的數值計算當中。Tavakkol[13]開發了一種基于GPU加速的Boussinesq類波浪模擬軟件，不僅能提高計算效率，而且交互性強，提供了包含真實化渲染等很多可視性選項。Kim等[14]使用CUDA FORTRAN語言實現了Boussinesq方程模型的GPU并行化，計算效率相比CPU模型明顯提升，最大加速比(CPU時間/GPU時間)可達20以上。GPU具有高并行性與強大的數據處理能力，能很好地解決當下數值模擬中網格數量多和計算效率低的問題。將來，采用GPU的海洋數值模型是海洋研究發展的重要方向之一。

利用CUDA C語言搭建基于GPU加速的Boussinesq類波浪傳播變形數值模型，并模擬一系列經典工況，把所得的結果與解析解及CPU模型的模擬結果相比較，以驗證模型的計算精度。除此之外，還比較了同種工況采用GPU模擬與CPU模擬的運算效率，得到了計算效率與網格數目之間的關系。

1 數學模型

1.1 控制方程

MS92方程的守恒形式如下[15]：

Ut+F(U)x+G(U)y=S(U)

(1)

式中：U為變量矢量，F和G為x與y方向上的通量矢量，定義為：

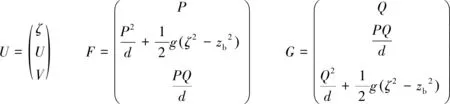
(2)

其中，

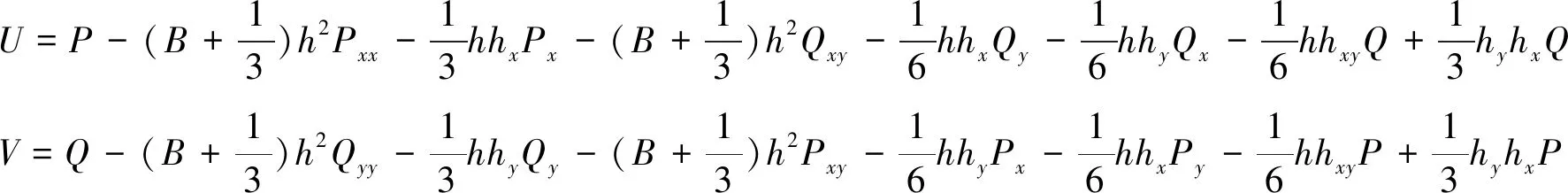
(3)

式中：d=η+h為總水深，η表示自由波面，h為靜水水深，P和Q分別表示x和y方向上的速度通量(P=du和Q=dv，u、v分別表示x、y方向的水深平均速度)，B為色散性參數，取1/15。為實現海床變化和海岸水-陸動邊界存在時高精度有限體積方法的和諧解，引入水位ζ=zb+d。式(1)中S為源項，可將其分成三個組成部分，分別為水底坡度項Sb、水底摩擦項Sf和色散項Sd，如下：

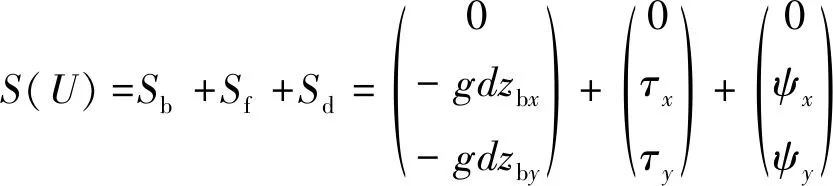
(4)

式中：色散項為：

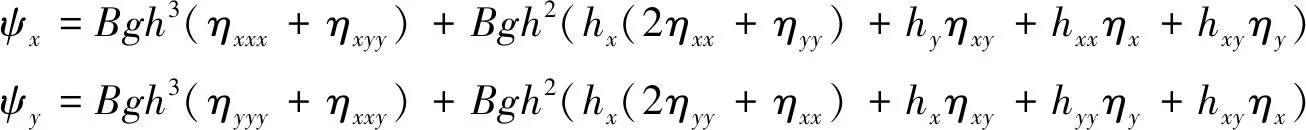
(5)

水底摩擦項：

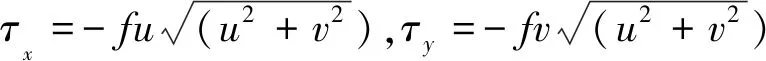
(6)

式中：f為底摩擦系數，取值范圍為0.000 1～0.01，本文所有工況計算均未考慮海床摩擦。

1.2 方程空間離散、時間積分與模型邊界條件

采用矩形網格單元，將計算域在空間、時間上均勻劃分單元網格，波面η和速度u均定義在控制體中心。為了提高空間精度，采用四階高精度狀態差值方法(MUSCL)對界面左右變量進行重構，應用重構后的界面變量進行通量計算。模型的時間積分采用具有TVD性質的三階龍格-庫塔方法[16]。為保證計算收斂，時間計算步長由Courant-Friedrichs-Lewy(CFL)穩定性限制條件確定：

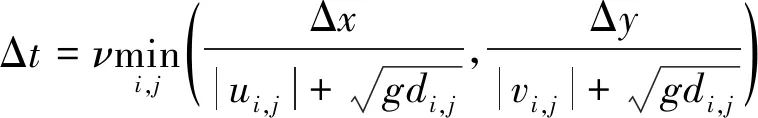
(7)

式中：ν為常數，這里取ν= 0.25。

對于文中計算工況，波浪通過給定初始條件或內部造波方法產生，計算域末端均為固壁邊界，視情況不同在固壁前設置海綿層以吸收波浪能，以有效降低數值計算中的二次反射[15]。

2 GPU并行計算簡介

在CUDA的并行計算模型中，CPU作為主機端，負責運行主程序并在運行過程中調用核函數。GPU作為設備端，主要進行線性化的并行計算。在設備端運行的函數被稱為核函數。每個核函數對應的線程均以線程網格(grid)的形式存在，線程網格又被分成多個線程塊(block)，每個線程塊又由大量的線程(thread)組成。文中模型采用每個線程塊1 024個線程的分配方案。

由于GPU無法直接讀寫內存中的數據，因此在核函數運行先需要初始化數據并將其由主機端傳遞到設備端的全局存儲器中；之后，各個線程塊會分配到不同的GPU大核 (Streaming Multiprocessors，簡稱SM)上，線程塊上的不同線程交給GPU大核上不同的CUDA核心 (Streaming Processor，簡稱SP)來執行，從而達到并行運算的效果，如圖1所示。為充分發揮GPU計算效率，在程序設計時，將主循環中計算耗時較重的模塊，如狀態重構、通量計算、時間積分等設計為核函數，在設備端運行。模型的初始化參數以及輸入輸出等模塊在主機端部署。設備端和主機端之間通過CUDA C提供的內置函數(memcpy)進行數據傳遞，模型計算流程見圖2。

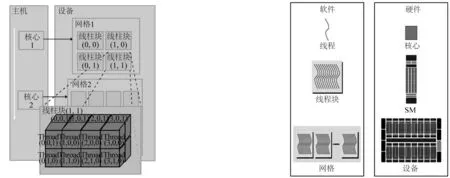
圖1 CUDA編程模型Fig. 1 CUDA programming model

3 數值驗證

針對所建立的GPU模型，通過幾個典型工況的數值模擬分別對其進行驗證。其中工況一為常水深孤立波的長距離傳播問題；工況二為規則波跨越潛堤傳播；工況三為封閉方形水池中的水面晃動；工況四為波浪在橢圓形淺灘上的傳播。

3.1 孤立波在常水深水槽中的傳播

在本工況中，x方向計算域長度為409.6 m，靜水水深h0為1.0 m，在計算域內給出孤立波解析解作為初始條件，波高H=0.6 m，孤立波從計算域的左側向右側傳播，初始時刻波峰位于x0=25 m處，網格尺寸Δx=0.2 m，忽略底摩擦的影響，且計算域邊界處均采用固壁邊界條件。圖3給出了模擬的孤立波在t=0，10，20，30，40，50，60，70和80 s時的波面狀態。從圖中可見，經過長距離的傳播，孤立波的波形和波高值均保持穩定，幾乎未發生變化，說明數值離散正確，未引入額外的數值耗散和數值彌散。圖4為時間t=80 s時，模型計算結果與解析解的比較，可以看出兩者高度吻合，說明模型具有較好的精確性。

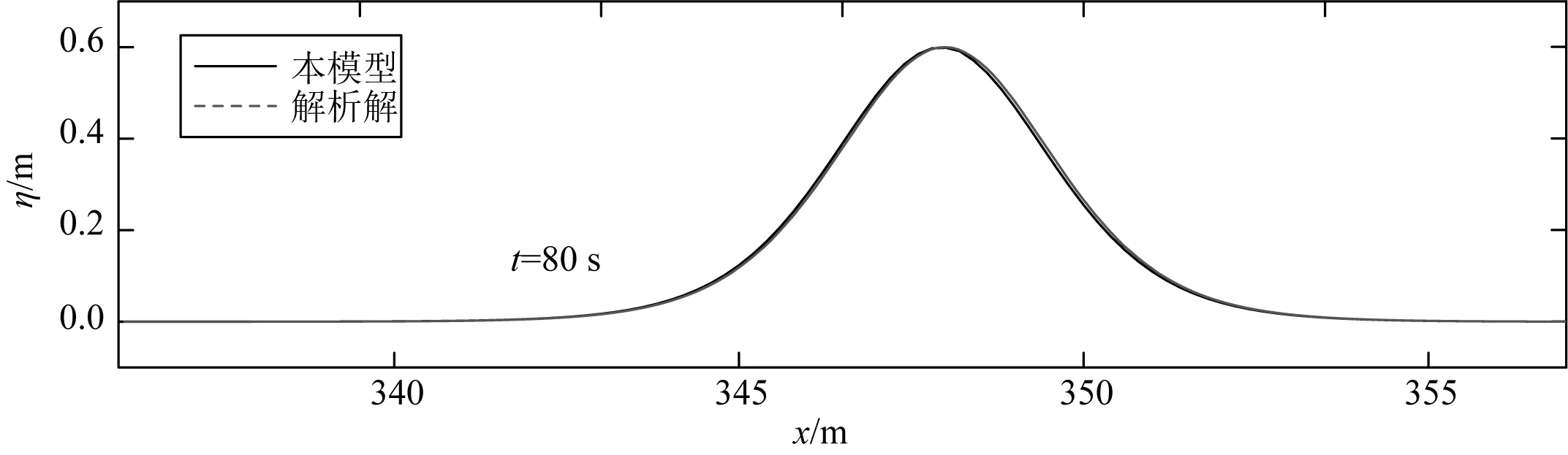
圖4 t= 80 s時數值模擬結果與解析解的對比Fig. 4 Comparison of simulated and analytical surface profiles at t=80 s

3.2 規則波在潛堤海床上的傳播

規則波跨越水下潛堤傳播是非常復雜的波浪演化過程，涉及波浪的變淺、高次諧波產生釋放等，該類試驗被用來檢驗各類數值模型的色散性和非線性等綜合性能。采用Dingemans[17]的規則波跨越潛堤傳播的試驗來對數值模型進行檢驗，試驗海床設置如圖5中所示，海床兩端設置1.5倍波長海綿層吸收波浪，造波機在x= 0 m處，平底處靜水水深為0.4 m，梯形壩的坡腳位于x=6.0 m處，梯形壩頂端長為2.0 m，距離靜水面0.1 m，梯形潛堤前坡坡度為1∶20，后坡坡度為1∶10，根據Dingemans[17]的試驗，在計算域內設置10個浪高儀，位置分別為x= 2，4，10.5，12.5，13.5，14.5，15.7，17.3，19和21 m。入射波波高H=0.02 m，周期T=2.02 s，計算網格長度為Δx=0.025 m。

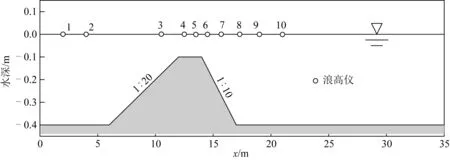
圖5 規則波跨越潛堤傳播試驗布置Fig. 5 Experimental setup of regular waves propagation over submerged bar

圖6給出了10個浪高儀位置上數值模擬結果與試驗數據和CPU模型模擬結果的對比。如圖6所示，規則波跨越堤頂傳播過程中，水深變淺，波浪的非線性增強，高次諧波產生，波形發生明顯變化，潛堤前以及堤頂位置處波面的數值計算結果與Dingemans的試驗數據吻合程度高，說明GPU模型能夠準確模擬規則波的傳播及跨越潛堤時的波浪狀態。堤后伴隨水深的增加，各次諧波變成自由波，計算結果與實測值存在一定誤差，這主要是方程捕捉高次諧波的色散性和非線性均不夠造成的。整體來看，GPU模型與CPU模型的計算結果高度一致，驗證了GPU模型的正確性。

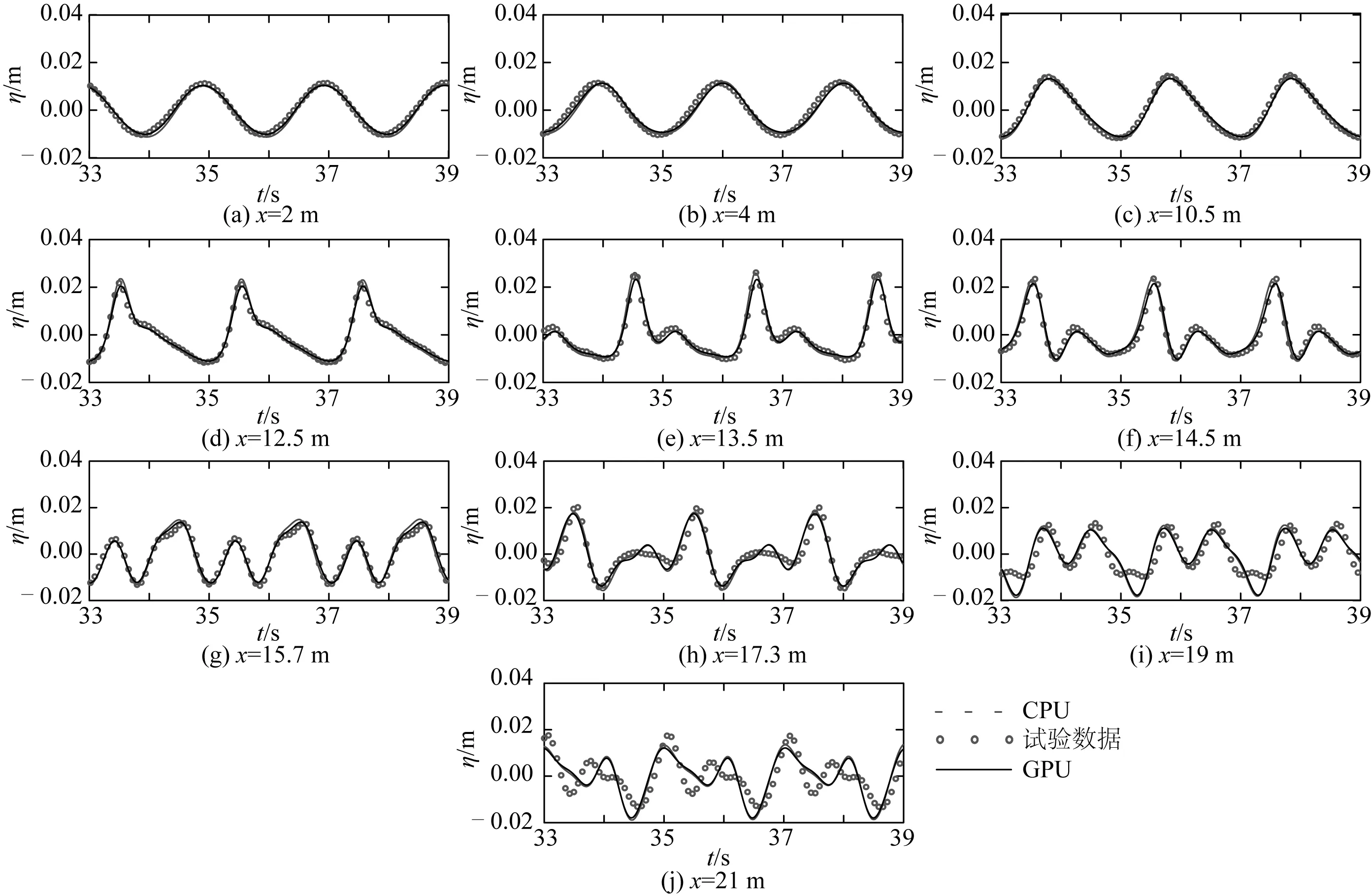
圖6 規則波跨越潛堤傳播各浪高儀處的波面時間序列Fig. 6 Time series of surface elevations for regular waves passing over a submerged bar

3.3 封閉方形水池中的水面晃動

為了驗證模型精度以及對全反射邊界的處理能力，對封閉方形水池中液體晃動進行了模擬。數值水池為正方形，尺寸為7.5 m×7.5 m，水深h= 0.45 m。水池四邊為全反射直墻且與x、y軸平行，坐標原點位于水池左下角。網格尺寸Δx=Δy=0.058 593 75 m。初始波面為Gaussian形，即：

η0(x,y)=H0exp{-2[(x-a)2+(y-b)2]}

(8)

式中：a=b=3.75 m，H0=0.045 m。

圖7給出了波面在一段時間后的分布情況。如圖7所示，在t= 2 s時，波面關于x軸和y軸完全對稱。經過比較長時間的傳播后，在t=20 s時，對稱性仍能很好地保持，說明模型離散和數值計算正確。

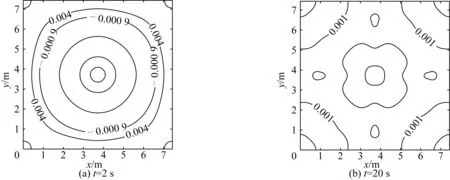
圖7 t=2 s與t=20 s時波面分布Fig. 7 Free-surface contours at time t=2 s and t=20 s

圖8給出了H0= 0.045 m時水池角點處和中心點處自由表面計算結果和線性理論結果的比較。波浪傳播過程中前20 s內的非線性相對較弱，因而基于GPU加速的弱非線性Boussinesq數值模型與解析解結果基本一致。在后20 s內，伴隨邊界反射疊加，波浪的非線性增強，組成波成份增多，超出了方程本身非線性和色散性使用范圍，導致二者存在一定的誤差。

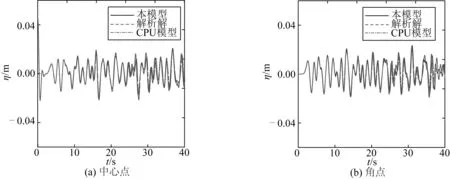
圖8 H0=0.045 m時波面時間過程與線性理論計算結果比較Fig. 8 Comparison of time series of free surface elevation between numerical and theoretical results for H0=0.045 m

3.4 波浪在橢圓形淺灘上的傳播

為了檢驗模型模擬復雜地形上波浪傳播變形的能力，對Berkhoff等[18]所做的橢圓形淺灘上的波浪折、繞射物理模型試驗進行了數值模擬。在模擬中，計算區域長30 m，寬20 m，具體試驗地形如圖9所示。

模擬波浪入射波高為H0=0.046 4 m，周期T=1 s，在x=3 m處沿x軸正向入射。上下兩邊界(y=0 m和y=20 m)為全反射邊界，左側海綿層寬度為2 m，右側海綿層寬度為3 m。網格數目為512(x方向)×256(y方向)=131 072。模型運行時間為40 s。

將GPU模型計算結果與Tonelli和Petti[8]計算結果進行了對比，見圖10。可見，本模型的數值計算結果與Tonelli和Petti[8]所得結果基本一致，說明本模型可以較好地模擬波浪的折射和繞射等現象。

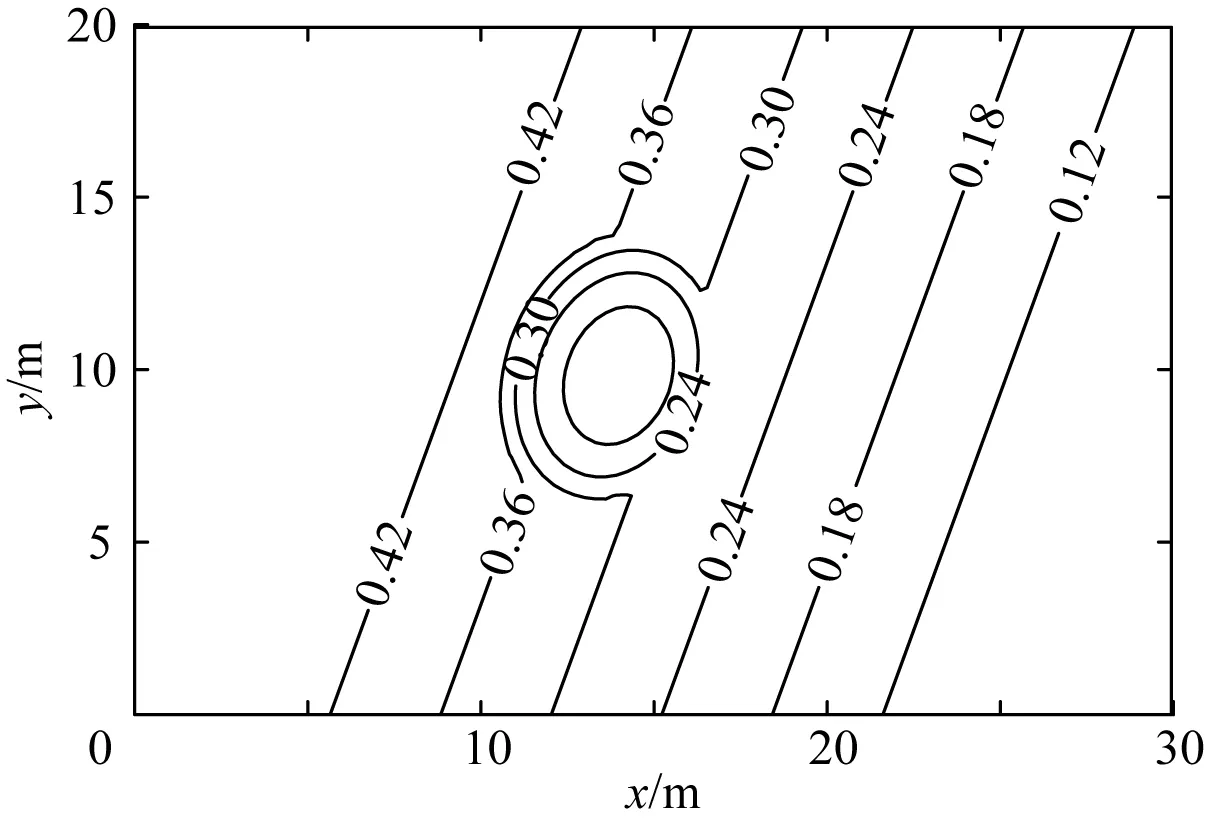
圖9 試驗地形圖(Berkhoff等[18])Fig. 9 Topographic map of experiment (Berkhoff, et al [18])

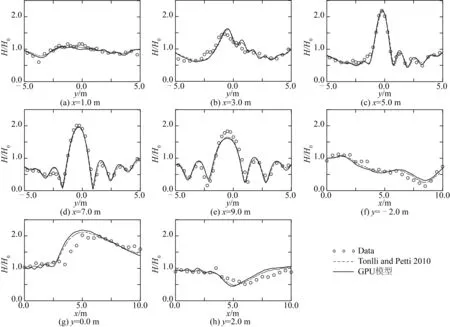
圖10 GPU模型計算波高與試驗數據和他人結果比較Fig. 10 Comparisons of normalized wave height from GPU model, data and other simulation

4 GPU并行模型加速性能分析

本文計算使用專業圖形加速卡Tesla k20進行，為了對比也使用CPU模型進行了計算。

具體設備參數和開發平臺如下：

CPU：Intel i5 8500，主頻3.0 GHz，含6個CPU核心。

GPU：專業圖形加速卡Tesla k20，含2 688個流處理器，主頻732 MHz，單精度浮點性能3.95 Teraflops，顯存5.2 GHz 6GB，帶寬250 GB/s。

開發平臺：Intel Complier Visual studio 2015，CUDA 8.0。

利用同一臺設備分別使用GPU模型與CPU模型進行計算，統計計算時間，并計算出加速比(CPU模型計算時間TC與GPU模型計算時間TG之比)，具體結果見表1。從表1可知，隨著網格數增加，加速比穩定提高。同時，不同的工況中的加速比一般不同，其中封閉方形水池的水面晃動所達到的加速比最大，計算效率的提升最為明顯，最大加速比可達12.72。綜合來看，GPU并行模型的確對計算效率有很明顯的提升。

Kim等[14]發展的GPU類Boussinesq模型加速比可達20，高于本文建立模型，可能是如下原因所致：1)圖形處理器不同，本文選用的圖形處理器是NVIDIA GeForce Tesla k20，Kim等選用的是NVIDIA GeForce GTX TITAN Z；2)編程框架不同，本文的編程語言是CUDA C，而Kim等選擇的是CUDA FORTRAN；3)計算工況不同，工況的差異會影響加速比，這在本文中已經得到了證明；4)算法不同，不同的算法由于數據讀取方式的不同，會對計算效率有著較大影響。

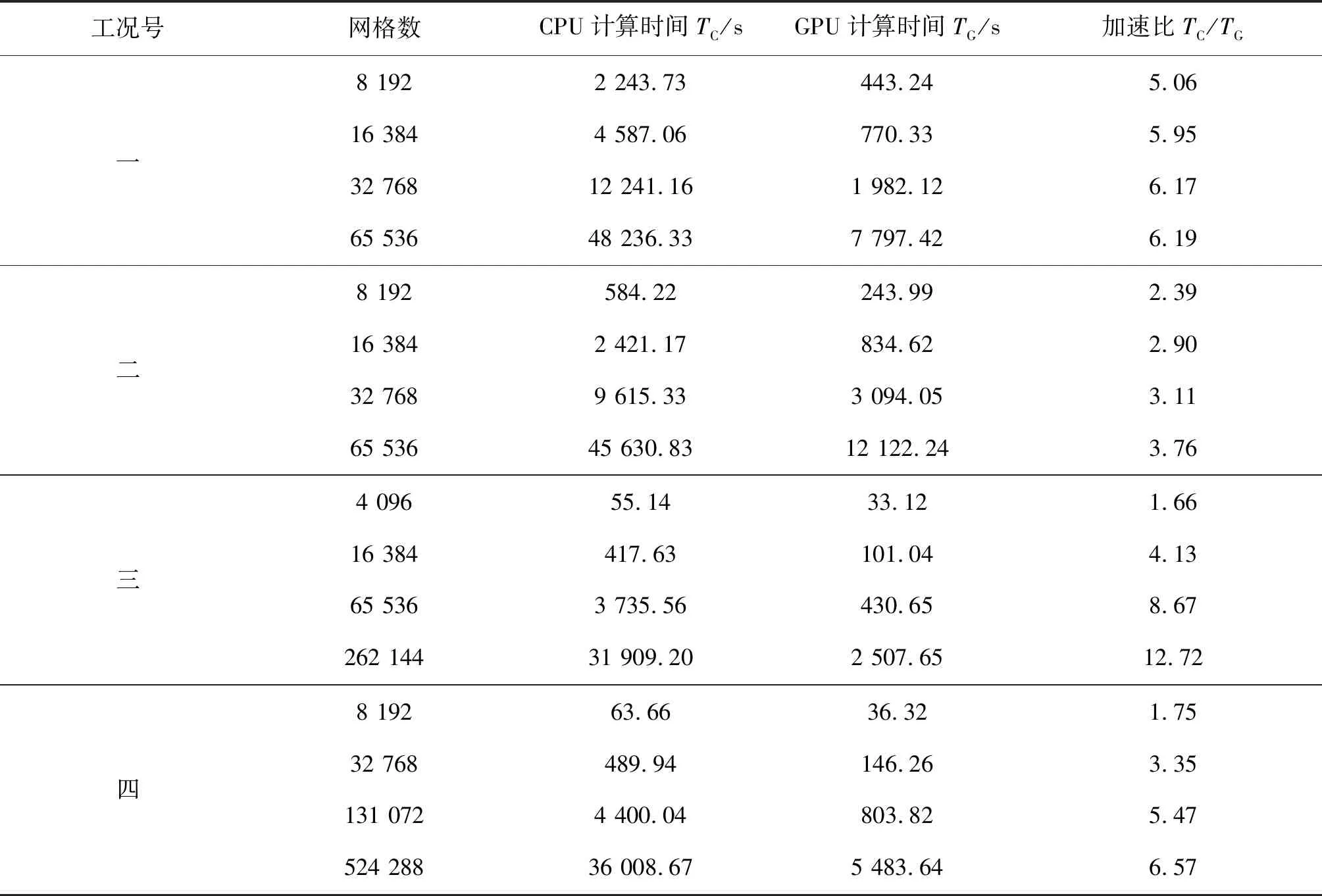
表1 各工況CPU模型與GPU模型計算效率比較Tab. 1 Computational efficiency comparison between CPU model and GPU model

5 結 語

利用CUDA C語言與圖形處理器(GPU)實現了Boussinesq模型的并行化。采用有限差分與有限體積的混合格式來求解方程。在計算過程中，通過把較為復雜的計算任務分配到GPU上分塊并行處理，從而實現大大提升計算效率的目的。將本模型的計算結果與CPU模型上的計算結果和模型本身的解析解相比較，所得結果基本一致，驗證了本模型計算的正確性。同時對本模型與CPU模型的計算效率進行了對比。通過比較發現，本模型對計算效率有很明顯的提升，文中工況的最大加速比可達12以上。

進一步的研究將圍繞不同圖形處理器設備加速性能、并行優化以及實際應用方面展開。