基于Newton法優化ARMA模型參數的船舶升沉運動預測研究

唐 剛，姚小強，胡 雄

(上海海事大學 物流工程學院，上海 201306)

船舶在海上作業時受到海浪的影響，會有明顯的橫搖、縱搖和升沉運動。目前，很多船舶己經具備動力定位系統，船舶的橫搖、縱搖運動得到較好的控制，而升沉運動的補償則需要通過波浪補償裝置來實現，但由于波浪補償裝置存在明顯的時延問題，嚴重影響船舶運動的補償精度和穩定性[1]。為了減小系統響應的時間滯后，通過對船舶的升沉運動進行預報，提前控制船舶的運動姿態，不僅能解決波浪補償系統的時延問題還能提高船舶在海上作業的安全性及效率，在軍事和民用領域具有重要價值。

船舶運動姿態預測方法主要分為頻域方法和時域方法，頻域方法主要有統計預報法和卷積法等[2-3]，但這些方法很難得到精確的響應核函數和波高測量函數，且運算速度較慢，因此頻域方法在實際應用中逐漸消失。時域方法主要有艏前波法、卡爾曼濾波法和時間序列法等[4-7]，時域法通過船舶運動姿態的歷史數據建模，預測未來較短時間內船舶的運動狀態，預測精度較高且計算速度快，因此常用于工程實際中。

時間序列分析法對波浪補償的時延具有較好的預測效果，且在線計算量小，實時性較好，同時對干擾和丟包等因素具有良好的魯棒性。Peng等[8]使用自回歸滑動平均(ARMA)模型對大型船舶姿態運動進行建模和預報，利用AIC準則確定ARMA模型的階數，縮短了船舶運動預報的計算時間并解決了ARMA 模型階數選擇的在線估計問題。Wei等[9]基于ARMA模型預測艦載直升機平臺的廣義升沉運動(橫搖、縱搖以及升沉方向的耦合運動)，使用阻尼遞歸最小二乘(DRLS)算法估計ARMA模型的參數，仿真結果表明ARMA模型可以較準確對艦載直升機平臺的廣義升沉位移進行多步預測。

當波浪補償系統具有隨機噪聲時，ARMA模型的參數估計容易漂移并且不穩定。因此，引入Newton法[10]優化ARMA模型參數，將模型的殘差平方和作為目標函數，通過反復迭代模型參數初值，使得模型的殘差平方和為極小值，仿真結果表明使用Newton法優化ARMA模型參數可以提高船舶升沉運動的預測精度。

1 加速度信號的采集與處理

1.1 升沉運動加速度信號采集

船舶升沉運動加速度信號是基于慣性測量單元(IMU)采集所得，IMU由加速度傳感器和陀螺儀組成，加速度傳感器可以用于測量船舶橫蕩、縱蕩以及升沉運動的加速度信號，陀螺儀可以用于測量船舶的橫搖、縱搖以及艏搖的角速度信號。將其安裝在船舶的船舶重心位置，設置采樣頻率為100 Hz，采集不同海況下船舶升沉運動的加速度信號。本文使用的仿真數據為船舶在二級海況、三級海況和四級海況[11]下航行的三組加速度信號{zt}，部分觀測數據見表1。

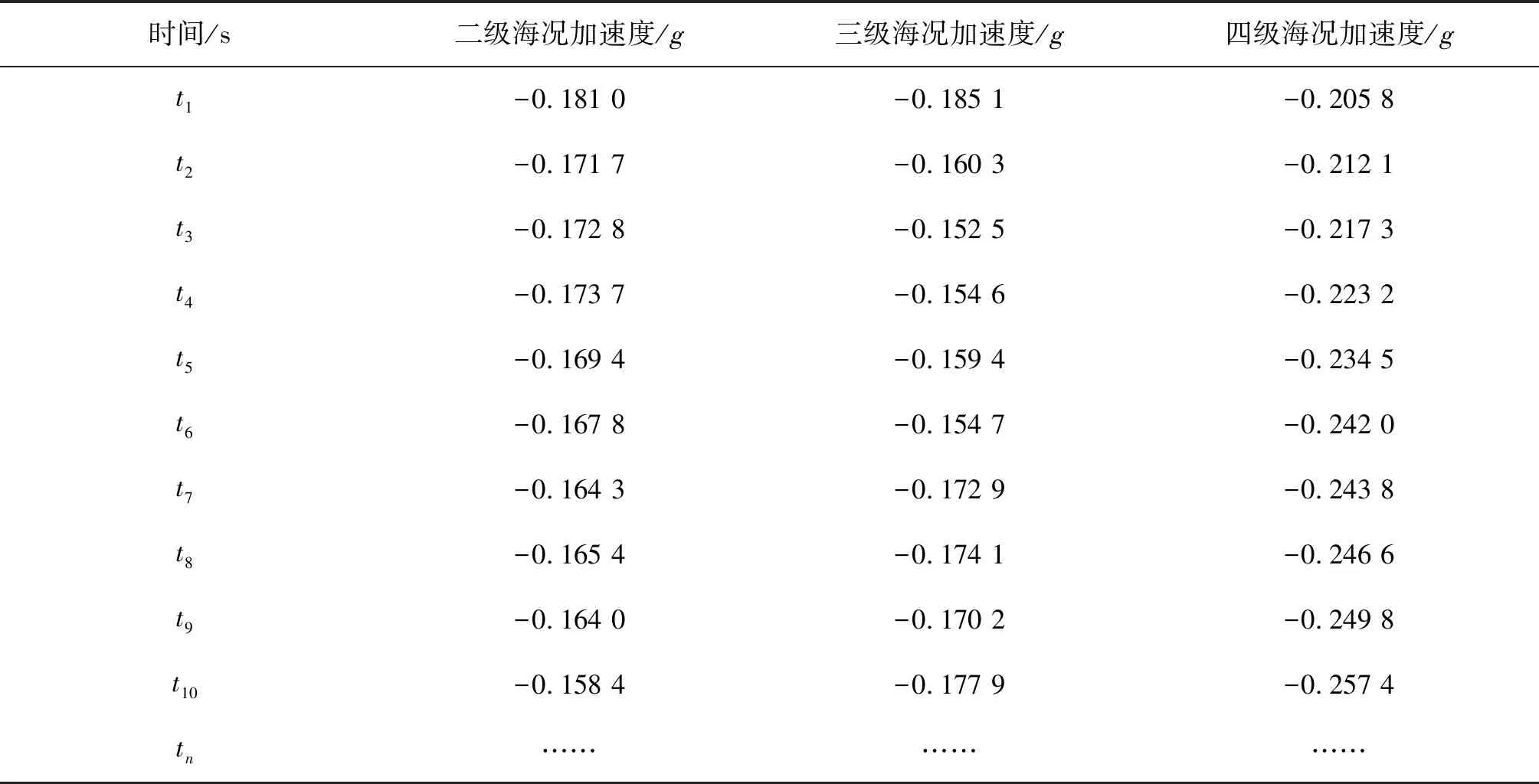
表1 船舶運動姿態觀測數據表(部分)Tab. 1 Ship motion attitude observation data table (partial)

1.2 卡爾曼濾波

采集信號時由于傳感器自身和外界環境的影響，加速度信號中包含大量白噪聲，因此需要設計濾波器對加速度信號進行降噪濾波處理。卡爾曼濾波器建模簡單，數據解算速度快[12]，只需通過前一個估計值及觀測數據估計當前的信號值，采用遞推方式實時更新觀測數據，就可以解算出新的卡爾曼濾波值，因此很適合用來處理船舶升沉運動加速度信號。

由于采集到的不同海況下升沉運動的加速度信號為離散信號，因此需要先建立離散卡爾曼濾波器[13-14]，其系統狀態方程和測量方程如式(1)所示。

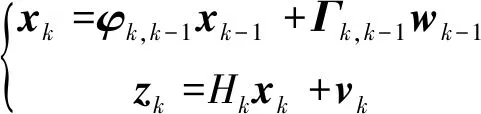
(1)

系統的最優預測誤差協方差矩陣Pk,k-1和最優增益矩陣Kk計算如式(2)所示。

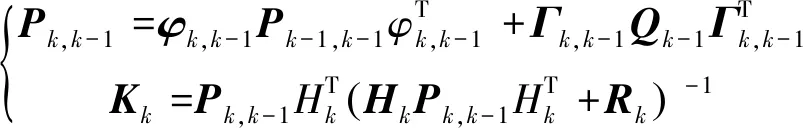
(2)

式中：φk,k-1為系統狀態轉移矩陣，xk-1為k-1時刻系統狀態量；Γk,k-1為噪聲系數矩陣，wk-1為系統噪聲；zk為k時刻系統測量值，Hk為系統測量矩陣，vk為測量噪聲；Qk-1,Rk分別為系統動態噪聲wk-1和觀測噪聲vk的方差陣。

利用公式(1)和(2)可以計算出k時刻系統狀態的最優濾波值，如式(3)所示。

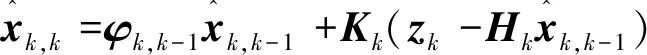
(3)

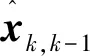
將二級海況、三級海況和四級海況下的三組升沉運動加速度信號輸入到設計好的卡爾曼濾波器中，得到濾波后的加速度信號曲線，如圖1、圖2和圖3所示。對比原始加速度信號和濾波后的加速度信號波形圖可知，設計的卡爾曼濾波器能較好的去除白噪聲，保留加速度信號的原有特征。

為了評估卡爾曼濾波器對升沉運動加速度信號的濾波效果，引入信噪比(SNR)以及相關系數(R)。其中，信噪比為信號中有效成分與噪聲成分功率之比，是描述兩種成分之間比例關系的參數；相關系數可以反映原始加速度信號和濾波后的加速度信號之間的相關程度，計算公式如下所示。

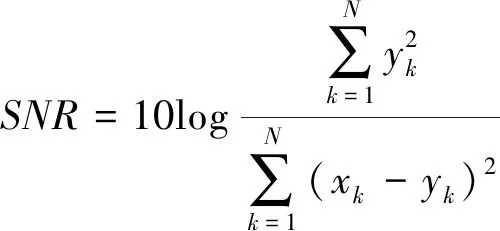
(4)

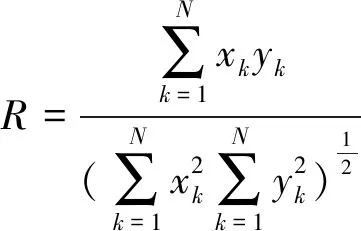
(5)

式中：xk為原始加速度信號，yk為濾波后的加速度信號。

表2 卡爾曼濾波器在不同海況下的SNR和R值Tab. 2 SNR and R values of Kalman filter under different sea states

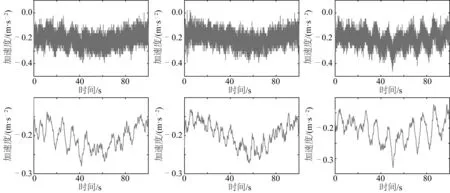
圖1 二級海況下加速度信號濾波前后對比Fig. 1 Comparison of the acceleration signal before and after filtering in the level-two sea state

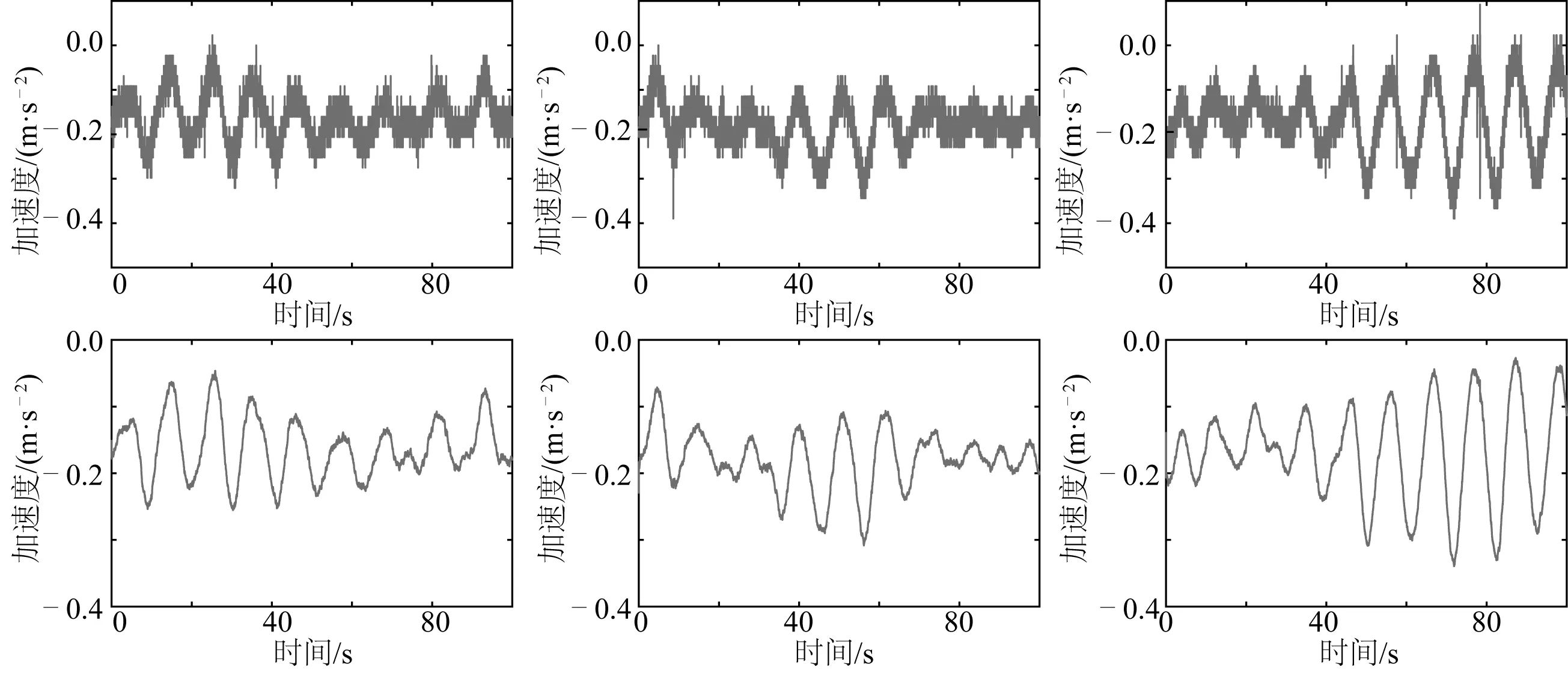
圖2 三級海況下加速度信號濾波前后對比Fig. 2 Comparison of the acceleration signal before and after filtering in the level-three sea state

圖3 四級海況下加速度信號濾波前后對比Fig. 3 Comparison of the acceleration signal before and after filtering in the level-four sea state

表2總結了卡爾曼濾波器在不同海況下的信噪比SNR和相關系數R，可知三級海況下卡爾曼濾波器的信噪比最低，平均值為42.630 4，二級海況下最高，平均可達到66.990 8。此外，原始加速度信號和濾波后的加速度信號的相關系數均在0.9以上，說明加速度信號使用卡爾曼濾波器具有很好的濾波效果。

1.3 加速度二次積分

波浪補償裝置主要控制船舶升沉運動的位移信號，因此需要將加速度信號轉換成位移信號。由于船舶升沉運動的加速度信號為低頻信號，采用兩次頻域積分會導致低頻信號誤差較大，影響積分后的位移信號精度[15]，又因為加速度信號中包含一定的誤差項，采用兩次時域積分會產生較大的累積誤差[16]。因此，使用時域-頻域積分，既避免了時域積分中二次趨勢項的產生，也降低了頻域積分對低頻信號精度造成的影響[17-18]。首先進行時域積分，離散加速度信號的時域積分方法主要有梯形積分和辛普森積分等，其中梯形公式由于計算簡單、精度高而被廣泛使用，其速度計算公式為

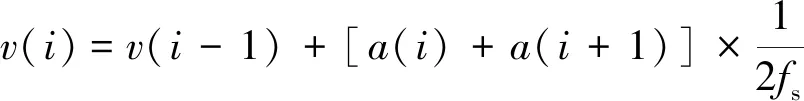
(6)

式中：v為積分后的速度值，a為加速度信號，fs為采樣頻率。

其次將得到的速度值v(i)進行傅里葉變換得到速度的頻域值V(k)，然后在頻域上積分，計算公式如式(7)、式(8)：

(7)

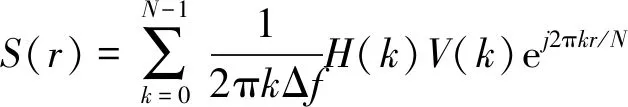
(8)

式中：S(r)為位移的頻域值，Δf為頻率分辨率。H(k)為頻域值帶通濾波器的帶寬，如式(9)所示，fd為下限截止頻率，fu為上限截止頻率。

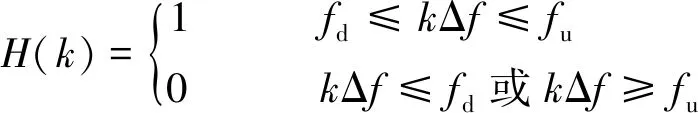
(9)

在頻域積分中，上、下限截止頻率會影響積分誤差的大小, 其確定方法主要有兩種：若加速度信號的頻帶已知，則將信號的頻帶上、下限頻率作為頻域積分的上限截止頻率和下限截止頻率；若加速度信號的頻帶未知，首先對加速度信號進行頻譜分析，將功率譜密度曲線中顯著低于其它頻帶的頻率點作為頻域積分的下限截止頻率，顯著高于其它頻帶的頻率點作為頻域積分的上限截止頻率。

根據時域-頻域積分法，在MATLAB軟件中設計加速度二次積分模塊，將濾波后的加速度信號積分為位移信號，圖4、圖5和圖6分別為二級海況、三級海況和四級海況下船舶升沉運動加速度和位移波形圖。由圖可知，隨著海況增大，升沉位移的幅值也越來越大，此外，低海況時船舶升沉位移曲線較平穩，高海況時變化較為劇烈。另外，采用頻域積分將時域積分中產生的趨勢項消除，使得積分后的位移曲線更加平滑。

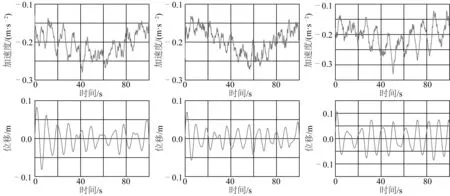
圖4 二級海況下加速度和位移波形Fig. 4 Acceleration and displacement wave forms in the level-two sea state

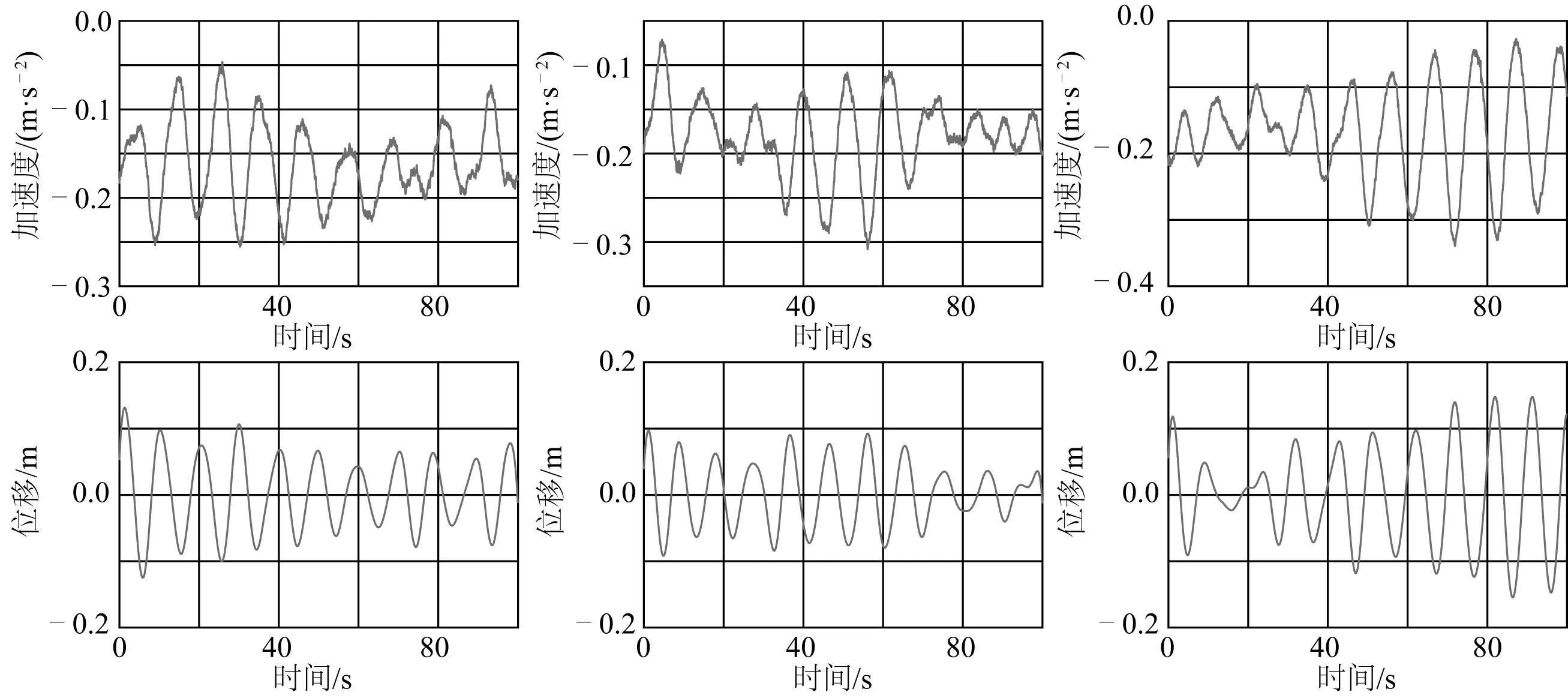
圖5 三級海況下加速度和位移波形Fig. 5 Acceleration and displacement wave forms in the level-three sea state

圖6 四級海況下加速度和位移波形Fig. 6 Acceleration and displacement wave forms in the level-four sea state

2 ARMA模型

ARMA模型的建立主要包括模型定階、參數估計和參數優化等過程[19]。設{xt}(t=1, 2, ……,N)為加速度二次積分得到的船舶升沉運動位移數據，船舶運動姿態位移xt不僅與其前k步的位移xt-1,xt-2, ……,xt-k有關，而且還和前l步的各項位移擾動yt-1,yt-2, ……,yt-k有關(k,l=1, 2, ……)，ARMA模型的數學表達式如式(10)所示：

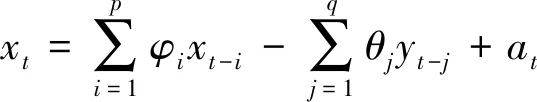
(10)

式中：p,q分別表示自回歸部分和滑動平均部分的階次；φi和θj分別為AR和MA部分的模型參數；at為測量誤差，通常為白噪聲序列。

2.1 ARMA模型定階

模型定階是為了尋找ARMA模型的最佳階數，本文通過采用AIC準則和BIC準則共同定階，以便在模型預測精度與模型計算復雜度之間尋找平衡。其中，AIC準則由日本學者Akaike H[20]于1974年首次提出，是一種衡量統計模型擬合優良性的標準。BIC準則由Schwarz[21]于1978年提出，通過加入模型復雜度懲罰因子來避免出現過擬合問題。

設{xt,t=1, 2, ……,N}為船舶升沉運動的位移數據，利用模型參數估計方法可以獲得在不同階數下的ARMA(p,q)模型，并計算出相應的AIC值和BIC值，如公式(11)所示：

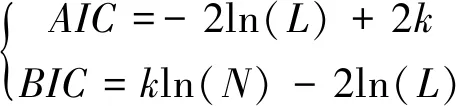
(11)

式中：k為模型參數個數，N為樣本數量；L為似然函數，計算公式如式(12)所示。懲罰項k·lnN在維數過大且訓練樣本數據較少時，可以有效避免維度災難問題。當AIC最小且BIC最小時，p和q為ARMA模型最佳的模型階數。

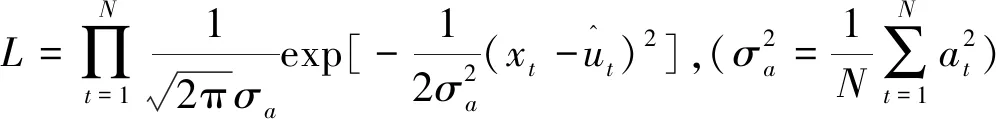
(12)

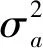
2.2 ARMA模型參數估計

長自回歸模型計算殘差法可以將ARMA 模型參數的非線性估計問題轉變為AR模型參數的線性估計問題，極大簡化計算過程，提高ARMA模型的預測效率[22-23]。本文采用該方法估計ARMA模型中的參數φi和θj，其基本原理為：同一升沉運動位移時序數據{xt}擬合成的AR(n) 模型和ARMA(p，q) 模型可以看成等價系統，兩種模型在同一時刻的殘差值at應相等。因此，可以將位移時序{xt}擬合出的AR(n) 模型的殘差at作為ARMA(p,q) 模型的at，再通過最小二乘法求解模型參數，其計算步驟如下所示。

首先將船舶升沉運動位移時序{xt}擬合出合適的AR(n)(n≥p+q)模型，得到模型參數φi(i=1, 2, ……,n)，然后計算殘差序列at。

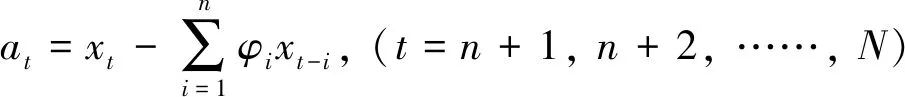
(13)

通過AR(n)模型可以得到從t=n+1至t=N的殘差序列{at}，將{at}代入ARMA(p，q)模型中，如矩陣方程(14)所示。

Y=Xβ+A

(14)

式中：Y為船舶升沉位移預測值矩陣；X為升沉位移測量值矩陣；β為ARMA模型參數矩陣；A為白噪聲序列；如公式(15)～(18)所示。

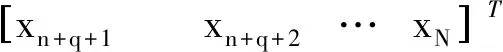
(15)

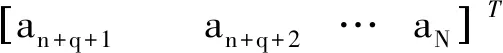
(16)

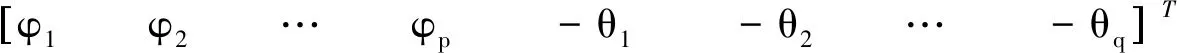
(17)

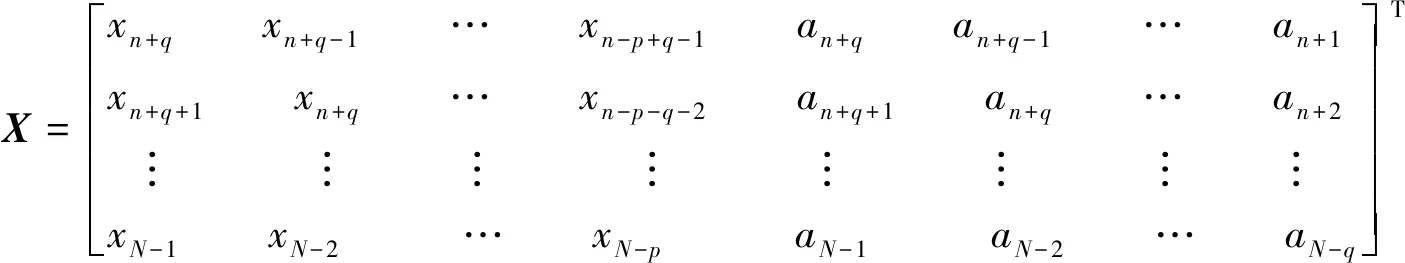
(18)

由于矩陣X中的參數均已知，可以使用最小二乘法估計模型參數β，見式(19)。

β=(XTX)-1XTY

(19)

長自回歸模型計算殘差法的參數估計流程如圖7所示。

圖7 長自回歸模型計算殘差法流程Fig. 7 Flow chart of long auto-regressive model calculation residual method

3 Newton-ARMA模型

3.1 ARMA模型參數優化目標函數

前述ARMA模型可以表示為公式(20)的形式：

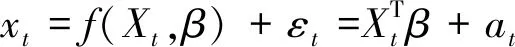
(20)

式中：Xt如公式(15)所示，由不同時刻船舶升沉運動加速度信號組成；β如公式(14)所示；at為模型的殘差。

為了選擇合適的模型參數β，通過建立目標函數S(β)，如公式(21)所示，將參數β的估計問題轉化為對S(β)的尋優問題，即保證模型的殘差平方和S(β)為極小，本文利用Newton法求解模型參數β。

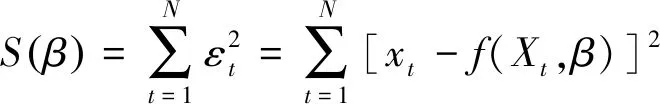
(21)

3.2 Newton法的迭代原理

首先在β(0)處對ARMA模型中的f(Xt,β)進行Taylor展開，并去掉二階以上的高階項，然后進行一系列線性最小二乘估計，直到迭代收斂到指定的范圍[10, 24]。將參數初值β(0)代入模型中得到殘差值，如公式(22)所示。

(22)

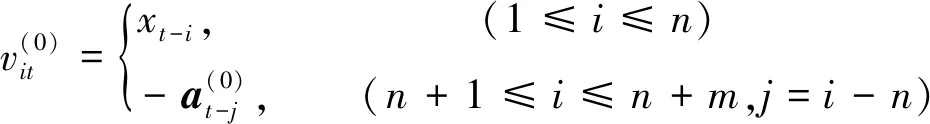
(23)

模型參數估計β與其初值β(0)之差可以通過公式(24)求得。

h(0)=[v(0)Tv(0)]-1v(0)Ta(0)

(24)

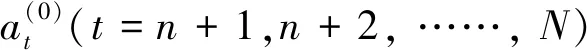
3.3 Newton法參數尋優過程

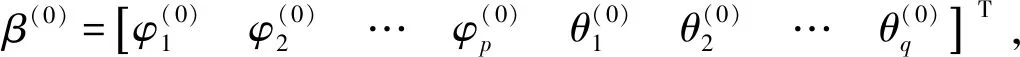
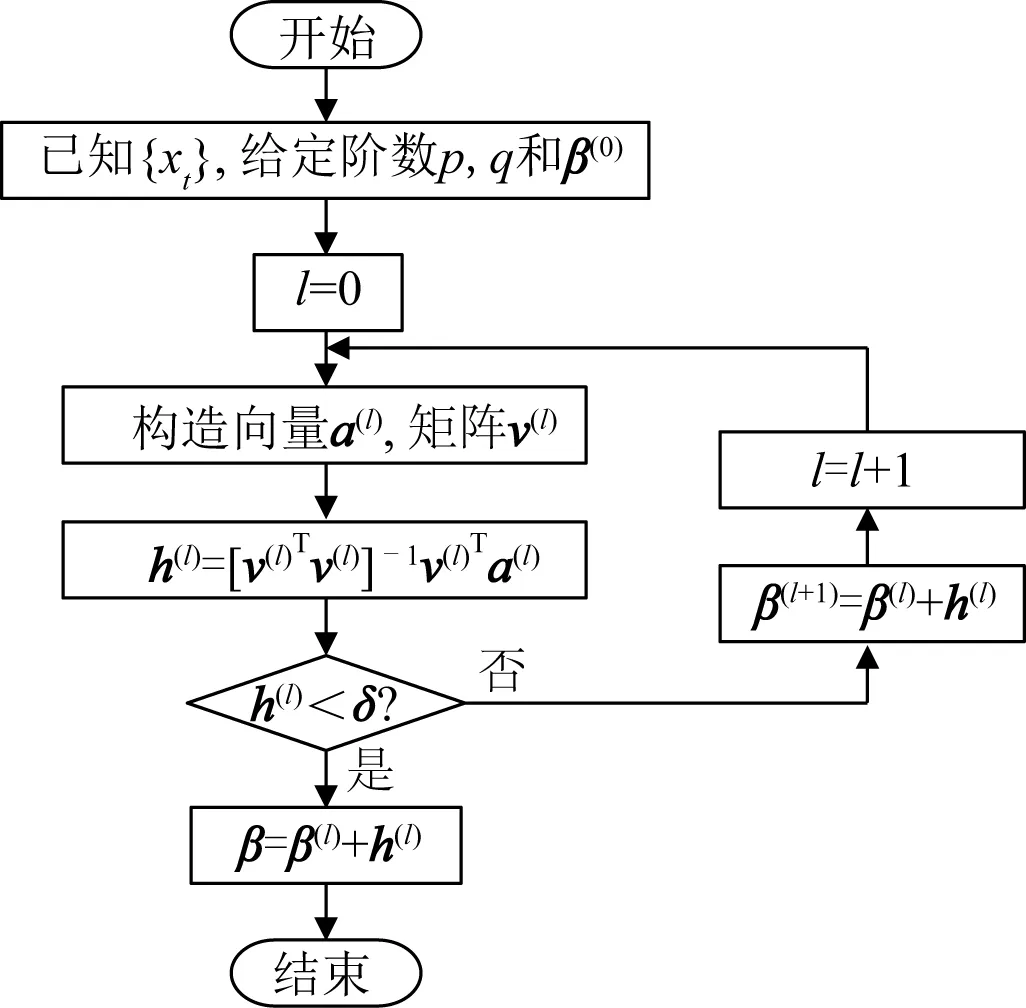
圖8 Newton法參數尋優流程Fig. 8 Flow chart of parameter optimization by Newton method

步驟2：設l為迭代循環變量，第一次迭代前設置l=0；

步驟4：按照公式(24)估計出h(l)；

步驟5：判斷h(l)是否小于預設的精度界限δ，即迭代結果是否收斂，如果h(l)<δ，則ARMA模型參數的估計值為β=β(l)+h(l)，如果h(l)≥δ，則進行下一步迭代運算；

步驟6：將β(l+1)=β(l)+h(l)作為下一次迭代計算的初值，令l=l+1轉入步驟3中繼續迭代，直到h(l)<δ迭代結束。Newton法參數尋優過程的流程如圖8所示。

4 仿真結果分析

仿真數據為加速度二次積分模塊得到的船舶升沉運動位移數據，建立Newton-ARMA模型首先進行模型定階，根據上述步驟1，令ARMA模型中自回歸部分的階數p從1到10，滑動平均部分的階數q從1到10，分別求出各階數的AIC和BIC值，找出不同階數下AIC和BIC的最小值，即為模型的最佳階數，如表3所示。

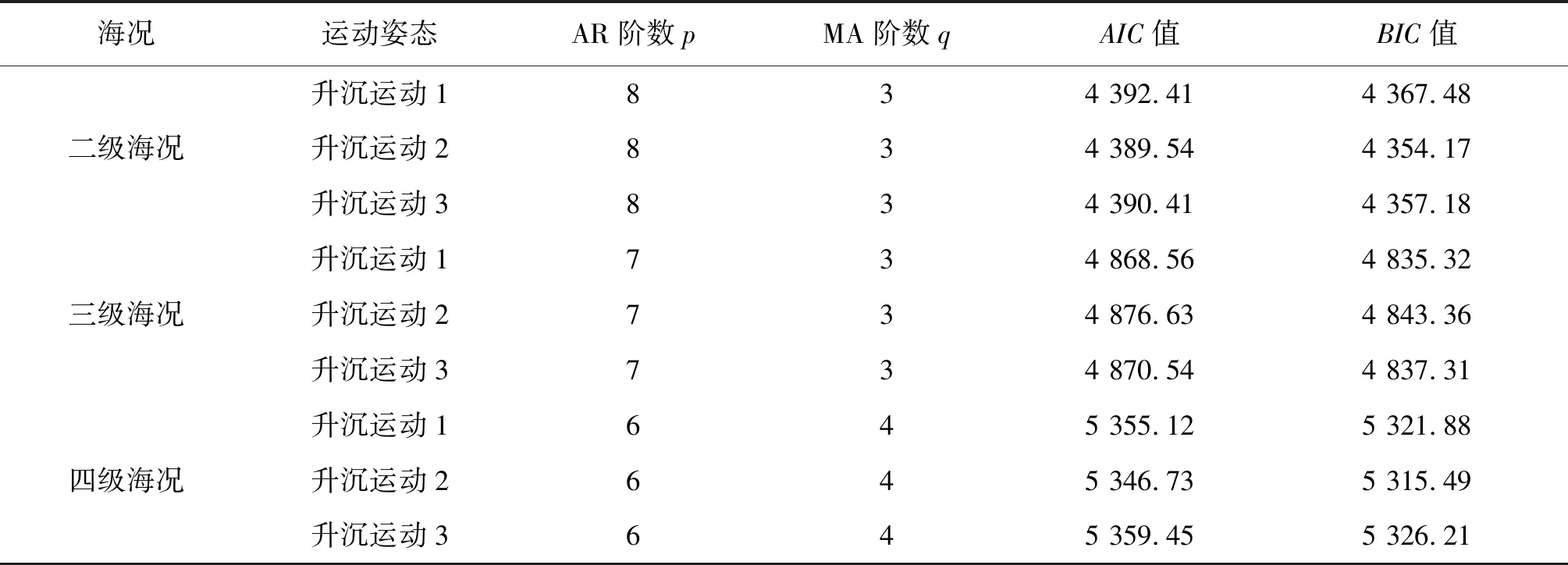
表3 不同階數下的AIC和BIC值Tab. 3 AIC and BIC values at different orders

由表3可知，二級海況下Newton-ARMA模型的最佳階數為p=8，q=3，三級海況下Newton-ARMA模型的最佳階數為p=7，q=3，四級海況下Newton-ARMA模型的最佳階數為p=6，q=3。根據最佳階數建立ARMA模型，利用長自回歸模型計算殘差法得到模型參數初值β(0)，并利用Newton法對β(0)進行迭代尋優，設置精度界限δ=10-5，運算完成后得到不同海況下升沉運動1、升沉運動2和升沉運動3的Newton-ARMA模型參數估計值β，如表4所示。

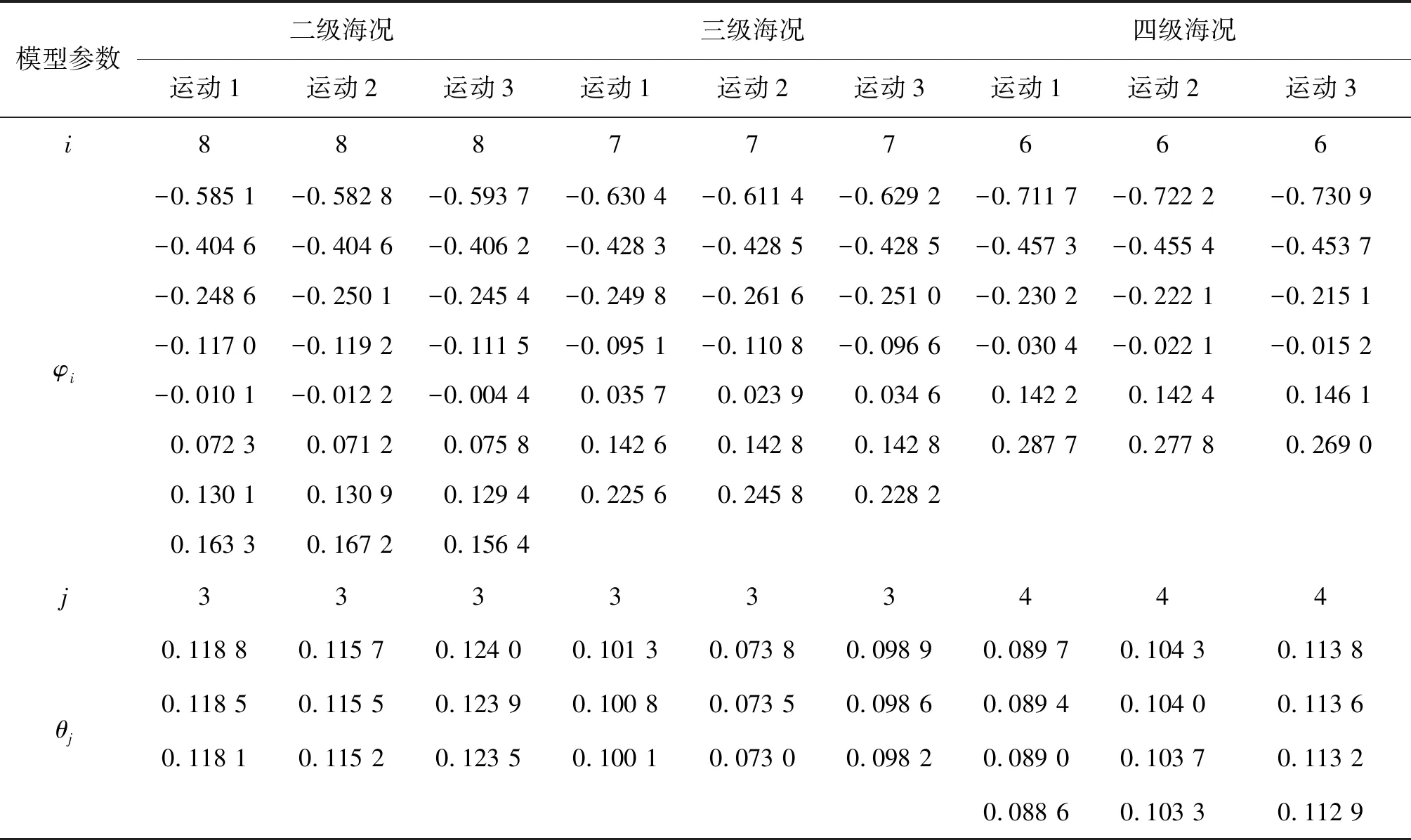
表4 不同海況下升沉運動的Newton-ARMA模型參數Tab. 4 Newton-ARMA model parameters for heave motion in different sea states

基于得到的三種海況下船舶升沉運動的Newton-ARMA模型，分別進行1 s到10 s的預測，預測結果如圖9、圖10和圖11所示。圖中實線(每段100 s，共9段)表示測量的船舶升沉運動位移信號曲線；實線(每段90 s，共9段)表示使用Newton-ARMA模型擬合出的船舶升沉運動位移曲線；虛線(每段10 s，共9段)表示使用Newton-ARMA模型預測10 s內船舶升沉運動位移曲線；點畫線(每段90 s，共9段)表示只使用ARMA模型擬合出的船舶升沉運動位移曲線；點線(每段10 s，共9段)表示只使用ARMA模型預測10 s內船舶升沉運動位移曲線。由圖可知，Newton-ARMA模型擬合出的船舶升沉運動位移曲線更貼近于測量數據的升沉位移曲線，說明使用Newton法優化ARMA模型參數使得預測模型可以更加真實地反映船舶實際的升沉運動狀態，通過對比Newton-ARMA模型和ARMA模型預測10 s內船舶升沉運動位移的曲線，能夠很好地證明該結論。

圖9 二級海況下船舶升沉運動預報曲線Fig. 9 Ship heave motion prediction curve in level-two sea state

圖10 三級海況下船舶升沉運動預報曲線Fig. 10 Ship heave motion prediction curve in level-three sea state

圖11 四級海況下船舶升沉運動預報曲線Fig. 11 Ship heave motion prediction curve in level-four sea state

根據建立的不同預測模型，可以分別求解出不同時長時預測值與測量值的均方根誤差RMSE，如圖12所示。由圖可知，隨著預測時間的增大均方誤差不斷增大，預測精度逐漸減小。以Newton-ARMA模型為例，在預測二級海況的升沉運動1中，當預測時間從1 s增加到10 s時，均方誤差值從0.004 3 m增加到0.032 8 m。此外，使用ARMA模型對二級海況、三級海況和四級海況升沉運動的平均預測精度分別為85.31%、82.46%以及80.21%，而使用Newton-ARMA模型的平均預測精度分別可達89.43%、88.53%以及87.78%，由此可知采用Newton法優化ARMA模型參數可以顯著提高船舶升沉運動的預測精度。

圖12 船舶運動預報均方根誤差Fig. 12 Ship motion prediction root mean square error

5 結 語

使用Newton法對ARMA模型參數進行優化，得到不同海況下船舶升沉運動的Newton-ARMA預測模型，仿真結果表明，Newton-ARMA模型對船舶升沉運動的預測時間可達10 s以上，有效地減小了波浪補償裝置控制系統的時延，且預測精度得到顯著提升，最高可達89.43%，由此表明Newton-ARMA模型對船舶升沉運動具有較好的預測效果。此外，建立Newton-ARMA模型首先采用AIC準則和BIC準則共同確定模型的階數，可以避免出現過擬合現象導致模型復雜的問題；利用長自回歸模型計算殘差法計算模型參數初值，可以將非線性估計問題轉化為線性估計問題，簡化了計算過程，使得尋優迭代速度更快。