基于拓撲優化與多目標優化的集裝箱相似畸變模型設計

劉佳琦，蔡忠華，王德禹

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240； 2. 高新船舶與深海開發裝備協同創新中心，上海 200240)

集裝箱運輸因其裝卸貨物效率高、運輸時間短和成本低等優點，在航運市場得到廣泛應用。目前，大約90%的非散裝貨物海運都是利用集裝箱來完成運輸[1]。隨著集裝箱的廣泛使用，集裝箱墜海事故發生率隨之升高。據估計，每年海上運輸過程中約有10 000個集裝箱丟失[2]，這對航運業造成了巨大的經濟損失。Aguiar[1]等認為對集裝箱堆垛進行動力學響應研究是探究集裝箱丟失機理的方法之一。而目前，該項研究大部分是建立在有限元軟件數值計算的基礎上，這不能完全反映堆棧系統的真實特性。而在海運過程中，因受到模型體積大，試驗難度大和成本高等多方面因素的限制[3]，難以對高達幾十米的集裝箱堆垛進行試驗測量。因此，在實驗室條件下，利用相似模型來模擬集裝箱，進而構建集裝箱堆垛系統，并對其進行試驗研究是可行的方法，不僅可以驗證有限元數值模擬的準確性，還能得到堆垛系統最真實的力學行為。

模型試驗研究方法是建立與原型相似的模型進行試驗研究，從而揭示原型本質和規律的方法[4]，其理論基礎是相似定理。在設計集裝箱相似模型時，由于集裝箱具有薄壁構件(厚度與結構件最小平面跨度之比在1/80和1/5之間的構件[5])，若采用完全幾何相似的縮尺模型進行試驗，會出現相似模型的厚度太小而無法加工的情況，并且在加工焊接時極易產生初始應力和初始變形，這些初始缺陷可能會成為影響其結構力學行為的一個重要因素。初始缺陷影響系數的不一致代表了初始條件的不一致，這一點與相似第三定理相違背[6]。同時，集裝箱原模型框架結構不是標準的型材制作，形狀并不規則。除了框架結構，其它部分主要是采用蒙皮式波紋板結構，這種結構在實驗室條件下很難制作。

鑒于集裝箱結構的特殊性，本文提出了一種快速構建集裝箱相似畸變模型的方法。首先，建立20英尺ISO貨運集裝箱有限元模型，基于有限元方法提取其靜力學和動力學特征參數；其次，基于Froude縮尺定理確定縮尺集裝箱特征參數目標值；然后，構建相似集裝箱的結構模型，利用拓撲優化對縮尺集裝箱墻壁結構的材料分布進行優化；最終，基于多目標優化算法對縮尺有限元模型的設計參數進行尋優直至尋優目標真值收斂至目標值，優化確定的縮尺有限元模型即為集裝箱相似模型。最后采用有限元分析驗證了該畸變相似模型的合理性。研究結果表明：本文的模型優化設計方法合理有效，設計的模型不僅滿足模型的加工工藝要求，還能預測集裝箱的力學行為。

1 20英尺ISO貨運集裝箱模型

標準20英尺ISO貨運集裝箱三維模型如圖1所示，它的主要尺寸和材料參數信息[7]如表1所示。采用Patran有限元軟件構建集裝箱的有限元模型，模型的單元尺寸、形狀和類型等詳細信息見表2。縮尺模型與全尺寸模型在所有相似參數上完全相似是很難實現的。選擇重要參數而忽略次要參數，雖然會導致畸變模型和原型之間產生誤差[8]，但誤差的大小取決于選擇參數對模型的影響程度。因此，選擇對集裝箱的機械性能影響較大的參數，包括：模型質量，慣性矩，結構剛度，第一階模態頻率，第一階模態振型等作為重要參數。為了便于貨物裝卸，20英尺ISO貨運集裝箱采用了一端封閉，另一端雙開門的結構形式，如圖2所示。這導致開口端(開門端)和閉口端(封閉端)的橫向剛度存在較大差異，需要分別考慮。

利用有限元分析獲得20英尺ISO貨運集裝箱的主要特征參數，計算結果與Aguiar[1]等人保持一致，如表3所示。其中，集裝箱的試驗方法和要求如表4所示。

圖1 20英尺集裝箱結構示意Fig. 1 20-ft container structure diagram

圖2 20英尺ISO貨運集裝箱Fig. 2 20-ft ISO freight container

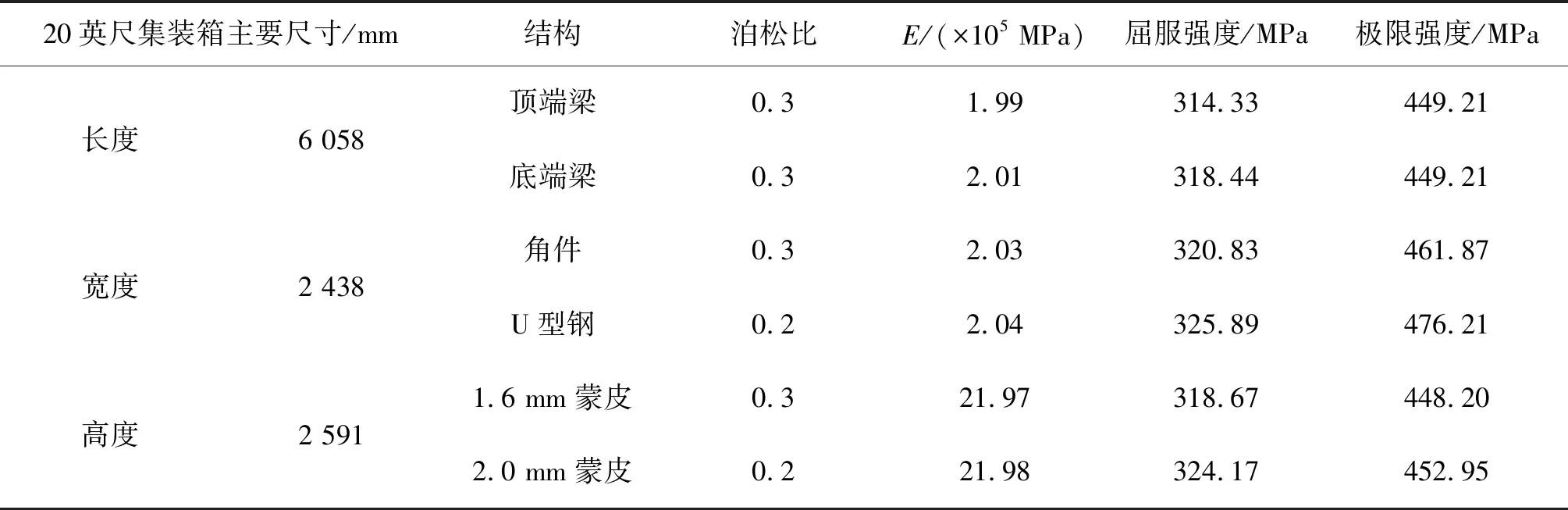
表1 20英尺集裝箱的主要尺寸和材料參數Tab. 1 Main size and material parameters of 20-ft container model

表2 20英尺集裝箱有限元模型構造細節Tab. 2 Construction details of 20-ft container finite element model

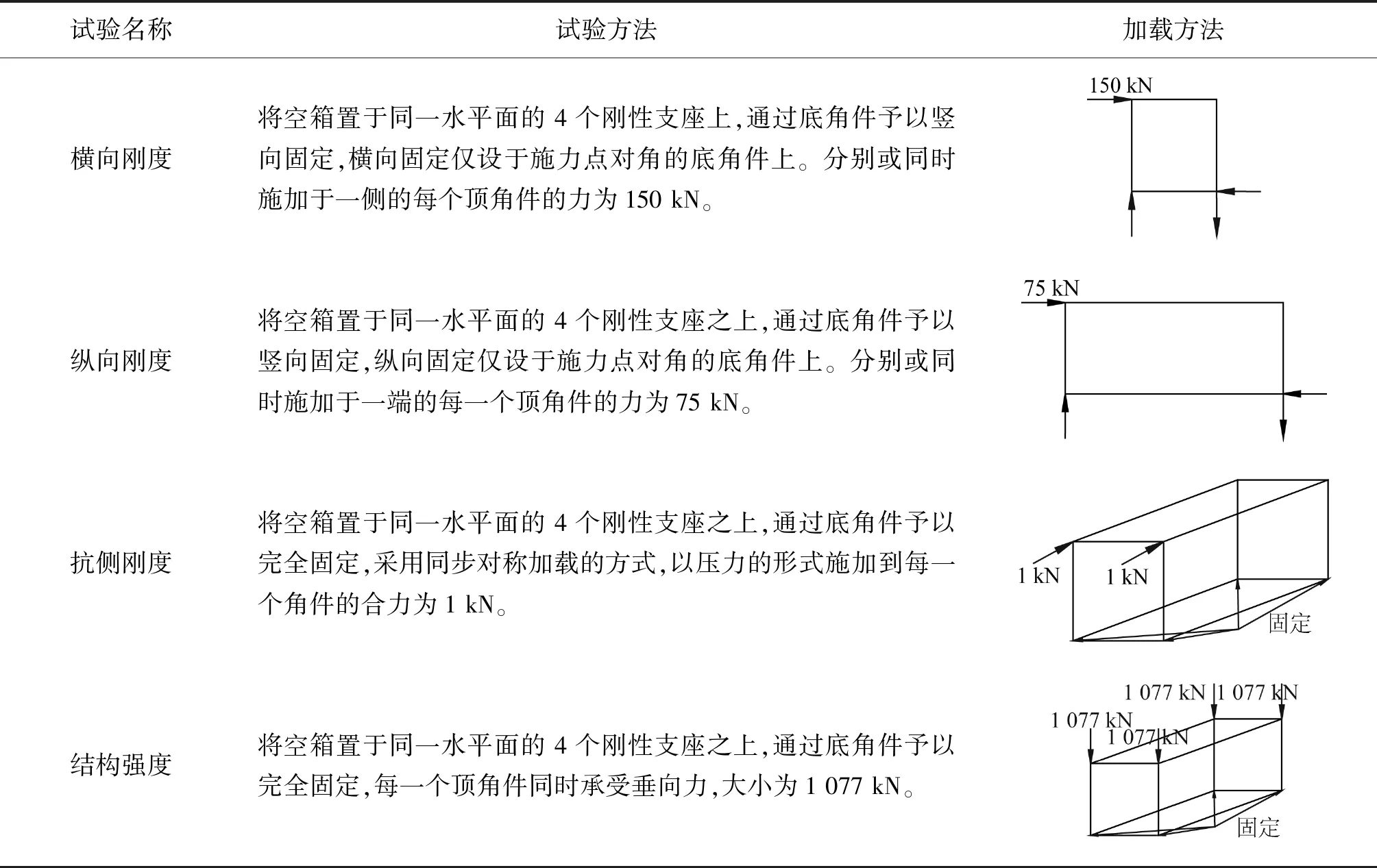
表4 集裝箱試驗方法與要求[9-10] Tab. 4 Methods and requirements of container test[9-10]

2 20英尺ISO貨運集裝箱縮尺模型設計

2.1 相似設計準則

幾何相似是指兩個系統中相對應的幾何要素的比值是一個常數。運動相似是指兩個系統中對應的運動參數在時間上的相似性，比如速度、加速度等。幾何相似和運動相似可以通過Froude縮尺準則來實現。動力學相似指作用于系統的力之間的比率是固定值。依據重力與慣性力之比，彈性力與慣性力之比兩個無量綱數，來確定縮尺模型的物理(尺寸、質量)和結構(縱向、橫向剛度)信息，使得縮尺集裝箱與全尺寸集裝箱在幾何、運動、動力學方面的對應相似。其中，Froude 縮尺準則[11]信息如表5所示，其中，λ為縮尺比。

表5 Froude縮尺準則Tab. 5 Froude scaling law

2.2 縮尺模型的構造

大比尺模型雖然可以與實際的結構形式上更為相似，但是制作的成本更高，對試驗環境的要求也越高，模型的裝卸、測試都會有一定的困難。小比尺相似模型則因尺寸過小，不利于加工制造，且尺寸越小，因焊接產生的殘余應力與初始變形對試驗結果的影響會越大，導致試驗結果的不準確。因此模型設計一方面應盡量做到與實際結構在各方面保持相似，另一方面還需要考慮模型制作的便利性和實驗平臺的限制等。本文為節約模型制作成本，降低對試驗環境要求，取模型的縮小比例為1∶10，即λ=10。

相似模型的設計思路如圖3所示。首先，基于有限元方法，建立20英尺標準海運干貨集裝箱結構1∶1的有限元模型，并提取其靜力學和動力學特征參數目標值；然后，基于Froude定理確定縮尺集裝箱靜力學和動力學特征參數目標值；其次，在考慮加工制造限制的前提下，選定縮尺集裝箱各結構構件的截面形式與尺寸，構建縮尺集裝箱結構模型，利用拓撲優化對縮尺集裝箱墻壁結構的材料分布進行優化，確定縮尺集裝箱的墻壁結構形狀。基于拓撲優化得到的集裝箱結構形式，利用多目標優化算法對縮尺有限元模型的設計參數進行尋優，若目標真值無法收斂，則更改集裝箱的各結構構件的截面形式或尺寸，重新進行拓撲優化與多目標優化，直至尋優目標真值收斂至目標值，優化確定的縮尺有限元模型即為集裝箱相似模型。

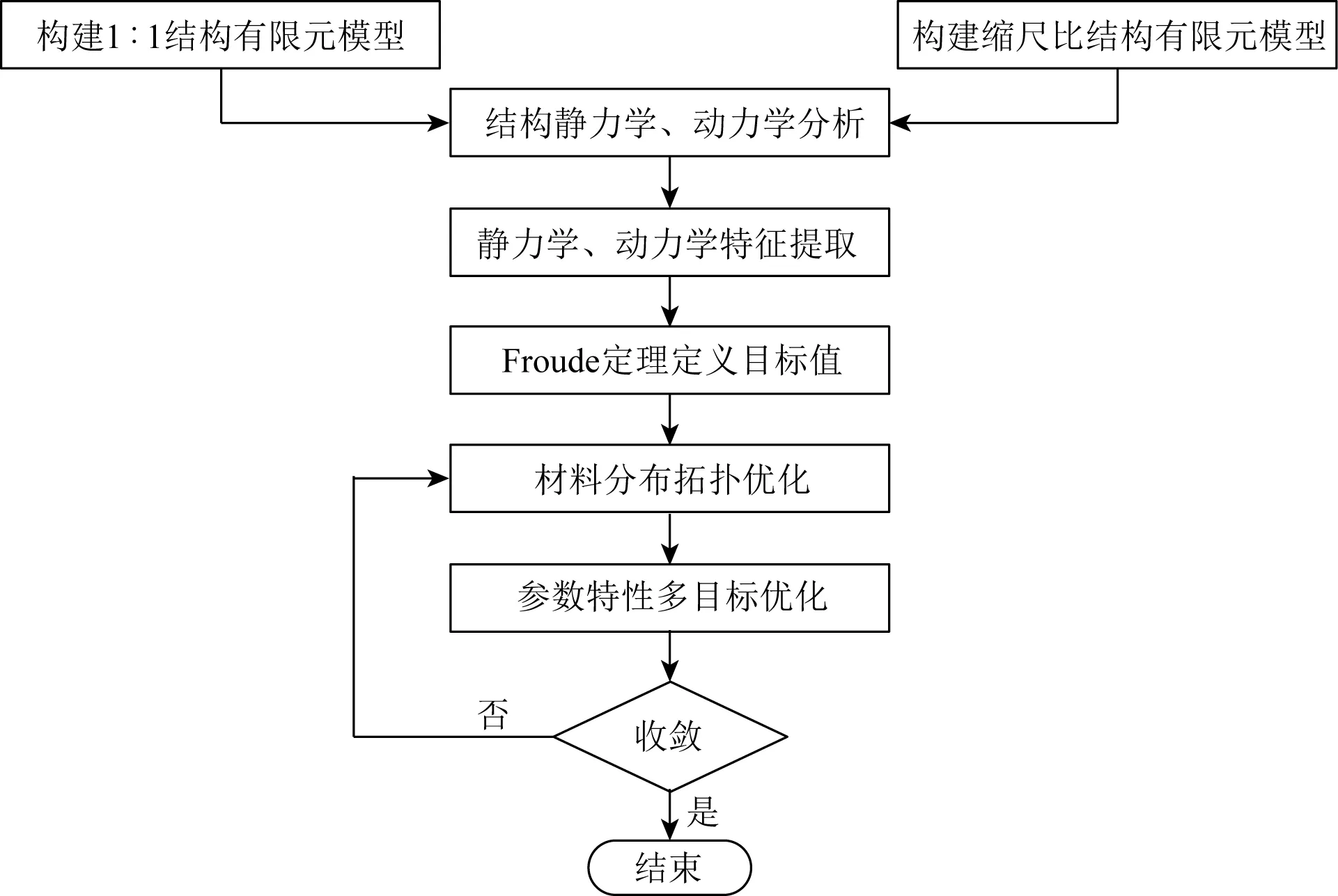
圖3 相似模型設計思路Fig. 3 Design way of similarity model

2.2.1 拓撲優化

為解決實驗室條件下無法加工蒙皮波紋板結構的問題，利用平板進行替代。因加工水平的限制，在平板選擇最小厚度，模型質量仍遠遠超過目標值。因此，需要利用拓撲優化對縮尺集裝箱的墻壁結構的材料分布進行優化，在保證結構的特征性能前提下，最大程度地減輕模型的重量。載荷條件與約束條件對拓撲優化結果十分重要，因此，需要考慮在實際情況下集裝箱的受力情況。

圖4 載荷與約束條件Fig. 4 Load and constraints condition

20英尺ISO貨運集裝箱在實際使用期間，集裝箱底部的4個角鑄件通過扭鎖固定在艙蓋板或者下層的集裝箱頂部，集裝箱頂部的4個角承受著上層集裝箱的重量和相鄰的集裝箱堆垛在集裝箱長邊方向和短邊方向力的作用。因此約束條件為底部箱角完全固定，載荷條件為頂部的4個角分別受到沿集裝箱長邊、短邊的集中力和垂直方向的壓力作用，每個角在X，Y，Z三個方向上的力分別為75、1 077和150 N[9]，具體的設置方式見圖4。雖然在規范中，不同方向剛度試驗底角件的固定方式存在差異，并非均為完全固定，但兩者計算結果差異很小，在工程上可以忽略。

基于ABAQUS的SIMP拓撲優化方法，建立了以墻壁結構單元密度為設計變量，畸變能密度最小(剛度最大化)為目標函數，優化前后體積分數百分比和位移約束為約束函數的拓撲優化數學模型，對墻壁結構的材料分布進行優化。其中，對集裝箱頂端箱角的四個點進行位移約束，以保證集裝箱的箱角不會產生大變形。拓撲優化的數學模型為：

式中：F(ηi)表示結構的畸變能密度，ηi表示第i個單元的偽密度，α表示體積減小的百分比，V0表示為墻壁結構初始體積，D0表示節點的許用位移偏移值。

本文利用ABAQUS軟件中變密度法對不同體積減小百分比和節點許用位移進行計算，隨著體積減小分數與許用位移的不斷減小，優化獲得的墻壁結構趨于穩定(一致)。當選擇α=5%，D0=0.02時，優化后的結構形式如圖5所示。考慮到現實中加工制造的條件，對拓撲優化的結果進行修正，如圖6所示。對修正后的集裝箱模型進行靜力學分析，得到結果與原始模型進行對比，見表6。

表6 模型優化結果對比Tab. 6 Comparison of model results

圖5 拓撲優化結果Fig. 5 Results of topology optimization

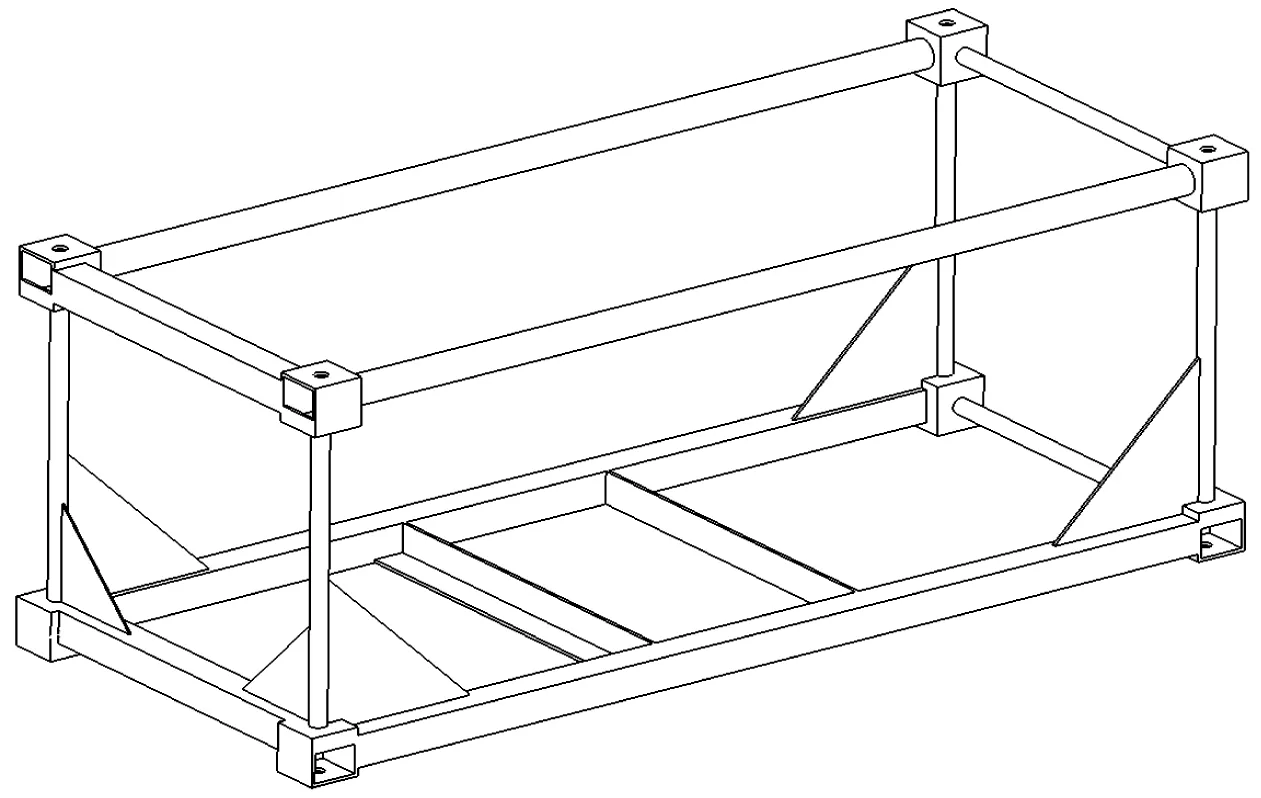
圖6 20英尺縮尺集裝箱幾何圖Fig. 6 Geometry diagram of 20-ft container

由分析結果可知，橫向剛度(開口端)和縱向剛度均增加，橫向剛度(閉口端)有所減小，優化區域的墻壁重量減小幅度達到91.6%。這表明，在集裝箱底端加上小肘板可以很好地給予結構支撐。基于由拓撲優化確定的集裝箱結構形式，進行多目標優化，以確定各個結構構件的厚度。

2.2.2 多目標優化

集裝箱畸變相似模型的構建是一個多學科、多目標和多約束的優化問題。優化目標包括結構質量、集裝箱的橫向剛度(開口端和閉口端)、縱向剛度、抗側剛度(開口端和閉口端)、一階模態頻率及振型。其中，采用靜力學分析計算結構剛度，加載方式與邊界條件信息詳見表4。利用模態分析計算模態頻率，并通過輸出一些典型點(集裝箱的8個箱角頂點)的位移來描繪振型，通過比較位移數值大小，初步判斷縮尺模型與原尺寸模型在振型是否一致。最終，對縮尺模型進行模態分析，驗證全尺寸模型與縮尺模型振型是否保持一致，以確保結果正確。約束條件包括結構強度和結構的可制造性等。結構強度的加載方式見表4。制造可行性表明該多目標分析的設計參數為離散型。本文采用逆向思維的設計方法，通過調整集裝箱模型各結構構件的特征參數來滿足設計目標。

運用多目標優化方法中的平方加權法將多目標優化問題轉化為單目標優化問題，通過調節權重因子，來解決各目標之間的量綱不一致性問題。每個目標的權重因子為該目標值的倒數。采用多島遺傳算法對目標函數尋優求解。作為在傳統遺傳算法基礎上建立的一種基于群體分組的并行性遺傳算法[12], 算法將每個進化種群劃分為若干個子種群，這些子種群被稱為“島嶼”。在每個島嶼上對子種群獨立地進行傳統遺傳算法操作，如選擇、交叉、變異等，每個島選定的個體定期轉移到另一島上，然后繼續進行傳統遺傳算法操作，從而有效地抑制早熟現象，有利于找到全局最優解[13]。多島遺傳算法的優化模型流程見圖7。

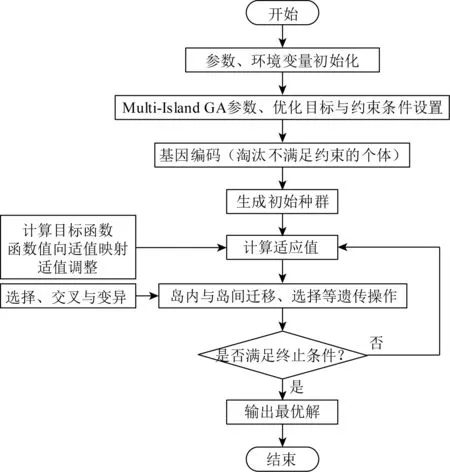
圖7 多島遺傳算法流程Fig. 7 Flow diagram of multi-island GA algorithm

對集裝箱縮尺模型進行模型修正。優化后的各個結構尺寸信息見表7。優化過程中變量變化曲線如圖8和圖9所示。

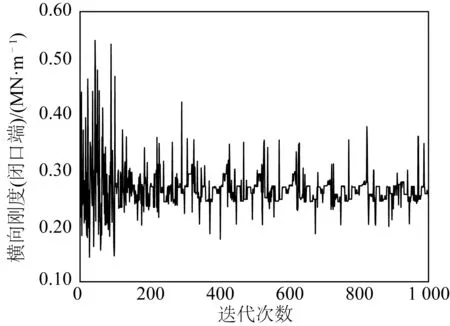
圖8 優化過程中結構橫向剛度曲線Fig. 8 Transverse stiffness curve in the optimization process

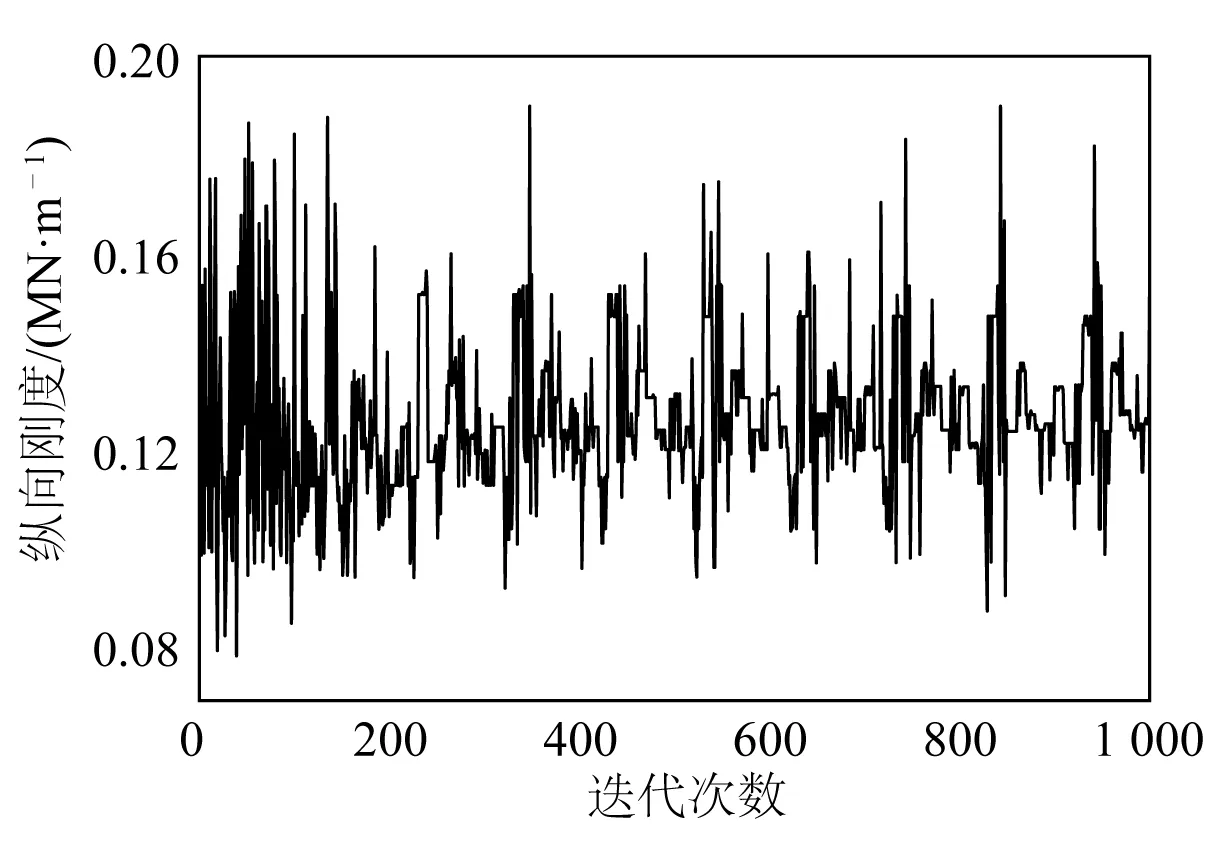
圖9 優化過程中縱向剛度曲線Fig. 9 Longitudinal stiffness curve in the optimization process

應用Froude縮尺準則來獲得縮尺模型的目標特征參數，選擇的設計變量及名稱見表7。通過建立數學模型來實現模型優化設計。可由下面的數學關系表示：

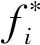
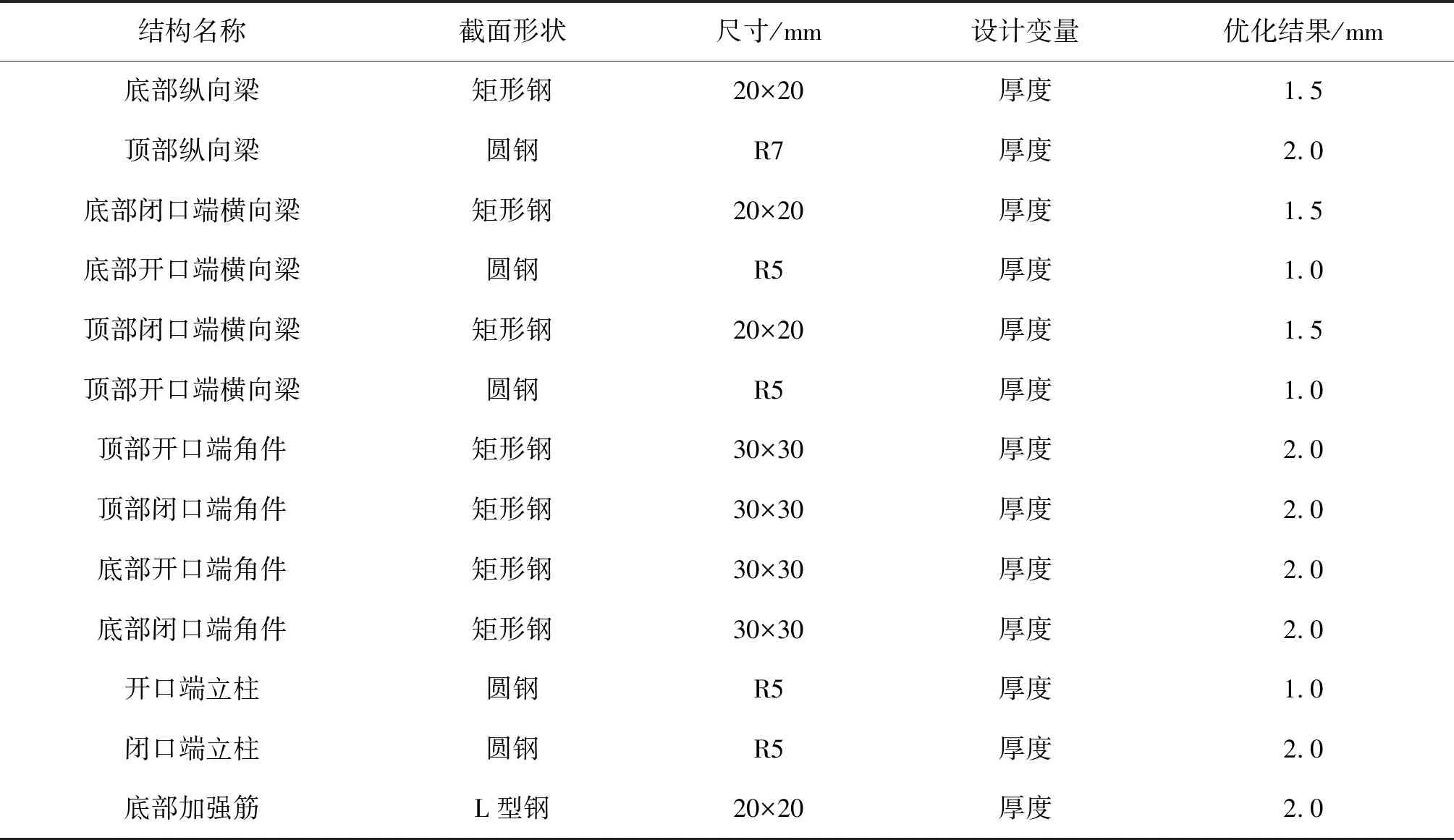
表7 縮尺模型幾何信息特征Tab. 7 Scale model geometric information feature

3 20英尺ISO貨運集裝箱縮尺模型驗證

縮尺集裝箱模型材料采用普通碳素鋼，其楊氏模量E=210 GPa，泊松比υ=0.3，密度為7 850 kg/m3。為了確定本文設計的縮尺集裝箱模型的可靠性，采用有限元方法來對其進行驗證。首先，對結構進行靜力學強度分析，來提取模型的結構剛度。然后，對結構進行模態分析來確定模型的頻率和模態特征。

3.1 靜力學強度分析

對縮尺集裝箱模型進行靜力學強度分析的加載方式與邊界條件，是參考CCS的《集裝箱檢驗規范》[9]的內容設置的，詳細信息見表4，利用有限元分析獲得的剛度計算結果如圖10所示。

圖10 縮尺集裝箱剛度有限元計算結果Fig. 10 Finite element analysis results of stiffness of the scaled model

3.2 模態分析

對縮尺集裝箱模型進行模態分析獲得的結果如表8所示，一階模態振型見圖11。通過與原尺寸集裝箱的一階模態振型圖對比，兩者一階模態振型一致，如圖12所示。因此，縮尺集裝箱的特征特性與由Froude縮尺準則獲得的目標值保持一致，驗證了經過多目標優化得到的集裝箱縮尺模型的準確性與有效性。縮尺集裝箱模型的詳細參數信息見表9。

表8 前3階集裝箱模型模態頻率 Hz Tab. 8 Former 3-order eigen frequencies of container model Hz

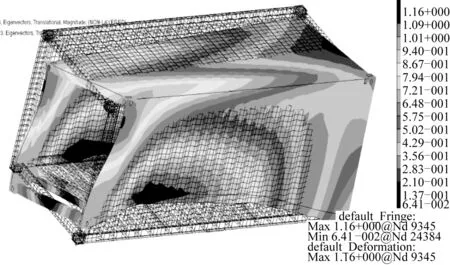
圖12 全尺寸集裝箱一階模態Fig. 12 1st-order natural frequency

由表8可知，最終構建的相似模型與原型結構的之間的靜力學行為差距較小，即本文所提出的方法可以有效減小原型結構和相似試驗模型之間的差值，使計算結果滿足預設目標的要求；從模態分析結果中可以看出，該集裝箱相似模型與目標結果差距較小，滿足目標要求，也驗證了所提方法的可行性和實用性。

表9 縮尺集裝箱模型參數信息表Tab. 9 Feature parameters of scaled model (λ=10)

4 結 語

基于Froude縮尺定理，結合拓撲優化與多目標優化，提出了一種構建相似畸變模型的方法。利用拓撲優化對縮尺集裝箱墻壁結構的材料分布進行優化，利用多目標優化來尋求滿足靜力學目標、動力學目標和結構的物理特性時各個結構的設計參數值。并對具有薄壁結構的ISO海運集裝箱進行相似畸變模型的構建。最終利用有限元分析驗證了該相似畸變模型的合理性。結果表明：設計的模型不僅滿足模型的加工工藝要求，還具有預測集裝箱力學行為的能力。該設計方法也具有一定的通用性，能為其它類型結構相似模型的構建提供新的思路。