焊接所致力學性能不均勻性對卷管法安裝管道完整性影響

李 英，李婧一

(天津大學 建筑工程學院 水利工程仿真與安全國家重點實驗室，天津 300350)

卷管鋪設有兩種形式：水平式與豎直式。卷管法中，管道先在陸地上進行預制接長，然后通過卷筒進行上卷退卷。卷管法可以實現20英寸直徑以下管道的高效安裝，因此被廣泛應用于深水油氣管道安裝。

卷管安裝過程中，管道受力過程十分復雜，會發生數次循環往復的彎曲，塑性變形將對管道結構性能和環縫焊接處的疲勞壽命產生影響。因此，研究人員對卷管鋪管中管道的材料性能、載荷效應、應變、橢圓度和局部屈曲等問題進行了研究。Hauch和Bai[1]研究了金屬管道的抗彎能力，給出了在壓力、縱向力和彎曲的組合載荷下管道極限承載能力的解析解，導出的方程可用于具有各向同性以及各向異性的高強度管道材料。Corana等[2]研究了軸向彎曲下薄壁管道屈曲的形成過程，并基于瞬時變形理論對管道局部屈曲進行預測，研究了管道材料特性的變化。基于非線性隨動強化材料，Chatzopoulou等[3]通過開展有限元分析，研究了卷管過程中循環彎曲載荷對厚壁無縫管道力學性能的影響，結果表明在卷管完成后管道材料性能表現為各向異性，且橫截面變形將導致管道力學抵抗性能降低。Mirzaee和Bastola[4]通過有限元方法模擬大塑性變形條件下管道殘余應力的分布，對卷管安裝中管道殘余焊接應力的分布進行預測。Karamanos 和Tassoulas[5]研究表明鋪管期間，管道下垂段受到高外壓時會發生顯著彎曲，將加劇管道橫截面橢圓化，導致管道坍塌。Karjadi等[6]對不同管徑和壁厚的管道進行了一系列彎曲試驗和有限元分析，獲得卷管期間管道的殘余橢圓度并進行管道局部屈曲校核。白勇等[7]通過與J-lay法的類比，簡化了卷管鋪管水下段的穩定性問題，并基于懸鏈線和小變形梁理論給出了應用卷管鋪管法鋪設柔性管的數值計算方法。為校直卷管鋪設中管道的塑性彎曲變形，王立權等[8]建立了一種基于彈塑性理論的校直模型，研究了管道材料參數和幾何參數對校直曲率的影響程度。張九菊等[9]基于應變能法和Ritz 法對海管橢圓度進行理論推導求解，并得到了橢圓度隨海管幾何參數變化的規律。

在管道生產過程中，通常需要對管材進行熱焊、熱軋，導致管道形成焊縫缺陷，同時管道性能將產生變化。此前已有針對焊縫缺陷對卷管鋪管影響的研究，Wastberg等[10]研究了卷管安裝過程中焊縫缺陷對管道性能的影響。李清泉和楊和振[11]對卷管鋪管過程進行有限元模擬并進行多軸疲勞分析，探討了未焊透和未融合兩種焊縫缺陷對管道材料特性的影響。另外，焊縫的裂紋可使管道產生應力集中，使管道在卷管鋪設過程中承受彎曲載荷的能力大幅降低，張九菊等[12]研究了具有不同裂紋角的管道在彎曲載荷下的變形并對結果數據進行函數擬合，得到了有裂紋海管的極限彎曲載荷表達式。

管道在環形焊縫處及其鄰域的熱影響區管段存在力學性能不均勻性，且由于管道在卷管安裝期間受到復雜的聯合載荷，因此在卷管安裝管道設計中應該充分研究焊接引起的不均勻性對于管道完整性的影響。首先將對卷管鋪管設計中數值模擬選用的材料模型進行探討，并以此為基礎針對焊接所致管道力學性能不均勻性的缺陷對卷管安裝中管道性能的影響進行研究。

1 管道材料本構模型

在進行管道非彈性力學行為的數值模擬時，一般采用各向同性硬化模型模擬管道的材料特性，但管道在承受循環彎曲載荷后，其材料性能將由各向同性變為各向異性，因此應選取合理的數值分析材料模型以獲得管道在卷管過程中的真實力學響應。為此分別使用各向同性硬化材料模型及非線性材料模型(選取Ramberg-Osgood材料模型)進行卷管鋪管仿真模擬，通過對比二者的有限元分析結果，選取適宜卷管安裝設計的數值分析材料模型作為研究管道力學性能不均勻性影響的基礎。

Ramberg-Osgood材料模型的應力-應變關系為：

圖1 應力-應變關系Fig. 1 Stress-strain relationship

式中：ε為應變；σ為應力；E為材料彈性模量；σy為材料屈服應力；α和β為材料常數，對于X65鋼，α=1.29，β=25.58。

各向同性硬化模型與Ramberg-Osgood材料模型的應力-應變關系如圖1所示。圖1表明在初始單調加載過程中兩種材料模型均與真實實驗結果吻合較好。而進入到反向加載階段后，各向同性材料模型仍通過單調加載所得到的力學響應為材料提供應力-應變關系，導致其值大于材料在滯后響應作用下的真實值。

2 有限元仿真模擬

2.1 有限元模型建立

采用ABAQUS建立非線性三維有限元模型模擬管道上卷及退卷的過程。管道及卷筒結構如圖2所示，管道外徑D=0.323 9 m，壁厚t=0.019 05 m，卷筒半徑R=8.5 m。管道總長s=160 D。為模擬焊接所致的管道力學性能不均勻性并探討其影響趨勢，假定焊接缺陷管段材料屈服應力低于規定屈服強度下限。取長為4D的CD管段定義為焊接缺陷管段，令該管段處材料的屈服應力為X65鋼的90%；其余管段為普通管段，管道材料采用X65鋼，材料屬性見表1和表2。

表1 材料屬性Tab. 1 Material properties

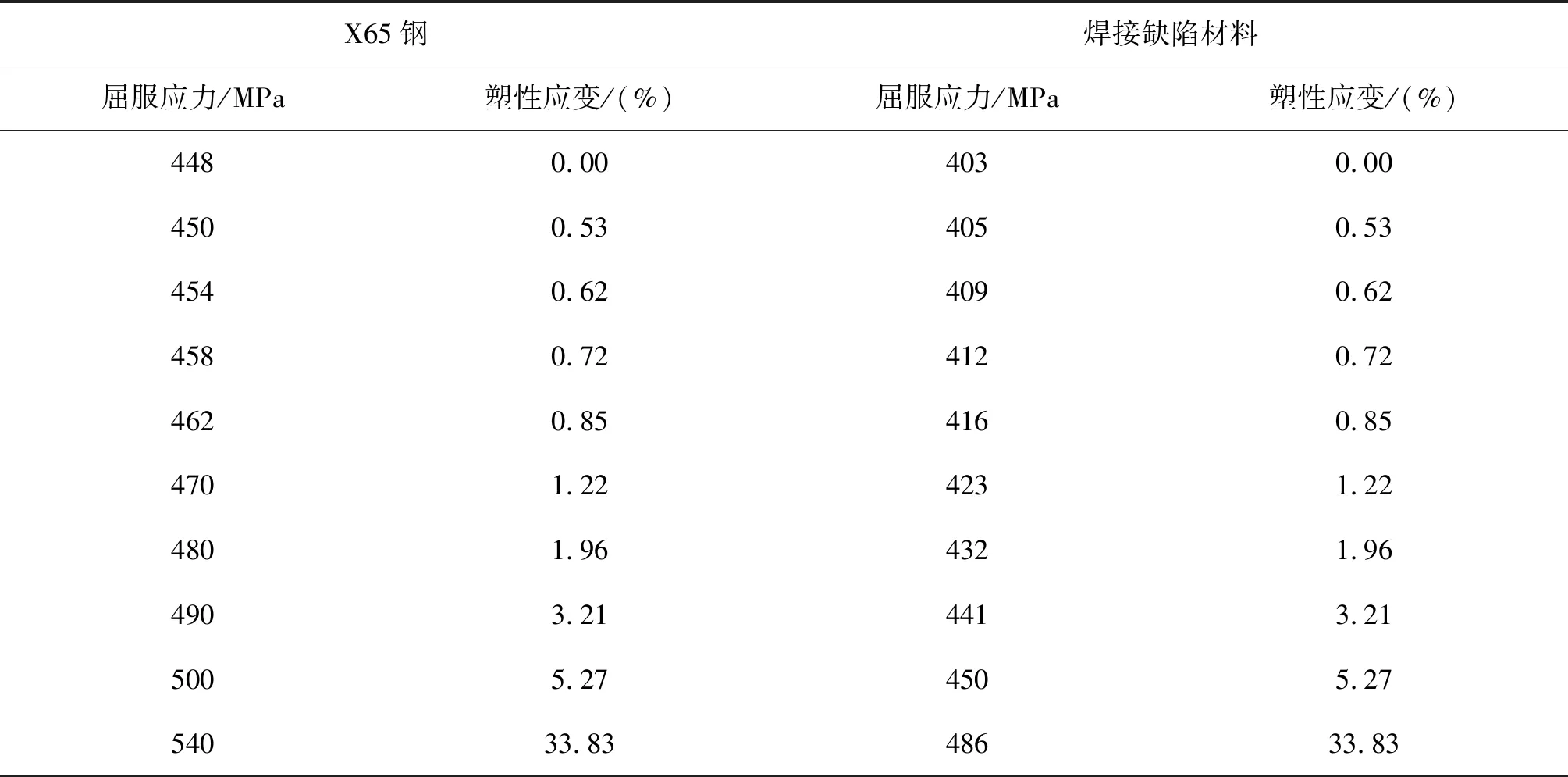
表2 兩種材料應力-應變關系Tab. 2 Stress-strain relationship for two materials

通過拉伸試驗確定材料應力-應變曲線時，考慮試件在拉力作用下原長不斷增加的應力-應變曲線稱為真實應力-應變曲線，不考慮試件原長變化的應力-應變曲線稱為工程應力應變曲線，兩者之間的差別在于應變的計算方法不同。真實應變與工程應變轉換方程如下：

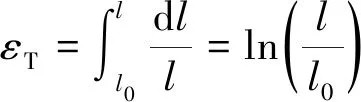
(2)

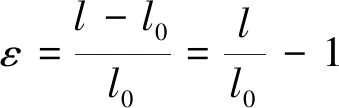
(3)

εT=ln(1+ε)

(4)

式中：εT為真實應變，ε為工程應變。

令管道A端與卷筒圓心耦合，卷筒以0.1 rad/s的角速度轉動并帶動管道上卷及退卷；管道F端僅在垂直方向存在約束，水平方向受恒定回拉力T作用，其中T=0.01T0(T0為管道屈服應力與管道截面積的乘積)，如圖2所示。管道應用S4 shell單元模擬，將AB管段和EF管段環向劃分為32個網格，軸向每長D為一個網格。由于主要研究管道材料性能缺陷引起的應力和變形，故取焊接處前后各3D的管段(BE段)為測試管段，對該段采用更精細的網格劃分，環向上仍劃分32個網格，軸向每D長劃分10個網格，其網格大小為普通管段的1/10。卷筒由解析剛體模擬，卷筒與管道之間定義為面面接觸，卷筒面剛度較大為主面，管道面剛度較小為從面，接觸剛度恒定，主面可以穿透從面，從面不可以穿透主面。

圖2 卷有限元模型Fig. 2 FE model of pipe reeling

2.2 有限元結果對比分析

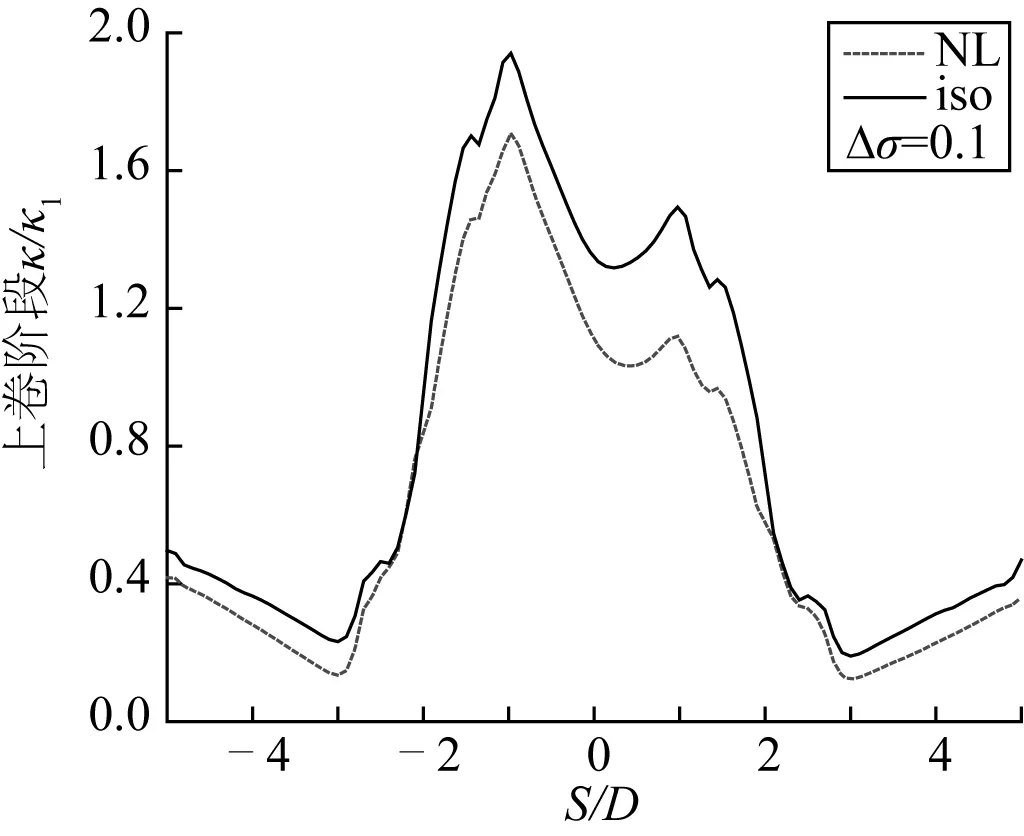
圖3 上卷階段兩種本構模型下的管道曲率Fig. 3 Curvatures under two kinds of constitutive models during reeling

分別使用各向同性硬化模型及Ramberg-Osgood材料模型進行卷管鋪管的有限元模擬，提取上卷及退卷階段管道沿管長s方向上的曲率、等效塑性應變及殘余橢圓度。根據管道變形后的節點坐標計算管道曲率k，對其進行標準化后得到上卷階段管道局部曲率k/k1(其中k1=t/D02)，如圖3所示，其值可代表卷管期間管道構型的變化。使用各向同性硬化模型進行模擬時管道曲率峰值為2.0左右，采用非線性運動硬化模型所得管道曲率峰值為1.7左右。圖4為管道等效塑性應變ε的分布圖，圖4表明各向同性硬化模型所得的等效塑性應變峰值為0.055左右，非線性模型所得的等效塑性應變峰值為0.046左右。圖5為管道橢圓度ΔD/D的分布圖，各向同性硬化模型的結果顯示上卷完成后管道的殘余橢圓度最大值為5.5%左右，而非線性運動硬化模型的結果為4.7%左右。

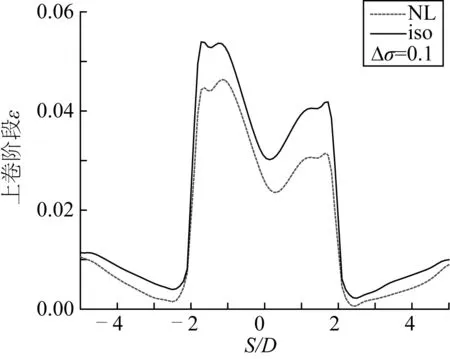
圖4 上卷階段兩種本構模型下的管道等效塑性應變Fig. 4 Pipe equivalent plastic strain in two kinds of constitutive models during reeling

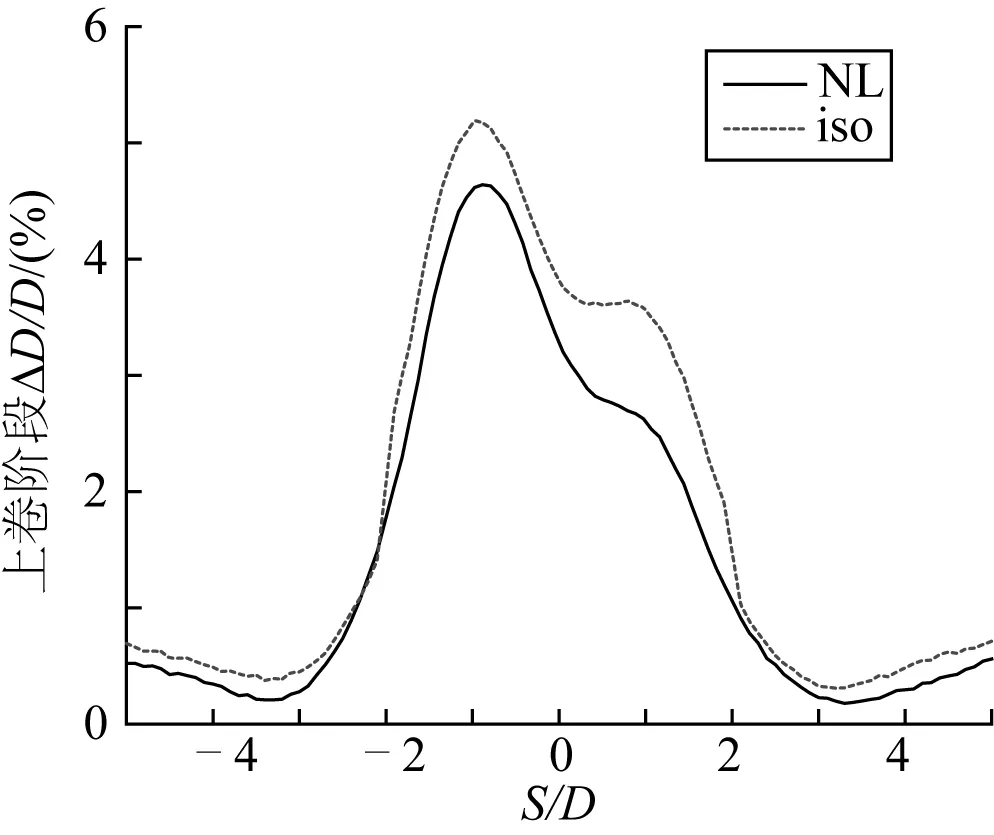
圖5 上卷階段兩種本構模型下的管道橢圓度ΔD/DFig. 5 Pipe ovality ΔD/D in two kinds of constitutive models during reeling

另外，各個曲線在力學性能不均勻的管段處均存在明顯波動，說明上述兩種模型均可模擬由于管道卷曲及管段力學性能不均勻性所引起的局部曲率、殘余橢圓度及等效塑性應變沿管長方向的變化，但在上卷階段各向同性硬化模型所預測的結果均較Ramberg-Osgood本構模型所得的結果稍大，且在管道焊接處及其鄰域管段的局部波動也更為明顯。但在上卷階段，兩種材料本構模型所得結果的差異并不大，不能準確評估哪種模型能更為真實地模擬管道在卷管安裝鋪設過程中的力學行為。

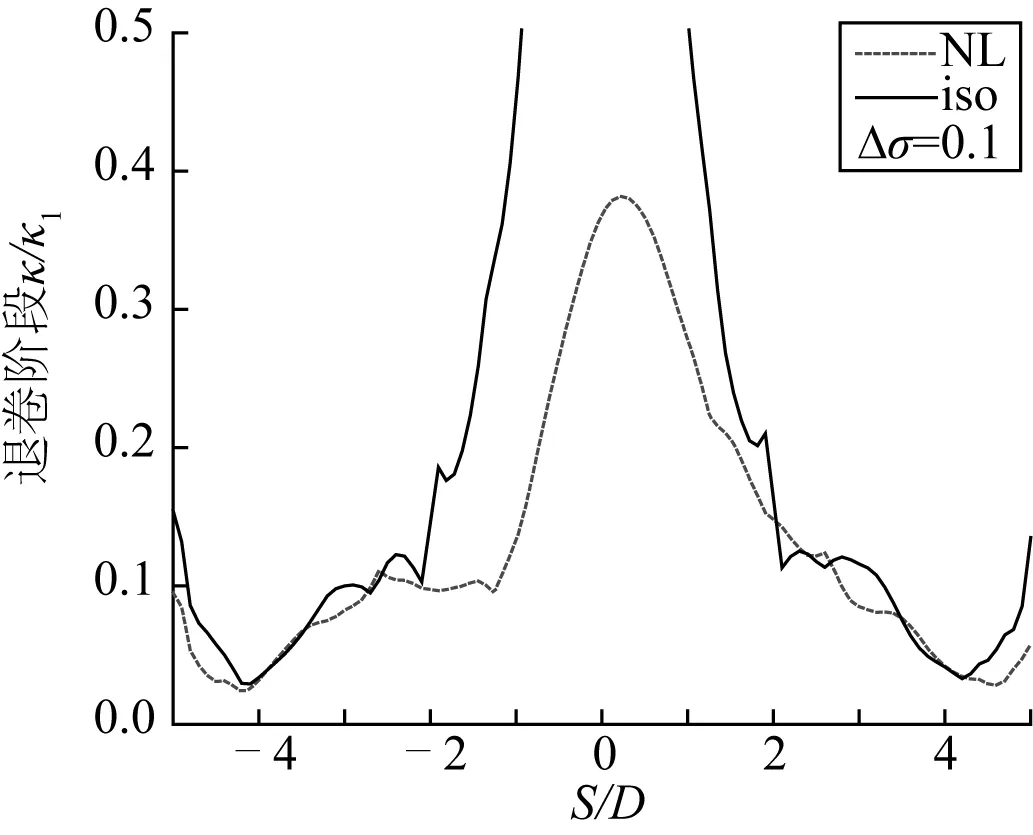
圖6 退卷階段兩種模型下的管道曲率Fig. 6 Pipe curvatures in two kinds of constitutive models during unreeling

圖6為退卷完成后管道的局部曲率。使用Ramberg-Osgood模型分析得到的結果顯示退卷階段管道的局部曲率較上卷階段有所減小，這是由于管道在退卷過程中被拉直，此時曲率峰值為0.37左右。圖7為管道等效塑性應變的對比，圖7表明管道等效塑性應變在退卷完成后將會增加，其峰值為0.095左右。圖8表明退卷后管道殘余橢圓度沿管長的分布情況與曲率及應變相似，其最大值為1.7%左右；但使用各向同性硬化模型模擬所得的結果中，管道的局部曲率、橢圓度及應變均顯著增加，其峰值遠遠大于非線性模型結果曲線的峰值。DNV規范[13]中規定管道橢圓度不可超過3%且管道累積應變不可超過0.3%，故其最大值已大大超過DNV規范所規定的標準值，按其仿真結果管道將在退卷期間發生局部屈曲。總之，在退卷階段兩種模型所得結果之間存在更為顯著的差距。

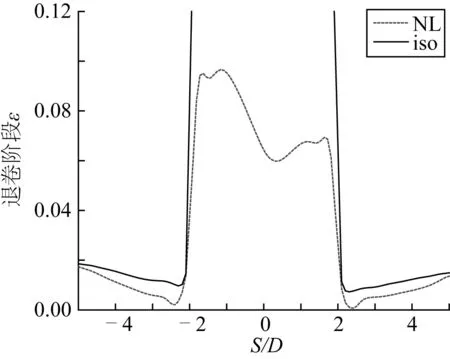
圖7 退卷階段兩種模型下的管道等效塑性應變Fig. 7 Pipe equivalent strain in two kinds of constitutive models during unreeling

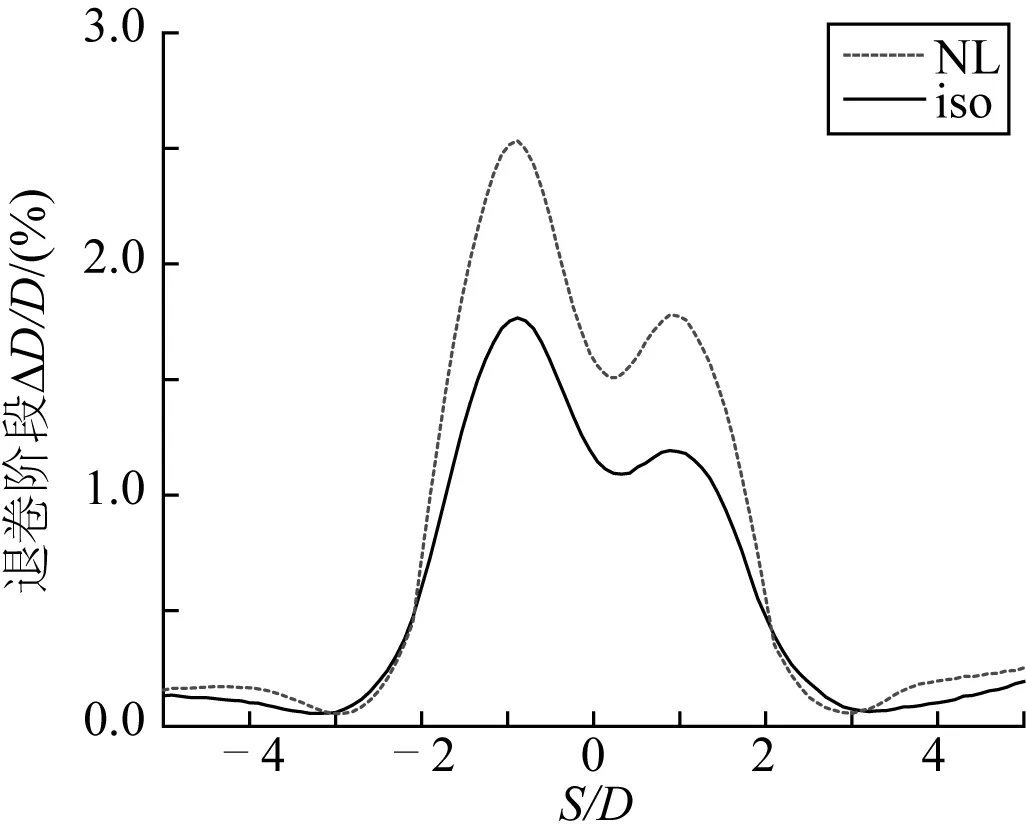
圖8 退卷階段兩種模型下的管道橢圓度ΔD/DFig. 8 Pipe ovality ΔD/D in two kinds of constitutive models during unreeling

上述結果表明，使用各向同性硬化模型對卷管安裝中管道的力學行為進行模擬時，將得到管道在反向加載過程中出現失穩的結論，不符合管道在卷管鋪管中的實際力學行為；而使用Ramberg-Osgood模型進行模擬所預測的結論更為貼合管道真實的力學行為。如圖1所示，這種現象是由于各向同性硬化模型不能真實模擬退卷過程中反向加載階段管道材料響應的非線性變化，忽略了Bauschinger效應，以致得出不合理的結論。

因此，各向同性硬化模型并不適用于卷管安裝管道設計的數值仿真，使用Ramberg-Osgood模型可以較為真實地模擬卷管安裝中管道的力學行為。

3 管道力學性能不均勻性對卷管安裝的影響分析

應用于海上油氣生產的管道材料均按其規定的最小縱向屈服應力進行生產，但在管道生產過程中熱機械加工操作如相鄰管道的焊接結合等，將導致管道材料的力學性能出現不均勻性，其屈服應力沿管長方向也將存在一定變化。因此，管道焊縫處及其鄰域管段的力學性能不均勻性難以避免，在卷管法安裝管道設計中必須加以考慮。但由于環焊縫處及其熱影響區之間的作用相當復雜，因此將管道力學性能的不均勻性理想化為管道材料屈服應力的顯著差異進行研究。

為研究管道在焊接處及其鄰域管段存在的力學性能不均勻性對卷管安裝過程中結構安全的影響，使用與前述所建模型相同的方式，分別建立四段在焊縫及鄰域管段具有不同屈服應力的管段，其屈服應力分別為σ1=0.95σ、σ2=0.90σ、σ3=0.85σ、σ4=0.80σ，并使這四段管段在0.01T0的回拉力水平下進行上卷和退卷。

圖9是四種屈服應力下管道沿管長方向局部曲率的變化。圖9中焊接處屈服應力為σ1時，管道局部曲率較小，在上卷階段達到峰值，僅為0.8左右；而屈服應力為σ2時，管道局部曲率稍有增大，最大值為1.6左右，此兩種情況下局部曲率的波動均不甚明顯。而當屈服應力為σ3和σ4時管道局部曲率在焊接處出現幅度極大的波動，當屈服應力為σ4時甚至躍出縱軸幅值，在退卷完成后管道殘余曲率仍然很大，說明此時管道已不能被完全拉直。

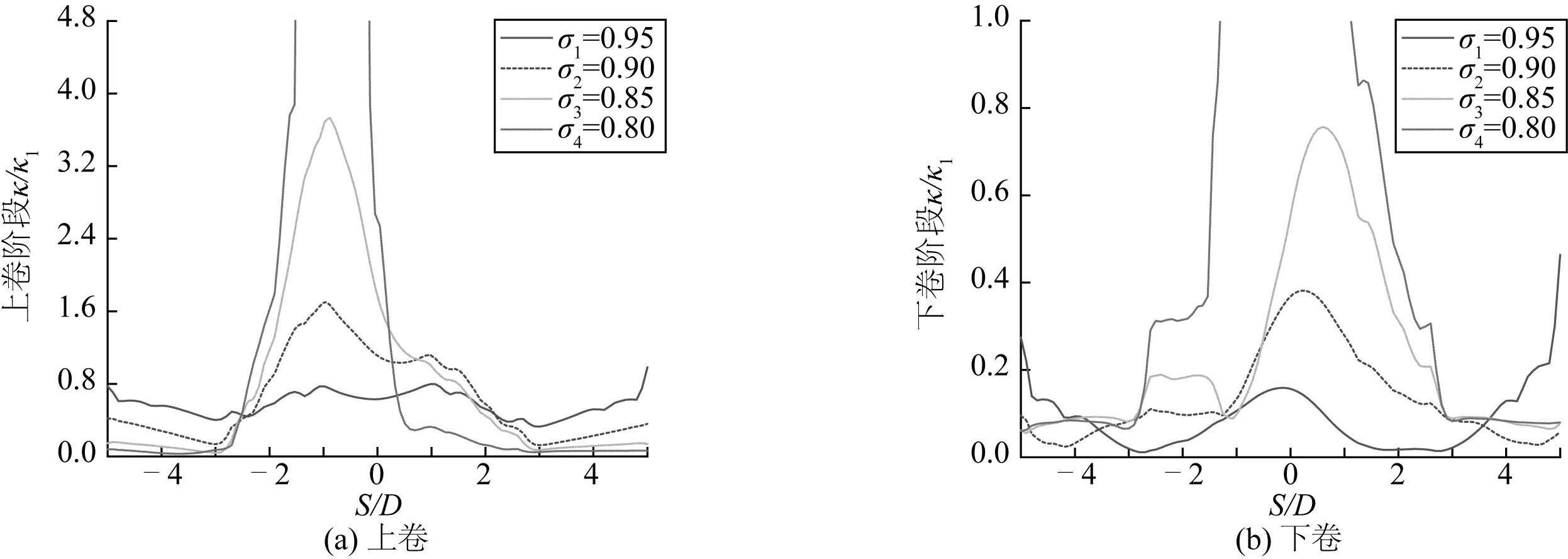
圖9 四種屈服應力下管道曲率Fig. 9 Pipe curvatures under four kinds of yield stresses

圖10為四種屈服應力下管道沿管長方向的等效塑性應變。圖10表明四種情況下退卷后管道的等效塑性應變均較上卷階段有所增加，屈服應力為σ1時，管段最大等效塑性應變值分別為0.04左右，此時管段力學性能不均勻性的影響較小；屈服應力為σ2時，最大值為0.09左右；屈服應力為σ3時，最大值為0.18左右；而屈服應力為σ4時，等效塑性應變峰值大大增加，此時管段于焊縫處發生顯著的局部變形。

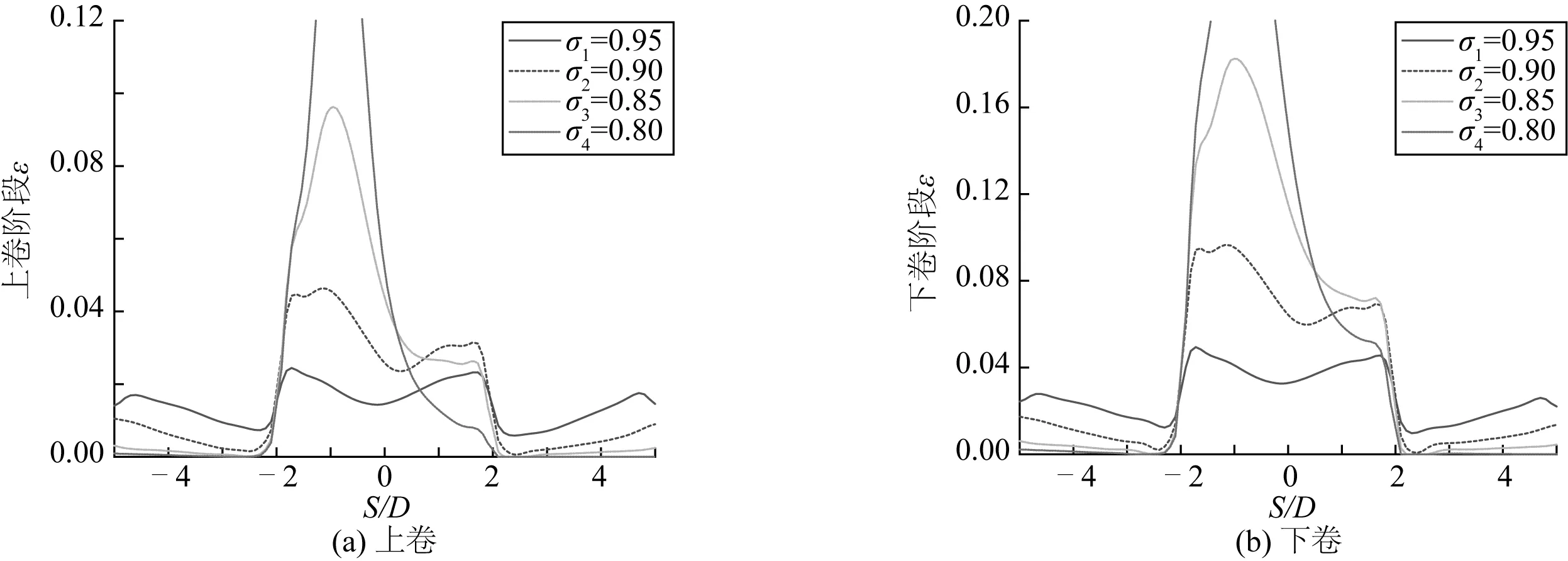
圖10 四種屈服應力下管道的等效塑性應變Fig. 10 Pipe equivalent plastic strain of the pipe under four kinds of yield stresses

圖11為四種屈服應力下管道在上卷和退卷過程中的橢圓度。圖11表明管道橢圓度變化趨勢與局部曲率及等效塑性應變相同。隨著焊接處管段屈服應力σ的減小，管道在上卷和退卷完成后的殘余橢圓度越來越大。

由此可見，屈服應力為σ1時，焊接處管段力學不均勻性對曲率、應變及橢圓度的影響均很小。屈服應力為σ2時，三組曲線均在管道力學性能不均勻處產生更為明顯的波動。而當屈服應力較原始值差值達到0.20σ時，從圖12中的管道變形圖可以看出管道已產生較為明顯的凹陷。顯然，在此情況下管道焊縫處的局部彎曲剛度已經下降，導致焊縫處及其鄰域管段脫離卷筒，管道局部曲率存在顯著波動，同時橢圓度ΔD/D也大大增加，局部等效塑性應變最大值已超過20%。此時管段力學性能不均勻性已大大影響其結構完整性，很可能導致管道在后續服役中出現壓潰、破裂等嚴重破壞現象。

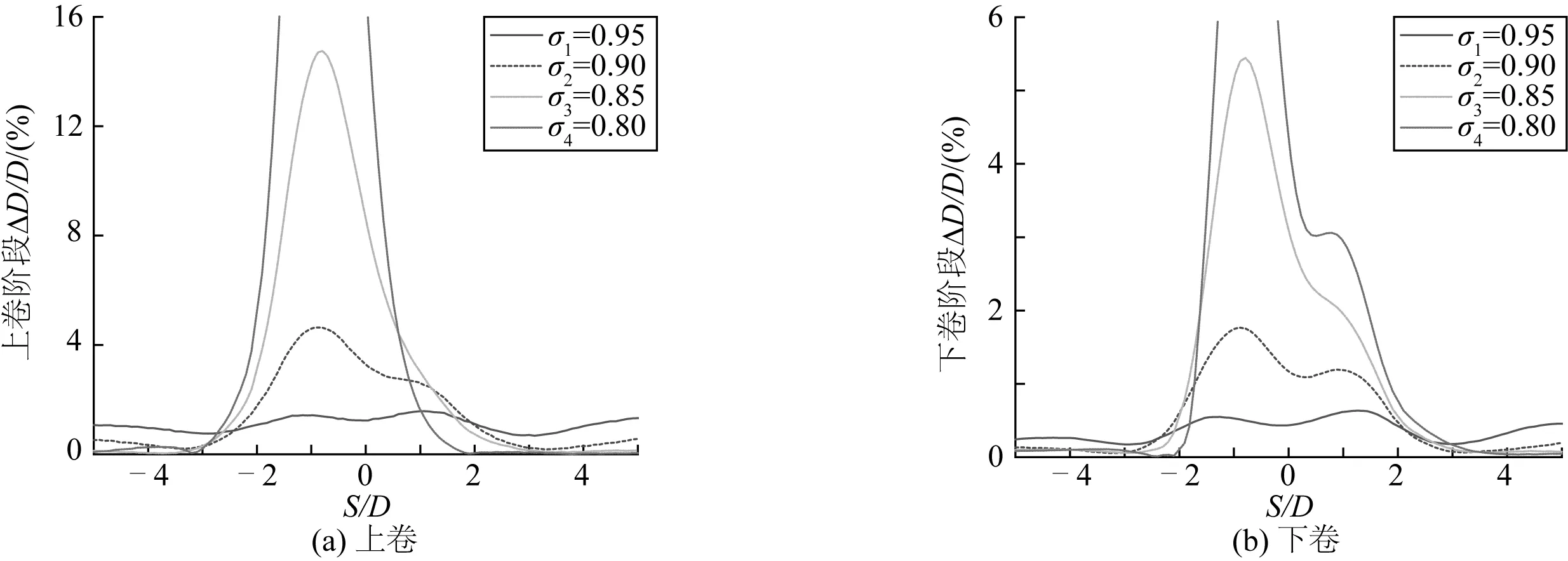
圖11 四種屈服應力下管道的橢圓度ΔD/DFig. 11 Pipe ovality ΔD/D under four kinds of yield stresses

圖12 屈服應力σ4=0.80σ時管道變形Fig. 12 Pipe deformation when yield stress is 0.80σ

此前Dailey等[14]證明鋼柱在焊縫及其熱影響區域存在應力集中，Netto等[15]通過原型測試驗證鋼管在焊縫處易產生局部變形乃至斷裂。而本文研究表明鋼質管道在焊縫缺陷及其鄰域管段存在力學性能不均勻性，將對卷管安裝中管道的安全性能產生不良影響，且管道力學性能不均勻性越強，其結構完整性及安全性能越差，與Dailey和Netto等人的研究結論相一致。因此，采用卷管法安裝管道對管道的焊接性能有著更高的要求。

4 結 語

由于熱加工影響，管道材料性能將在焊縫處及鄰域的熱影響區管段出現差異，即管道存在力學性能不均勻性。首先采用各向同性硬化材料模型與Ramberg-Osgood材料模型建立ABAQUS有限元模型，進行卷管仿真模擬，通過仿真結果的對比分析，確定卷管安裝數值模擬中應選用的合理材料模型。基于此，研究焊接所致的管道力學性能不均勻性對卷管安裝的影響，研究結果表明：

1) 在卷管鋪設的數值模擬中，使用Ramberg-Osgood模型能夠更為真實地模擬管道的力學行為，獲得更接近真實值的管道力學響應結果，而使用各向同性硬化模型將導致仿真模擬結果出現嚴重失真，不宜采用。

2) 焊接所致管道材料力學性能的不均勻性足以對卷管安裝管道設計產生影響。該缺陷將造成管道應力出現顯著增加，從而導致管道在缺陷處產生較大的局部變形，造成管道出現局部屈曲甚至壓潰、破裂，且管道力學性能不均勻性的水平越高，對管道結構完整性造成的不良影響也越大。因此，采用卷管安裝的管道應該盡量提高焊接質量，減少焊接不均勻性。