強化幾何直觀和代數推理，發展學生思維

【教學內容】

這節內容可安排在人教版數學七年級上冊第三章第一節“從算式到方程”內容之前，也可安排在北師大版數學七年級上冊第五章第一節“認識一元一次方程”之前，可作為一元一次方程的起始課。本節課由“陳莉紅陽光數學名師工作室”成員付敏老師和胡德才老師參與設計并進行教學實驗。

【設計理念】

方程模型是初中階段代數思維的第一個模型，通過方程的學習實現從算術思維到代數思維的轉化，這是一個高度抽象的過程。如何幫助學生順利地實現思維的過渡，需要在教學過程中加強幾何直觀和代數推理。一元一次方程這一章的教學有兩個問題：一是從算式到方程的過渡效果不理想。學生習慣了小學的算術法，認為算術法能快速求出答案，而用方程求解時需要寫較多步驟，對引用方程解決問題的必要性沒有真正理解接受。二是學生學完了一元一次方程后，遇到稍復雜的情境就不會列方程。而這種現象的本質是因為沒有真正理解列方程的關鍵是要尋找等量關系，要在教學情境中發現量、表達量，尋找等量關系再列方程。為了解決學生從算術到代數思維過渡的問題，筆者特意設計了這節課，并在這節課中有效滲透代數推理及充分運用框圖幫助學生理解、強化幾何直觀的作用。

【教學目標】

1.體驗算術法和代數法都是解決實際問題的常用方法。

2.感悟同一教學情境中算術法和代數法的聯系與區別，并認識到運用代數法解決問題的必要性。

3.在思維上接受算術法向代數法這種思考問題方式的轉變，并對代數法解決問題產生心理認同。

4.初步形成運用列代數等式法的解題意識和解題素養。

【教學重點、難點】

重點：感悟算術法與代數法解決問題的特點，體驗算術法與代數法的聯系與區別。

難點：讓學生感悟運用代數方法解決問題的必要性，運用代數方法表示未知量及建立等式。

【設計思路】

1.從思維發展的角度，讓學生真正理解從算術到代數的必要性，感悟算術與代數兩種思維的區別與聯系，為下節課從算式到方程打下堅實的基礎。

2.在表達未知量及未知量之間的關系時，滲透幾何直觀思想，利用圖表或者框圖等可以幫助學生理解問題情境的輔助工具，直觀表達;利用字母表示未知量，利用推理尋找量與量之間的關系，實現數學抽象，進而達到數學建模的效果，并將這種做法一直貫穿在一元一次方程整章內容的學習過程中。

【教學過程】

一、創設情境，激發興趣

民間歌謠：“雞鴨共一欄，雞為鴨之半。

八鴨展翅飛，六雞在生蛋。

再點雞鴨數，鴨為雞倍三。

請你算一算，雞鴨原若干？”

教師先讓學生解釋歌謠的意思并提問。

師：請同學們想一想歌謠中總共有哪些量？已知量、未知量分別是什么？

生1：一開始雞和鴨的只數，飛出去鴨的只數和躲起來的雞的只數，后來欄圈里雞和鴨的只數。

（若生1說不全，可讓其他學生補充。）

師：同學們，這些量之間有什么關系呢？

生2：一開始雞的只數是鴨的一半，后來鴨的只數是雞的3倍。還有飛出去鴨的只數和躲起來的雞的只數是固定的，分別為8只和6只。

生3：一開始雞的只數減去6等于后來雞的只數，鴨的只數減去8等于后來鴨的只數。

師：現在知道了這些量及它們之間的關系，如何求一開始雞和鴨的只數呢？

生4：雞為鴨的一半，可知鴨的只數為偶數，雞的只數至少為7只，那么我就從雞的只數一個一個地試。

師：這個同學是假設雞的只數分別為7，8，9，10，然后一個一個地計算檢驗，他這樣做可以嗎？

生：可以。

師：如果題目變為“今有一群雞鴨被關在一個欄圈里，已知雞為鴨的一半。主人在清點雞鴨時，發現有20只鴨飛出欄外了，又有40只雞躲起來生蛋，這時清點得鴨的只數為雞的5倍，請你計算雞、鴨各有多少只。”你還會做這道題嗎？請同學們試試吧！

師：請哪個同學分享下他的解題思路。

生5：數據較大，一個一個地試要試好久。

生6：我也是，還沒試出來。

……

師：這道題能試出來嗎？

生：能。

師：要試多長時間才能找到答案？

生：不知道。

師：有沒有哪個同學能列算式解答？

（學生沉默中……）

師：在探究過程中，我們一個一個地枚舉嘗試，需要時間長且無法判斷有沒有其他的解，尤其是題目條件的數量變大后，更是增加了枚舉的難度，列算式又想不到，那怎么辦呢？

生：題目中的量太多了，關系也復雜，感覺腦子不夠用了。

師：我們就先想想用什么方式能把各個量之間的關系表達出來，那樣是不是思路更清晰一些呢？

生：好呀！

師：請同學們注意看題目條件，題目中有幾個未知量，彼此之間有什么樣的數量關系，哪個同學來回答？

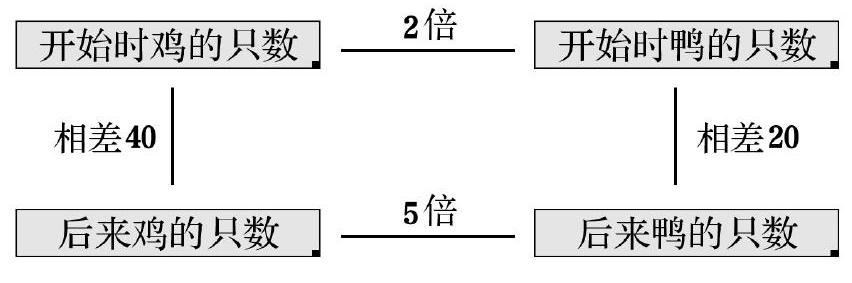
教師引導學生用框圖的形式把未知量之間的關系表達出來（如下圖）：

師：請同學們繼續思考，如果我們用字母來表示未知量，需要用幾個字母就可以把所有的未知量全部表示出來？

生：只需要用一個字母就可以了。

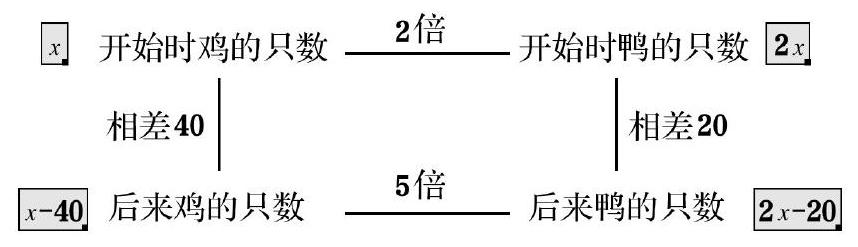
師：我們可以設任意一個量為x，比如設開始時雞的只數為x只，請問你們能把其他3個未知量用x的代數式表達出來嗎？

（教師巡視、觀察，拍下學生的解答過程，上傳屏幕展示。）

師：請同學們繼續思考，圖示中的每一個量可以有幾種不同的表達方式？比如就選后來鴨的只數這個量，還有不同的表達方式嗎？

生：有，后來鴨的只數可表達為：5（x-40） 。

師：很好，我們發現了后來鴨的只數這個量可以有兩種不同的表達方式，所以它們應該是相等關系，可以列出等式：2x-20=5（x-40）。

師：我們通過設未知數、列代數等式的方法解決了問題，今后我們會學習如何求解這個等式并能計算出x=60。

師：大家覺得這個方法和以前的解法有什么不同？

生：用枚舉嘗試法能成功求解問題，如果數據很大，要嘗試很久才能找到答案;列算式是逆向思維，關系很復雜，量多的時候就很難理清思路、直接列出算式。

師：你說得非常對，以后遇到類似的問題時，你會怎么辦？

生：我會嘗試用列代數等式的方法解決問題。

師：好極了，我們又學會一種解決實際問題的新方法。

【設計意圖】

在本教學環節中，教師首先以一首民間歌謠作為情境引入新課，一方面增強趣味性，另一方面歌謠中出現的量較多，關系較復雜，學生不易由算術法直接得出答案，從而產生認知沖突，凸顯代數法的必要性。然后教師在解決問題的過程中，有意識地引導學生通過表格、框圖等形式直觀地表達量與量之間的關系，在代數中滲透幾何直觀。用字母表示各個量實現第一次數學抽象，尋找等量關系實現第二次數學抽象。最后通過對問題的討論探究，讓學生親歷枚舉計算、列算式和列代數等式的解題過程，體驗出各種解法的優劣，從心理上傾向認同列代數式解決問題的思維方式。“算術方法”表現為“逆向思考”，它只含已知數，但很難一步到位，思維要求較高。

列代數等式時不急著求出未知數，而是先尋找各量之間的關系，找到同一個量的不同表達方式，再設未知數表達出等量關系。它思路清晰，易列出含未知數的等式，表達題意準確自然，易于學生理解接受，在教學過程中培養了學生的數學抽象、數學建模、邏輯推理等數學核心素養。

二、活動探究，鞏固應用

例1? 有甲、乙兩堆小球，甲堆比乙堆多，乙堆有6個小球，如果按照以下規則挪動小球，第一次從甲堆拿出和乙堆同樣多的小球放到乙堆，第二次從乙堆拿出和甲堆剩下的同樣多的小球放到甲堆，請解答以下兩個問題：（1）若假設第一次挪動以后，甲、乙兩堆小球一樣多，甲堆原先有多少個小球？（2）若假設第三次挪動以后，甲堆比乙堆少6個小球，甲堆原先有多少個小球？

師：請同學們先做第（1）問，哪個同學說說，你是怎么算的？

生1：我是用算術法做的。第一次移動后，乙堆加了6個球，甲堆少了6個球，甲堆剩下的球正好等于乙堆的12個球，用逆推法就可以列出算式了。

生2：我是用列代數式的方法做的。設甲堆原先小球數為x個，第一次移動后，乙堆12個球，甲堆x-6個球。這兩堆一樣多，讓這兩個代數式相等就可以了。

師：不論是算術法還是代數式，都把移動后甲、乙兩堆小球數目的變化規律搞清楚了，用逆推法可以直接求出小球數目，用列代數式的方法可以把等量關系表達出來。非常好，那么我們再繼續解答第（2）問。

（教師巡視學生答題情況。）

師：第（2）問還能用算式法做嗎？

生3：次數越多，關系越復雜，列算式比較困難了。

師：既然列算式比較困難，那我們試試代數法。

師：為了把所有量都表達出來，而且它們之間的關系還能一目了然，我們可以怎么做？

生4：我們可以畫表格，或者用框圖的形式表達出來。

師：同學們試一試自己畫表格。

（教師幫助學生一起畫表格。）

師：表格畫出來了，哪個同學說說表格里的答案？

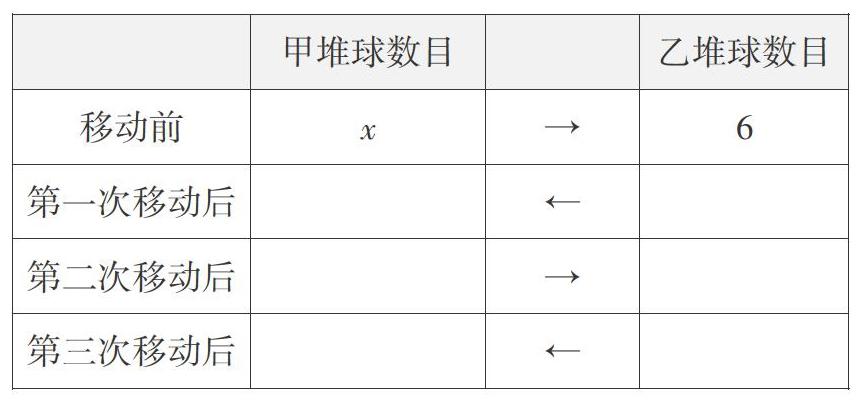
生5：我是這樣做的（如下表）。

師：太棒了，請你和大家一起分享下是怎么得到答案的？

生5：我注意到，每次移動前后球的總數是x+6，是恒定不變的，所以每次移動后，我先確定翻倍后的那一堆球的數目，再用總數減去翻倍后的那一堆球的數目就得到了余下球的數目。

師：很好，我們可以順著題意直接列出來，也可以抓住變化中不變的量（小球總數不變）來幫助我們找到關系，列出代數式。

師：接下來可以根據什么關系列等式呢？

生6：第三次挪動以后，甲堆比乙堆少6個小球。

師：誰能說出解答過程？

生7：2（x-6）-[12-（x-6）]= 2[12-（x-6）]-6，解得x =12。

師：非常好！請同學們體會代數法的運用策略：尋找未知量、表達未知量和建立等式。

【設計意圖】

在本教學環節中，教師圍繞移動小球的游戲活動展開探究，設置兩個問題，由易到難，由簡單到復雜，在解決問題（1）時，讓學生體會到算術法和代數法都是解決問題的基本方法。在解決問題（2）時，由于關系復雜，用算術法會遇到障礙，自然產生認知沖突，體會到代數法的必要性，使得從算術到方程的過渡顯得非常自然。在表達復雜關系的量的時候，教師引導學生畫表格來幫助理清思路，在代數推理中加強了幾何直觀，在學生表達第一次移動、第二次移動、第三次移動的小球數目過程中，自然地運用到了代數推理，在潛移默化中培養了學生的代數思維。

三、課后閱讀，感受數學文化

師：請同學們課后閱讀有關材料，初步了解代數法發展、演變、進步的過程，并認識一些為數學癡迷、為數學發展和進步作出巨大貢獻的偉大數學家們。

師：請同學們到網上搜索古代元朝時著名數學家朱世杰的故事，并搜集與本章相關的內容與大家一起分享。

師：請同學們了解關于希臘數學家丟番圖的故事，做一做丟番圖墓志銘上的數學題。

【設計意圖】

在本教學環節中，教師讓學生搜索古代元朝時著名數學家朱世杰的故事以及希臘數學家丟番圖的故事，滲透數學文化，落實立德樹人的目標，有效地發展學生數學核心素養。

（作者單位：江西省教育廳教學教材研究室）