例談教學中的“圈養”和“散養”

張仁進，江蘇省南京市鼓樓區教師發展中心小學研訓部副主任，高級教師。先后主持了“小學數學課堂中先研后教的范式”“小學數學建構按需樂學、大空間下的學與教動態平衡”等省市規劃課題并順利結題;多次參加市區教學基本功比賽并獲一等獎，曾獲南京市課堂教學競賽一等獎，開辦區級以上學術講座五十余次，已發表或獲獎的論文、案例近60篇。

[摘? ?要]長期以來，教師在課堂教學中一直朝著流暢、細膩、精致的方向努力，也的確創造了很多精彩的設計。然而在更關注“學”，更關注個別化發展，更關注學生綜合能力提升的當下，教師應努力使教學從“圈養”走向“散養”，使核心素養的培養真正落地。

[關鍵詞]圈養;散養;素養;小學數學

“圈養”本是一個畜牧業名詞，意為關在圈里飼養;“散養”則是指在圈外分散飼養或放養。對人類來講，雖然散養動物更健康、營養價值更高，但圈養動物產量更高、更方便。在課堂上，也存在大量類似“圈養”的教學。比如，很多教師更多地追求教學中行云流水般的過程、細膩精致的手法、令人驚艷的預設等，于是課堂該有的樣子在課前就已經被嚴格而詳細地設定好，只要按照既定“劇本”一環接一環地有序推進，就能熱熱鬧鬧而又順利地完成教學目標。但很多學習過程也因為教師“無微不至”的精細化處理或鋪墊而失去了應有的挑戰性，這樣的教學就如同“圈養”。

我國臺灣語文教育專家李玉貴曾說：“我在大陸上課很緊張，因為這里見不得冷場。”也有其他臺灣教師表達過類似的感慨，如“大陸的教師太會教了”“大陸的課堂是不是一定要教出點東西來才罷休”[1]。的確，我們的很多教學還在某種程度上“執著于教”，教師在課堂上的急功近利依然或多或少地存在，有更多刻意圈養的意味，缺少自由散養的信心。在此，將以蘇教版五年級數學“除數是小數的除法”一課為例，介紹筆者的兩次教學設計，解讀教學中的“圈養”與“散養”。

一、第一次教學設計：“圈養”舉例

1.讓學生在具體情境中初步感悟算理

一是先獨立思考再交流。在教學“除數是小數的除法”一課時，教師讓學生先獨立思考，然后再小組交流以下問題。

（1）用手機發短信0.1元一條。口答：1.5元可以發多少條短信？請列出算式并簡要地寫出你是怎么想的。

（2）用彩繩制作中國結，每0.25米可制作一個。現有0.75米的彩繩，可以制作多少個中國結？請列出算式并簡要地寫出你是怎么想的。

二是全班分享。教師在學生展示列式時強調其數量關系式，在學生敘述算法時強調兩種方法：一種是化成小單位“角”或“厘米”計算;另一種是利用商不變的性質，除數、被除數同時乘10或100后再計算。

三是比較提升。引導學生比一比兩題的算式與以前學過的有何不同，然后教師揭示并板書本課的課題“除數是小數的除法”。讓學生比較計算每一題的兩種方法有何共同點，如“都是轉化成整數來計算的”，教師再板書“轉化成整數”。

四是鞏固算法。教師請學生口算以下題目：0.8÷0.4=（）;0.36÷0.06=（）;0.125÷0.025=（）。

五是反思總結。教師請學生談一談“除數是小數的除法應如何計算”。

2.讓學生在對比反思中進一步明晰算法

教師先出示一個數學問題：一只鴨重2.696千克，一只雞重0.8千克，鴨的質量是雞的多少倍？然后用下列步驟引導學生對比和反思，明晰算法。

一是獨立思考。思考：這個問題中的列式要怎樣轉化而商不變？只寫出過程即可（見圖1）。

二是組內交流。請學生在小組內觀察并討論：觀察組內每人轉化得對不對，如果發現有錯誤的，在組內開展互助，糾正錯誤;如果同組內出現了不同形式的正確轉化，討論哪一種轉化更好。

三是全班展示分享。先判斷哪些轉化正確，再比較哪種轉化更好。如圖1的三種轉化（其中包括錯誤示例）。

四是回顧反思。請學生再談一談對“除數是小數的除法”有什么新的認識。為了使學生進一步明確小數點移動的位數取決于什么，讓他們再試著說一說以下各題應如何轉化。

0.035÷0.05=（ ）;0.0024÷0.006=（ ）;2.6÷2=（ ）;7.98÷4.2=（ ）

顯然，在以上主體設計中不乏閃光點。如層次清晰，教學環節整體上比較簡約;重視激活學生生活經驗，試圖為學生找到理解新知的附著點;重視學習方式，努力實現教師課堂的“讓、等、退、隱”等。但仔細琢磨整個教學過程，仍不難發現其中“圈養”的痕跡。

二、分析第一次教學中的“圈養”

1.與兒童天性不相適的封閉性

在拉丁文中，“兒童”一詞意味著自由。蒙臺梭利認為“兒童是上帝派來的密探”。蘇霍姆林斯基認定兒童是探究者。探究的天性使兒童產生對周圍世界的驚異，因而兒童是哲學家。好奇心、自由自在、探究未知是兒童的天性。而圈養之所以被稱為“圈養”，是因為它限定了范圍，限制了自由。在當下的課堂教學中，可以清晰地看到很多“圈養”的痕跡。如上例中，教師在讓學生感知算理的環節，從具體情境到最后口算鞏固，除數、被除數的小數位數都是相同的，顯然教師的教學目標就是想先把學生“圈”在“轉化成整數”這個階段。

2.與學習過程不匹配的切割感

在圈養條件下，無論圈中動物的飯量大小，是否饑渴難忍，進食的時機都不能像散養那樣自由，而是要由飼養者統一掌控，定點定時地喂食。在教學中，這一特點體現為刻意的強化與分割。上例中，教師在其創設的兩個問題情境中都孕育了小數除法的算理和算法，再通過全班分享、提升概括環節，讓學生初步掌握了小數除法的計算方法——移動小數點，將被除數、除數全部轉化成整數。不僅如此，教師最后還通過三道口算題鞏固算法、強化認識，以使學生形成更強的思維定勢，即“要將除數、被除數統統轉化成整數”。從某種角度來講，這種強化具有一定的“誘騙性”。在第二個讓學生明晰算法的環節，教師將重點放在了“糾偏”上（也是一種深化）：轉化時不一定要將除數、被除數統統轉化成整數，只需要按照商不變的規律將除數轉化成整數即可。而這個“偏”的原因正是上一階段“喂食”的結果。這樣，對于“除數是小數的除法”的計算法則，學生經歷了兩個階段才完成。

事實上，從學習者的角度思量，學習的過程應該是一個連貫的過程，但并非所有學生都必須經歷這樣的過程。少數學生可能在課前已經知曉算法，大多數學生在這些學生的啟發或引領下完全可以自己理解并掌握，個別“學困生”只要花些時間也完全能夠“跟上來”。更重要的是，這段跋涉的過程無論對哪種水平的學生來說，都是一次可貴的“學習之旅”。然而，教師因為怕學生出錯，怕課堂亂，怕課堂生澀冷清不熱鬧，將一個連貫的學習過程人為地分割成了兩個環節，將學習目標封頂，不許學生越雷池一步。

3.與兒童發展相背離的溫室效應

被圈養的動物雖然生活空間封閉，但是有固定的場所遮風擋雨，有人定時投喂，久而久之，它們的天性或求生能力就會退化，一旦開圈放生，在自然界將難以生存。教學中的“圈養”也同樣如此。學習是一個連貫的過程，任何一個問題的解決、概念的建構、技能的形成都必須經過學習者的入境、聯結、建構、重組才能實現。但是，教師因為要“分散難點”“穩步分層推進”，便將一個相對完整的教學活動過程人為地轉化成若干“小步走”，這往往能使課堂顯得非常緊湊、熱鬧、好看，學生也因為“小步走”而覺得數學不難，生活不難。然而同樣的知識，當教師以更接近現實情況的數學問題考查學生時，就會發現原來課堂上的“高歌猛進”只是虛假繁榮。這正是因為學生平時“圈養”得過多，完整經歷問題解決的過程少，全歷程的數學活動體驗少，在解決實際問題過程中的碰壁、調整、反思、重建的過程不明顯造成的。為了使教學能夠突破這種“圈養”，筆者改進了教學設計。

三、第二次教學設計：“散養”探索

1.引出問題

教師出示例題：媽媽買雞蛋用去7.98元，每千克4.2元，媽媽買了多少千克雞蛋？要求學生說明“媽媽買了多少千克雞蛋”怎樣列式以及自己是怎樣想的。過程如下。

教師板書關系式：總價÷單價=數量

師：估算一下，這道題的商大約是多少？

生：把7.98看成8，4.2看成4，商大約是2。

2.探究算法

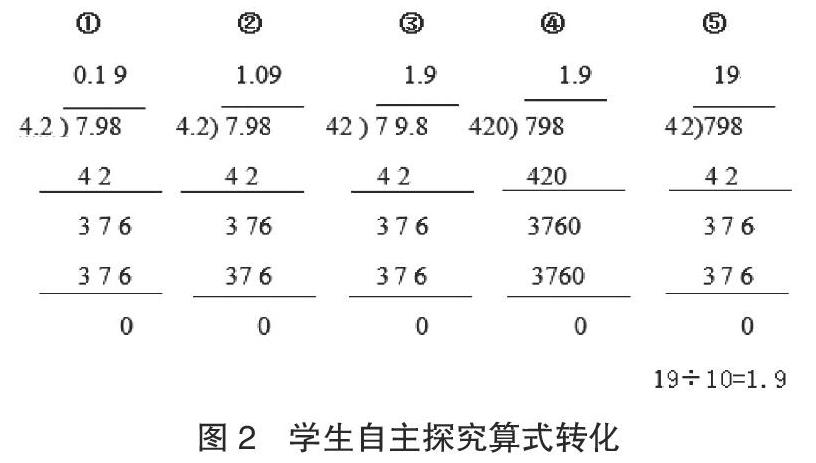
一是自主探究“7.98÷4.2”。教師給出研究提示：用以前學過的知識在學習單上算出來，并在小組內交流自己的想法。嘗試計算并展示不同的解法，說一說每種算法的思路是什么（見圖2）。

二是全班交流。請學生判斷：哪些算法是錯誤的？為什么？學生A說：估算的時候大約是2，所以不可能是0.19和1.09。學生B說：第一種7.98大于4.2，商應該大于1。學生C說：4.2×（）=7.98，商一定是一個一位小數，不可能是1.09。接下來是請計算正確的學生介紹經驗，說一說自己的算法思路。以下是學生的幾種回答。

（1）把除數和被除數同時乘10變成79.8÷42計算，或者把7.98元和4.2元換算成“角”計算（79.8角和42角）。

（2）把除數和被除數同時乘100變成798÷420計算，或者把7.98元和4.2元換算成“分”計算（798分和420分）。

（3）把除數乘10，被除數乘100，最后的商再除以10變成1.9。

三是理性思考。教師引導學生：先回味每一種算法，再靜靜思考，你比較欣賞哪一種算法，為什么？必要時可以舉例說明你的觀點。這里是希望通過學生之間的互動與交鋒，使爭論的話題聚焦在小數點移動的位數。如果學生觸及不到這一話題，教師可以提問：是不是一定要把除數、被除數全部轉化成整數？舉例說明。這樣，學生的舉例中必定會有類似于“2.916÷1.2”這樣的算式，這會讓學生進一步在豎式計算中體驗“移動小數點取決于除數的簡便性”。

四是比較抽象算法。請學生根據剛才幾道題目的計算，談一談它們在算法上有什么共同點。學生提出：都是把除數轉化成整數。教師完成板書“除數是小數→除數是整數”。

四、分析第二次教學中的“散養”

以上兩次教學中，教學二基本保留了教學一的優點，同時較好地解決了教學一中的不足，隱約可見“散養”的意味。具體體現在以下幾個方面。

1.放手創設大空間讓學生自主嘗試

突破“圈養”的明顯標志就是要給學生足夠大而可行的活動區域。因為學生已有“除數是整數的小數除法”的計算經驗，因此在教學二的開始，教師開門見山，比教學一少了兩個情境，這樣便于學生在黃金時間內集中精力解決主要問題。教學二通過減少兩個情境而拆除了不必要的框框，即沒有了教學一中過度的預設，使學生能直面更真實的問題，因而學生可以信馬由韁，使解決問題的過程更加完整，學習也更具連貫性。

2.突出了個體自主建構的全過程

長期以來，受傳統教學觀念的影響，課堂更多呈現的是“全體”——基于集體的教學，因而往往求同明顯，求異不足。個別化、個性化學習容易被忽視。教學二基于“散養”的理念，為突破以上局限做了一定的嘗試和努力。在課堂開始的自主嘗試環節，顯然每一個學生都在積極回憶、聯結、調取相關知識經驗，在積極地解決問題。無論嘗試正確還是錯誤，對學生個體來說都是一次有意義的經歷。在全班分享匯報環節，學生個體之間相互推動、相互啟發、相互學習，是促進每一個體實現不會到會、不明晰到明晰、不透徹到透徹的過程。在理性思考算法擇優環節，鞏固前面習得的計算方法，同時通過計算正確的學生舉例、計算，讓計算錯誤的學生體驗到小數點移動的關鍵點。最后通過抽象概括出“除數是小數的計算方法”。教師希望通過這種有目的的課堂“散養”，讓學生之間互相影響和推動，完成知識的自主建構。這樣，學生在教學中就不僅獲得了知識與技能，還有思想方法、過程體驗和經驗積累。

3.凸顯理性思維與學習探究的主動性

數學思維說到底是一種理性思維。雖然對小學生來說，強調理性思維還為時過早，但可以結合具體學習內容滲透理性意識。如本例中，在探究算法環節的理性思考部分，教師提出“先回味每一種算法，再靜靜思考，你比較欣賞哪一種算法，為什么”的問題，顯然就是想激發個體理性思考的意識。有的學生拘泥于自己的算法，有的學生聽過同伴發言后進行了調整或吸納了別人的算法，有的學生敏銳地發現了轉化中的簡便方法……接下來教師就以學生的有機生成（學生舉例的算式）作為學習資源，進行二次豎式計算，這一過程對大部分學生來說是驗證環節，對少數暫時有困難的學生來說是體驗過程，通過計算類似于“2.916÷1.2”的算式，體驗轉化中的簡便方法。這樣，就在學生主動探究的學習中體現了理性思維。

必須指出，這里的“散養”不是自由放養，而是一種積極而富有意義的、基于明確目的的“散養”，但是這種所謂的“明確目的”是隱性的，它隱藏于數學活動之中。教師的作用應該集中體現在教學活動的預見、設計和組織，即學習場的創建和維護上，使每一名學生在這樣的學習場中能夠自主選擇、自由奔跑、總結和反思，最大限度地突出“每一個的學習、每一個的生長”，而對學生核心素養的培育自然隱于其中。

參考文獻

[1]陳洪杰.追問觀點背后的觀點·小學數學教師[M].上海：上海教育出版社，2017.

（責任編輯? ?郭向和）