基于磁熱耦合仿真的筒式永磁調速器散熱研究

郭蘭中，姚騰，李新勇，彭劉陽

(1. 常熟理工學院 機械工程學院，江蘇 常熟 215000； 2. 中國礦業大學 機電工程學院，江蘇 徐州 221000)

0 引言

永磁調速技術是一種調速節能新技術，相比于液力耦合和變頻調速，永磁調速器具有軟啟動、不產生諧波污染等顯著優點，成為風機、水泵等離心式負載節能改造的首選[1-2]。

方軍、THOMAS、ALDO Canova等人對永磁調速器結構和材料性能參數對輸出轉矩的影響進行了仿真研究[3-5]；任慶等人利用二維有限元模型對渦流場和溫度場進行了仿真分析[6]；徐偉、王旭等人利用三維瞬態模型對渦流場進行了仿真分析[7-8]。

國內外對永磁調速器的研究很少涉及散熱方面，本文利用磁熱耦合有限元模型對永磁調速器關鍵零部件的溫度場進行了仿真分析，并對其散熱結構進行了優化仿真分析。

1 結構與致熱原理

1—散熱片；2—銅環基體；3—銅環；4—氣隙；5—永磁塊；6—永磁塊軛鐵。圖1 筒式永磁調速器結構圖

筒式永磁調速器結構如圖1所示。散熱片、銅環基體、銅環組成導磁轉子，固定連接到電機上，永磁塊、永磁塊軛鐵組成永磁轉子，固定連接到負載軸上。

工作時，電機帶動導磁轉子同速旋轉，銅環不斷切割永磁體產生永磁場，由于電磁感應現象，會在銅環中持續產生渦電流。當導磁轉子和永磁轉子之間的轉速差增大時，銅環切割磁感線的頻率加快，渦電流變大；當兩轉子嚙合面積增大時，銅環切割磁感線的數量增多，渦電流也會變大。

感應產生的渦電流使銅環中產生大量熱量，溫度不斷升高。這些熱量還通過熱傳導、熱對流方式向永磁調速器永磁體等部位傳遞，使其溫度不斷升高。當永磁體溫度超過其臨界工作溫度時，其磁性能會明顯下降。

本文對筒式永磁調速器兩轉子完全嚙合、轉差600r/min這一發熱量較高的運行工況進行研究。通過磁熱耦合仿真對其渦流場、溫度場進行分析，并通過對散熱片結構參量進行優化仿真，使永磁體溫度降到其臨界工作溫度以下。

2 磁場研究

永磁調速器銅環中的熱量是由磁場感應生成的渦流所產生，所以，要對永磁調速器銅環中熱源的發熱量和分布情況進行研究，就必須對產生渦流的磁場進行研究。

2.1 磁場仿真理論基礎

對磁場的有限元分析都是基于Maxwell方程組，本文研究低頻磁場，可忽略電流的位移效應，Maxwell方程組可表示為[9]：

(1)

式中：H為磁場強度(A/m)；J為渦電流密度(A/m2)；E為電場強度(V/m)；B為磁感應強度(T)。

銅環中的總電流密度可表示為：

J=Je+Jv

(2)

(3)

Jv=σv×B

(4)

式中：Je為變化磁場產生的電流密度；Jv為速度電流密度矢量；σ為電導率(S/m)；v為運動銅環速度(m/s)；A為矢量磁勢；t為時間(s)。

根據式(1)-式(4)，可求出電流密度J和磁感應強度B。

2.2 磁場有限元仿真

1) 前處理

磁場建模時，模型各部件尺寸如表1所示，其散熱片數量為40個。

表1 磁場、溫度場仿真模型各部件尺寸 單位：mm

各部件材料屬性如表2所示。

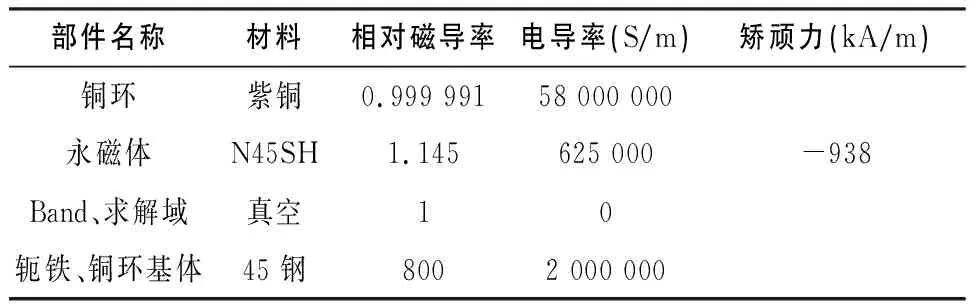
表2 磁場仿真各部件材料屬性

Maxwell磁場仿真采用自適應網格剖分技術，并對銅環、永磁體進行網格加密處理。

求解采用瞬態方法，設置總求解時長為0.09s，分為30個時間步，每步求解時長為0.003s。

2) 磁場仿真結果分析

從圖2可以看出，電流呈現渦旋狀，且相鄰兩個渦電流矢量在相鄰處疊加，使相鄰處的渦電流值相對于渦旋中心處較高。渦電流的最大值達到7.08×107A/m2，這些渦電流產生的熱量即為溫度場分析的直接熱量來源。

圖2 銅環中電流密度幅值和矢量分布云圖

3 磁熱耦合研究

本文研究的永磁調速器永磁體采用N45H釹鐵硼材料，其最高工作溫度為120℃，在此工作溫度以下，其磁性能相對穩定，所以本文采用磁熱單向耦合的方法。

3.1 溫度場理論基礎

永磁調速器中銅環是直接發熱源，其產生的熱量通過熱傳導向銅環基體和散熱片等部件傳遞，熱傳導的基本方程為：

Q=λAΔt

(5)

式中：Q為傳導的總熱量(J)；λ為導熱系數(J/(m2·℃))；A為接觸面積(m2)；Δt為溫差(℃)。

熱傳導微分方程形式為：

(6)

散熱片外表面、永磁轉子內表面和各部件端面在運轉過程中攪動周圍空氣，與空氣進行強制對流作用，將熱量散發出去，對流換熱的基本方程為：

Q1=h(Tw-Tf)

(7)

式中：Q1為對流交換的總熱量(J)；h為對流換熱系數(J/℃)；Tw為散熱片表面溫度(℃)；Tf為周圍空氣溫度(℃)。

其微分方程形式為：

(8)

式中：λx、λy、λz分別為求解域內x、y、z3個方向的導熱系數；T為求解域內各點溫度(℃)；qv為發熱源的熱流密度(W/m2)。

散熱片外表面或永磁轉子內表面對流散熱系數可用下式求得：

(9)

式中：v為導磁轉子外圓周面或永磁轉子內圓周面線速度(m/s)；R為導磁轉子外徑或永磁轉子內徑(m)；n為導磁轉子或永磁轉子轉速(r/min)。

導磁轉子端面散熱系數為：

(10)

永磁轉子端面散熱系數為：

(11)

式(10)-式(11)中：Re1、Re2分別為導磁轉子和永磁轉子端部氣流雷諾數；n1、n2分別為兩轉子轉速(r/min)；Nu1、Nu2分別為兩轉子端部努塞爾特常數；λa為空氣的導熱系數(W/(m·K))[10]；μ為空氣運動黏度系數(m2/s)。

3.2 磁熱耦合有限元仿真

1) 前處理

本文利用ANSYS Maxwell 3D模塊和Steady-state Thermal模塊進行耦合仿真，在Workbench中建立的關系圖如圖3所示，即將磁場仿真結果文件中的熱生成導入到溫度場分析的初始化設置中。

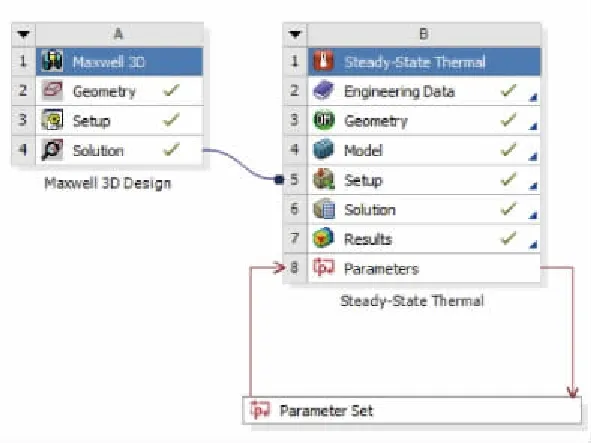
圖3 磁熱耦合仿真連接關系圖

溫度場分析的三維模型和磁場大致相同，需再建立一個兩轉子之間的氣隙區域。散熱片采用Workbench自帶的模塊DM進行重新建模，便于對散熱片的底板厚度、肋片厚度、肋片高度、肋片數量這幾個參量進行參數化設置。

使用控制變量法，設置散熱片底板厚度h1在1.7mm～2.2mm變化，肋片高度h2在5mm～11mm變化，肋片厚度h3在1.4mm～2.6mm變化，肋片數量在37～42范圍內變化，并對銅環溫度、永磁體溫度兩個參量進行輸出參數化設置。

溫度場仿真中各部件材料屬性如表3所示，其中兩轉子之間的空氣區域流動狀態較為穩定，可將其熱量傳遞方式等效為熱傳導，直接賦予空氣的導熱系數值。

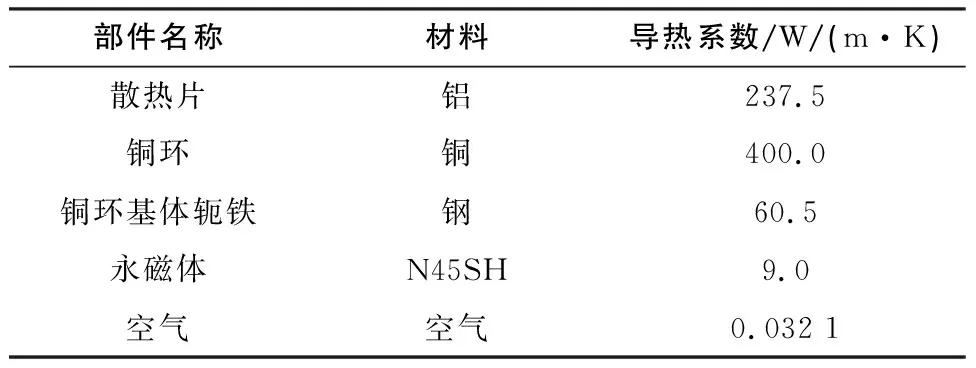
表3 溫度場仿真各部件材料屬性

溫度場仿真中，筒體部件采用面網格進行剖分，其他部件指定最大單元尺寸進行剖分。

溫度場仿真中分別對散熱片外表面、永磁轉子內表面以及兩轉子端面施加熱對流載荷，其對流散熱系數值按照式(9)-式(11)進行計算，并設置環境溫度為22℃。

磁場仿真計算得到的渦流熱以熱生成率(W/m3)的形式施加到溫度場仿真模型銅環部件中，其熱生成率云圖如圖4所示，在軸向上呈現中間高、兩端低的趨勢，且銅環內表面的熱生成率高于外表面。

圖4 銅環熱生成率云圖

前處理設置完成，就可以開始求解，求解完成即可通過后處理得到銅環和永磁體上的溫度分布情況以及散熱片采用不同結構參數組合情況下的銅環和永磁體的最高溫度。

2) 仿真結果分析

從銅環和永磁體溫度分布云圖(圖5)可以看出，當永磁調速器溫度達到穩定狀態時，銅環上的溫度呈現中間高兩端低的趨勢，且內表面溫度略大于外表面，永磁體靠近銅環的一側溫度高于其內表面的溫度，銅環和永磁體最高溫度分別達到248.79℃和122.06℃。

根據散熱片結構參數優化仿真結果數據，分別繪制銅環、永磁體最高溫度與散熱片肋片高度、肋片厚度、底板厚度、肋片數量的關系曲線，如圖6-圖9所示。

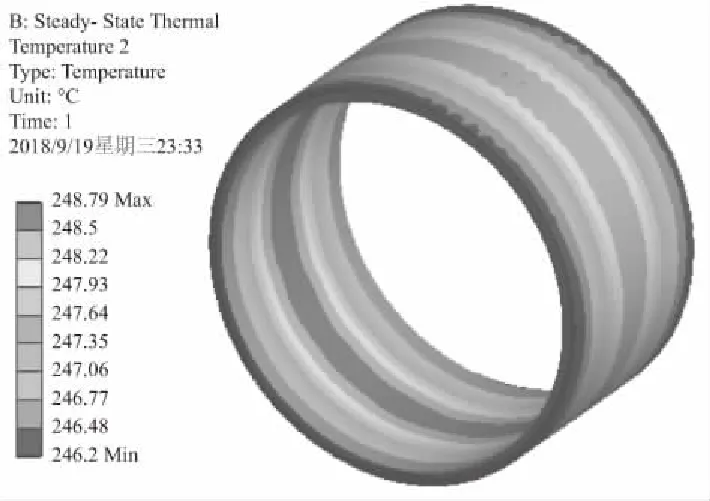
圖5 銅環和永磁體溫度分布云圖

圖6 散熱片肋片高度優化結果曲線

圖7 散熱片肋片厚度優化結果曲線

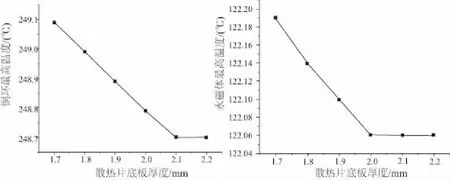
圖8 散熱片底板厚度優化結果曲線

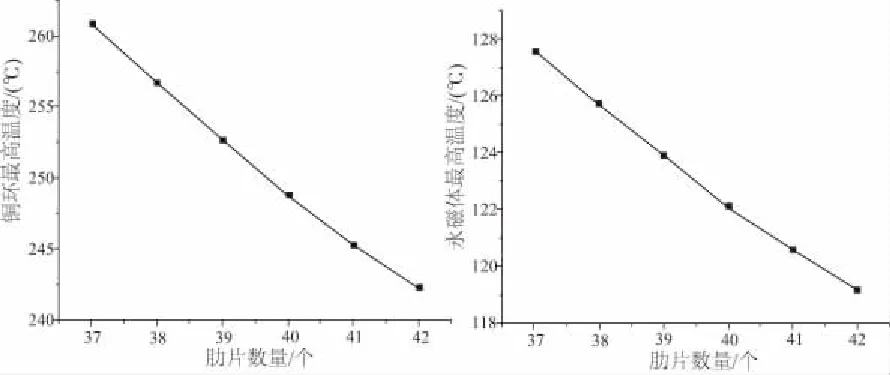
圖9 散熱片肋片數量優化結果曲線

根據仿真結果曲線，在保證散熱片結構機械強度的前提下，適量地增加散熱片肋片高度、肋片厚度以及肋片數量都可以顯著降低銅環和永磁體最高溫度；而適當增加底板厚度可以降低銅環和永磁體的最高溫度，但降低幅度較小。

4 結語

1) 永磁調速器運行時，會在銅環中持續產生渦旋狀電流，這些渦電流產生的熱量即為永磁調速器的發熱熱源。

2) 永磁調速器銅環上的溫度呈現中間高兩端低的趨勢，且內表面溫度略大于外表面，永磁體靠近銅環的一側溫度高于其內表面的溫度。

3) 根據永磁調速器散熱片仿真優化結果，合理選擇肋片高度、肋片厚度、肋片數量的數值，可以顯著降低永磁調速器各部件溫度，這為散熱片的結構優化提供了參考。