直升機旋翼電加熱組件高頻熱載疲勞試驗研究

洪程，高長水，劉壯

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引言

我國幅員遼闊，氣候復雜多樣，存在較多結冰易發區，直升機旋翼槳葉防除冰技術的需求日益迫切，國內外都積極開展了電熱防除冰技術的研究工作。數十年來，國內外對直升機旋翼槳葉電加熱組件的疲勞強度問題已經進行了大量的探索，但是仍然只掌握了小部分直升機旋翼電加熱組件疲勞破壞的規律。劉達經[1]等對直升機旋翼槳葉電加熱系統中電加熱組件疲勞及結構的相容性等關鍵技術進行了相應的研究；劉正江、顧寒[2]對直升機旋翼槳葉防除冰表面碳纖維加熱組件的溫熱特性進行了試驗研究；DEAN Nguyen[3]等針對黑鷹直升機UH-60直升機旋翼槳葉新型電加熱組件疲勞壽命進行了簡單的測試。

1 地面疲勞試驗系統原理

地面疲勞試驗系統是針對直升機旋翼槳葉電加熱組件的疲勞壽命進行測試的系統，電加熱組件粘貼在模擬件上、下兩表面相同位置。系統主要由兩個子系統構成：一是加熱及溫度控制系統，二是振動試驗系統。設計整個試驗系統的原理，如圖1所示。

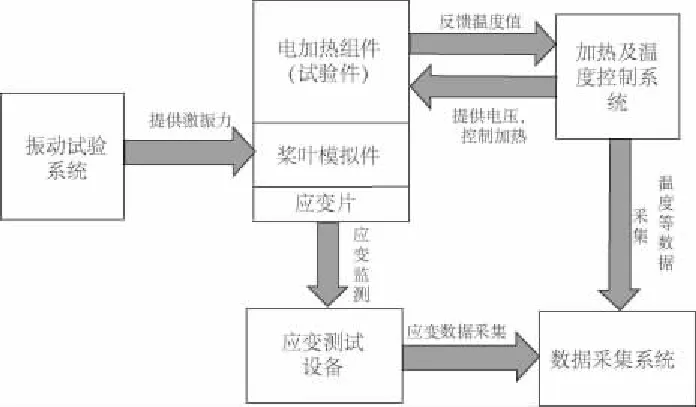
圖1 地面疲勞試驗系統原理圖

電加熱組件內部布置有加熱電阻與溫度傳感器，并利用溫度傳感器與溫控表讀取電加熱組件內部與表面的溫度值，該值與加熱及溫度控制系統中預設溫度上、下限進行比較，若測得溫度低于下限值，則系統開始加熱；若測得值高于溫度上限值，則系統停止加熱，從而實現溫度控制。在加熱過程中，電加熱組件粘貼于模擬件表面，振動試驗系統為模擬件提供激振源，在合理的槳葉工況模擬方案下，使模擬件按照特定規律帶動電加熱組件振動，從而在模擬件表面產生試驗所需的應變。模擬件表面粘貼有應變片，通過應變測試設備實時測量試驗過程中模擬件表面應變值。數據采集系統將應變測試設備測得的模擬件表面應變值以及電加熱組件疲勞壽命、加熱循環次數等關鍵參數記錄保存。

2 疲勞試驗方法研究

振動會使物體產生疲勞破壞，疲勞破壞是物體的往復運動在其局部產生裂紋而最終物體斷裂的過程，而且由物體本身共振所導致的疲勞會使物體結構疲勞周期減少，加快了對結構的破壞。因此為縮短試驗周期，試驗可選用共振法。直升機槳葉電加熱組件在其壽命周期內可以承受數百萬應變循環，所以在對振動試驗系統槳葉工況模擬時應該盡可能選用模擬件固有頻率高的工況，固有頻率越高，模擬件在短時間內可以承受更多的應變循環，試驗系統可以實現對電加熱組件疲勞壽命快速測試。

采用文獻[4]中直升機旋翼槳葉疲勞試驗系統的模態分析結果(表1)，其仿真計算結果表明前4階振動的主要振動形式以揮舞耦合擺振為主，更高階的情況在后面的試驗系統中無需考慮，這是因為直升機在正常飛行過程中這種高頻率的情況是不會出現的。

表1 系統模態表

3 槳葉工況模擬方案

地面振動試驗的目的是對槳葉內電加熱組件在大應變條件下，進行快速測試，故需設計合理的槳葉工況模擬方案，使電加熱組件在試驗時承受一定要求的振動載荷。

試驗系統槳葉工況模擬方案如圖2，由模擬件及相應的夾具組成。夾具夾持在模擬件中間位置(確保激振位置處于模擬件中間)，且夾具通過螺栓連接方式與振動臺臺面相連。這種方案使用的是“自由-自由”模式[3]，激振源頻率采用模擬件的1階固有頻率。

圖2 試驗系統

振動臺按照振動譜設定規律進行掃頻振動，測得模擬件1階固有頻率為31.3Hz。由表1可知，直升機槳葉1階固有頻率為6.1Hz，2階固有頻率為18.9Hz，且直升機在實際工作時其槳葉振動頻率一般不會超過其2階固有頻率，故該方案可以實現在更短的時間內將電加熱組件破壞，實現對電加熱組件疲勞壽命的快速測試。

4 動圈加速度a對模擬件表面應變的影響

4.1 應變與加速度理論關系

由牛頓第二定律可知，受力物體會獲得加速度，除了加速度外，應變也是物體受力的體現，即在物體加速運動情況下，物體結構一定會產生應變。應變與加速度之間的關系如下[5]：

(1)

ΔF=Δm·a=ΔV·ρ

(2)

由式(1)、式(2)可得：

(3)

式中：σ為模擬件振動時產生的應力；E為物體材料彈性模量；ε物體表面的微應變；Δm則是微元模塊的質量；a是物體運動時的交變加速度；ΔS是微元模塊的表面面積；ρ是材料密度；Δh是微元模塊高度。其中彈性模量、材料密度均為常數，故加速度與應變存在正比關系：

ε=ka

(4)

4.2 k值分析

槳葉模擬工況方案選定后，還需對模擬件再進行瞬態分析，給定不同的位移幅值從而給模擬件加載不同的加速度。不同加速度情況下模擬件表面中間位置應變通過仿真計算得到如表2所示結果。

表2 仿真加速度與模擬件表面應變關系

從表2數據結合式(4)還可以發現，模擬件表面應變與加速度關系如式(5)：

ε=(1 510～1 562)a

(5)

在已設計完成的振動試驗系統中，對試驗件表面中間位置應變進行實際測量，測量結果如表3所示。

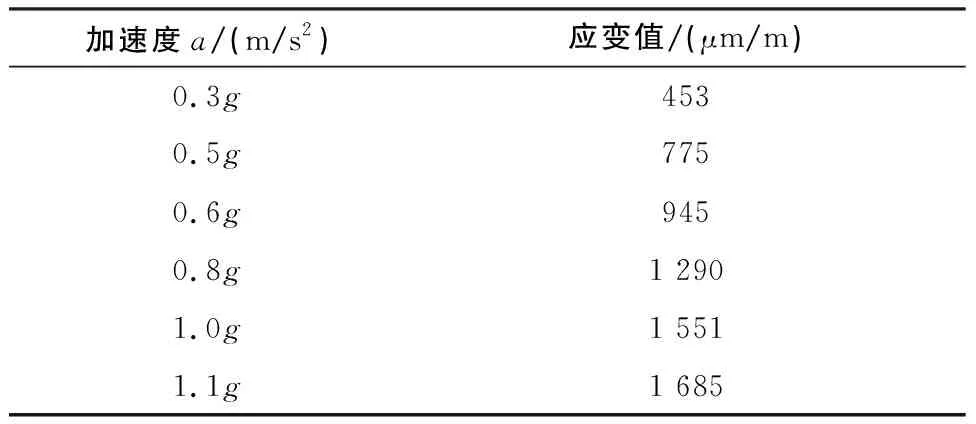
表3 實測加速度與模擬件表面應變關系

結合式(3)與以上數據結果繪制應變-加速度規律如圖3所示。

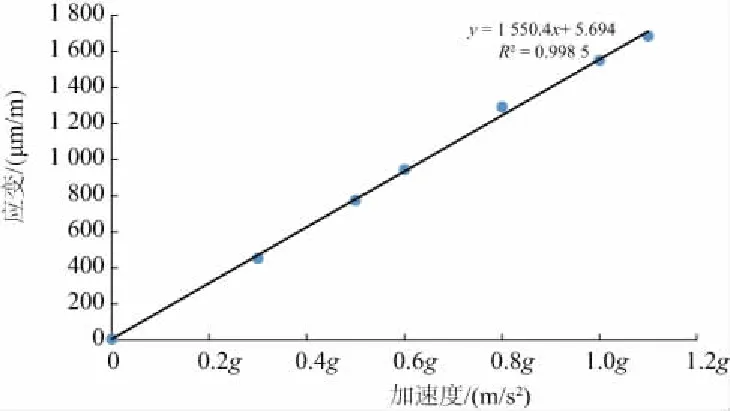
圖3 應變-加速度關系圖

圖3中直線為根據試驗數據所得點繪制的線性回歸曲線，該直線在理論上來說是應該過原點的，分析其未過原點原因有如下兩種：

1) 應變片在振動過程中出現松動，初始狀態改變；

2) 測量儀器的測量誤差，儀器在測試過程中受到一定干擾，導致工作時0值會發生偏移。

克服方法如下：

① 嚴格按照應變片粘貼流程將其粘貼到模擬件表面，多次調試，若不合要求重新粘貼；

② 定期查看應變測量儀器，若有偏差，及時進行0值校準。

圖3中線性回歸公式如下：

ε=1 550.4a+5.694

(6)

式中：ε為應變值；a為加速度。

試驗結果方差分析如表4所示。表中df表示自由度，SS表示平方和，它所在列的3個數值分別為回歸誤差平方和、殘差平方和及總體平方和，MS表示SS和df的比值，F是顯著性檢驗值，S表示模型為假的概率及“棄真率”。

表4 試驗結果方差分析表

對此回歸模型進行顯著性檢驗，從方差分析表4中可以得到檢驗值F=1462.663。查閱F檢驗的臨界值表可以得出，在f回=1、f剩=4以及置信區間為0.05的情況下，F的臨界值為8.59[6]，很明顯小于得到的F值，檢驗結果表明該回歸方程同樣是顯著有效的。同時通過回歸分析得到的擬合優度R2=99.72%，此數據表明該模型的擬合程度很高。

將式(6)與式(1)對比，試驗所得直線斜率在仿真計算斜率范圍內。

按照曲線公式，將加速度a值從0.3g～1.1g分別帶入式(6)，應變計算值與實際值如表5。

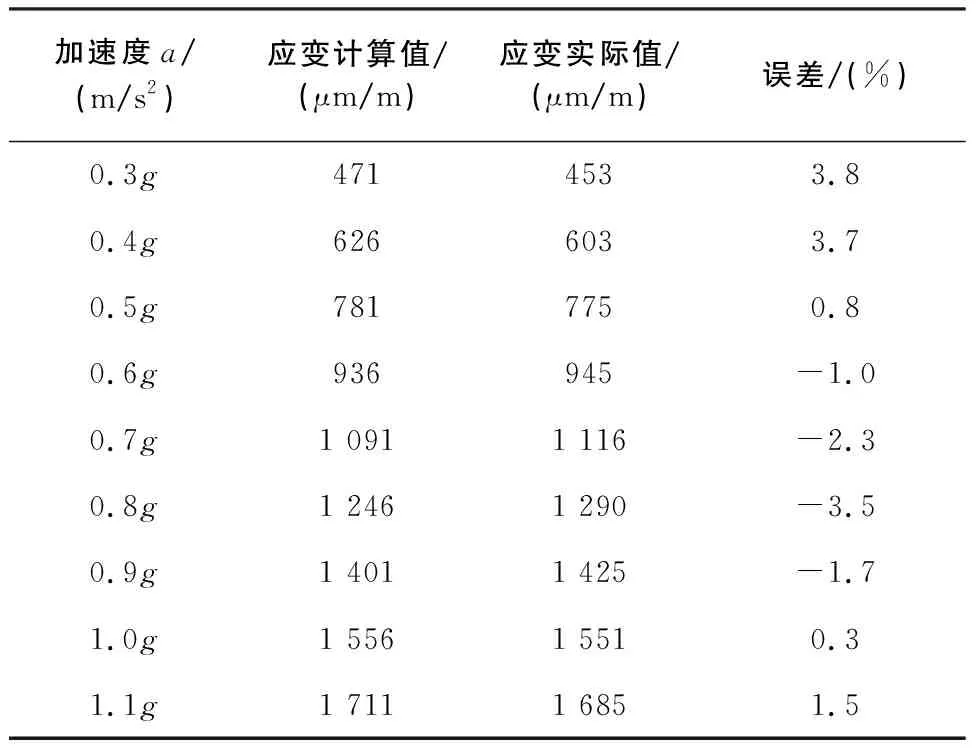
表5 應變計算值與實際值

從表5可知，根據公式計算的結果與實際測得結果誤差<5%，故在試驗系統中，可以通過該公式進行應變調節。

5 結語

通過實際試驗測試，確定了合理的疲勞試驗方法與槳葉工況模擬方案。同時為使試驗系統適用于不同動載荷環境的電加熱組件的疲勞壽命測試，通過仿真與實驗得出了模擬件表面應變與振動臺振動量級的函數關系，對地面疲勞試驗系統的廣泛使用有實際意義。