第三屆國際數學教材研究與發展會議綜述

綦春霞，曹 辰，付 鈺

第三屆國際數學教材研究與發展會議綜述

綦春霞，曹 辰，付 鈺

（北京師范大學，北京 100875）

2019年第三屆國際數學教材研究與發展會議主要包括教材的研究理論、教材的開發、教材內容的呈現方式、教材的發展、教材的比較、數字教材等主題．通過對會議論文及會議發言的梳理，可以歸納出國際數學教材研究的最新觀點、成果與方向，并為中國數學教材研究提供一定的借鑒．

教材內容呈現；教材比較；教材歷史；數字教材

繼第一屆在英國、第二屆在巴西，第三屆國際數學教材研究與發展會議于2019年9月16—19日在德國帕德博恩召開，來自美國、英國、德國、中國、日本、韓國、新加坡、巴西、法國、南非、以色列、瑞典等18個國家的一百九十多位專家出席了會議．按照大會議程，第四屆國際數學教材大會將于2021年在北京師范大學召開．為了更好地借鑒國際經驗，提升中國數學教材研究的水平，這里試圖對第三次國際數學教材會議的內容進行介紹，以期對中國的數學教材研究提供一定的借鑒．

此次會議共包括4場大會報告、４場專題討論會以及兩場工作坊和多場小組會議研討，主要涉及數學教材的分析與評價、數學教材的內容分析、數學教材的比較、數學教材的使用、數學教材的開發、信息技術和電子平臺6個方面．

1 基于理論的數學教材分析與評價

關于教材分析與評價的研究是此次會議的重要議題，德國萊布尼茨科學和數學教育研究所的Henning Sievert等學者發現，教材質量對于學生的學業成績有顯著影響．此次會議著重關注從理論角度去分析和評價教材，是數學教材研究的最新方向．

1.1 教學認識論

在此次會議中，多國學者利用人類行為學中的“ATD（anthropological theory of didactics）”模型[1]，展示了他們在教材評價上的成果．日本鳴門教育大學的Toru Hayata與Sakura Amor學者對日本一~六年級幾何教材中所提出的問題進行了分析，以研究這些問題是否可以支持學生幾何思維的發展．其結果發現，一~五年級教材中設置的問題可以支持學生幾何思維的發展，而六年級教材中則存在一定問題，因為其關于圖形性質、變換、數學活動的問題數量明顯減少．據此提出建議，在六年級教學中，教師需要對教學方法進行適當調整，或者教材需要重新設計．挪威科技大學的Solomon A. Tesfamicael等學者對于挪威教材中多種函數概念表征間的轉換方式進行了分析．結果發現，大部分表征方式之間的轉換過程符合ATD理論，可以有效幫助學生加深對函數概念的理解，但也存在一些轉換過程不符合ATD理論．基于以上發現，他們建議可以基于ATD理論，對教材內容進行標定并修正，以提高教材的使用效果．而德國帕德博恩大學的Tobias Mai與Rolf Biehler應用以上理論，對3本德國教材中向量概念的引入方式進行了比較研究．研究表明，每本教材對向量的引入方式均有所不同，有些側重于從代數角度進行引入，有些則從幾何的角度．而德國錫根大學的Frederik Dilling對以上問題進了進一步探索，他發現幾何方法在數學和物理教材中占主導地位．進而提出，為了讓學生全面理解向量概念，應將概念的不同方面都呈現給學生，向量在數學和物理課中的應用應協調一致，這樣學生就不會在單一學科中形成片面的向量概念．具體地，物理課應強調矢量的代數表示，數學課應強調矢量的物理應用．教師不僅要學習教學的基礎知識，而且要學習其它學科的基礎知識，并在學科交流中發現共性．

1.2 語言符號學

多特蒙德理工大學的Jennifer Dr?se與G?tze Daniela利用語言學和符號學理論，對教材內容進行了細致地研究．Jennifer Dr?se對德國四年級（小學）、五年級（初中）數學教材中的應用題表述進行了比較研究．她發現，相比于四年級教材，五年級教材應用題中的動詞、名詞明顯增多，導致其語言理解難度與問題情境的復雜度明顯增加．為了幫助學生適應小學、初中的銜接，她建議，五年級教師需要重視對于教學內容的準備與編排，以幫助學生盡快適應五年級教材的表述特點．而G?tze Daniela利用語言學中意義相關的詞匯對教材中圖像、文字、符號之間的關系進行了優化，形成新的實驗教材，并記錄了一位四年級學生使用以上教材的學習過程．研究表明，在學習過程中，意義相關的詞匯具有中介作用，可以將具體的或標志性的表征與運算聯系起來，從而有助于學生理解．

日本筑波大學的Shogo Murata使用四邊形層次分類法[2]（de Villiers，1994）的5個維度對兩套日本最新中學教材中的幾何部分進行了分析．研究表明，以上教材中并沒有包含四邊形層次分類的所有維度，他建議教材中同一概念需要有多種定義方式，即只從一個維度呈現概念是不恰當的．

1.3 多元表征理論

華東師范大學鮑建生研究團隊從ERIC和CNKI上共收集了211篇關于數學表征的文獻，發現僅19篇文獻是關于數學教材中數學表征的研究．這些文獻主要以中小學教材為研究對象，研究關注某一教材的數學表征特點，或者對多本教材的數學表征方式進行比較，研究內容聚焦算術、代數和幾何，主要采用文獻分析法或比較研究法進行研究．鮑建生認為，隨著數字教材和其它形式教材的不斷出現，需要加強對教材中數學表征的研究以適應時代的進步，但目前關于數學教材表征的研究還處于起步階段，研究方法和工具相對簡單．

西班牙巴斯克大學的Oihana Moreno-Arotzena等學者借助Hughes Hallett等學者提出的“四法則”理論[3]，即概念可以用圖像、數字、符號、文字4個角度進行表征，以大學數學教材中的“梯度”概念為例，分析教材中是否均存在相應的任務以幫助學生完成“梯度”概念不同表征之間的轉換，從而對教材的質量進行評價．類似地，德國弗里德里希-亞歷山大大學埃朗根-紐倫堡分校的Jennifer Postupa提出，可以通過比較教材中圖表、注釋及任務的數量，以比較不同年代、不同國家數學教材的編寫特點．

荷蘭Marc van Zantenl與Marja van den Heuvel-Panhuizen學者為發現“現實數學教育”這一思想是如何影響荷蘭數學教材的編寫，對荷蘭一~三年級教材中的加減法內容進行了分析．研究發現，在近些年的教材中，關于闡釋加減法運算過程的直觀表示越來越具體，這影響了學生對運算的多樣化理解，因為學生動手嘗試所帶來的實踐性與開放性是難以被取代的．據此建議，教材在編寫過程中應適度“留白”．

2 教材內容的評價

此次會議中，基于教材內容的評價研究是重要議題之一．多位學者在教材內容呈現方式、編排順序以及研究方法上展示了他們的研究成果．

2.1 內容的呈現方式

學者Allan Tarp以小學數學教材為研究對象進行教材內容的評價研究，他認為：當單詞語言作為對外部世界的描述對學生進行外部教授時，數字語言作為其元語言或語法的例證而在內部教授，這使得數字語言更加抽象，難以學習和應用．因此建議：數學教材應進一步引導孩子們掌握“許多”這個概念知識，因為“許多”這個概念涉及比例、微積分、方程和建模等數學核心知識．

巴西Cydara Cavedon Ripoll等學者針對分數的性質、分數運算兩部分內容對巴西小學教材進行了分析．研究發現，只在兩本巴西教材中明確提及分數相等的判別標準．隨著分數學習的深入（巴西六年級），分數等價性問題才能得以解決．

巴西Lourdes M. Werle de Almeida等學者以高等數學教材《微積分第2卷》為研究對象，對教材如何引入二重積分概念的方式進行探究．結果表明，教材引入二重積分概念的方式是通過圖表推理呈現的，學生在使用教材的過程中用圖表表征自己的認知過程，有利于加深他們對概念的理解過程．

墨西哥Josip Slisko等學者從宏觀角度對數學教材中的不合理編排和錯誤的事實性知識進行了調查．調查結果表明，不清晰的問題和不必要的復雜作圖任務對學生的表現會產生負面影響．因此，Josip Slisko等學者建議，如果出版社和教育部的修訂程序無法解決墨西哥教材存在的以上問題，教師應設計“合理改變教學順序、引導學生發現并糾正作者使用的錯誤公式”等活動，以幫助學生減少其負面影響．

2.2 教材中的數學史

很多教材中出現了關于數學史的介紹．南安普敦大學的范良火與華東師范大學的李楠比較了上海教育出版社、人民教育出版社的兩套中小學數學教材中數學家是如何呈現的異同．研究表明，兩套教材均介紹了中國與國外的數學家，但是大多數介紹的數學家都是古代數學家，初中教材更加重視對數學家的介紹．但德國學者Sebastian Schorcht指出，大部分教師并沒有意識到數學史與數學知識、數學思想方法等的關聯，而是簡單地利用“數學史”內容提高學生的閱讀能力．

2.3 教材評價的方法

在傳統的教材評價工作中，往往需要對教材每一頁的內容進行詳盡分析，這需要極大的工作量．薩姆休斯頓州立大學Dustin L. Jones等學者為了提高分析效率，在參照原有結論基礎上，分別采用簡單隨機抽樣、系統抽樣、分層隨機抽樣、整群抽樣4種抽樣方法以調查統計內容在以上教材中的分布狀況，并將抽樣結果與全面調查的結果進行對比．研究發現，在以上的抽樣方法中，分層抽樣后的統計結果誤差最小，這將有利于進行大范圍的傳統教材評價工作．

3 教材的比較研究

在數學教材比較或歷史發展方面，國際會議學者不僅關注教材間的橫向比較研究，也專注了教材的縱向比較研究．

3.1 橫向比較研究

Yasin Memi?等學者對不同國家同一數學內容進行分析與研究．土耳其阿納多盧大學Yasin Memi?等學者探討了土耳其、新加坡和加拿大中學數學教材中比例推理的內容分布．結果表明，新加坡教材中比例推理內容所占比例最大，讓學生經歷較完整的體驗比例推理的學習過程，而加拿大和土耳其教材中比例推理內容所占比例較小．因此指出：研究結果為教材編寫者和課程決策者提供了重要的反饋．

巴西Franciele Marciane Meinerz等學者對巴西、西班牙與葡萄牙的多部數學教材中方程、不等式內容的呈現方式進行比較．研究發現，三國教材中均使用天平模型幫助學生理解方程概念，但在不等式內容中，天平模型僅作為引入內容．同時，三國數學教材均缺少“幫助學生理解方程與不等式內容之間的聯系”的相關數學內容的設置．因此建議，在教材開發中，天平模型不但可以幫助學生更好地理解方程與不等式的相關概念，還可以幫助學生認識此二者之間的聯系．

華東師范大學的陳月蘭和何曉燕對中國、日本、美國高中數學教材中的三角函數內容及編排特點進行了細致研究．研究表明：3個國家對三角函數的重視程度較高，但中國教材中三角函數的內容最少．在美國和中國的教材中，三角函數的應用設置在三角函數之后，而日本教材則相反．因此建議，單位圓應該作為三角函數學習的有效工具，教師可以利用單位圓的對稱性引導學生來探索三角函數公式．

3.2 縱向歷史研究

縱向比較主要集中于對不同時期的數學教材進行比較，以發現數學教材的明顯特征變化以及數學內容滲透的變化．華東師范大學鮑建生與Hyoungmi Cho著重分析了2009、2015年韓國小學數學教材中在分數除法、分數直觀表示上的異同．研究表明，隨著韓國數學課程的修訂，2015年教材的分數除法內容也強調了情感特征．2009年和2015年的教材都將分數除法分為不同類型的運算法則、概念化和直觀表示．2009年的教材打算在邏輯上和程序上提出“乘除法轉換法則”．另一方面，2015年的教材旨在激發學生對各種表示的興趣，如分數除法運算法則和直觀表示．

肯尼索州立大學的Tad Watanab對日本兩個版本教材中“比、比率和比例關系”內容進行縱向和橫向對比．研究表明，雖然比例關系的概念在四、五、六、七年級均有所涉及，但是在每個年級都不斷滲透新的數學知識與更高的數學學習要求．并且，日本課程明確區分了不同單位的兩個量與同一單位的兩個量間的比較問題，這兩種類型的比較均在五年級出現．但是在上一次修訂中，六年級出現了“單位1”的概念．因此，對該部分內容不同引入順序的比較在日本數學教育界似乎仍是一個懸而未決的問題．作者建議，擴大分析范圍可能會讓人們對教材中比例關系的處理有更多的認識．

4 數學教材使用研究

數學教材使用研究始終是數學教材研究領域的熱點話題．此次會議中，一些學者采用社會教學四面體（socio- didactical tetrahedron，簡稱SDT）理論[4]，對“學生、教師、資源”之間的互動關系進行了研究．SDT理論模型如圖1．

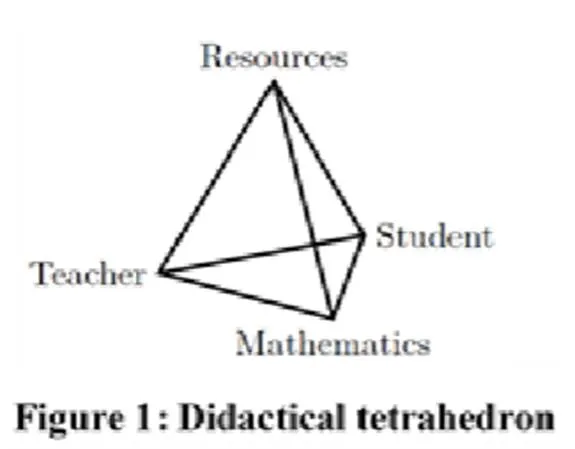
圖1 SDT理論模型

4.1 教師與教材的互動

薩格勒布大學的Dubravka Glasnovi? Gracin與奧西耶克大學的Ljerka Juki? Mati?對學生和教師使用教材的方式和原因進行了探究，并著重探討了影響教師與學生使用教材的社會性因素．從學生和教師兩個相互依存的角度進行個案研究，將教學和教材的使用描述為社會過程．結果表明，學生對教材的使用依賴于教師在學生和教材之間的中介調節過程．此外，許多教師關于教材使用的方式會受到教師的社會構成規范的影響．

4.2 學生與教材的互動

美國密歇根大學的Vilma Mesa等學者通過對教材內容進行編碼，以調查教師、學生在微積分、線性代數和抽象代數學習中使用數學教材的情況．結果表明，在教材的使用過程中，與其它教材相比，以數學學科能力為導向的數學教材更能促進學生的數學學科能力的提高．在學生學習例題與完成習題的同時，他們在數學思維方式、數學符號的使用、提出和解決數學問題方面有很大的提高．

5 數學教材開發研究

德國波茨坦大學的Thomas Jahnke認為，教材開發中應體現理論基礎、實踐基礎、教學實例與任務實例的融合．

5.1 教材開發的原則

多特蒙德工業大學的Susanne Prediger認為，教材的編寫應體現以下原則：（1）支持學生的理解過程；（2）通過合作促進概念理解；（3）引導學生實現“再創造”和“數學化”；（4）在“垂直數學化”中幫助學生進行知識主動建構；（5）在多元表征和不同數學方法間建立聯系．

5.2 教材開發的方法

作為丹麥一~九年級數學教材的編寫者，奧胡斯大學的Tomas H?jgaard認為，理論模型在教材開發上可以起到規劃教材的內容結構、確定每一章節的核心能力以及指導每章節內容的呈現方式的作用．在開發過程中，他提出了一個“年級—能力—概念”三維模型以規劃教材的頂層設計．在每個年級的教材編寫中，所有教學內容都會在這個模型中找到合適的位置（如圖2六年級教材所示），以便可以從適當的角度完成對該部分內容的編寫工作．六年級教材內容所體現的核心能力在框架中的分布如圖3所示．

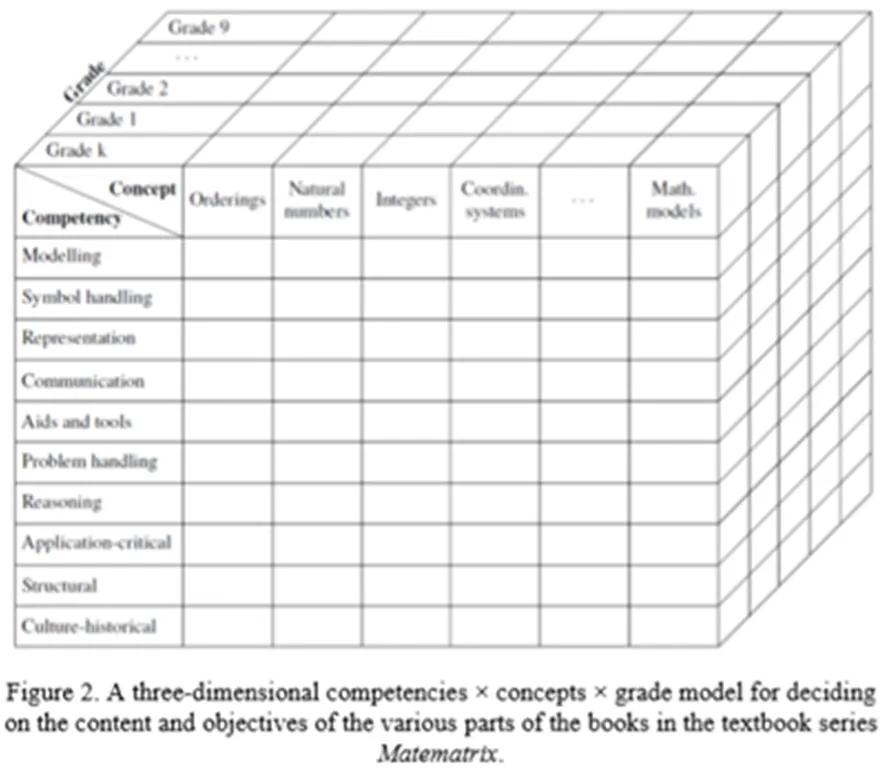
圖2 “年級—能力—概念”三維模型

圖3 六年級教材內容所體現的核心能力在框架中的分布

作為一種學習理念，“項目式學習”在近10年來被越來越多地應用到學科教育領域，北京師范大學的綦春霞在大會上作“基于項目式學習理論教材的開發與實踐”的報告．在理論研究方面，綦春霞團隊厘清了數學項目學習的實施標準及評價標準；歸納了當前國際數學教育領域新興的項目學習模式；明確了項目學習在數學學科中應用路徑、影響效應及面臨的挑戰等；規范了數學項目式課程設計的一般路徑，即確定核心概念、明確知識目標、預設知識的發展序列、確定項目主題及任務分割．在實踐研究方面，綦春霞團隊明確了數學項目式課程的功能定位、基本體例及設計原則等，為后續系統設計項目式課程提供統一規范；以《課標》和教材為參考，系統設計了初中項目式數學課程．研究發現，項目學習課程能夠適應初中生的認知風格和學習需求，對于學生數學問題解決、探索創新等能力，學習態度、興趣等非智力因素的培養有顯著的積極影響．

6 基于信息技術的學習工具

數字教材和智慧學習平臺也是此次大會的重點議題之一．荷蘭埃因霍溫理工大學的Birgit Pepin在報告中指出：數字教材可能有助于教育創新，因為它們可以幫助教師在教學過程中實現新的課程意圖．同時，數字教材也可能阻礙真正的創新，因為它們限制了教師重新課程設計與開發能力．他認為，除了培訓教師恰當地使用資源外，還應綜合培養教師的資源開發能力．

6.1 數字教材的開發

相比于傳統紙質教材，數字教材在改革課堂教學模式，研究學生學習特點上起到了突出的效果．通過觀察學生的行為、參與程度和與同伴的交流，利用數字教材可以判斷學生是否深度參與了課堂教學活動．在德國，第一批數字教材在過去的幾年里已經出版．隨著“資源”概念的拓展，產生了新的教材觀念，因此多樣化的數字教材也隨之發生了結構性的變化．因此德國杜伊斯堡-埃森大學的Maximilian Pohl與Florian Schacht認為，研究者既需要關注數字教材的結構變化，也需要關注學生對數字教材的實際使用情況．

根據美國學者Alden J. Edson, Elizabeth D. Phillips與Kristen Bieda的課堂實踐，他們發現在以探究為導向、以問題為基礎的數學課堂中，數字教材可以發揮重要的協作特性．首先，在和他人分享交流的過程中，學生可以經歷生成、評價、改進自己作業的過程，從而提高自己的表達能力；同時，通過理解他人的作業，可以加深對數學概念的理解．數字教材的協作特性增強了課堂上的社會互動能力，可以提高學生在數學情境中提出問題的能力，樹立數學學習自信心．

數字教材還為評價和分析學生在數學課堂中的參與程度提供了新的途徑，擁有很大的研究潛力．基于253名六年級學生在3次分數教學活動中產生的日志文件，德國慕尼黑理工大學的Frank Reinhold等學者對以上數據進行了聚類分析，發現了學生體現出4種不同的參與程度．而帕德博恩大學的Sebastian Rezat利用MAXQDA，對多個三年級學生在實驗環境和真實環境中使用數字教材的錄像進行編碼及聚類分析，將學生在教學中的應答模式分成3種類型，并根據學生的使用情況對數字教材的開發提出了建議．

6.2 數字平臺的應用

通過視頻教程和在線適應性數學活動和游戲來支持數學學習者，以及教師準備課程、選擇任務、評估學生的理解和技能，并與同事協作的數字平臺在K-12年級和高等教育中十分普遍．會議中對一些數字平臺的特點進行了介紹．

美國的動態評估項目（ongoing assessment project）始于2003年．基于對學生學習的研究，OGAP為教師提供了一整套形成性評估工具、資源和使用說明，以幫助他們系統地、持續地在學生的學習路徑上回應他們對核心概念的理解．OGAP的評估過程基于評估—分析—回應循環，其框架綜合了問題情境、知識結構和學習路徑，教師可以利用以上支持來分析學生的作業并確定教學的進一步規劃．最近的研究表明，OGAP的使用在學生解決問題的準確性和策略使用上，以及教師對學生思維的理解上有顯著的促進作用．

STEP（seeing the whole picture）是一個在線數學形成性評價平臺．STEP可以對學生答案進行自動批閱，尤其對于那些基于不同的數學推論，需要學生構建不同示例，具有很強開放性的任務，這里被稱之為EET任務（example eliciting tasks）．STEP中EET被設計成有許多可能的正確答案，這些答案可以根據不同的特征進行自動分析．其作答分析不但可以為基于學生學習錯誤的研究或實踐提供幫助外，還可以根據學生作答中出現的數學對象的不同特征，分析學生作答的生成過程．在課堂上，STEP可以為教師提供對于學生水平的實時學習分析．

而還有一些研究者重點關注數字平臺對教師、學生的影響．美國肯特州立大學的Scott A. Courtney介紹了俄亥俄州的數字平臺是如何幫助當地農村地區六~十二年級的數學教師、教學干預專家和大學數學教育研究者在網上協同工作，給予農村學生在數學上的巨大支持，以幫助他們進入大學或者進行職業教育．

在課程改革背景下，法國于2017年開放了兩個數字平臺（CARTOUN與DRSB）．其中，CARTOUN允許教師相互分享教學設計，而DRSB則儲存了教師教學所需的大量資源．法國布雷斯特大學的Ghislaine Gueudet對以上兩個平臺進行了分析和比較．他首先觀察教師是如何利用以上兩個平臺進行教學設計，再去分析兩個平臺與其它資源、軟件的兼容程度．研究表明，可以通過以上兩種方式來調查數字平臺在教師中的使用狀況．

荷蘭埃因霍溫理工大學的Birgit Pepin與Zeger-Jan Kock從宏觀和微觀兩個層面，對荷蘭政府資助的數字教育平臺（WIKIWIJS）進行了分析．結果表明，在宏觀層面，研究者發現平臺支持開放共享資源的創建、修改和使用，這些資源可以鏈接到平臺內外的資源；平臺還支持教師共同制作資源；通過將教育相關的元數據附加到數字資源上，增強了平臺的搜索功能，從而使教師更容易訪問各種存儲庫和數據庫中的資源．在微觀層面，該平臺可以在一個主題與相關知識、不同概念或不同主題的領域和學科之間建立聯系．但WIKIWIJS不提供教師之間，或師生之間的交流平臺，也不提供關于學生學習的數據存儲（例如，測試結果）．研究者認為，該平臺有可能改變教師的文檔工作習慣．

丹麥奧爾堡大學的Andreas Lindenskov Tamborg和Morten Misfeldt調查了“數字平臺”對教師教學的局限與支持．研究者用兩個例子說明數學教師在使用這些平臺時所受到的啟示和約束．結果表明，使用平臺的效果取決于教師是否遵循平臺的理念和方法．但研究者認為，在平臺與教育系統的關系上，各國之間存在著巨大的差異，平臺是由國家集中開發的，還是由私人公司開發的？開發這些平臺的目的是什么？它們是教師自愿使用的嗎？這些問題的答案對數學教師的工作都有著重要的意義．

需要注意，雖然信息技術在幫助學生學習的過程中起到了關鍵的作用，但也暴露出一定的問題．智利學者Alex Montecino與Melissa Andrade-Molina發現，隨著信息技術逐漸滲入智利的課堂，智利教育上的兩極分化現象進一步加重．其原因在于，信息技術所發揮的威力取決于他們的使用者，即教師和學生所具有的能力．

7 對中國數學教材研究的啟示

由以上分析可知，此次大會對中國數學教育研究有如下4點啟示．

7.1 應重視數學教材研究中的理論構建

無論是教材開發、教材內容的呈現、教材的比較、教材的使用等方面，理論框架占據重要的地位．例如，多位學者將ATD理論、四面體理論、符號學理論、項目學習理論應用于教材的分析和開發．另外，在教材與教師、學生之間的關系上，也有專題組進行相關研究．這說明在教學中，教材不是獨立存在的，而與其它要素之間存在密切的關系，這在教材開發、使用和評價中都需要重點關注．

7.2 應重視信息技術和數字教材的研究與開發

在此次會議的所有主題中，均包含數字教材的開發、研究和評價，基于互聯網的智慧學習平臺與數字教材也已經成為熱點話題．隨著信息技術的發展，科技在數學教育中發揮的作用與日俱增，其不但可以顛覆課堂教學的傳統模式，更為中國學者了解學生的數學學習過程提供數據支持，因此數字教材的開發、實驗、推廣和使用研究應該成為中國未來數學教材研究的重點．盡管信息技術在改變學生學習方式，提高教育公平性上具有重要的作用，但也會加大教育資源兩極分化的趨勢．以色列海法大學的Shai Olsher指出，教師的水平會極大地影響教師對資源的選擇和使用．因此，如何加強教師培訓使得教師可以合理地使用教學資源，減少兩極分化也是中國數學教育工作者亟需關注的問題．

7.3 應重視不同階段教材的比較研究

國外學者在教材內容的編排順序及呈現方式上進行了細致的研究，但這些研究主要集中在小學階段，中學、大學階段的教材研究較少，因此建議中國研究者應重視中學數學教材，乃至大學數學教材的研究．在教材編寫過程中，編寫者應注意不同學段教材間的表述差異，以幫助學生更好地完成學段銜接；在編寫過程中，應從多個角度對概念進行定義，并設置相應的任務以幫助學生完成多元表征間的轉換．在教材比較上，參會學者不僅關注了教材間的橫向比較研究，也關注了教材的縱向比較研究．教材比較研究有助于研究者借鑒不同版本的數學教材的優點，各國教材比較的異同反映了教材在社會文化和功能定位上的差異．對這些差異進行合理、有效的解釋，有助于中國更好地開發有利于數學學習的教材．

7.4 應重視教材的動態性與廣義性及應用性

南非威特沃特斯蘭德大學的Jill Adler在她的主題報告中指出，近20年來數學教育中的“教材（或資源）”在3個維度上發生了重構．一是“資源”由一個名詞轉變為一個動詞，即意味著研究的重心轉變為教師在實踐中是如何與資源進行互動的；二是“資源”的概念發生了拓展，除了傳統的實體教學用具外，網絡資源，甚至學生所處的社會文化環境，都可以視為廣義的“資源”；三是關于“資源”的理論導向也發生了變化，在學校教學中，更加重視將“資源”與學生的日常生活及動手實踐相聯系，這些都為研究者更好地看待教材和資源提供新的視角．同時也應該認識教師在教材使用中的關鍵作用．南非威特沃特斯蘭大學的Moneoang Leshota指出，當教師不能完全理解教材編寫意圖時，教師難以發揮教材在教學中的應用價值．因此建議教材編寫人員應加強與一線教師及教研員的交流．

[1] BIKNER-AHSBAHS A, PREDIGER S. Networking of theories as a research practice in mathematics education [M]. New York: Springer, 2014: 76–91.

[2] VILLIERS M D. The role and function of a hierarchical classification of quadrilaterals [J]. For the Learning of Mathematics, 1994, 14 (1): 11–18.

[3] CHANG B L, CROMLEY J G, TRAN N. Coordinating multiple representations in a reform calculus textbook [J]. International Journal of Science and Mathematics Education, 2015, 14 (8): 1?475–1?497.

[4] REZAT S. From the didactical triangle to the socio-didactical tetrahedron: Artifacts as fundamental constituents of the didactical situation [J]. ZDM, 2012, 44 (5): 641–651.

The Review of the Third International Conference on Mathematics Textbooks Research and Development

QI Chun-xia, CAO Chen, FU Yu

(Beijing Normal University, Beijing 100875, China)

The Third International Conference on Mathematics Textbook Research and Development in 2019 mainly included the theory of textbook research, textbook development, textbook content, textbook history, textbook comparison,textbook research, digital textbook and other topics. After analyzing the conference papers and conference speeches, we could summarize the latest views, achievements and directions of international mathematics textbook research, and provide some reference for the research of mathematics textbook in China.

textbook content presentation; textbook comparison; textbook history; digital textbook

G423.3

A

1004–9894（2020）02–0089–05

2019–12–18

北京師范大學未來教育高精尖創新中心項目——中學數學學科診斷分析工具開發與應用研究（BJAICFE2016SR-008）

綦春霞（1966—），女，山東東營人，教授，博士生導師，主要從事課程比較、數學教育研究．

綦春霞，曹辰，付鈺．第三屆國際數學教材研究與發展會議綜述[J]．數學教育學報，2020，29（2）：89-93．

[責任編校：周學智、陳雋]