例談探究式解題課教學

朱清波，曹廣福

例談探究式解題課教學

朱清波1，曹廣福2

（1．廣州市執信中學，廣東 廣州 510090；2．華南農業大學，廣東 廣州 510005）

闡述了解題課的基本功能，指出了目前中學數學教育中解題課存在的問題．通過對一道平面幾何題的分析，討論了解題課環節如何創設一系列探究式問題，引導學生從問題的條件出發通過特例、試錯等方法猜測一般規律并找到解決問題的方法，反思是如何想到這樣的方法的？進一步對解題方法的優劣進行評判．通過方法的探究過程培養學生的元認知以及提升學生對數學方法的價值與審美判斷能力．

探究式；解題課；元認知；數學素養

1 問題提出

中學課堂通常分“概念課”“原理課”“解題課”3種課型，“復習課”可以歸類到“解題課”．解題課是中學數學教學中非常重要的課型，也是教師們十分重視的教學環節．很多教師甚至把解題課比概念課、原理課看得更重，付出的精力更多．然而目前解題課普遍存在的問題是：課堂上反復刷題，提高學生解題的熟練度，缺少提升學生思維能力的考量．從高考的考題情況分析，除了最后的壓軸題，大多數題更多地依賴于考生的解題熟練度．刷題越多，遇到類似題型的幾率就越大，得分率也就越高．考試是根指揮棒，有什么樣的考試，就會有什么樣的教育方式，因此，改善基礎教育現狀的著眼點或許是考試方式．然而，涉及千萬學子的考試改革不是一件一蹴而就的事情，需要逐步進行．考試是檢驗教育效果的一種方式，并非目的，從教育的角度看，教學不能淪為考試的奴隸，考試與教學的關系不應該本末倒置．但考試作為一種重要的選拔方式，在很大程度上決定了考生們的未來，教學不顧及考試的效果是不現實的．這就存在一個數學素養的提升與應試之間如何平衡的問題．解題課在這個平衡中無疑充當了至關重要的角色，把握得好，可以二者兼顧；把握不好，可能二者皆失．研究者從一則普通的幾何題出發，層層拓展，分析在解題課教學中如何引導學生拋開慣性思維，不是基于經驗，而是從問題自身的條件出發尋找解決問題的思路，并從中發現有規律性的現象，從而達到舉一反三的效果．

2 解題課在數學教育中的作用

哈爾莫斯說：“學習數學的唯一方法是做數學．”[1]適度地解題是數學學習必不可少的環節，但教師應該選擇具有啟發性的好題，通過這類問題能夠讓學生發現其中所蘊含的規律，起到觸類旁通的效果．

解題課的功能是什么？這是需要首先搞清楚的問題．解題課的功能是在概念課、原理課基礎上固化已學的概念、原理、思想與方法，并能熟練運用它們解決問題．其基本特征即探究式或研究式解題，關于探究式教學模式有一個相對傳統的解釋：“探究性教學模式不僅可以較深入地達到對知識技能的理解與掌握，更有利于創新思維與創新能力的形成與發展，即有利于創新人才的培養．在此過程中，能否取得成就的關鍵是，學生在學習過程中的主體地位是否能得到比較充分的體現，同時還需要有教師方面的引導、幫助與支持．換句話說，探究性教學模式的成功實施涉及兩個方面——既要充分體現學生在學習過程中的主體地位，又要重視發揮教師在教學過程中的主導作用．離開其中的任何一方，探究性學習都不可能有良好效果．可見，‘主導—主體相結合’是這種教學模式的基本特征．”上述定義稍顯籠統，并未解釋清楚什么叫“探究”．

探究式解題是指教師針對給定的問題從條件出發，創設一系列引導式問題，形成一個層層遞進的問題鏈，引導學生尋找解決問題的思路，其理論基礎是弗賴登塔爾的“數學教育是數學的再創造”．眾所周知，數學并非是一門演繹科學，當人們試圖解決一個數學問題時，并非僅僅是羅列一些條件，然后進行推理．實際上，解決問題是一個不斷摸索、試錯、猜想、檢驗的過程．解題課不僅為了固化已學的概念、原理，同時也是培養學生解決數學問題正確方法的重要環節．與數學家研究過程不同的是，學生的認知能力與知識積累有限，不可能像數學家那樣完全獨立地研究數學問題．事實上，數學教育是在教師引導下學生的“有限再創造”過程．換言之，教師需要通過一系列引導式問題啟發學生尋找解決問題的思路．然而，實際的解題課常常是通過重復訓練達到一定的解題熟練度，從而提高應試效率．實踐表明，重復訓練可以有效增加學生的解題經驗與熟練度，憑借經驗解決相對比較熟悉的題型，從而提高解題速度，它對于應付選拔式考試具有一定的效果．

無論出于提升分析問題解決問題的目的還是應試的目的，兩者并無根本矛盾，考試的初衷也是為了檢驗考生掌握概念、原理、思想與方法的程度，檢驗學生的數學素養與運用數學理論與方法解決問題的能力．所以，一方面，作為指揮棒的選拔式考試需要改革，使之能真正促進素質教育與考生數學能力的提升；另一方面，課堂教學要兼顧素養與應試兩個方面．概念課與原理課兩個教學環節不能弱化，關于該問題，已經有一些論著論及（見文[2-7]）．但關于解題課如何兼顧素養與解題能力的提升，相關的研究并不多見．很多關于解題課的討論都是基于如何解題的，糾纏于解題技巧與細節者較多，缺少解題課對學生思維能力提升方面的剖析．研究者認為，探究式解題課至少應該在教師引導下完成3個方面的教學環節：（1）如何從問題的條件出發通過特例、試錯等方法猜測一般規律？（2）如何在前述基礎上找到解決問題的方法并反思是如何想到這個方法的？（3）什么是好的方法？第一個環節屬于方法的探究過程，第二個環節本質上屬于元認知問題，第三個環節則涉及對數學方法的價值與審美判斷．

當然，在探究式解題基礎上進行適度的解題訓練也是需要的，尤其是引導學生通過解題訓練進而學會題型與方法分類，對于增加解題經驗、提高解題速度無疑是有幫助的，但這已超出本論題的范圍．

3 一道平面幾何題的思考

平面幾何是初中數學的重要組成部分，傳統的平面幾何邏輯性與系統性都比較強．新課標下的平面幾何在此方面有所弱化，更注重與代數之間的聯系，生活化的味道也相對濃了一些．幾何是培養學生的直觀思維與邏輯推理能力的重要載體，如何通過幾何問題提升學生的思辨能力值得探討．

下面這道題的難度中等偏下，有解題經驗的學生并不難找到它的解答：“正方形內一點與4個中點依次連接，得到4個區域，其部分區域面積如圖1所示，求剩余區域面積．”

這道題蘊含著一個非常有趣的一般規律，如何發現這樣的規律則是件有難度的事情．

該題如果出現在解題課上，學生由于清楚了多邊形的面積以及計算多邊形面積的一般方法，那就是化多邊形為三角形或特殊的多邊形（例如矩形、平行四邊形、梯形等），所以，學生很容易想到的一種方法就是把上述圖形分解成若干三角形：

點在正方形內部時，相對的兩個區域面積之和相等，即Ⅰ+Ⅲ=Ⅱ+Ⅳ，連接4個頂點，如圖2，每塊區域利用中點平均分成2塊，共8塊，重新組合成4塊大區域，即：

對比可知：?+20=32+16，

故 ?=32+16-20=28 cm2．

由于已經有了前期的經驗積累，因此，學生想到上述方法并不奇怪．

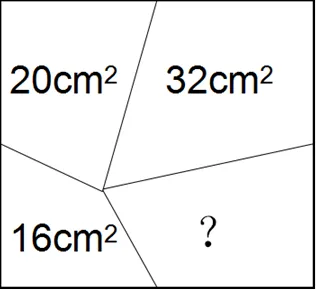
圖1 正方形區域面積

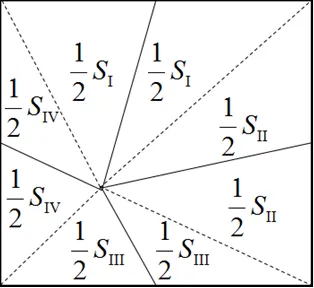
圖2 正方形分割

還有一種分割方法也不難想到，那就是連接正方形4條邊的中點（如圖3），也可完成對4個多邊形的三角剖分．

從圖形結構來看，4塊區域都有一部分面積相等的小區域，同時去掉后，還是一個小正方形，在新的正方形中探究這些小區域的面積關系（如圖3）．記4個新區域面積分別為Ⅰ、Ⅱ、Ⅲ、Ⅳ，則有：

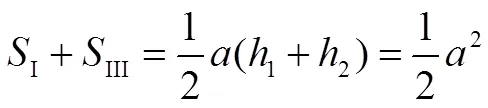
所以Ⅰ+Ⅲ=Ⅱ+Ⅳ，同時增加4個全等等腰直角三角形后，上述規律保持不變，故?=32+16-20=28 cm2．

看起來上述問題似乎已經得到解決，但有一種情況可能會出現，大正方形內的點有可能不在小正方形內部（如圖4）：設內點為，當在小正方形外（同時在大正方形內）時，區域的劃分會顯得復雜．為方便起見，記Ⅰ=△PEF，Ⅱ=△PFG，Ⅲ=△PGH，Ⅳ=△PEH,同理可推得Ⅰ+Ⅲ=Ⅱ-Ⅳ．這說明若點不在小正方形內部,需將兩個面積相減．

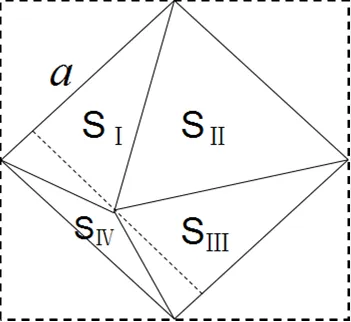
圖3 多邊形的三角剖分

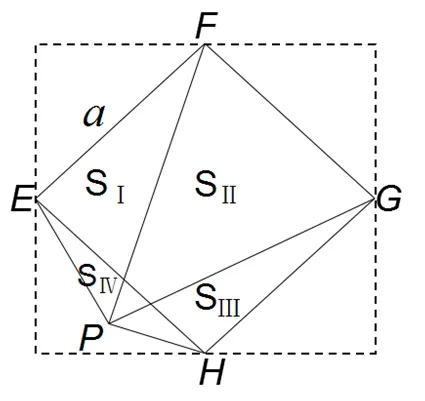
圖4 正方形內的動點

上述兩個方法的思路是類似的，出發點都是試圖將四邊形分割成三角形，利用“三角形等底等高則面積相等”這一性質完成問題的解答．但顯然第一個方法比第二個方法更簡潔，避開了可能出現的分類討論．所以從方法上評判，第一個方法比第二個方法更優．

然而，以上方法都是基于經驗，經過了訓練的學生都不難發現這類解題思路，但它們是不是好的方法？什么叫好的方法？通常有幾個判斷標準：簡潔，抓住了問題的本質，方法具有一般性．

上述問題的本質是什么？如果把問題稍微變換一下，類似的結論是否還成立？類似的方法是否還適用？例如，若是把正方形換成矩形呢？或者把正方形邊界的中點換成更一般的點呢？此時的問題沒有發生本質的變化，上述兩個方法依然是適用的．如果將正方形換成圓（到了高中甚至可以換成橢圓）呢？類似的結論是否還成立？這就涉及問題的本質與方法的一般性討論了．一旦邊界是“彎曲的”，第一種方法顯然就不能照搬了，因為用此方法無法將4個小區域分割成三角形．第二種方法或許可行，將圓周上的4個等分點連接之后，得到了4個面積相等的曲邊區域，割掉這4個小區域后得到一個正方形，問題回到了正方形的情形．從這個角度看，第二個方法比第一個方法更具有一般性．換言之，第一個方法更具簡潔性，第二個方法更具一般性．所以兩種方法各有千秋，優劣在伯仲之間．

還有其它方法嗎？這就需要暫時擺脫化多邊形為三角形的慣性思維，以對問題本質的探索作為出發點尋找新的方法．

數學研究的一個基本特征是從特殊到一般．姑且不管是何種區域，問題的關鍵是區域內一點與區域的4個邊界點連接得到4個不同的子區域，這4個子區域之間的關系與內部點的位置是否有關？不妨先從特殊的點出發考察一下這些子區域之間的關系．例如，若內部的點是正方形的中心或者在正方形的一條中線上，結果如何？此時將會發現一個共同的規律：相對的兩個區域面積之和相等．再考察更一般情形，中線上的點發生了偏移，變成了正方形內的任意一點，類似的現象是不是還會出現？這樣的思考方式有效避開了分割多邊形為三角形的慣性思維，雖然最終還是需要利用三角形的面積，但這是探索出來的必然方法，而不是經驗的結果，這也是進行科學研究的普適性思維，兩者不可同日而語．

不妨先探究一下第三種解答：連接對邊中點、，相交于點（如圖5），連接、、、、，因為是對稱中心，有△POE=△POG，△POF=△POH，同時減去公共部分后有①+②=③+④（數字符號代表區域面積）這說明相對的區域面積總是“相互補充的”（即某塊區域面積增加，其對角區域面積會減少相應部分），且對角區域的面積之和為全部面積的一半，對比原圖，則必然有?=32+16-20=28 cm2．

上述解法的出發點并非化多邊形為三角形，雖然最終還是用到了三角形面積之間的關系，但這種關系建立在探索的基礎上而不是經驗的基礎上．更重要的是，第三種解答抓住的是區域內部點的位置，沒有直接去關心邊界，這也就使得這種方法具有了普適性．邊界是不是直的并不重要，最終需要的并非正方形圖形本身，而是正方形的對稱性．只要保證交點是整個平面圖形的對稱中心，即可讓“對角區域面積之和為定值”這一性質得以保留，因為中心對稱圖形的對稱中心可以保證原始劃分中的對角區域面積之和相等，這可以從平行四邊形和橢圓這兩種特殊圖形中加以檢驗．

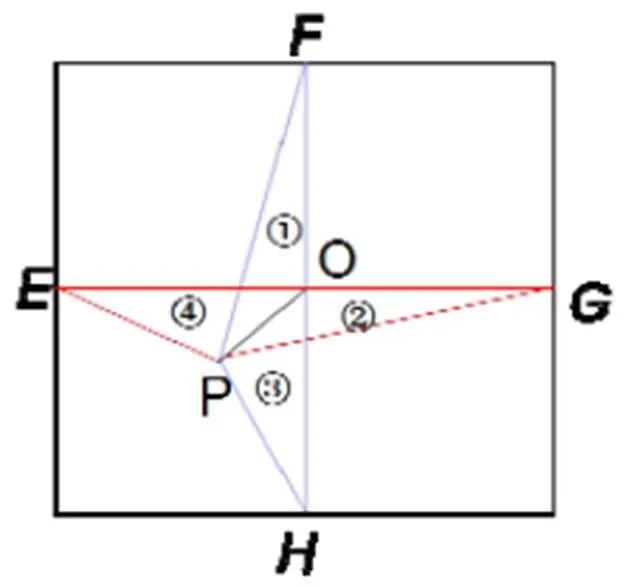
圖5 正方形對邊中點連線

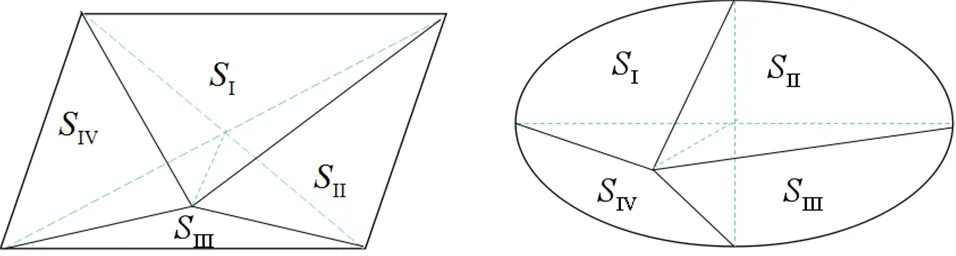
兩種圖形均滿足SⅠ+SⅢ=SⅡ+SⅣ．

4 解題課課例設計

以上述問題為例，如何在解題課中引發學生去思考從而尋找解決問題的最佳方法，進而提升思維能力？

通過如下一系列問題的設計層層遞進，可以引導學生深入思考．

問題1：正方形內一點與4邊中點依次連接，得到4個區域，其部分區域面積如圖1所示，求剩余區域的面積．

相信無需多少時間，就會有學生給出解答，學生給出的解答很可能是前面的第一種解法．如果學生無法回答，不妨輔以這樣的問題：一般的多邊形面積如何計算？有了這樣的提示后，學生是可以想到化多邊形為三角形的．如果學生給出了上述兩種不同的解答，則直接進入問題3，否則先考慮下面的問題2．

問題2：這是分割多邊形為三角形的唯一方法嗎？

學生如果了解了第一種方法，很容易想到另一種分割方法，所以這個問題的回答對于學生應該沒有多少難度．

問題3：上述幾種方法哪種方法更好？好在哪里？

這個問題的提法可能令學生一頭霧水，不知從何回答，不妨問得更具體一點：哪個方法更簡潔？哪個方法更具有一般性？

問題4：上述方法的缺陷是什么？除了將多邊形分割成三角形，還能想出別的辦法嗎？

在分析這個問題的過程中應該同時闡明問題的重要性，上述兩種方法僅適用于多邊形，一旦區域的形狀發生變化，這種方法可能就不適用了，但類似的結論是否仍然成立？例如將正方形換成圓怎么辦？此時學生或許會想到第二個辦法也適用于圓，但如果換成更一般的對稱區域呢？通過對這個問題的分析，可以幫助學生了解：分割多邊形的方法依賴于區域的形狀．它僅適用于正方形或平行四邊形，如果邊界彎曲，就要想辦法把邊界割成多邊形，所以第二種方法才更具有一般性，但它仍然具有局限性，因為如果是更一般的區域，第二種方法可能也不適用．這兩種方法之所以具有局限性，根本原因就在于兩種方法都需要轉換成多邊形才能利用三角形面積完成計算．在此基礎上拋出下面更一般的問題．

問題5：假設兩條直線交于區域內一點，與區域邊界分別交于點、、、（如圖7），構成一個平行四邊形．線段與將區域分割成4塊小區域，使得相對的兩塊區域面積之和等于整個區域面積的一半．任取區域內一點，與、、、的連線將區域分成4個小的區域，相對的兩塊區域面積之和是否仍是整個區域面積的一半？為什么？

這個問題中的區域很寬泛，甚至不必要求它是中心對稱圖形，只要過區域內部一點的任意兩條線段被點平分且能將區域分割成4塊小區域使得相對兩塊區域面積之和等于整個區域的一半，那么這4個點就決定了區域內任意點的性質：到4個邊界點連線得到的4個小區域相對區域面積之和相等．有了前面的分析基礎，學生已經不難應對這個問題．這個結論與區域形狀無關，只與分割區域的兩條直線的位置有關．在此基礎上還可以進一步拓展：

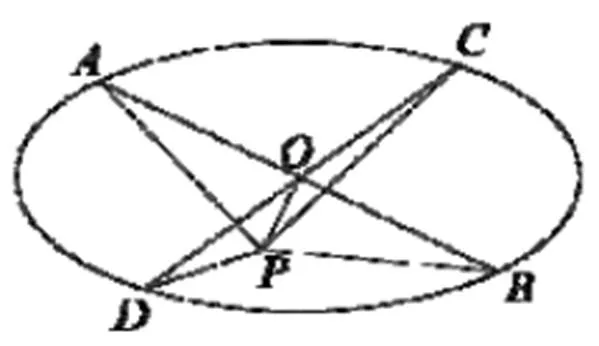
圖7 兩條直線分割區域

問題6：是不是所有的區域都能找到兩條相交直線具有問題5中所說的性質？

這個問題的難度比較大一些，可以作為課外思考題，供有余力且有興趣的學生思考．其基本的思路是：（1）有沒有一條直線將一個給定的區域面積平分？這個問題不難有肯定的回答；（2）過平分區域面積的線段之中點是否存在一條直線將區域分割成具有問題5中所說性質的4塊小區域而且交點也是該線段的中點？結論就未必了．不妨把問題5中所說的性質稱為區域面積對分性質．

定義1 假設區域的邊界上有4個點，內的點到這4個邊界點的連線將區域分割成4個相對的區域面積之和相等的小區域，則稱為相對于這4個邊界點的區域面積對分點．如果區域的邊界上存在4個點，使得區域內的任意點相對于這4個邊界點都具有面積對分性質，就稱該區域具有面積對分性質．

由此可以得到一個一般性的結論，不妨讓學生總結成一個定理：

定理1 假設是中心對稱的有界凸區域，則具有面積對分性質．

以上一系列問題的分析體現了探索的一般思維方法，思維能力正是在這種探索中慢慢形成的．當然，由于時間所限，所有的解題課都如法炮制顯然是不現實的，正如前文所說，需要考慮到素養、能力與應試之間的平衡．定期進行一些類似的探究式解題，學生慢慢就能掌握分析問題過程中的探究方法．

可以作為課外的研究習作，引導有興趣并有余力的學生圍繞著這個問題進一步展開討論．

問題7：定理1中的中心對稱條件是不是必需的？區域的凸性是不是必需的？

中學雖然沒有專門介紹凸區域的概念，但此概念并不抽象，學生在理解上并無難度．通過具體的例子很容易發現，如果區域不是凸的，就不能保證區域內任意點到邊界點的連線都在區域中，面積對分性質可能不成立，所以區域的凸性是必要條件．那么，中心對稱性條件是否可以去掉呢？此時，不妨引導學生先考慮特殊情形，例如，三角形情形如何？凸四邊形情形又如何？通過分析會發現，三角形與凸四邊形區域都可以通過連接各邊的中點得到一個平行四邊形（其中三角形為3邊的中點加上任意一個頂點）．但到了五邊形以上的情形，類似方法就不適用了．問題的焦點集中在能否找到具有類似對稱圖形中心性質的那種點？利用凸區域邊界的連續性可以證明，所有的凸區域都存在一個內接平行四邊形，該平行四邊形對角線交點就是這樣的點．換句話說，該平行四邊形的對角線將凸區域分成了4塊相對區域面積之和相等的小區域，因而凸區域內的任意點相對于該平行四邊形的4個頂點都具有面積對分性質．于是得到一個更一般的結論：

定理2 假設是平面內的有界凸區域，則具有面積對分性質．

5 結束語

概念課、原理課與解題課是數學教學過程中3個不可或缺的基本課型，無論是為了強化對概念、原理的理解與靈活運用，夯實數學基礎，提升數學思維能力與數學應用能力還是為了應試，解題課都起著舉重輕重的作用．探究式解題對于強化學生對數學概念、原理的理解，提升數學思維能力與解決問題的能力無疑是有幫助的．在現實的大背景下，兼顧學生數學素養的培育與解題的熟練度是解題課需要肩負起的重任．

[1] 哈爾莫斯．怎樣做數學研究[EB/OL]．（2019-04-16）[2019-06-12]．https://chuansongme.com/n/2909741451012．

[2] 曹廣福．課標與教材淺議[J]．課程·教材·教法，2016，36（4），12-16．

[3] 何勇，曹廣福．課堂教學中如何兼顧學生素養與應試能力[J]．數學教育學報，2014，23（2）：63-65．

[4] 張蜀青，曹廣福．以問題驅動對數概念課教學[J]．中學數學教學參考，2014（7）：12-13．

[5] 張蜀青，曹廣福．以問題驅動的原理課教學[J]．中學數學月刊，2014（8）：34-35．

[6] 張蜀青，曹廣福．大學教師與中學教師關于《基本不等式》的“同課異構”評析[J]．數學教育學報，2015，24（6）：40-43．

[7] 曹廣福，張蜀青．問題驅動的中學數學課堂教學（理論與實踐卷）[M]．北京：清華大學出版社，2018：1．

Inquiry Teaching of Solving Problems by Examples

ZHU Qing-bo1, CAO Guang-fu2

(1. Guangzhou Zhixin High School, Guangdong Guangzhou 510090, China; 2. South China Agricultural University, Guangdong Guangzhou 510642, China)

Problem-solving lesson is an important link to help students solidify knowledge and learn to use mathematical knowledge to solve problems in classroom teaching. Traditional problem-solving lesson pays attention to cultivating students’ proficiency in solving problems and lacks consideration of improving students' thinking ability. The function of problem-solving lesson has two levels, one is educational level, the other is utilitarian level. Through the analysis of a plane geometry problem, this paper discusses how to guide the students to think that what methods can we think of in the face of a problem, and how do we think of this method? What is the best way? Through the inquiry process of methods, students’ meta-cognition is trained and their value and aesthetic judgment ability of mathematical methods are improved.

inquiry; problem solving course; meta-cognitive; mathematical literacy

G622.4

A

1004–9894（2020）02–0049–04

2019–11–06

國家“萬人計劃”人才項目——問題驅動的中學數學課堂教學

朱清波（1978—），男，中學高級教師，主要從事數學教學與數學教育研究．

朱清波，曹廣福．例談探究式解題課教學[J]．數學教育學報，2020，29（2）：49?52．

[責任編校：陳漢君、陳雋]