基于AHP理論的數學高考試題綜合難度模型構建與應用

武小鵬，孔企平

基于AHP理論的數學高考試題綜合難度模型構建與應用

武小鵬1，2，孔企平2

（1．黔南民族師范學院 數學與統計學院，貴州 都勻 558000；2．華東師范大學 教師教育學院，上海 200062）

高考作為中國高利害性考試，其試題的難易程度直接影響著測試的質量和測量的公平性，綜合難度系數模型能夠在測試前對試題的整體難度做出評估，為有效合理的測量提供了保障．綜合難度系數模型認為，影響數學高考試題難度的因素分為背景、是否含有參數、運算水平、推理能力、知識含量、思維方向、認知水平7個因素，各因素之間分為不同水平．研究選取16位數學學科專家對綜合難度系數各因素與不同水平的難度做出比較評判，在此數據的基礎上采用層次分析理論（AHP）對不同因素的權重和同一維度中不同水平的權重進行求解，進而建立了更為切合實際的綜合難度系數模型．利用該模型對2019年理科數學全國Ⅰ和全國Ⅱ卷進行評價，并對該模型的應用前景和未來研究的方向進行了討論．

層次分析法；測試項目；綜合難度；數學高考；難度模型

教育測評作為一項非常重要且又十分復雜的教育活動，它對整個教育起到“牛鼻子”的引領功能[1]．測試作為學習者學習結果檢測和教育教學效果監測的重要方法，在整個教育過程中得到廣泛的使用．一項測試項目的質量往往受到多個因素的影響，如測試的信度、效度、區分度和難度等．然而在這些因素中試題的難度最能引起社會的高度關注．試題的難度在一定程度上影響著測試的公平性，尤其是在高利害性的測試中，難度更能夠決定應試者的成敗，如中考、高考、研究生入學考試等．然而，目前對難度的計算都是在測試完成后，基于測試數據得到的，雖然這種計算難度的方法比較科學[2]．但是大多高利害性的測試都不允許提前大規模預測，以免造成試題曝光，導致試題泄漏．現有的評價注重綜合性，在評價的意義上分析，已超越了僅僅依靠定量評價的自然方法論[3]．綜合難度系數模型從影響測試項目的因素出發，依據數學學科特點對測試項目進行深入的邏輯分析，能對測試項目的難易程度提前做出預判，能夠較大幅度提升測試的質量[4]．雖然綜合難度系數模型已有較多的研究者在不同學科領域做了研究，如數學[5–6]、物理[7]、地理等[8]，但是對于難度系數模型中各因素之間的權重和同一因素中不同水平之間的權重計算存在很大的弊端．各因素之間一般采取簡單相加，不同水平之間也采用簡單的1、2、3分的主觀記分方式．這里采用專家評分的方式，借用AHP理論對該模型中的權重進行計算，進一步完善了綜合難度系數模型，使得模型更加貼近實際情況．

1 綜合難度系數模型

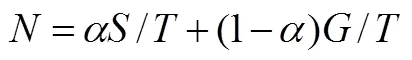
綜合難度系數模型是對表1中的因素和水平進行有效的加權，聚合成一個指標的過程．因素的難度系數為d：

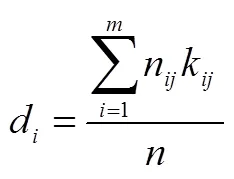
表1 測試項目的綜合難度系數模型界定

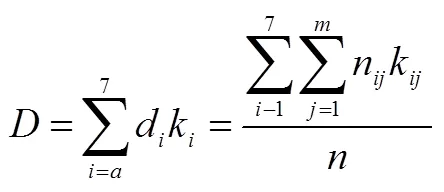
其中，k是指第個因素的權重系數．

該模型充分考慮到不同影響因素對整個測試項目難度的影響．但在模型求解過程中，不同因素的權重系數k和同一因素中不同水平的權重系數k是未知的．已有研究的做法是方便權重，即認為k都等于1，k則按照從低到高的水平分別為1、2、3等．這種計算方法顯然存在較大的問題．權重的大小沒有科學依據．以下研究以專家評判的方式，利用AHP理論計算得出k與k的值．從而較為科學地完善了綜合難度系數模型．

2 基于AHP的權重計算方法

1990年，Satty教授“如何做決定——層次分析的過程”一文中提出了計算不同影響因素權重的方法[16]．該方法歸結起來由以下4個過程構成[17]．

2.1 構造判斷矩陣

在計算不同影響因素的權重系數之前需要給不同的指標進行重要性排序，排序通常用9點法評分，標度表如表2．

表2 指標評分標度

依據以上評分規則，可建立判斷矩陣，

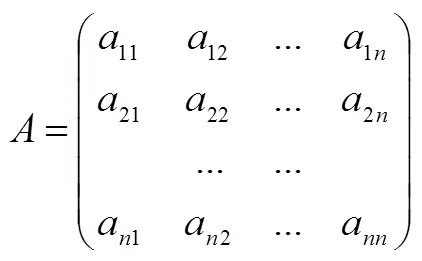
其中a表示第個指標與第個指標相比得到的標度．

2.2 權重系數的計算[18]

2.3 權重系數的一致性檢驗

通常一致性檢驗指標采用[19]

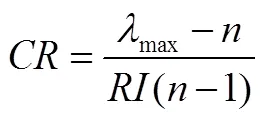
表3 RI取值

當≤0.01，權重系數具有可接受的一致性．

3 綜合難度系數模型中各權重系數的建構

為了較為合理地獲得權重系數，利用專家法構建評判矩陣．專家組由16人組成，其中6人是具有多年教學經驗的教學名師，有深入的一線教學經驗和應試能力，10人為具有試題研究經歷的博士研究生，部分博士具有奧賽研究和輔導經歷．通過專家組評判得到評分標度數據．

3.1 各因素的權重系數計算

依據上述計算方法，通過對16位教師計算的結果求平均找近似的方法得到了如表4的數據．

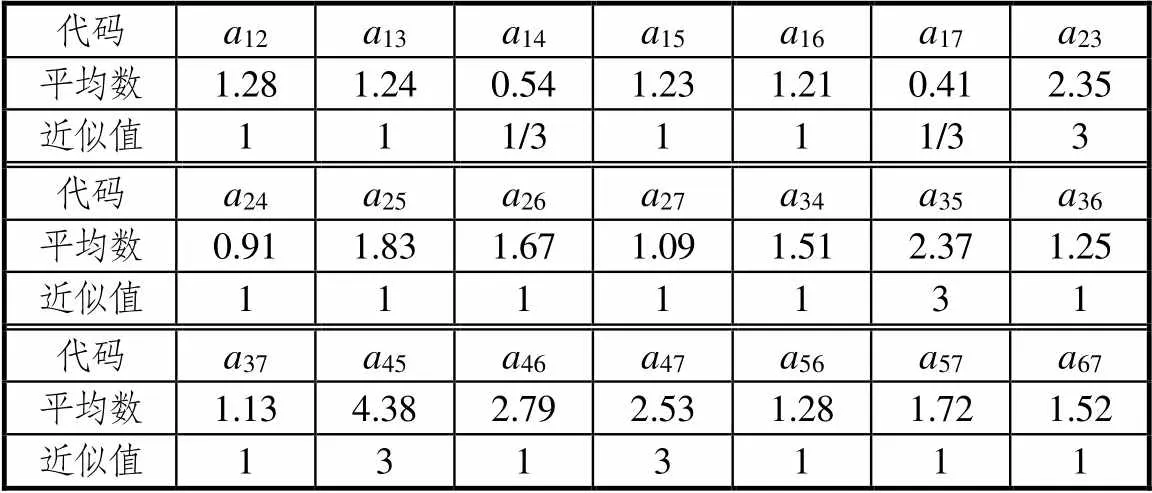
表4 各因素標度值

因此，不同因素的判別矩陣為：

在層次分析法中，判別矩陣的計算方法可以將人主觀評判進行定量化的分析，這是將定性描述轉化為定量計算的重要環節[20]．依據進一步計算得到

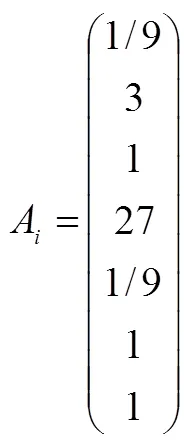
3.2 不同水平的權重系數計算

依據專家對不同水平的評判結果和AHP理論對權重的計算方法，得到不同水平權重系數計算信息表，如表5所示．

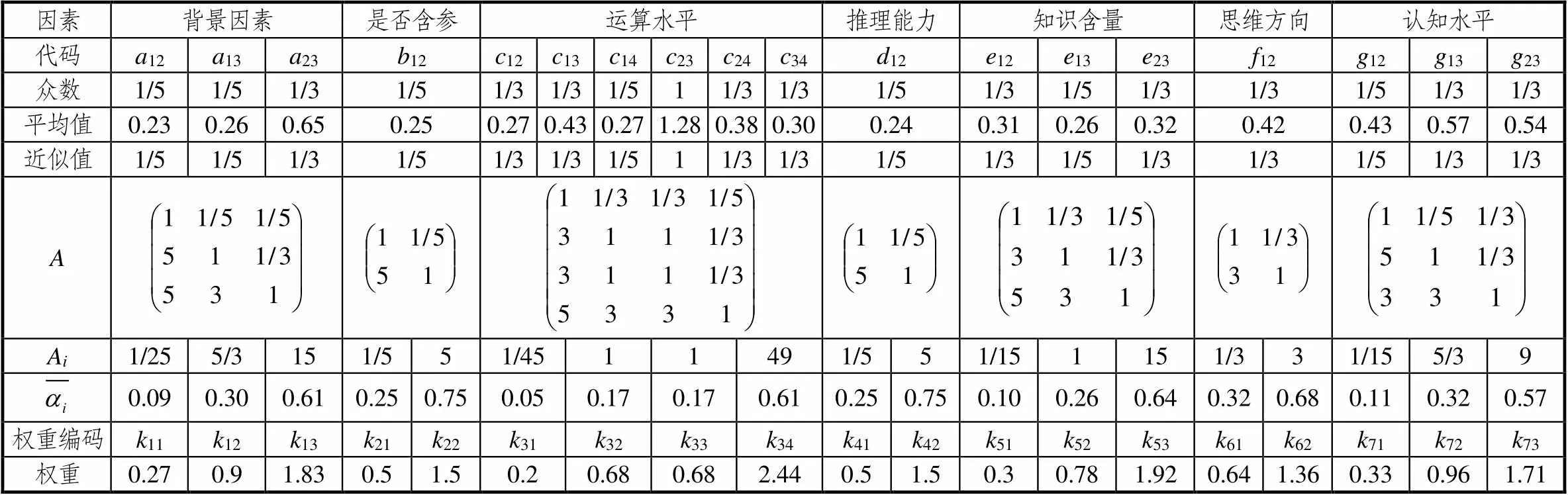
表5 不同水平權重系數計算數據

再依據一致性檢驗指出計算方法得到1=0.008?12，2=0.007?38，3=0.004?09，4=0.000?93，5=0.006?17，6=0.009?01，7=0.003?90．其值均小于0.01的標準，因此，不同水平的權重系數存在較好的一致性．

4 綜合難度系數模型的應用

為了驗證以上建立的綜合難度系數模型的有效性．選取了2019年全國高考理科Ⅰ卷和Ⅱ卷作為分析對象．對試題依據表1的界定，從7個因素共19個水平進行編碼統計．由于考慮到試題分值帶來的影響．編碼過程中將解答題進行分布編碼，即作為兩道獨立的題目編碼兩次，以達到分值的平衡．同時為了檢驗編碼的一致性，編碼采用兩組研究人員分別編碼，編碼一致性為89.17%，再對不一致的編碼項進行討論得到最終編碼結果．

4.1 各因素不同水平對比分析

通過對每個影響因素不同水平編碼數量進行統計，計算在整個測試中的比例，并繪制出圖1的水平對比折線圖．由于“是否含參”這一因素，卷Ⅰ和卷Ⅱ的數據完全一致，因此，這一圖像沒有呈現．

圖1反映了兩個測試在各因素不同水平上考查的對比結果，從圖1中可以看出，除了“是否含參”因素完全保持一致并且有參數和無參數各占一半外，“背景因素”“推理水平”“思維方向”這3個因素也基本保持一致．“背景因素”中無背景的題目占據絕大多數，占整個題目的80%左右，實際生活背景和科學背景的題目很少，僅不到20%．這說明項目考查中情境性很低，沒有將試題融入到具體情境中考查，數學問題的考查僅僅圍繞學科本身，降低了試題的趣味性．現有對核心素養的測評認為，項目的考查需要關注的是課程學習的“真實性學業成就”[21]真實性學業成就不只是習得事實性的學科知識和概念，而是能夠運用這些知識或概念解決復雜的現實性問題[22]．在“推理能力”這一因素中，可以看出簡單推理和復雜推理的比例基本在6∶4，說明試題的考查在注重基本推理的基礎上，保證了復雜推理的考查，因此，也符合選拔性考試的特征．“思維方向”的影響因素中，卷Ⅰ的逆向思維項目略高于卷Ⅱ，逆向思維開始于高級推理，是創新思維的基礎，屬于高階思維水平[23]．可見卷Ⅰ在思維方向難度略高于卷Ⅱ．

圖1 各因素不同水平對比折線圖

在“運算水平”“知識含量”“認知水平”3個因素上，卷Ⅰ和卷Ⅱ有較大的差異．卷Ⅱ的運算水平相對要高于卷Ⅰ，尤其是卷Ⅰ占有較大比例的簡單數值運算，但卻在簡單符號運算方面卷Ⅱ高于卷Ⅰ．運算水平在一定的程度上體現了試卷的復雜程度，尤其是作答需要的時間，在這個方面來看，卷Ⅱ要略高于卷Ⅰ．在“知識含量”因素上，卷Ⅰ在兩個知識點和3個及3個以上知識點的水平上表現出更高的難度，數據均高于卷Ⅰ．但兩個測試項目在知識含量方面多集中在單個知識點的考查，跨章節跨領域知識的考查很少．在“認知水平”因素來看，同樣卷Ⅰ在高認知水平上的比例要大于卷Ⅱ，尤其是在分析層次水平上的項目明顯高于卷Ⅱ．在這一因素上，卷Ⅰ有更高的難度．

4.2 各因素綜合難度分析

利用上述研究獲得的權重系數，將編碼數據帶入公式（1），可以得到各個因素的難度系數．各因素的難度系數得到的雷達圖，如圖2所示．

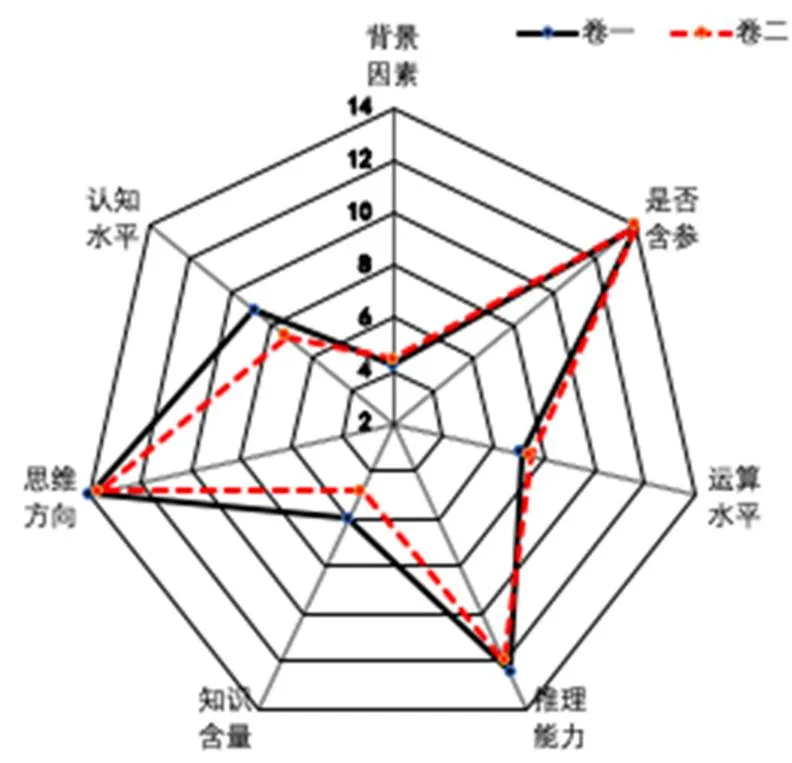
圖2 卷Ⅰ和卷Ⅱ不同因素綜合難度系數雷達圖

圖2在一定程度上反映了整個測試的難度構成，以及不同測試在各因素上的難度差異．從綜合難度系數來分析，整個測試的難度主要集中在“思維方向”“推理能力”“是否含參”這3個因素上．并且這3個因素遠遠高于其它因素．學生要突破難點則需要在思維的靈活性，尤其是逆向思維的培養訓練方面下功夫．教師也應該多關注學生逆向思維的培養．推理能力是數學教育的最核心問題之一，在數學的學習過程中起到至關重要的作用[24]．這一因素成為影響試卷難度的重要部分，是符合數學學科本質特點的．參數作為由“靜態”到“動態”轉變的關鍵指標，對測試難度也起到至關重要的作用．由不含參數到含參數的變化，是由靜態知識向動態能力提升的過程．“背景因素”承載的難度最小，這與高考試題中很少出現實際生活背景和科學背景的原因有直接關系．“認知水平”和“知識含量”的難度系數處于中間地位，在一定的程度上影響了試題的難度．從兩個測試的各難度系數的差異上分析，兩者基本保持難度分布的一致性，僅有個別因素有一定的差異，如在“認知水平”“知識含量”這兩個維度上，卷Ⅰ難度明顯高于卷Ⅱ，在“運算水平”上卷Ⅱ反而要高于卷Ⅰ．但總體來看，卷Ⅰ的各難度系數不同程度的要高于卷Ⅱ．

4.3 測試項目綜合難度系數

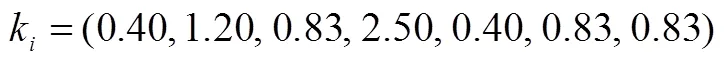
5 討論與展望

5.1 討論

（1）綜合難度系數模型大幅度提升了測試的內容效度和結構效度．

綜合難度系數模型從數學學科特點和影響學生問題解決的因素出發，就測試項目本身進行多維度深層次的分析，并將分析結果通過加權聚類的方式進行量化處理．這一模型打破了只有測試后才能得到試題難度這一壁壘，能夠有效地對測試項目測前預測試題難度．尤其是在大規模和高利害性考試中有重要的作用，由于從7個方面、19個水平對試題做了分析，因此試題在內容上和結構上有了進一步的保障，使得測試更加具有實踐可行性．綜合難度系數模型是將學生問題解決的認知障礙進行量化分析，這種分析過程在幫助教師了解教學重點，幫助學生提升問題解決能力等方面起到了一定的作用．教師通過分析測試考查情況（如對高考試題的分析），可以進一步有針對性地對學生提出補救教學的方案．學生通過對試題的分析和自己的作答結果對比，可以更深層次地進行反思，彌補自己的不足．

（2）綜合難度系數模型對學生的認知診斷測評提供了基本架構．

綜合難度系數模型，有著明顯的結構化特征，可以對測試項目進行較為嚴格的編碼分析．雖然綜合難度系數模型僅僅是對試題的難度做出前期的預測．但如果這種編碼分析和學生的作答建立聯系．其本質上講，綜合難度系數模型的編碼框架就構成了學生測試的認知模型，就可以和認知診斷測評過程進行有效地銜接．認知診斷理論是在項目反應理論的基礎上發展起來的新一代測評理論，它是以項目的形式呈現給反應者任務，把反應者的反應結果作為診斷的數據，反應者的潛在特質作為屬性，將這些屬性表示為潛在變量的變量，再用心理測評模型加以分析，得到認知診斷結果的測評技術[25]．通過綜合難度系數模型的分析，可以將一個傳統的測試改編成一個具有現代測量特征的認知診斷測評，這樣可以依據認知診斷測評的結果對學生做出個性化的補救方案，大幅度提升因材施教的能力．

（3）綜合難度系數模型為測試項目的自動化評判和自適應測評提供了基礎．

從研究分析的過程來看，對于綜合難度系數模型的計算有一定的復雜性，如果僅僅依靠手工計算存在一定的難度，同時也降低了綜合難度系數模型的可操作性和應用價值，因此，可以將綜合難度系數模型的操作過程進行計算機輔助處理，將計算過程程序化．不僅如此，更進一步地，可以將綜合難度系數模型的過程嵌入到計算機自適應測評系統中，達到對測試項目綜合難度分析和自適應測評的雙重目的．現有的學習測評分析工具，可通過學生的在線學習和測評，將結果以可視化形式呈現給學生，幫助學生分析自身學習的問題，促進反思，調整學習策略，以獲得更大進步[26]．學習測評技術自適應性具有傳統測評無法達到的眾多優點，學習測評走向計算機自適應化是測評發展的必然局勢．

5.2 展望

綜合難度系數模型雖在預測測試項目的難度和分析測試內容的量化處理方面有著較大的優勢，但任何測評模型都會存在不同程度的不完善之處，綜合難度系數模型也不例外．因此，要完善綜合難度系數模型還有許多工作可做．首先，雖然對綜合難度系數模型的各個影響因素和不同因素水平的權重進行了計算，較大幅度地提升了綜合難度系數模型的可信度，但是在綜合難度系數模型中對測試難度影響因素的產生僅憑理論分析，還缺乏數據支撐，后期可以通過探索性因子分析和驗證性因子分析對影響因素進行校正，再通過結構方程模型建構測試項目難度影響因素的結構框架，其結果應該會更加合理；其次，綜合難度系數模型的程序化處理和認知診斷測評、計算機自適應測評的結合還會有很多問題有待研究．

[1] 謝維和．教育評價的雙重約束——兼以高考改革為案例[J]．教育研究，2019，40（9）：4–13．

[2] 任子朝，佟威，趙軒．高考試題難度預估的校準與改進研究[J]．數學教育學報，2019，28（6）：1–4．

[3] JOHN W. The greenwood dictionary of education [M]. New York: Greenwood Press, 2003: 130.

[4] 付鈺，張景斌．中美數學教材三角函數習題的比較研究[J]．數學教育學報，2018，27（3）：14–18．

[5] 王建磐，鮑建生．高中數學教材中例題的綜合難度的國際比較[J]．全球教育展望，2014，43（8）：101–110．

[6] 覃淋．“中國大陸”“日本”和“中國臺灣”高中數學教材統計習題難度比較研究[J]．數學教育學報，2019，28（1）：55–60．

[7] 仲扣莊，郭玉英．高中物理課程標準教科書內容難度定量分析——以“量子理論”為例[J]．課程·教材·教法，2010，30（4）：67–71．

[8] 王冰，揭毅．基于綜合難度系數模型的2018年高考地理試題評析[J]．教育測量與評價，2018（12）：40–48．

[9] NOHARA D, GOLDSTEIN A A. A comparison of the national assessment of educational progress (NAEP), the third international mathematics and science study repeat (TIMSS-R), and the program for international student assessment (PISA) [R]. US Department of Education, National Center for Education Statistics (NCES), 2001: 97–110.

[10] 鮑建生．中英兩國初中數學期望課程綜合難度的比較[J]．全球教育展望，2002，31（9）：48–52．

[11] 史寧中，孔凡哲，李淑文．課程難度模型：我國義務教育幾何課程難度的對比[J]．東北師大學報（哲學社會科學版），2005（6）：151–155．

[12] 廖伯琴，左成光，蘇蘊娜．國際中學科學教材實驗內容難度比較——以高中物理為例[J]．全球教育展望，2017，46（4）：23–29，108．

[13] 趙凌云，王秀秀，陳志輝．上海與臺灣初中數學“三角形”內容習題認知難度比較——以滬教版和康軒版為例[J]．數學教育學報，2018，27（5）：66–71，98．

[14] 武小鵬，張怡．中國和韓國高考數學試題綜合難度比較研究[J]．數學教育學報，2018，27（3）：19–24，29．

[15] 張怡，武小鵬．綜合難度系數模型在2016年高考數學試題評價中的應用[J]．教育測量與評價，2016（12）：47–53．

[16] ?SAATY T L. How to make a decision: The analytic hierarchy process [J]. European Journal of Operational Research, 1990, 48 (1): 9–26.

[17] 張怡，武小鵬．基于AHP—模糊矩陣的翻轉課堂綜合評價系統設計[J]．現代遠距離教育，2018（5）：19–26．

[18] 郭亮，鄧朗妮，廖羚．基于Fuzzy-AHP的應用BIM教學評價研究[J]．數學的實踐與認識，2017，47（1）：8–15．

[19] ?CHICLANA F, HERRERA F, HERRERA-VIEDMA E. Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations [J]. Fuzzy Sets and Systems, 1998, 97 (1): 33–48.

[20] 張燕，董玉琦，王煒．基于層次分析法的高中信息技術教師專業知識水平評價——以東北地區為例[J]．中國電化教育，2014（9）：34–39，58．

[21] 楊向東．指向學科核心素養的考試命題[J]．全球教育展望，2018，47（10）：39–51．

[22] ?CHI M T H, FELTOVICH P J, GLASER R. Categorization and representation of physics problems by experts and novices [J]. Cognitive Science, 1981, 5 (2): 121–152.

[23] 王佑鎂．設計型學習：探究性教學新樣式——兼論尼爾森的逆向思維學習過程模型[J]．現代教育技術，2012，22（6）：12–15．

[24] 吳亞萍．美國數學教育的核心問題——推理能力的培養[J]．外國教育資料，1999（5）：59–55．

[25] ?RUPP A A, TEMPLIN J, HENSON R A. Diagnostic measurement: Theory, methods, and applications [M]. New York: Guilford, 2010: 92–125.

[26] 郭炯，鄭曉俊．基于大數據的學習分析研究綜述[J]．中國電化教育，2017（1）：121–130．

The Construction and Application of the Comprehensive Difficulty Model of Mathematical Advanced Examination Questions Based on AHP Theory

WU Xiao-peng1, 2, KONG Qi-ping2

(1. Qiannan Normal University for Nationalities, School of Mathematics and Statistics, Guizhou Qiannan 558000, China; 2. East China Normal University, College of Teacher Education, Shanghai 200062, China)

As China’s national college entrance examination, the difficulty of the test questions directly affected the quality of the test and the fairness of the measurement. The comprehensive difficulty coefficient model could evaluate the overall difficulty of the test questions before the test, providing a guarantee for effective and reasonable measurement. According to the comprehensive difficulty coefficient model, the factors influencing the difficulty of the mathematics college entrance examination test could be divided into seven factors: background, whether or not the test contains parameters, operation level, reasoning ability, knowledge content, thinking direction and cognitive level, and each factor could be divided into different levels. In this study, 16 subject experts were selected to make a comparative evaluation on the difficulty of each dimension of the comprehensive difficulty coefficient. Based on this data, the analytic hierarchy process (AHP) was applied to solve the weights of different factors and weights at different levels in the same dimension, and then a more appropriate and practical comprehensive difficulty coefficient model was established. This model was used to evaluate the national I and national II volumes of science mathematics in 2019, and its application and future research directions were discussed.

analytic hierarchy process; test items; comprehensive difficulty; mathematics college entrance examination; difficulty model

G424.74

A

1004–9894（2020）02–0029–06

2019–12–13

2019年貴州省哲學社會科學規劃青年課題——貴州民族地區高中學生核心素養的認知診斷測評體系構建研究（19GZQN29）；2019年貴州省哲學社會科學聯合基金課題——黔南民族地區高中學生數學核心素養的認知診斷測評研究（LHKT2019YB19）

武小鵬（1986—），男，甘肅天水人，黔南民族師范學院副教授，華東師范大學與美國普渡大學聯合培養博士生，碩士生導師，主要從事數學教育、課堂教學評價、認知診斷測評研究．

武小鵬，孔企平．基于AHP理論的數學高考試題綜合難度模型構建與應用[J]．數學教育學報，2020，29（2）：29?34．

[責任編校：周學智、陳雋]