論數學教育社會學的“理論背景”“體系建構”與“實踐價值”

黃秦安，黃曉林

論數學教育社會學的“理論背景”“體系建構”與“實踐價值”

黃秦安，黃曉林

（陜西師范大學 數學與信息科學學院，陜西 西安 710119）

數學教育社會學在學理上具有跨學科和交叉學科的性質．它受到知識社會學和數學社會學的交互作用和影響．科學知識社會學和數學知識社會學關于科學與數學的認識對數學教育的社會學研究都有很好的啟迪．在借鑒上述兩種知識社會學理論成果的基礎上，作為21世紀以來全球范圍內數學教育研究的一個熱點和重點，探討了數學教育社會學的內涵、層次和基本范疇以及對于中國數學教育實踐的現實意義．

科學知識社會學；數學知識社會學；數學教育社會學；教學實踐

數學知識的性質是怎樣的？這對于數學教育而言是一個同時具有價值論、本體論、認識論和方法論意義的重要問題．因為一門學科的知識本質如何，直接決定了這一學科的課程目標價值、課程內容結構、教育邏輯的建構和教育方式的選擇．科學知識社會學和數學知識社會學作為兩種重要的學術思潮在20世紀末以來風靡國際知識界．那么，科學知識社會學和數學知識社會學對數學教育的理論構思和基本形態究竟有怎樣的啟示？如何在借鑒的基礎上構建數學教育社會學的理論框架？其對于數學教學的價值如何？為了獲得這些問題的回答，首先需要了解科學知識社會學和數學知識社會學的基本觀點．

1 科學社會學視域中的知識意象性

關于知識本質的理解是科學整體觀念的一個有機組成部分．作為科學的社會學向度研究的開創者之一，默頓在1938年的博士論文“十七世紀英國的科學、技術與社會”中，提出了科學作為一個社會系統是有其獨特的價值觀的觀點，并對科學系統進行了功能分析．默頓相信，只有把科學家的科學作為一種演化著的社會組織的行為型式加以研究，才可能更接近于探索科學的本質[1]．知識社會學的另一位代表人物曼海姆強調了知識與社會之間的互動關系，認為知識就其發生學意義而言，不僅取決于人們的社會地位、身份及階級利益，而且根植于特定的文化類型之中．曼海姆提出：“一種具體的知識社會學所面臨的問題是：既定階段的不同群體用什么范疇、什么系統性概念來解釋實際運作中發現的事實？……簡化后的事實就是，不同的知性思潮并不是獨立發展的，而是相互影響、相互充實的，也并非融合進一個共同的體系，而是試圖從各自的一般公理出發來解釋事實的整體．”[2]在研究方法上，曼海姆主張社會科學應具有屬于自己的研究視角和研究方法，認為解釋學是研究社會科學的有效工具，而不必強求使用自然科學方法．

20世紀中葉以來，科學、技術與社會的關系日益成為人們關心的話題．隨著科學研究活動進入國家規模甚至國家集團規模，科學家扮演著越來越重要的社會角色．科學內部的社會關系和社會結構更加復雜，科學成為一種重要的社會建制．1962年，美國科學史家和科學哲學家庫恩出版了著名的《科學革命的結構》一書，其中庫恩論述了科學發展的規律及科學進步與社會發展的關系，提出了“范式”“不可通約性”“科學共同體”等具有高度概括性的科學哲學新概念，并旋即成為許多領域進行研究的認識論與方法論基礎．庫恩還將科學革命與科學共同體的動態過程聯系起來，形成了歷史主義的科學社會學模式[3]．

20世紀70年代初，以愛丁堡學派為代表的科學知識社會學研究（亦稱科學元勘）開始興盛．主要成員有巴恩斯、布魯爾、沙賓和皮克林等．他們提出了系統的關于科學的研究綱領，突破了傳統的對于科學認識的社會學禁區（即僅僅在科學知識的社會生產環境上進行研究），而是把研究的對象直指科學知識的內容本身，并從社會學的視角加以審視，得出了許多極具爭議的研究結果．此學派的思想淵源可直接追溯到維特根斯坦后期哲學，迪爾凱姆、舍勒和曼海姆的知識社會學，庫恩的科學革命理論等．

強綱領的代表作之一是布魯爾的《知識與社會意象》一書．在布魯爾看來，美國默頓學派的科學社會學過于保守，只從宏觀尺度上外在地研究科學與社會的關系，而沒有從社會學角度直接研究科學知識本身即科學的內容．布魯爾倡導對科學知識本身進行社會學分析，結果得到了強綱領的一些基本主張，包括：科學的內容和結果只能根據其地域的歷史和文化的語境來塑造和理解．科學研究的產品，即所謂的自然律，必須始終被視為一種社會建構，其有效性依賴于專家之間的默契．對于科學知識社會學強綱領來說，“所有的事實都是‘社會性建構起來的’，科學理論不過是各種‘神話’或‘敘事’，科學爭論最終可以借助‘修辭學’或‘結成同盟’得到解決，真理僅僅是主體之間的相互一致的見解”[4]．美國著名科學社會學家科爾曾概括了哲學上的社會建構主義（即科學知識社會學）的幾個基本假定：“首先，他們認為科學不是一個由規則支配的活動，科學并不遵循一套能引導科學工作者獨立發現真理的程序．第二，他們認為科學爭論并非總能由經驗證據來裁決……第三，也是最重要的一點，他們在哲學上采取了相對主義的立場，否認自然界作為客觀外界的重要性，否認自然界對科學知識的內容有重要作用．”[5]依照上述假定，科學家的社會行為就成了科學思想最重要的決定因素．

但強綱領的認識偏差也是需要指出的．這種偏差的主要表現是其忽視或無視知識的客觀性和非社會性的一面．后來，即使是從事科學元勘的研究者也開始意識到SSK的這一缺陷．1992年皮克林出版《作為實踐和文化的科學》，試圖實質性推進SSK的發展．他特別強調實踐和文化的重要性，認為對于理解完整科學實踐和科學文化而言，要考慮許多因素，這其中包括社會因素和非社會因素，但現在不應再強調社會因素的優先地位．社會因素在強綱領中的地位開始被弱化．由此，科學知識社會學進入后SSK時期．

2 數學知識社會學：從柏拉圖主義到社會建構主義

總體上看，科學知識社會學的基本立場、觀點與方法對于數學知識社會學的建構都有很重要的借鑒價值，這是由數學知識與科學知識之間的普遍性和公有性所決定的．就學科的共性而言，科學知識社會學關于科學的一般認識也是適用于數學的．從數學知識的建構過程看，社會、文化、歷史因素無疑都會對數學的發展有一定的影響．因為數學共同體的成員，都是社會的一分子，都要把它所處時代的各種觀念、價值判斷帶到數學研究中去，同時又都被時代文化和社會環境所塑造．這種交互性會貫穿數學知識發展的始終．從數學研究對象看，除了自然現象之外，社會現象中也有數學的規律、結構和關系可循．而在各種社會現象中，人是最活躍和極為重要的因素，所以無論是從數學知識生產的內部和外部看，某些數學知識有一定的主觀建構色彩是不可避免的，但這并不意味著數學知識就是一種完全意義上的社會建構．

與一般的科學社會學研究模式相比，數學社會學或數學知識社會學除了要考慮數學作為一門科學的一般性問題之外，還要特別關心數學與其它科學之間的社會性互動關系，尤其是要關心在數學內部的各種社會性因素之間的相互關系與相互作用．在西方，數學知識社會學研究的代表人物有曼海姆、布魯爾、歐內斯特和雷曼等．在曼海姆看來，“數學就是‘如此這般的真理’（truth as such）．數學和邏輯都被看作是以自身所是的方式存在的真理實體，它們獨立于任何相信或知道它們的人．按照這種觀點，即使沒有人類，數學真理仍然是真的”[6]．可見，雖然曼海姆是一位著名的知識社會學家，但卻持有一種柏拉圖主義的數學觀．而布魯爾對上述實在論的解釋自然是不認可的．“實在論者假定存在著一些邏輯和算術的原型對應著數列的真實連續．這種原型對于人的世界是沒有用的，除非它能與人相聯系．”[6]可見，布魯爾關于數學知識具有社會學的基本觀點是與曼海姆的見解直接相對立的．沒有對于柏拉圖主義和實在論的數學觀的反對，數學知識社會學的基本理論就無法建立起來．

英國數學哲學家歐內斯特是作為一種數學哲學的社會建構主義的堅定倡導者和維護者．歐內斯特曾明確表達了其思想來源和知識基礎：“社會建構主義視數學為一種社會建構．它吸收約定主義之思想，接受了人類知識、規則和約定對數學真理的確定和判定起著關鍵作用．它采納擬經驗主義之易繆主義認識論，包括數學知識和概念是發展和變化的觀點．它還采用了拉卡托斯的哲學論點，即按照數學發現的邏輯，數學知識在猜想和反駁中得以增長．相對于規定性哲學來說，社會建構主義是一種描述性的數學哲學，旨在以合適的標準對廣義理解的數學本質予以解釋．”[7]歐內斯特指出：“所有的數學知識都是在文本和個人知識中被表達的，客觀的數學知識是在數學的文化和公共機構中通過這些文本和個人的相互關系和相互作用被社會地發現的．”[8]與此相似，戴維斯、赫斯、基切爾和拉托爾都表達了“社會文本和專業的數學共同體在數學知識的創造和辯護方面扮演的核心作用”[9]．

在1989年發表的“建構主義，數學與數學教育”一文中，雷曼持有一種直覺主義的建構主義立場：“建構主義作為一種可以選擇的范式，對于數學教育具有豐富和重要的意義．”[10]到了20世紀90年代之后，雷曼特別強調了在數學學習中的“主體間性”，并將其視為對極端建構主義者（radical constructivist）范式的一種挑戰．雷曼主張，極端建構主義應走向社會建構主義并與主體間性相結合．而皮亞杰的個體建構理論與維果斯基的社會建構的對比則顯示出極端建構主義對兒童學習數學解釋力的不足[11]．由于上述幾位代表人物及其理論觀點，數學教育的社會學研究被逐步認可并得以發展．

進入新世紀以來，中國學者開始逐步關注數學知識社會學的發展動態和理論建構問題．著名數學教育家鄭毓信教授是這一研究群體中的主要代表人物．在一系列著作和文章中，鄭毓信教授都對國際數學知識社會學的理論成果予以評介和反思，并結合中國數學教育的實際，創造性地開創了中國特色數學教育社會學的研究范式．

從上述系列介紹可以看到，通過對數學知識發生過程的社會學描述，數學知識社會學既有外部的、廣泛的社會意義，也有內部本身具有的社會意義，由于在第一種意義上數學與其它科學的外部社會意義基本相同，因此主要把研究的側重點放在第二種意義，即數學內部的社會意義上．

3 數學教育社會學的內涵與層次及基本范疇

數學教育社會研究的兩個重要理論背景是科學知識社會學和數學知識社會學．特別是20世紀90年代以來，“數學社會學成為數學教育和數學哲學話題的核心成分”[12]．這與社會建構主義思想在數學教育領域的興盛具有內在的關聯性．從普遍性來看，數學教育社會學的一個基本立場就是，在任何情況下數學知識的學習都不可能離開特定時代的社會條件和社會關系的總和．科學知識社會學和數學知識社會學的基本觀點對于數學教育的社會學研究具有很好的借鑒價值．但數學教育社會學卻不能簡單地看作是把科學知識社會學和數學知識社會學的基本觀點平移或擴大到數學教育領域，而是要在借鑒的基礎上，重點考量數學教育的獨特規律性，構建能夠體現數學知識本質和數學教育本質的基本理論體系．

歸納起來，數學教育社會學可以定義為采用科學知識社會學和數學知識社會學的理論視角，結合教育社會學和知識社會學的研究方法，對數學教育的研究對象、學科特征、教育目標、過程、行為與方式進行多角度分析的一門跨學科研究．

在數學教育過程中，在形式上，社會性概念主要可以劃分為3個層次：一是與教育概念相對應的“大社會”（即整體社會環境）概念．在這個層次上，社會性是指教育之外，特別是學校教育之外的整個人類意識、觀念和行為．在這個層面上，社會性對整個教育和所有學科的教育都有交互影響．例如，不同國家、民族或種族由于信仰、價值觀、國家或民族意識的不同，對于數學教育的認識也都不盡相同．這樣，關于數學教育，就必然會有差異性和多樣性的認知．而在這樣一個范圍內的數學教育社會學研究領域是十分寬闊的．二是在教育內部的社會概念．介于大社會與數學教育內部之間的、與一般教育共享的社會性概念（包括一般教育的社會性原理、實踐和其它學科的社會性教育方式）及其對于數學教育的交互作用．第三個層面是數學教育內部的社會性．在數學教育過程中所展現的具有社會性意義的現象．包括教師和學生以及一切具有主體性地位的參與者．在數學教育過程中的角色關系與轉換、信息傳播方式和相互關聯．在數學教育內部，社會學研究的意義與數學知識和數學學科的特點緊密相關，因此，數學知識社會學中相當一部分含義可以延伸至數學教育社會學當中．

從上述3個層次看，數學教育的社會意義都是十分豐富的．這3個層次之間并不是截然分離的，而是相互關聯的．因此，第一和第二個層次上的社會學含義也并不被排斥在數學教育社會學的研究范疇之外．例如，跨文化視野、基于人類學視域乃至于政治學視角的數學教育研究都是在國際數學教育研究中富有特色且取得了相當研究成果的．如埃奇克對國際視野下性別與數學教育的回顧[13]；中國香港的梁貫成對中國文化、伊斯蘭文化與數學教育的研究[14]；巴頓對數學與數學教育中人類學視角的研究[15]；瓦萊羅關于數學教育的社會政治視角的研究等[16]．

與數學知識發生學的角度相比，在數學教育中的社會關系與結構比單純的知識建構要更為多樣和復雜．因為它包含了更為多樣的社會對象與社會關系（人與人、人與學校、人與家庭、人與團體、人與教育媒體等），因此數學教育社會學具有比數學知識社會學更為豐富多樣的社會學內涵和層次．

數學教育的社會研究是近數十年來國際數學教育的一個重要領域．20世紀90年代以來，“數學社會學成為數學教育和數學哲學話題的核心成分”[17]．在2013年出版，由5位國際數學教育著名學者主編的《國際數學教育手冊（3）》中，對數學教育的社會、政治和文化維度的探討位居4個主題之首．這也充分表明了數學教育的社會研究在近年來國際數學教育研究中的重要地位．該手冊的主編之一克萊門茨在該書的導言中說：“在過去十年里有一些最主要的發展．其中第一個就是與雷曼稱之為數學教育的社會轉向相關的．許多學者都把注意力投向了社會文化理論在這一領域日益增長的應用．”[18]

如果僅僅把數學教育社會學研究停留在一般的平行照搬科學知識社會研究的水平和層次上，就不能完全揭示數學教育社會學的本質屬性．為了避免簡單的類比，還要特別注意數學知識的獨特性與數學教育的獨特性．在數學教育中，主要是數學思維、數學理解與數學學習的個體性（個性化）與數學交流的公共性之間的關系．具體表現為主觀知識與客觀知識、個體知識與社會知識、主體性與主體間性、LMD（數學發現的邏輯）與GLMD（數學發現的辯證邏輯）以及修辭與隱喻與邏輯與演繹之間的相互轉化、交互解釋等．具體見圖1．

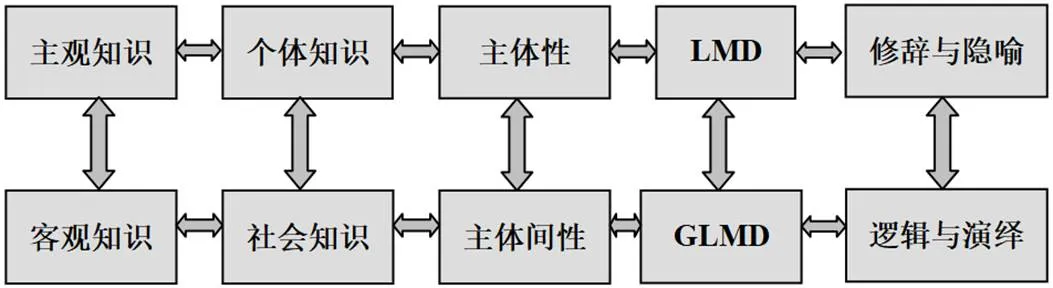
圖1 數學教育社會學的基本范疇

就圖1中的“主觀知識和客觀知識”以及“個體知識和社會知識”這兩組緊密相關但又有各自側重點的范疇而言，在傳統的數學觀和數學教育觀念中，數學主觀知識和個體知識都沒有被賦予足夠的價值應然．而數學知識社會學特別突出了數學知識建構過程中的社會學色彩，這就使得主觀知識和個體知識被放在教學共同體結構中一個同樣重要的位置上．從辯證關系看，由于客觀知識的社會化要求，個體知識的主觀建構并不是隨心所欲的．客觀性的要求對個體的認知有強烈的導向和調節作用．這種引導和調節就是個體認識行為應該尋求一個社會性的尺度，遵循一個相對合理的、被教學共同體和學習共同體所認可的標準．這樣，由于客觀性和共同性的知識展示，就把那種僅僅受制于個體思維中的對于一切事物的初級的、樸素的、重復甚至浪費和無效的認識給過濾掉了，使得個體的認識站在了較高的平臺上，因而也就使得在社會情境中個體的思維具有了更為經濟、更為集中和更為超前的特征．

4 數學教育社會學研究的學理視閾與現實意義

由于多年以來數學教學中功利主義和應試文化色彩日益濃厚且相當固化，數學課程實踐者的主流意識和主要目標被應試需求所異化并強化，致使師生關系沒有很好地體現良好的主體間性，課堂教學目標和教學互動方式單一，教師權威壓抑了學生的主體創新意識，追求標準解法和答案成為教學的導向，素質教育流于口頭形式化甚至虛無化．數學教學與人生教育和生命體驗相互脫節，教育觀念游離于當代主流教育思想之外．教學模式有千人一面、雷同化和趨同化趨勢．

上述問題雖是數學教育難疾，但并非積重難返，需要從多個系統化的維度逐步加以解決．從數學教育社會學的視閾看，一個有力的切入點是對師生關系的核心結構——教學共同體予以特別的關注．數學教學應充分展示教學雙主體性并培育良好的師生主體間性．教師和學生作為不同的教學主體，其相互關系稱為主體間性．基于文化和話語心理學的透視，雷曼以語言和話語實踐為中心視角，把學習看作是進入社會實踐的一種啟蒙．而參與文化實踐時的知識都是以一種學習的認識論原理存在的．諸如課堂中的社會關系，數學語言、意義、聯結、策略和人工制品等．雷曼提出了“學習數學或學會數學地思考就是學會數學地表述”的重要觀點[19]．

在當下中國的數學課堂實踐中，占據主角的師生教學共同體模式中存在著很大的缺陷．比如教師單邊的話語權和主導性過大，而學生方則缺乏積極性、選擇性和主動性，致使主體間性長期偏態，非常不利于學習者數學文化主體地位的確立、培育和發展．從學習心理學的角度看，數學課堂要重視高效、優質和良性的教學文化與學習共同體的營造并納入其課堂實踐．比如，傳統數學教學鼓勵獨立思考，雖然仍然是極富價值的，但在現代教育文化觀念中，更加強調的是在教學與學習共同體中把培育合作意識和團隊精神作為數學教學的一個重要目標．

在當代數學與科學的前沿研究中，團隊合作和協作已成為一種基本模式．例如1979年，由一個數學家小組做出的有限單群分類的證明，相關結果收集起來，累計有一萬頁之多．其中許多結果依賴于計算機的工作．很難有單個數學家能把所有的證明過程逐一檢驗，這時，對其他數學工作者的信賴就變得十分重要．再比如，20世紀90年代，英國數學家懷爾斯（Wiles）給出了費馬大定理的一個復雜證明．一開始，證明中的一個錯誤被懷爾斯本人發現．后來，他的新證明被一個由12名專家組成的小組所審查．而“大多數數學家并沒有跟蹤懷爾斯證明中的細節，只是由于社會學的確認而表達了信任”[20]．鑒于合作在數學創造中日益增長的趨勢，有學者指出：“數學家在創造數學的過程中相互之間的合作交流極大地有利于其數學創造，因而數學家應該積極地尋找機會和其他的數學家進行合作交流．”[21]這一建議同樣適用于數學教學活動．在數學教育中，科學知識學習過程中學習者社會性角色的扮演應該成為科學教育的一個子目標．具體來看，與他人相互溝通、協調和分工協作，理解他人的想法和意圖，培養彼此的信任感，體味學習活動和科學探究活動中的社會角色．合作學習、研究性學習就是這樣一些有效促進學習共同體效率的方式．

在中國已經開展多年的大學生數學建模競賽是一個較為成功地展現數學教育社會學價值的范例．大學生數學競賽設置了學生從未接觸過的實際問題，允許學生以研究小組的形式在教師指導下進行探索攻關，競賽對解決方法也不設立任何限制．“學生可以運用自己認為合適的任何數學方法和計算機技術加以分析、解決，他們必須充分發揮創造力和想象力，從而培養學生的創新意識及主動學習、獨立研究的能力．競賽沒有事先設定的標準答案，但留有充分余地供參賽者發揮其聰明才智和創造精神．”[22]以接近于真實的數學共同體研究形式所開展的數學探究與學習活動，可以成為培養大學生科學研究基本能力（如問題意識，技術路線與攻關方案的抉擇、論證與評估，團隊精神等）的有效方式．

在基礎教育領域，隨著數學課程改革的諸多細化和深化，數學教學中的教育社會學維度受到了越來越多教師和研究者的關注．合作學習和分組學習等多種學習共同體方式越來越頻繁地出現在實際教學活動中．在社會建構主義、社會交往理論、數學知識社會學等理論的引領下，師生的主體性和主體間性等社會性教學觀念和空間獲得了極大的強化和拓展．一些焦點、難點和有挑戰性的相關話題（其中許多都涉及到教學共同體和學習共同體的構建），如數學教科書的社會學分析、數學教育中的機會平等問題、信息技術和高技術（如學習機和人工智能）的發展對數學教育中主體性地位的挑戰、數學教育的人文價值、數學教育中的性別差異問題、數學教育中的精英教育與大眾教育、數學教育中的學困生問題、民族數學教育和特殊人群的數學教育問題等都開始被數學教育界留意并開始了或初步或深入的探討．

概括起來看，數學教育的社會學研究，是數學教育專業化和多元化發展的一個重要方向和必然趨勢．許多原發性的、深層次和重要的數學教育理論與實踐問題，只有深入到社會學層面上，才可以獲得更好的探討、理解、解釋和解決．從多學科、跨學科和交叉學科的視角探索數學教育社會學，是一個可以選擇的理論路徑．許多與人類社會學、人類文化學、民族文化、語言學、比較教育學等學科相關的數學教育研究都有很好的研究前景．進而，如何讓數學教育社會學的理論研究成果為更多的研究者所熟悉，為一線教師服務，成為可操作的教育手段和教學指導，就成為需要進一步探索的數學教育實踐課題．

[1] 默頓．十七世紀英國的科學、技術與社會[M]．范岱年，吳忠，蔣效東，譯．成都：四川人民出版社，1986：2．

[2] 曼海姆．卡爾·曼海姆精粹[M]．徐彬，譯．南京：南京大學出版社，2005：15．

[3] 庫恩．科學革命的結構[M]．金吾倫，胡新和，譯．北京：北京大學出版社，2012：36．

[4] 索卡爾，德里達，羅蒂，等．“索卡爾事件”與科學大戰——后現代視野中的科學與人文的沖突[M]．蔡仲，邢冬梅，等譯．南京：南京大學出版社，2002：65．

[5] 史蒂芬·科爾．科學的制造[M]．林建成，王毅，譯．上海：上海人民出版社，2001：6．

[6] BLOOR D. Wittgenstein and Mannheim on the sociology of mathematics [J]. Studies in the History and Philosophy of Science, 1973 (4): 173–191.

[7] ERNEST P. The philosophy of mathematics education [M]. London: Falmer Press, 1991: 42.

[8] ERNEST P. Social constructivism as a philosophy of mathematics [M]. New York: State University of New York Press, 1998: 244.

[9] ERNEST P. Forms of knowledge in mathematics and mathematics education: Philosophical and rhetorical perspectives [J]. Educational Studies in Mathematics, 1999, 38 (1–3): 67–83.

[10] ?LERMAN S. Constructivism, mathematics and mathematics education [J]. Educational Studies in Mathematics, 1989, 20 (2): 211–223.

[11] ?LERMAN S. Intersubjectivity in mathematics learning: A challenge to the radical constructivist paradigm [J]. Journal for Research in Mathematics Education, 1996, 27 (2): 133–150.

[12] ?RESTIVO S, BAUCHSPIES W K. The will to mathematics: Minds, morals, and numbers [J]. Foundations of Science, 2006, 11 (1–2): 197–215.

[13] ?ERCHICK D B. A review of international perspectives on gender and mathematics education: It really is about gender [J]. ZDM, 2011, 43 (6–7): 1?021–1?024.

[14] ?BISHOP A J. Critical issues in mathematics education [M]. New York: Springer, 2008: 135–147.

[15] ?BISHOP A J. International handbook of mathematics education [M]. Dordrecht: Springer, 1996: 1?035–1?053.

[16] ?VALERO P. Socio-political perspectives on mathematics education [J]. Mathematics Education Library, 2004 (35): 5–23.

[17] CHEVALLARD Y. On mathematics education and culture: Critical afterthoughts [J]. Educational Studies in Mathematics, 1990, 21 (1): 3–27.

[18] ?CLEMENTS M A, BISHOP A J, KEITEL C, et al. Third international handbook of mathematics education [M]. New York: Springer, 2013: vii.

[19] ?LERMAN S. Cultural, discursive psychology: A sociocultural approach to studying the teaching and learning of mathematics [J]. Educational Studies in Mathematics, 2001, 46 (1–3): 87–113.

[20] ?BARENDREGT H, WIEDIJK F. The challenge of computer mathematics [J]. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 2005, 363 (1?835): 2?351–2?375.

[21] 張曉貴．對數學家數學創造過程的社會思考[J]．自然辯證法研究，2010，26（7）：85–88．

[22] 謝金星．科學組織大學生數學建模競賽 促進創新人才培養和數學教育改革[J]．中國大學教育，2009（2）：8–11．

Sociology of Mathematics Education: The Theoretical Background, System Construction and Its Value of Teaching Practice

HUANG Qin-an, HUANG Xiao-lin

(School of Mathematics, Shaanxi Normal University, Shaanxi Xi’an 710119, China)

The Sociology of Mathematics Education (SME) has the nature of cross-subject and interdiscipline in scientific principle. It was subjected to the interaction of Sociology of Education, Sociology of Knowledge, Sociology of Mathematics simultaneously. The study of Sociology of Scientific Knowledge and the study of Sociology of Mathematical Knowledge have certain enlightenment towards mathematics education. Using for reference the theoretical production of SSK and SMK, The Sociology of Mathematics Education can show their characteristics by breakthrough the research boundary of above two research views. As a key field of global mathematics education research, it is important to inquire the connotation, hierarchy and basic category of SME and to indicate the guiding significance of get rid of realistic difficulties of Chinese mathematics education.

sociology of scientific knowledge; sociology of mathematical knowledge; sociology of mathematics education; teaching practice

G40–03

A

1004–9894（2020）02–0001–05

2020–01–10

國家哲學社會科學基金2017年度教育學重點招標項目——教師核心素養和能力建設研究（AFA170008）

黃秦安（1962—），男，陜西西安人，教授，博士生導師，主要從事數學教育、數學哲學和數學文化研究．

黃秦安，黃曉林．論數學教育社會學的“理論背景”“體系建構”與“實踐價值”[J]．數學教育學報，2020，29（2）：1-5．

[責任編校：周學智、陳漢君]