鋼絲繩隔振器的力學性能研究綜述

張春輝，盧凱田,，張 磊，閆 明

(1.海軍研究院, 北京 100161；2.沈陽工業大學 機械工程學院, 沈陽 110870)

鋼絲繩隔振器作為被動隔振技術[1]的一種代表，其具有異于其他非線性器材的優良性能，如固有頻率低，對低頻和高頻干擾[2]均有良好的隔振作用；在沖擊載荷作用下剛度軟化，能夠有效隔離沖擊；此外，還具有耐高、低溫等優點，被廣泛的運用到建筑設備、高壓設備、氣體絕緣變電站、抗震改造斷路器、地震隔離設備、衛星運載、艦載等電子、機械設備與儀器儀表的隔振緩沖中[3-4]。國內外學者對鋼絲繩隔振器進行了大量的試驗研究，獲得了鋼絲繩隔振器直徑、股數、纏繞方式和尺寸對鋼絲繩隔振器剛度和阻尼特性的影響。由于鋼絲繩隔振器具有突出的結構非線性、幾何非線性、材料非線性等因素[5]，以及明顯的遲滯效應，因此，對其非線性的理論分析是研究的重點。

本文從鋼絲繩隔振器的結構上介紹了現在常用的五種鋼絲繩隔振器，在非線性動力學中重點分析了四種常用的力-位移遲滯模型，在此基礎上，通過準靜態、振動和沖擊試驗研究鋼絲繩隔振器的力學特性，以期在保證鋼絲繩隔振器隔振能力的基礎上，提高其隔沖能力，并對待進一步解決的問題以及將來的研究方向進行了討論與展望。

1 鋼絲繩隔振器的分類

1)T型鋼絲繩隔振器

T型結構的鋼絲繩隔振器也稱為條形鋼絲繩隔振器，主要是由一根鋼絲繩纏繞固定在夾板之間，目前應用最多。但此種結構的鋼絲繩隔振器在側掛時容易產生較大變形影響其隔振性能。T型鋼絲繩隔振器隔振性能主要由鋼絲繩直徑、線圈數目、纏繞螺旋傾斜角決定，其結構參數對剛度、阻尼特性有很大影響[6]。常見的T型鋼絲繩隔振器結構如圖1所示：其中圖1(a)是常用的的T型鋼絲繩隔振器，圖1(b)具有限位裝置，適用于有位移要求的設備。

圖1 T型鋼絲繩隔振器

2)G型鋼絲繩隔振器

G型鋼絲繩隔振器由于隔振器呈拱形結構，故又稱之為拱形鋼絲繩隔振器。與T型鋼絲繩隔振器相比，其橫向、縱向、垂向的剛度比接近1∶1∶1，拱形結構穩定性更優，G型鋼絲繩隔振器如圖2。

圖2 G型鋼絲繩隔振器

3)Q型鋼絲繩隔振器

Q型鋼絲繩隔振器其鋼絲繩纏繞在兩圓形夾板之間，由于整個隔振器呈球形結構，故稱之為球形鋼絲繩隔振器。如圖3所示：該隔振器夾板為圓形，比T型隔振器穩定性好。

4)D型鋼絲繩隔振器

D型鋼絲繩隔振器又稱碟型鋼絲繩隔振器，其結構簡單，重量輕、體積小，上下單孔安裝，安裝使用中通過多種設置方法可以吸收上下、左右、前后三維的振動和沖擊，適用于飛行器、攝像設備減振，如圖4所示。

圖3 Q型鋼絲繩隔振器 圖4 D型鋼絲繩隔振器

5)環形單元鋼絲繩隔振器

環形單元鋼絲繩隔振器的彈性阻尼元件是多個相互獨立的鋼絲繩圈[7]，通過選用一定個數的繩圈組成如圖5所示的環形鋼絲繩隔振器。該隔振器繩圈安裝便捷，通過改變線圈數目調整隔振器的剛度和阻尼。環形鋼絲繩彈性元件可以由不同直徑的鋼絲繩做成，相同尺寸的繩圈可以組合安裝。由于多個線圈并聯安裝，因此研究幾何參數對單個鋼絲繩圈性能的影響就可以得到整個鋼絲繩隔振器的剛度特性[8]。

圖5 環形單元鋼絲繩隔振器

除了以上5種主要形式外，還有其他結構形式的鋼絲繩隔振器，比如鋼絲繩管道阻尼隔振器、柱形鋼絲繩隔振器以及與橡膠復合的鋼絲繩隔振器等。

在實際應用中鋼絲繩隔振器會產生失效現象，如圖6所示，研究發現鋼絲繩隔振器多是拉伸斷裂，壓縮時隔振隔沖性能較好，可以通過設計一種新型的可雙向壓縮鋼絲繩隔振器改善其拉伸性能。

圖6 鋼絲繩隔振器失效圖

2 鋼絲繩隔振器的非線性力學特性

鋼絲繩隔振器作為優異的非線性隔振器材，其隔振原理是鋼絲繩絲與絲、股與股之間相對滑移從而產生干摩擦并消耗大量的能量。基于干摩擦的產生過程，建立鋼絲繩隔振器的力學模型。通過對鋼絲繩隔振器的力-位移曲線進行研究，發現鋼絲繩隔振器有明顯的遲滯現象，用數學方程建立鋼絲繩隔振器遲滯力學模型。

2.1 干摩擦阻尼的性質

機械系統中的摩擦主要有庫倫摩擦、粘性摩擦和stribeck摩擦。庫倫摩擦切向力正比于法向力，其摩擦系數與接觸面積無關[9]。白亮亮對機械系統進行無量綱化處理發現激勵頻率影響振幅，軌跡的形態與摩擦力有一定的關系[10]。激勵頻率變大鋼絲繩隔振器的共振值反而減小，能夠明顯的改善隔振性能。研究發現干摩擦力滯后于鋼絲繩絲與絲、股與股之間的相對滑移，隨著位移的增加，干摩擦力逐漸增大。鋼絲繩隔振器的力與位移所圍成的封閉曲線代表了所消耗的能量。

李守昆將[11]干摩擦阻尼展開成傅立葉級數，將遲滯部分的阻尼和等效阻尼中的彈性力部分分開表達，從而建立了干摩擦阻尼的遲滯模型。

2.2 鋼絲繩隔振器的動態遲滯力學模型

鋼絲繩隔振器的結構多種多樣，但其力學特性可以通過遲滯特性力學模型來描述。鋼絲繩隔振器的力學性能主要包括剛度和阻尼性能，它們反映了力與位移、力與速度之間的關系，對于線性隔振器，作用力和位移呈線性關系，其剛度特性和阻尼特性比較簡單，用試驗即可測定，可得到較準確的數學模型；而非線性隔振器作用力和位移關系不可以用簡單的線性函數來表示，其剛度和阻尼特性呈非線性，對其遲滯特性力學模型的建立是動力學研究領域研究的重點[12]。學者們從理論和試驗兩個方面探究非線性隔振器的數學模型。

鋼絲繩隔振器是一種非常實用的隔振器材，其非線性遲滯特性決定了它的隔振性能，其遲滯回線與非線性軟彈簧系統有很大不同，其模型主要為Bouc-Wen模型、雙線性模型、跡法模型和多項式模型[13]。

1)Bouc-Wen模型

Bouc-Wen模型最初是由Bouc在研究遲滯系統的周期運動的時候提出的，后由Wen等學者不斷改進而最終形成[14]，其數學描述如式：

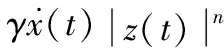
(1)

其中：z(t)表示遲滯恢復力;α、β、γ和n是遲滯環參數，它們控制遲滯環的形狀和大小；α，β和n是正實數；γ是實數。Bouc-Wen模型中包括四個參數，他們對遲滯環的形狀有很大的影響。

Bouc-Wen模型的力—位移關系通過一階線性方程來描述，遲滯環的切線即為鋼絲繩隔振器的剛度，遲滯環的切線表達式即為剛度的表達式，改進的Bouc-Wen模型[15]更適合非線性的表達。

2)雙線性模型

Bouc等提出的有非線性微分方程控制的光滑滯回模型通過設置不同的模型參數來描述不同的非線性隔振器的力學特性。在實際應用中，可以采用與實際情況更符合的雙線性遲滯模型[16]來描述，雙線性遲滯模型可以更好的表達非線性性能。雙線性遲滯模型如圖7所示。

圖7 雙線性遲滯模型

圖7中，K1為隔振器在臨界滑移力之前的剛度，K2為鋼絲繩在臨界滑移力之后的剛度，Py為臨界滑移力。這種特性表明，當承載小于Py時，它有較大的剛度K1，這時鋼絲繩股間沒有滑動，整個鋼絲繩構成完整的彈性體；當承載大于Py時，鋼絲相對滑動而軟化，因此剛度降低為K2，載荷降低時剛度又增大為K1，加載和卸載遲滯曲線為一密閉曲線，從而耗能并產生了遲滯阻尼。

雙線性模型通過臨界滑移力對遲滯曲線進行兩階段處理，考慮了鋼絲繩隔振器的壓縮剛度軟化特性，但滯回曲線表明隔振器拉伸時剛度硬化，雙線性模型不能準確描述鋼絲繩隔振器拉伸和壓縮方向不對稱的遲滯特性。

3)跡法模型

Badrakhan在Bouc-Wen模型的基礎上建立了跡法模型[17]，其數學表達式為：

(2)

跡法模型運用的主要理論為平均原理和等效原理[18]，其模型表達方式很多。遲滯恢復力F為非線性彈性恢復力Fe與阻尼力Fc之和，振幅和頻率是決定力大小的兩個因素，其表達式為：F=Fe+Fc

(3)

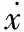
跡法模型根據不同的研究對象有不同的表達式。Cutchins[19]等通過振動試驗，運用多庫侖阻尼模型來分析鋼絲繩隔振器的剛度和阻尼特性。Tinker[20]等提出用與速度相關的多次方粘滯阻尼描述，實驗表明，速度對隔振器的遲滯特性影響較小。付永輝[21]通過多項式描述跡法模型恢復力，小振幅時擬合度較好，振幅較大時不能準確描述其遲滯特性。

4)多項式模型

龔憲生等用與振幅和頻率相關的多項式模型來體現鋼絲繩隔振器的剛度和阻尼特性[22]。將鋼絲繩隔振器的遲滯曲線分別用剛度曲線和多項式阻尼曲線來描述，剛度函數、多項式阻尼函數和與阻尼相關的函數改變遲滯回線的形狀。此種方法能識別出阻尼成分中的粘性阻尼、干摩擦阻尼和高階阻尼的比值。聞邦椿院士稱之為“多項式模型”[23]，該模型適用于描述對稱的力-位移曲線，不能準確描述鋼絲繩隔振器拉壓時的非對稱力-位移曲線。

當前應用最廣泛的是Bouc-Wen模型和雙線性模型，這兩種模型相比跡法模型和多項式模型能夠較準確描述鋼絲繩隔振器的力-位移曲線。Bouc-Wen模型和雙線性模型現多用于描述鋼絲繩隔振器準靜態和振動時的力學特性，沖擊時的力學特性與準靜態和振動的力學特性之間的關系還需進一步的研究。同時，鋼絲繩隔振器拉伸時剛度硬化，壓縮時剛度軟化，應將拉伸和壓縮分開考慮，建立更符合實際的遲滯力學模型。

3 鋼絲繩隔振器的力學性能試驗研究

鋼絲繩隔振器以其結構簡單、安裝方便、重量輕等特點，以及優越的隔振性能，已經越來越廣泛的被應用到機械、交通、航空、船舶和建筑領域。隨著技術的發展，對于鋼絲繩隔振器的非線性性能的研究和模擬分析的技術也在不斷的深入和發展，一些學者們進行了大量的試驗研究，包括靜態試驗、振動試驗和沖擊試驗。

1)在靜態試驗中，劉廣璞[24]對鋼絲繩隔振器進行加載和卸載變形試驗，結果表明遲滯曲線面積大較線性元件能夠吸收更多的沖擊能量。班書昊[25]對鋼絲繩隔振器的靜態加載試驗表明壓縮狀態下垂向呈軟化特性，橫向和縱向呈硬非線性特性，并且近似滿足線性剛度之比k橫向∶k縱向∶k垂向=1∶1∶3，但沒有研究拉伸時鋼絲繩隔振器遲滯特性。其垂向拉壓試驗表明壓縮時剛度軟化，拉伸時剛度硬化。壓縮剛度的軟化是由于鋼絲之間出現較大滑移所致;拉伸時向直鋼絲繩拉伸狀態過渡剛度有漸硬趨勢。萬葉青[26]通過電液伺服液壓試驗臺測得鋼絲繩隔振器的遲滯曲線、摩擦阻力、隔振器剛度和阻尼曲線，通過多項式的擬合獲取鋼絲繩隔振器動力方程的有關參數，為動態分析及振動響應模擬做準備。通過準靜態試驗學者們發現鋼絲繩直徑、線圈數目和位移等幾何參數對鋼絲繩隔振器垂直和水平方向準靜態載荷下滯回性能有很大的影響，能量損失比和有效剛度是評價不同鋼絲繩隔振器滯回性能的兩個重要參數[27]。Bo Cen通過對螺旋繩建立一個簡化的有限元模型[28]，采用數值模擬方法，將1+16+12單線簡化為一根單線，研究了簡化有限元模型對垂向靜剛度的影響，有限元分析得到的WRI載荷-位移關系與實驗結果的對比如圖8所示。

研究發現，不同的加載速度、預加載位移和幅值對鋼絲繩隔振器滯回性能也會產生影響。Rashidi[29]提出了一種人工神經網絡模型能夠較好的預測鋼絲繩隔振器的遲滯行為。Vaiana[30]對四種鋼絲繩隔振器分別進行小、大、較大位移的實驗，在每次靜態試驗中，水平位移以0.5 mm/s的速度線性增加，結果表明在大位移時，靜動有效剛度比趨于1。在剛度較低且位移較大的最佳荷載撓度時，剛度可以用三次硬化行為來表示。王紅霞[31]提出一種環形單元鋼絲繩隔振器，采用多個并聯的線圈作為耗能元件，研究了線圈數目、鋼絲繩直徑、繩環參數、繩環的水平傾斜角度、激勵振幅和頻率對鋼絲繩隔振器在剪切、橫滾和拉壓承載方向上遲滯特性的影響規律。鋼絲繩隔振器的幾何參數影響其力學特性，同時鋼絲繩的性能也影響著隔振器的力學性能。鋼絲繩股內應力和載荷分布對鋼絲繩性能有很大影響[32-33]。王曉宇對鋼絲繩進行參數化建模[34]，對其空間模型進行有限元分析，提出了新的鋼絲繩設計流程方法。許光鵬根據懸索的斜拋物線長度計算公式，從理論上推導撓度對鋼絲繩彈性模量影響的計算公式[35]。用縱向連續均勻假設和縱向同性假設對鋼絲繩彈性模量進行研究。

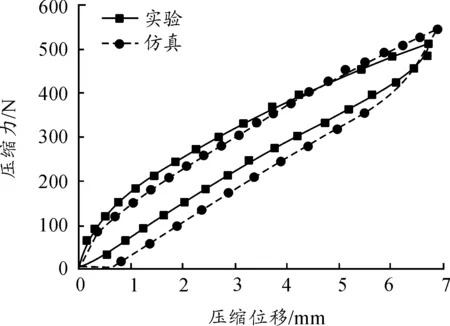
圖8 有限元分析得到的WRI載荷-位移關系與實驗結果

2)在振動試驗中，班書昊45°安裝鋼絲繩隔振器[25]，引入頻率軟化系數，結果表明有頻率軟化系數的模型比傳統的線性動力學模型更加符合實際情況。通過對鋼絲繩隔離系統施加不同幅值的掃頻正弦激勵，結果表明鋼絲繩隔振器在較寬的頻帶內(2～30)Hz，振動加速度衰減明顯，隔振效率高。朱海潮[36]將三個已成熟的HGGS-1200型鋼絲繩隔振器組成一個隔振單元，整機用10個隔振單元用于重為40t的船舶主機隔振。用功率流傳遞譜從振動能量傳遞的觀點來研究隔振問題[37-38]，功率流估算與實測的振級落差總的趨勢一致，驗證了鋼絲繩隔振器用于船舶柴油機主機隔振的可行性。其研究不同預加載和不同振幅條件下鋼絲繩隔振器的固有頻率、動剛度和阻尼時發現了不同于粘性阻尼和庫侖阻尼的對振動速度更加敏感的“高階阻尼”[39]。王江濤[40]分別研究負載質量、激勵幅值和橡膠材料對橡膠鋼絲繩復合隔振器傳遞率的影響，復合隔振器在共振時的滯回環包圍的面積大于鋼絲繩隔振器，說明了復合隔振器在共振時的隔振效率要強于鋼絲繩隔振器，橡膠鋼絲繩復合隔振器如圖9所示。

Pablo[41]在沖擊試驗的基礎上提出了一種考慮三次平穩性的杜芬振子數學模型的建立方法，同時提出一種考慮滯回特性的改進模型，在周期加載和參數識別過程中能夠進行滯回環的測量。Vaiana[30]設計了一種特殊的試驗裝置用于研究位移幅值、頻率、垂直載荷、幾何特性和鋼絲繩直徑對鋼絲繩隔振器在水平方向上即橫滾和剪切方向的動力學行為，建立的一維非線性指數模型較好的吻合試驗得到的滯回環。Buzea[42]研究表明，人工神經網絡模型能夠準確的預測鋼絲繩隔振器在各種加載條件下的行為，可用于滯回環的預測。

圖9 橡膠鋼絲繩復合隔振器

3)在沖擊試驗中，王勇[43]用錘擊法對小型鋼絲繩隔振器進行空載和有預載的沖擊特性試驗，適當加載后隔振器的抗沖擊性能可以提高，然而錘擊法并不能真實模擬沖擊信號。與錘擊法相比，氣缸式沖擊模擬臺所產生的沖擊環境與艦船設備所處的沖擊環境相比比較相似，沖擊試驗表明，鋼絲繩隔振器表現出明顯的沖擊軟化現象[44]。

Pablo[41]用不同脈沖持續時間對鋼絲繩隔振器進行沖擊試驗，在試驗的基礎上，提出一種考慮三次平穩性的Duffing振子數學模型[45-46]，使用諧波平衡法[47-49]來求解，建立了沖擊響應的數學模型。現有的沖擊考核方法主要有錘擊法跌落試驗臺和沖擊機，與前兩種方法相比，沖擊機所產生的正負雙波更能模擬真實的沖擊環境。

鋼絲繩隔振器的試驗研究主要集中在靜態和振動試驗，沖擊試驗和沖擊時的力學特性數學模型還有所欠缺。

4 結論

1)前人的研究主要集中在靜態和動態特性研究，沖擊時鋼絲繩隔振器的剛度特性、阻尼特性和遲滯力學模型的建立是值得關注和研究的重點。

2)現有的鋼絲繩隔振器動態遲滯特性力學模型描述拉壓時為對稱的遲滯特性。然而靜態和動態試驗遲滯曲線表明，鋼絲繩隔振器在拉壓方向為非對稱遲滯特性，在拉伸和壓縮時運用同倫分析方法，能夠更準確的描述其遲滯特性。

3)由于鋼絲繩隔振器非線性較強，對于其有限元實體模型的建立較困難。運用等效的方法將1+6+12鋼絲等效成單根鋼絲，建立其本構模型，從而建立準確的鋼絲繩隔振器有限元模型，運用有限元分析的方法研究幾何參數對其性能的影響。

4)對于沖擊響應的數學模型以杜芬振蕩器為原型提出具有三次彈性分量的數學模型，此模型局限于拉壓方向，沒有考慮到橫滾和剪切方向，可對沖擊響應模型進行進一步的改進。