基于空間Agent的艦載機群調度路徑規劃
張鵬翼,黃百喬,崔博文
(1.中國船舶工業系統工程研究院,北京 100036;2.北京航空航天大學可靠性與系統工程學院,北京 100191)
艦載機的調度能力是艦載機出動與回收能力的重要基礎,但調度方案受到有限艦面空間的嚴重制約,但調度方案受到有限艦面空間的嚴重制約,必須進行合理調度路徑規劃,以減少艦載機群調度時間,提高機群調度效率[1-6]。
目前應用較為廣泛的算法包括A*搜索算法[7-9]、引力搜索算法[10]、Dijkstra算法[11]、模擬退火算法[12]、遺傳算法[13]、粒子群優化算法[14-15]、Multi-agent協同路徑規劃[16],以及隨機生成樹等方法[17]。
一些研究將艦載機視為質點,未考慮調度路徑的干涉問題,這導致路徑可執行性下降。常見的解決方案是按圓形、多邊形等幾何形狀對實體和障礙物進行抽象,通過檢測距離實現碰撞檢測[18]。
Multi-Agent在群體路徑規劃方面已有很好的應用,且Agent技術可支持對Agent外形尺寸的描述。為此,本文擬基于Multi-agent技術,考慮空間約束以及避障等需求,通過改進的A*算法研究艦載機群多機協同路徑的聯合規劃問題[4,19-20]。
1 機群路徑規劃過程
艦載機群的調度過程是艦載機在各個機務站位從規定位置或給定位置到達指定機務站位的過程。以起飛調度過程為例,其基本情況如圖1所示。
本文考慮一個包含N架次艦載機的機群編隊,可用起飛站位的數量為M(M (1) 多機多點的調度環境下,調度過程需滿足一些約束條件,包括飛機調運最大速度v、飛機起飛位上的最長占用時間為TD、飛機調度中飛機的偏轉角的最大值Ψ。 同時,在機群調度的過程中,應避免干涉,包括兩類:即飛機與固定障礙物的靜態干涉、兩架飛機同時移動時發生的動態干涉。為此給出飛機的最小安全距離d。 2.1.1空間柵格模型 柵格法[21-22]是路徑規劃中常用的環境建模方法,本文借助柵格法對航母艦面環境進行建模。由于正六邊形柵格具有步間轉角適當、障礙物覆蓋能力強等優點[23],本文采用正六邊形柵格對空間環境進行分割,空間柵格模型如圖2所示。柵格數量為m×n個,每個柵格的編號分別用二維坐標(i,j)來表示,其中i表示行坐標、j表示列坐標。每個柵格可按兩種狀態進行初始化,0表示該柵格被占用、1表示該柵格未被占用。劃分的柵格覆蓋所有有效的艦面空間范圍。 在此基礎上,給出一種考慮安全碰撞距離的柵格尺寸的界定方式。調度過程中,飛機作為不規則形狀,可以簡化為一個包絡圓形,設半徑為R。已知飛機的安全碰撞距離為d,飛機的中心位置為Oi,則飛機與障礙物的距離應滿足d(O1O2)>2R+d。柵格劃分規則為:(1)以O1,O2為圓心,以(R+d/2)為半徑對兩圓進行擴展,形成兩個相切圓;(2)分別作兩個圓的外接六邊形,單個柵格形狀為相切圓的外接六邊形。則可以計算出邊長為: (2) 2.1.2空間Agent的基本屬性描述 將每個離散的柵格抽象為空間Agent,并對空間Agent的基本屬性進行如下描述。 1)空間Agent的位置 L={I/I=[x,y]T, 0≤x≤X, 0≤y≤Y} (3) 式(3)中:X,Y分別表示整個空間行坐標與列坐標的最大值。空間Agent依據位置設定優先級,假設跑道位置上的優先級低。 2)空間Agent的狀態集 設置C={-1,0,1}三種狀態,-1表示固定占用空間,該空間的狀態為一直不可用;0表示臨時占用,并假設該空間在有限的時間t后可變為可用狀態;1表示該空間可用。 3)空間Agent的鄰居 每個柵格都至少與一個其他柵格相連接,定義空間Agent鄰居,Lk(xk,yk)表示某一空間Agent的位置,Lk+1(xk+i,yk+i)表示該空間Agent的鄰居坐標,則該空間Agent的鄰居集合為: (4) 在整個機群的路徑規劃中,飛機所經過的空間Agent連接關系構成了飛機Agent移動的路徑。 定義飛機Agent集Ω,且每個飛機Agent在任意空間中的狀態為: p=〈A,θ,v〉 (5) 式(5)中:A表示飛機的位置,A應滿足與某個空間Agent的位置重合;θ表示為當前位置距離目標位置偏角;v為考慮方向的飛機移動速度,其方向為η。 定義飛機Agent在某一k柵格時的狀態為pk={Ak,θk,vk}∈P,其中P為np維度的狀態空間;飛機Agent選擇空間Agent的控制函數為wk=g(v,ψ,d,ω),wk體現了根據飛機Agent轉移時的速度、偏轉角、安全距離及目的角度等參數作為飛機Agent決策指標。飛機動態路徑規劃問題可以描述為以下狀態方程,即: (6) 飛機Agent運動行為學狀態圖見圖3。飛機調度至目標位置的行為可用飛機Agent距離目標位置的偏離函數fgoal表示,fgoal越大越不利于靠近目標位置,fgoal可表示為: fgoal(Ai)=α1θ(Ai)+α2φ(Ai) (7) 式(7)中:θ(Ai)表示飛機Agent在位置Ai時距離目標位置G的角度;φ(Ai)表示該飛機Agent在位置Ai時的運動方向與飛機目的位置方向的偏差,且φ(Ai)=η(Ai)-ω;α1,α2表示飛機Agent的兩個偏移角度要素對其奔向目標的作用權重,且α1+α2=1。 圖3 飛機Agent運動行為學狀態圖 飛機在路徑規劃中存在的3種干涉情況: 飛機Agent在對下一個空間Agent進行搜索時,可實現障礙探測距離不小于(2R+d),這樣可以保證飛機提前轉變移動方向,避免與障礙物相撞。 定義如下的機群單架飛機路徑規劃的代價函數f為: f(Ai)=g(Ai)+fgoal(Ai) (8) 式(8)中:g(Ai)是飛機Agent移動到Ai位置實際花費時間;fgoal(Ai)是飛機Agent距離目標位置偏離函數,可以將其作為飛機Agent搜索下一個空間Agent的啟發式函數。 飛機Agent與空間Agent的交互規則如下: 規則1:空間Agent選擇規則。 1)飛機Agent在接到任務后,需要從其當前所屬空間Agent的鄰居集合Neighbor(Ai)中選擇下一個路徑點,Ai表示飛機Agent當前位置;在控制函數wk=g(v,ψ,d,ω)的約束下,應滿足: (9) θ(Ai)>90°時,表示飛機在目標位置的前方,因此應設定α1占較大比重,且移動后方向為φ(Ai+1)=min{θ(Ai),φ(Ai)+Ψ},從而保證飛機Agent從正向移動至目標位置,提高規劃的成功率。 θ(Ai)≤90°,φ(Ai)≥90°時,表示飛機在向遠離目標位置的方向移動,因此,應設定α2占大比重,且移動后的方向為φ(Ai+1)=min{θ(Ai),φ(Ai)-Ψ}從而使得飛機能夠改變移動方向,向目標位置移動。 θ(Ai)≤90°,φ(Ai)≤90°時,表明飛機Agent正在向目標位置移動,可設置α1,α2均衡比重,且移動后的方向為φ(Ai+1)=min{θ(Ai),φ(Ai)-Ψ},保障飛機平穩向目標移動。 在飛機Agent的單次規劃距離2R+d內,飛機可以到達所有Selected(Ai)中的位置。假設飛機Agent從當前位置到Selected(Ai)中每個空間Agent所經歷的時間T(φ,θ)是φ,θ的函數,可表示為: (10) 由于它對飛機Agent移動時間產生影響,fgoal是影響飛機Agent選擇空間Agent的另一要素,因此,定義: ming(Ai+1)+fgoal(Ai+1) (11) 式(11)是飛機Agent選擇下一個空間Agent的依據,其中g(Ai+1)=g(Ai)+T(φ,θ),fgoal(Ai+1)是飛機Agent在Selected(Ai)中每個空間Agent上距離目標位置G的偏差函數。 代價函數的值相等時,應遵循先入為主的優先原則以及空間Agent的優先級順序。 規則2:空間Agent沖突解決規則。 基于兩類Agent的飛機路徑規劃規則,給出機群基于A*算法的啟發式路徑規劃算法的執行過程如圖4所示。 圖4 機群路徑搜索算法執行過程 本方法將Agent之間的協商過程融入到路徑A*算法的實現過程中,可有效地解決機群多機同時調度的碰撞問題。 假設航母艦面的飛行甲板為斜直兩段式甲板,尺寸約為330 m×80 m,艦載機的尺寸為20 m×15 m(展翼狀態),如圖1所示。以艦載機作戰的典型任務模式連續出擊為例。假設機群某波次任務需出動10架次飛機,這些飛機需要從初始停放位置調度到彈射起飛的準備位,并要求機群調度過程為并行作業。 每個飛機初始位置、飛機朝向、目標位置等相關參數如表1所示,表1中包含了每架飛機的調度開始時間和目標位置信息。設飛機調度過程最大轉角度為60°,最高速度為1.5 m/s,最小安全距離為2 m,飛機起飛位上的準備時間為服從N-(1.8,0.52)的正態分布,定義起飛任務開始的時刻為0時刻。 表1 機群飛機相關參數 以A3和A4飛機調度過程對機群路徑規劃進行說明,其中的避碰實現過程如圖5所示。在第191 s時,A3調用空間Agent選擇模塊,并根據算法選擇了位置(745,171)的空間Agent,并發現該點已經被A4飛機臨時占用,因此A3選擇了等待策略,直到A4釋放了該點之后,才完成了移動。飛機A3和飛機A4的路徑節點分別為: A3:(690,76)-(745,171)-(800,226)-(910,226)- (1 020,226)-(1 130,226)-(1 240,226); A4:(415,171)-(525,171)-(635,171)- (855,171)-(965,171)-(1 075,171)- (1 185,171) 圖5 機群動態避障的過程 全部機群路徑規劃結果如表2所示。 表2 機群路徑規劃結果 在本次仿真中,從第一架飛機開始到最后一架飛機完成起飛所花費的總時間為658 s,這一結果說明本文所構建的模型是合理可行的。 1)在機群路徑規劃的研究中,要考慮艦載機的空間特征對機群調度的影響。 2)利用正六邊形對機群調運的空間環境進行柵格建模,并確定空間環境Agent和飛機Agent。 3)考慮機群調度中的碰撞問題,引入等待策略和繞行策略對機群路徑規劃的影響,并利用改進A*算法對飛機Agent 的調度路徑進行規劃,實現了機群調度的全局最優。 本文中的研究仍需要進一步深化,例如可以對艦面環境進行更精確的建模,從而實現路徑規劃的更優性研究。2 基于Multi-Agent的艦載機調度問題建模
2.1 空間環境Agent
2.2 飛機Agent



3 基于改進A*算法的艦載機Agent協同路徑搜索算法
3.1 代價函數

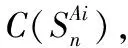


3.2 算法的執行過程

4 仿真案例



5 結論

