柔性并聯機構殘余振動控制

張清華

(佛山科學技術學院 機電工程學院，廣東 佛山 528231)

剛柔耦合柔性并聯機構的彈性動力學建模及振動主動控制一直是機構學研究熱點[1-3]。由于其動態性能好、操作靈巧、能耗低，可以實現高速、高加速度運動，廣泛應用在高端電子芯片制造、精密加工、細胞操作等領域。最近幾十年來，通過眾多學者持續不斷的努力，動力學建模理論已取得了許多有意義的成果[4-6]。然而，高速、高加速度柔性并聯機構由于其剛度較小，容易產生彈性振動，其殘余振動嚴重影響其重復定位精度，因此，必須對其彈性振動進行有效的控制。目前，柔性機構的振動控制方式主要有被動(如添加阻尼材料、增大系統剛度)和主動兩種[7]，其中基于壓電陶瓷傳感器和致動器的主動控制方式是近年來研究熱點[7-9]，但控制對象主要集中在柔性轂-梁機構、兩連桿柔性機構、多連桿簡單柔性機構(如四桿機構、鏈等)[10-12]。對復雜的柔性并聯機構，相關研究成果較少[8,13-16]，控制方法主要集中在應變速率反饋控制、應變與應變速率反饋控制、最優狀態反饋控制等。但這些控制沒有考慮模態截斷引起的觀測和控制“溢出”問題，魯棒性較差，而滑模變結構控制具有良好的抗外部干擾和參數擾動性能，魯棒性好，因此，本研究將對一類高速柔性并聯機構進行研究，著重探討滑模變結構控制在柔性并聯機構殘余振動主動控制方面的可行性和優越性，提高其重復定位精度，為高速精密定位平臺提供理論基礎。

1 柔性并聯機構彈性振動控制方程

為了建立該柔性并聯機構的動力學控制方程，采有限元法對柔性連桿進行梁單元劃分，考慮壓電陶瓷傳感器和致動器的正逆壓電效應，基于拉格朗日方程建立了智能梁單元的彈性動力學方程，假設整個系統有個致動器和個傳感器，考慮單元間的約束關系可建立系統總的彈性動力學方程[4,16]，

(1)

本研究的目標是抑制柔性構件的殘余振動，以使動平臺快速、精確地穩定在目標位置。殘余振動是機構在名義運動結束后由于負載和自身的慣性和伺服電機的耦合作用而引起的柔性構件的振動。因此，式(1)的系數矩陣中與名義運動速度和加速度相關的量都為零。從而, 質量矩陣M為對稱正定常數矩陣，剛度矩陣K為對稱定常矩陣，外力矩陣Q為零矩陣。根據模態理論，系統的彈性振動主要由其低階模態決定。采用實模態方法，把物理空間描述的動力學方程變換到模態空間上，并取其前r階低階模態進行控制。因此，系統的控制模型可以簡化為：

(2)

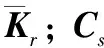
把式(2)寫成狀態空間的形式，得

(3)

2 滑模變結構控制器設計

設狀態變量為Xc(t)，理想的狀態Xcd(t)=0，因此系統跟蹤誤差及其導數為：

(4)

則切換函數矩陣s(x)可表示為：

s(t)=He(t)

(5)

其中H為m×2r階矩陣。

本研究采用指數趨近律迫使系統從任意初始狀態趨向切換面，直到到達切換面，即

(6)

s(t)T(-diag(εi)sgns(t)-diag(ki)s(t))≤

(7)

解不等式(7)，可得[17]：

(8)

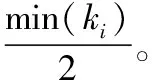
根據式(3)和指數趨近律式(6)，可求得控制函數：

Vin=(HBc)+(-diag(εi)sgns(t)-diag(ki)s(t)-HAcXc)

(9)

3 仿真與實驗

如圖1所示，以一平面完全對稱的3-RRR柔性并聯機構為例，對上述滑模變結構控制器進行數值仿真分析，驗證該控制器可以有效地抑制柔性連桿的殘余彈性振動。

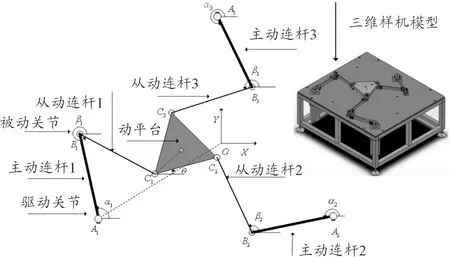
圖1 平面3-RRR柔性并聯機構示意圖

假設動平臺中心點的運動軌跡為：

(10)

主動連桿、被動連桿及動平臺的材料都是鋁合金,主動連桿是剛性的，被動連桿是柔性的。假設連桿兩端的集中質量為0.2 kg，集中轉動慣量為0.000 5 kg·m2.每根柔性桿被劃分為3個單元，2對PZT致動器對稱地粘貼在每根被動柔性桿的第一、三單元的中間位置,PZT傳感器粘貼在第二單元中間位置，桿件參數和PZT致動器和傳感器參數見表1。取系統前三階模態作為被控模態[12]，取矩陣H=[2*II]，diag(εi)=0.000 03*I,diag(ki)=15*I，I為3×3的單位矩陣。

表1 構件參數

首先，動平臺按照式(10)給定的軌跡做圓周運動，運動一個周期后名義運動停止，開始施加控制。圖2是3根主動連桿與相應的被動柔性連桿在X方向的最大彈性位移隨時間的變化情況；圖3是3根主動連桿與相應的被動柔性連桿在Y方向的最大彈性位移隨時間的變化情況,從圖3、圖4可知，被動柔性連桿的最大彈性位移比相應的主動連桿大，這符合本文的主動連桿是剛性的假設。圖4、圖5、圖6分別是在沒有控制和滑模變結構控制下動平臺在X方向、Y方向的彈性位移以及彈性轉角隨時間的變化情況；從圖4、圖5、圖6可知，柔性連桿和動平臺的彈性振動呈衰減振蕩趨勢。

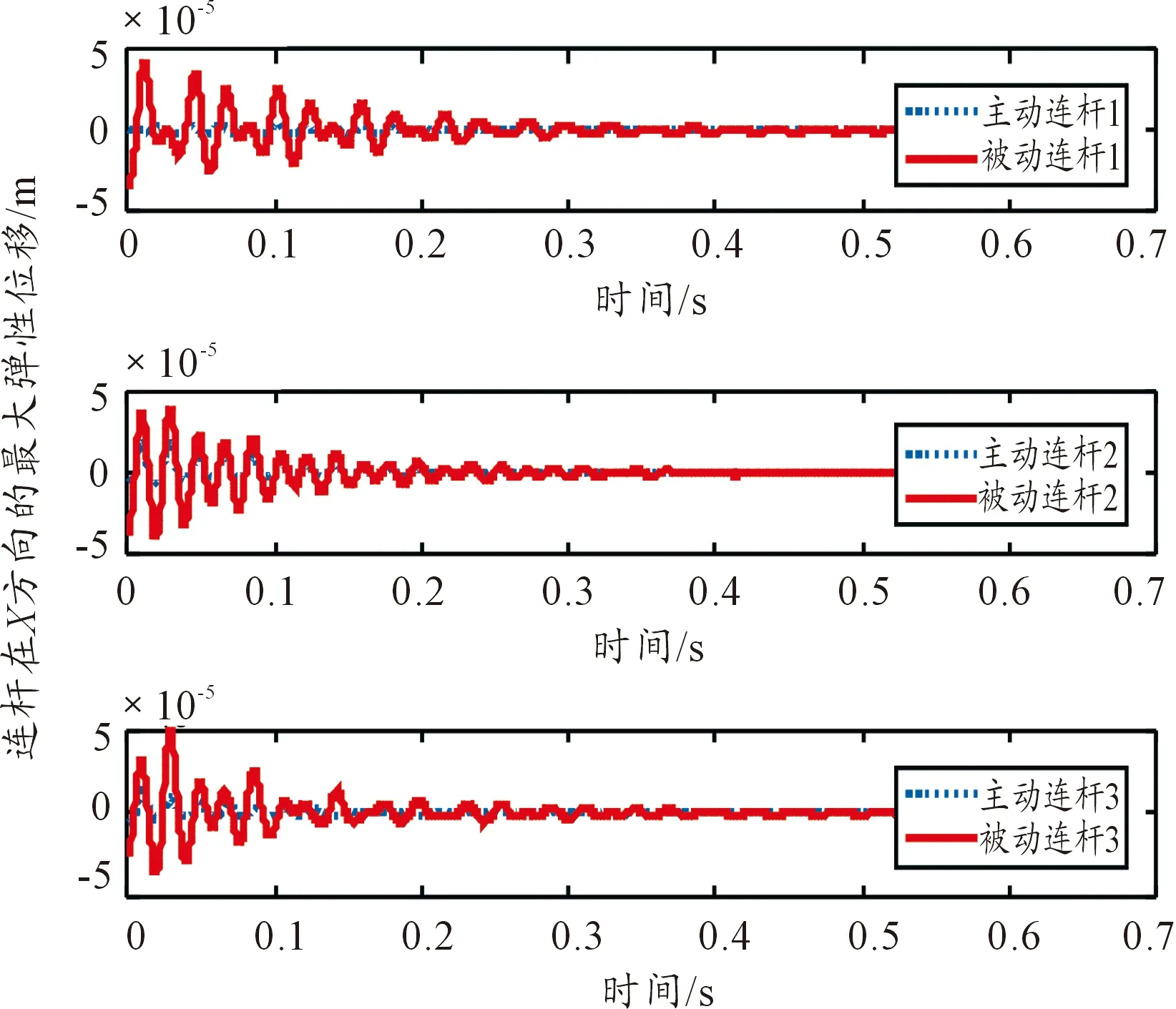
圖2 所有主動連桿與相應的被動連桿在X方向的最大彈性位移隨時間的變化情況

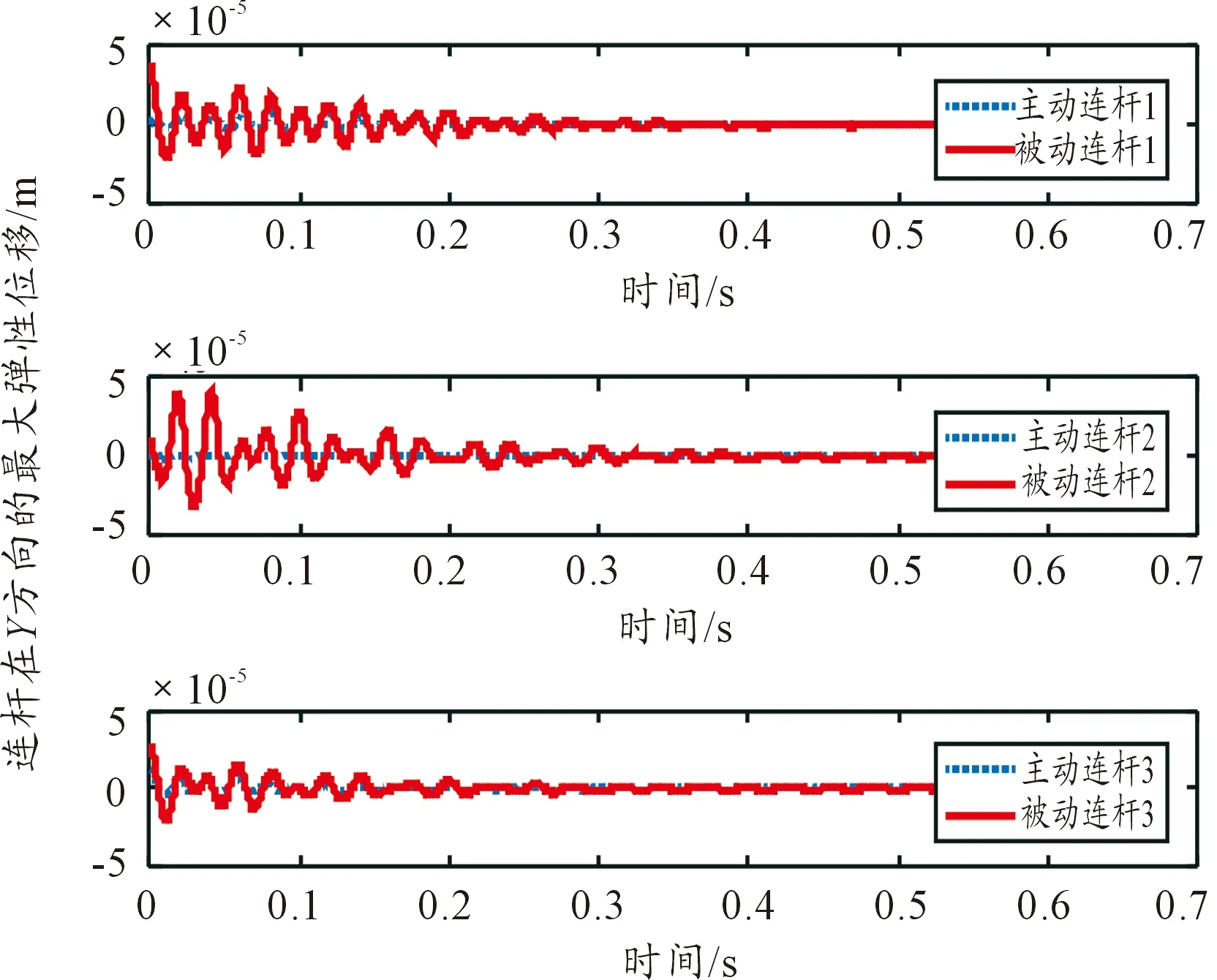
圖3 所有主動連桿與相應的被動連桿在Y方向的最大彈性位移隨時間的變化情況

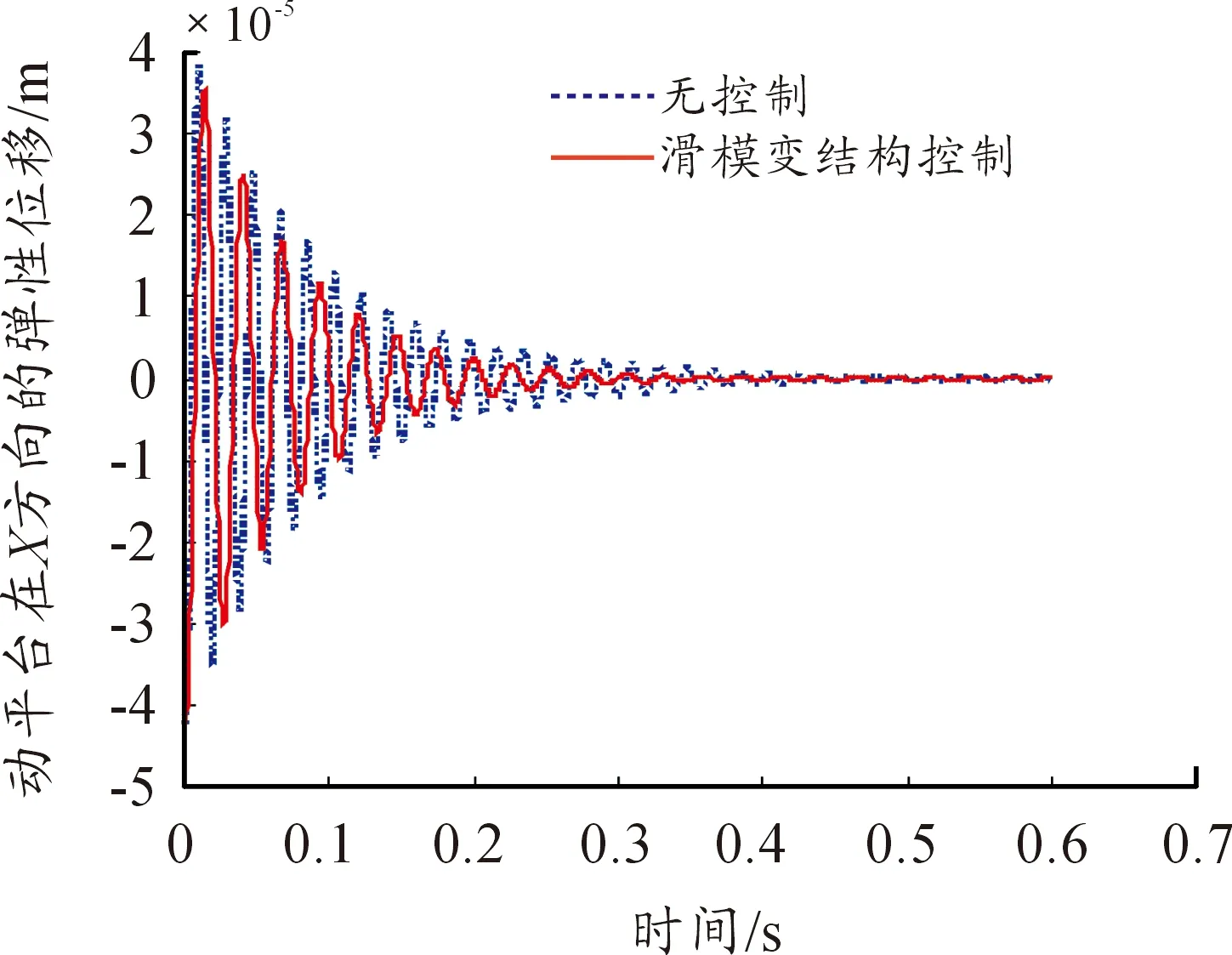
圖4 在沒有控制和滑模變結構控制下動平臺在X方向的彈性位移隨時間的變化情況

圖5 在沒有控制和滑模變結構控制下動平臺在Y方向的彈性位移隨時間的變化情況

圖6 在沒有控制和滑模變結構控制下動平臺的彈性轉角隨時間的變化情況

在滑模變結構控制下，振動迅速趨于0，且沒有“抖振”現象發生，因此，基于指數趨近律的滑模變結構控制可以有效地抑制動平臺的殘余彈性振動，進而提高動平臺的重復定位精度。

圖7、圖8、圖9分別是施加在三根柔性梁致動器片上的控制電壓，通過PZT致動器正壓電效應。抑制柔性連桿的彈性振動，進而抑制動平臺的彈性振動。從圖7、圖8、圖9可知，最大控制電壓在被動柔性連桿1的PZT致動器對上，大小為270.5 V，大部分時間的控制電壓限制在以內。被動柔性連桿3上的PZT致動器對所需的電壓信號最小，同時，控制電壓隨著柔性連桿彈性振動的減小而減小。

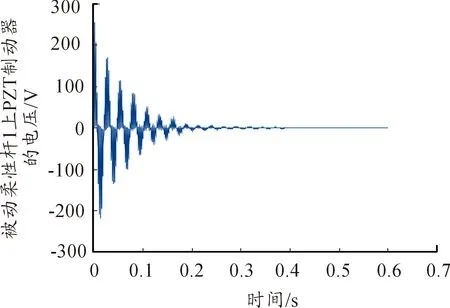
圖7 被動柔性連桿1上PZT致動器上所施加到電壓隨時間的變化情況

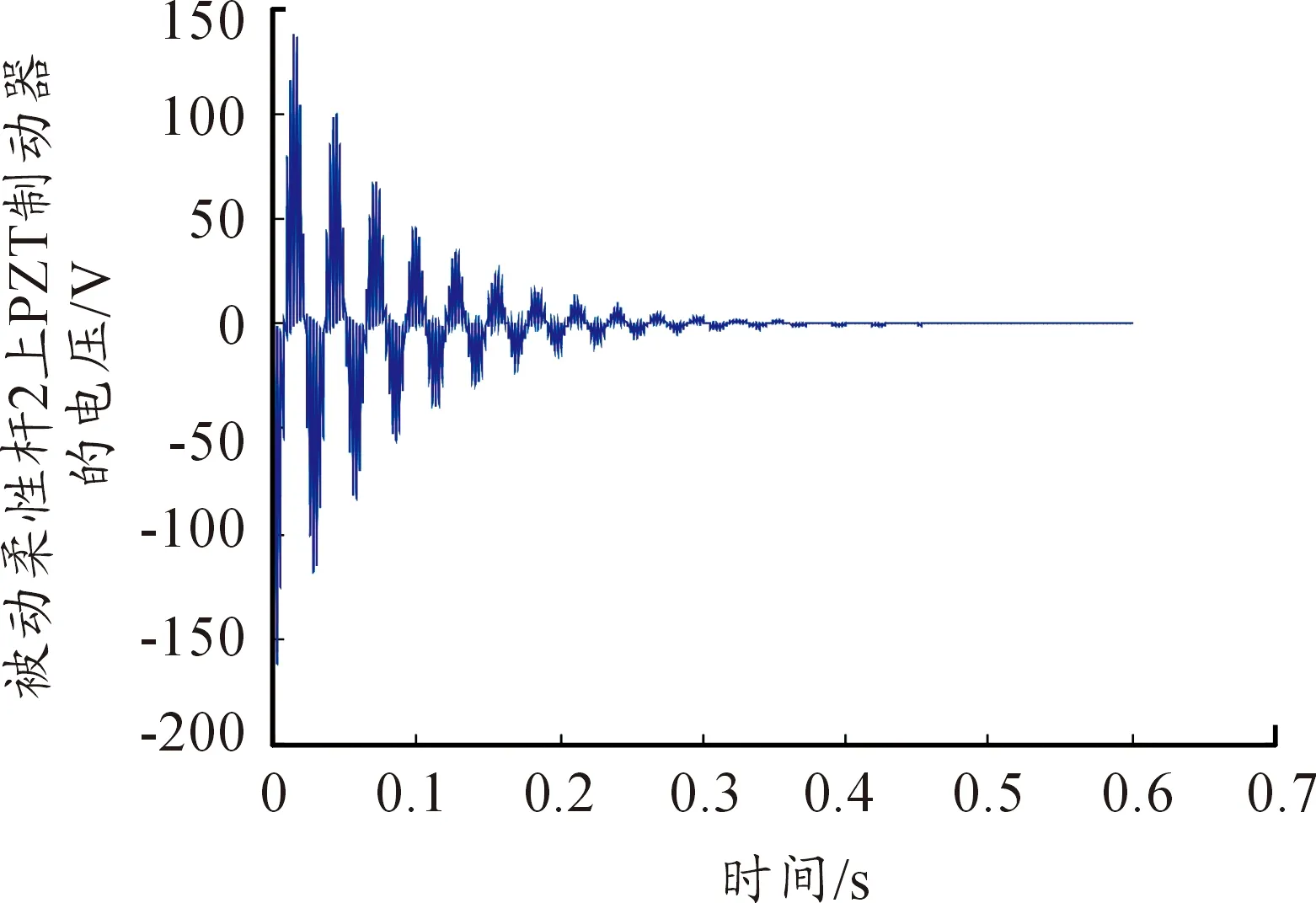
圖8 被動柔性連桿2上PZT致動器所施加到電壓隨時間的變化情況

圖9 被動柔性連桿3上PZT致動器所施加到電壓隨時間的變化情況

為驗證滑模變結構控制算法的有效性，搭建了一套實驗系統，實驗系統如圖10所示，主要由平面3-RRR柔性并聯機構、壓電陶瓷傳感器和致動器、電荷放大器、壓電陶瓷驅動電源、半物理仿真控制系統dSPACE-DS1103等組成。其中3根被動連桿為柔性，尺寸參數為：252 mm×25 mm×3 mm；主動連桿為剛性，尺寸參數為：254 mm×25 mm×10 mm，主、被動桿、動平臺以及旋轉關節材料均為鋁合金，為使桿件表面絕緣，對其進行氧化處理。為方便電機的安裝和良好的隔振，靜平臺由大理石、鋼架結構和長方形鋼板組成。壓電陶瓷片有兩種規格，一種尺寸為：50 mm×25 mm×2 mm，用作致動器；另一種尺寸為：30 mm×15 mm×1 mm，用作傳感器。由保定宏聲科技有限公司提供。

圖10 實驗系統

振動控制實驗過程如圖11所示，PZT傳感器測量柔性連桿的彈性振動位移信號，經電荷放大器放大后傳遞給dSPACE控制器，通過上位機控制算法計算出所需的控制量，再通過dSPACE的DAC口傳遞給壓電陶瓷驅動電源，放大的電壓信號再施加給PZT致動器對，進而抑制柔性連桿的彈性振動，最終實現動平臺的快速鎮定。

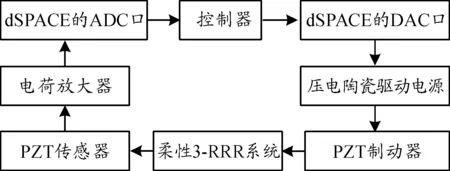
圖11 振動控制過程框圖

實驗過程如下：動平臺按給定軌跡運動一個周期[16]然后停止。PZT傳感器片采集的振動信號反饋給同一桿上的兩對PZT致動器。因此整個系統有3個PZT傳感器，6對PZT致動器。取動平臺名義運動停止后2.7 s內的數據進行分析，在Matlab/Simulation中設置采樣頻率為0.1 ms，即從每路傳感器各提取了2.7萬個數據。圖12至圖14分別是3片PZT傳感器在控制和未控制時測得的柔性連桿1、2、3的振動信號曲線。從傳感器測得的振動信號可知：本文設計的滑模變結構控制器可有效地抑制柔性連桿的殘余彈性振動。

圖12 傳感器1測得的振動信號

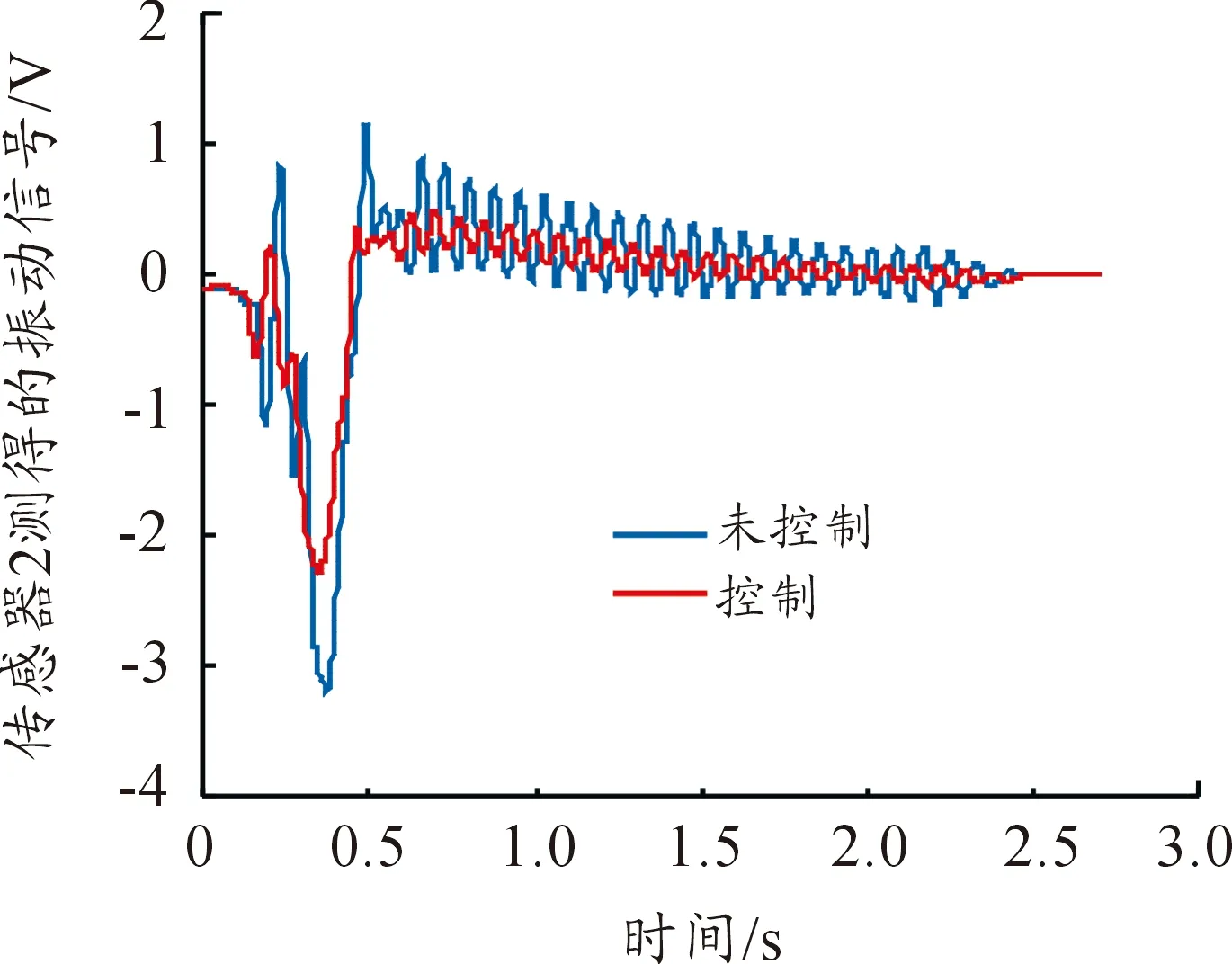
圖13 傳感器2測得的振動信號

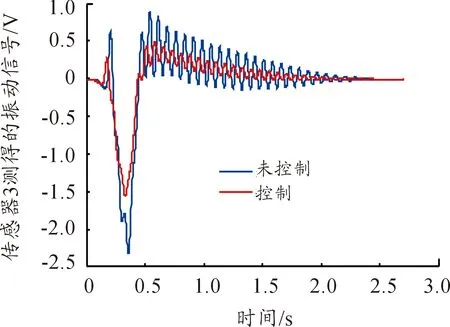
圖14 傳感器3測得的振動信號

圖15是柔性連桿3在未控制、應變率反饋控制[16]、滑模變結構控制三種情況下的第一階模態(第一階固有頻率是12.5 Hz)的功率密度譜，在應變率反饋控制下第一階模態功率密度譜下降了42.30%，在滑模變結構控制下第一階模態功率密度譜下降了68.90%，對比應變率反饋控制，滑模變結構控制能獲得了更好的控制效果，具體數據見表2所示。

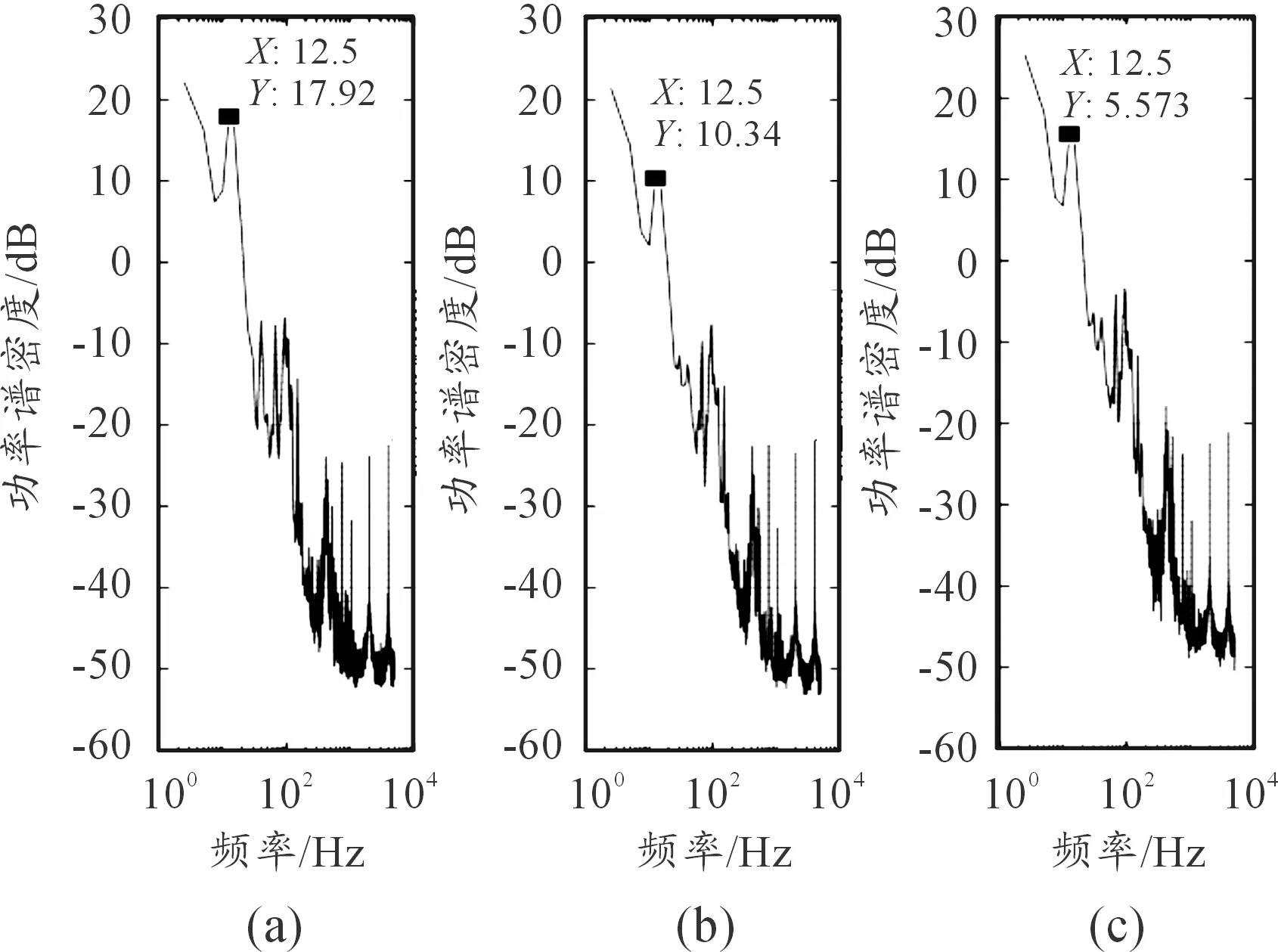
圖15 功率密度譜

表2 三種情況下柔性連桿3的第一階固頻的功率密度譜 dB

4 結論

本研究基于已建立的柔性并聯機器人機構的彈性動力學方程，采用模態截斷理論，把高維彈性動力學方程化為r階解耦方程。基于Lyapunov穩定性理論，采用指數趨近律函數，設計了多維滑模變結構控制器。驗證了該控制器能有效地抑制并聯機器人機構柔性連桿的彈性振動，進而可提高系統動平臺的定位精度，通過與應變率反饋控制方法進行比較，得出滑模變結構控制在較低的控制電壓下能取得更好的控制效果，其第一階模態的功率密度譜下降68.90%，好于已有的控制結果[15-16]。