某鏈式自動炮分度機構剛柔耦合動力學特性研究

王 凱，李 勇，田 楠，申亞琳

(西北機電工程研究所，陜西 咸陽 712099)

鏈式自動炮是一種通過鏈條周向轉動驅動炮閂往復運動來完成解鎖、開閂、抽筒、供彈、輸彈、關閂、閉鎖、擊發等動作的外能源自動炮[1]。分度機構作為鏈式自動炮的關鍵分度機構，負責協調鏈式自動炮進彈輪與各傳動系統間的運動關系，對鏈式自動炮運動的準確性和協調性起著重要作用[2]。

目前，分度機構的相關研究主要集中在兩個方面：一方面，通過對分度機構的分度輪輪廓曲線、中心距、分度滾子數等進行參數化理論設計，得到較優的傳動效果[3-4]。另一方面，考慮機構變形對分度機構的動力學特性影響，通過建立與實際工況環境相符的剛柔耦合動力學模型和動力學虛擬樣機，模擬不同因素對其動態性能的影響。分度機構參數化理論設計已趨于成熟，鮮有創新改進。分度機構的現有剛柔耦合動力學研究，大多以ANAYS、Pro/E、ADAMS三種平臺，基于模態縮減法建立分度機構的剛柔耦合動力學模型，進行不同因素對其扭轉振動和最大加速度影響[5-6]。基于模態縮減法建立的剛柔耦合動力學模型，存在無法直接建立模態柔性體與其他構件的接觸、模型修改困難繁雜、只能描述小變形的線性變形等缺點。有限元柔性體技術則可有效地避免上述問題[7]。另外，鏈式自動炮分度機構傳動具有高速、瞬時強沖擊等特點，其傳動過程中的碰撞力極大影響整體系統的可靠性、構件疲勞壽命等。顯然，上述分度機構的剛柔耦合動力學研究未對傳動過程中的沖擊碰撞特性進行相關研究。

因此，本研究以分度機構中的輸出軸作為柔性體，其余構件作為剛性體，采用有限元柔性體建模原理，基于UG三維軟件和Recurdyn多體動力學分析軟件建立分度機構的剛柔耦合動力學模型，研究不同因素(粘性阻尼系數、分度輪輸入轉速、嚙合間隙)對傳動過程中的碰撞力影響，為分度機構的設計與優化提供依據。

1 鏈式自動炮分度機構

鏈式自動炮示意圖如圖1，其工作原理如下：電機動力經過一對換向齒輪傳動分為兩路，第一路通過鏈條往復運動驅動閂體完成進彈、閉鎖、擊發、抽殼等動作；第二路經分度機構驅動進彈輪轉動，完成撥彈動作。兩路運動通過分度機構協調各傳動系統間的運動關系，實現供彈與輸彈動作的交接過程。

分度機構是一種將輸入軸的連續轉動轉化為輸出軸間歇轉動的傳動機構。在鏈式自動炮中，其間歇運動頻率與鏈式自動炮的射速匹配一致，屬于高速高精度運動，具有瞬時強沖擊碰撞特點。高速運動加劇傳動過程中的沖擊碰撞，影響系統整體傳動的穩定性。同時，強沖擊碰撞使得分度機構的嚙合情況惡化，加速磨損運動構件，產生嚙合間隙，進一步惡化傳動工況環境情況。

圖1 鏈式自動炮示意圖

2 分度機構剛柔耦合多體動力學建模

2.1 有限元柔性體理論

有限元柔性體MFBD(Multi-Flexible-Body Dynamics)首次實現了有限元技術與多體動力學的有機結合，克服了模態柔性體的缺點，采用節點之間的相對位移和旋轉作為節點坐標來描述結構的變形，具有較高的計算精度[8-9].理論數學建模原理如下：

在空間梁單元結構中，取任意兩單元i-1和i，如圖2所示。坐標系X-Y-Z為總體慣性坐標系；xk-yk-zk為節點k的節點坐標參考系；rk表示節點k在總體慣性坐標系的位置矢量；x(i-1)i-y(i-1)i-z(i-1)i為固結在節點i上，關于節點i-1的隨體坐標系。

圖2 梁單元變形示意圖

節點i在慣性坐標系X-Y-Z中的位置矢量分別用節點i-1的位置矢量，以及與節點i-1相對變形表示為

(1)

相對角速度wi與wi-1的關系可表示為：

(2)

通過對式(1)、式(2)利用虛位移原理進行變化并聯立，可得相鄰節點虛位移關系。反復遞推就可以得到整個系統節點之間的相對虛位移關系

δZ=Bδq

(3)

同理，對式(1)、式(2)求導，聯立得到系統在慣性坐標系下的節點速度與相對速度的關系；節點的加速度可通過上述速度關系求導獲得。

系統運動在慣性坐標系下的Euler-Lagrange基本方程，如下：

(4)

式中，Φ為約束矩陣；λ為拉格朗日乘子。

將式(3)代入到式(4)中，得到

(5)

由于δq是任意的，從而得到系統的動力學方程為：

(6)

2.2 建立幾何模型

分度機構采用雙層共軛滾柱凸輪驅動，用于兩軸間的傳動，主要由分度輪、輸出軸、滾子、滾子帽組成，如圖3所示。分度輪由前片凸輪和后片凸輪組成，前、后片凸輪的輪廓曲線一致，呈一定角度錯開。滾子呈兩層均勻安裝在輸出軸上，與前、后片凸輪嚙合。

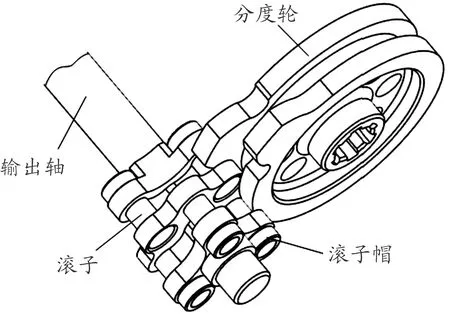
圖3 分度機構組成示意圖

幾何模型建立過程如下：基于分度輪外輪廓曲線、壓力角、中心距等，利用Matlab軟件編程得到分度輪外輪廓數據；基于分度輪輪廓數據云，利用三維建模軟件UG繪制某鏈式自動炮分度輪并與其他構件裝配；將UG裝配模型導入到多體動力學仿真軟件Recurdyn中，設置材料屬性:彈性模量2.06×1011Pa、剪切模量7.782×1010Pa、密度7.85×103kg/m3。本研究采用的分度輪外輪廓曲線如式(7)所示，式中，θ分度輪角位移；φ為輸出角位移；θf=52°；h=2.6；θ1=5.846 2°；θ2=46.153 8°。

(7)

2.3 施加約束和接觸

根據分度機構構件的連接和運動關系，在Recurdyn軟件中建立約束和接觸如表1所示。其中，分度輪與滾柱之間的Extend Surface to Surface Contact面接觸計算是一個不斷檢測的過程，根據穿透深度及變化來計算接觸力。當計算過程中分度輪與滾子的實際穿透深度小于最大穿透深度時，計算接觸力；一旦檢測到實際穿透深度大于最大穿透深度，則接觸失效，不再計算接觸力[7-8]。本文根據工程經驗設置最大穿透深度0.1 mm。接觸理論采用非線性彈簧阻尼模型，其法向接觸力計算公式：

(8)

(9)

(10)

式中：k為接觸剛度系數；c為粘性阻尼系數；δ為接觸穿透深度；m1為剛度指數；m2為阻尼指數；m3為凹痕指數；μ1、μ2為接觸物體材料的泊松比；E1、E2為接觸物體材料的彈性模量。

表1 分度機構約束和接觸

2.4 剛柔耦合多體動力學模型

鏈式自動炮分度機構輸出軸的動力學特性體現分度運動的準確性。綜合考慮仿真精度、計算速度等因素，本文對分度機構中的輸出軸利用Recurdyn軟件中的mesh工具進行了有限元柔性化處理，其余構件依舊作為剛性體。輸出軸經過有限元處理后，在滾子繞輸出軸旋轉運動副以及輸出軸旋轉運動副處自動生成了剛性單元(FDR單元)，方便運動和接觸關系的建立。分度機構的剛柔耦合多體動力學模型如圖4所示。

3 不同因素剛柔耦合動力學響應分析

經過多次工程實踐經驗發現，分度輪輸入轉速、嚙合間隙、粘性阻尼系數對鏈式自動炮分度機構運動特性起主要影響作用。因此，本文以此三因素為變量，研究傳動過程中的碰撞力變化規律，為分度機構的設計與優化提供依據。

1)粘性阻尼系數

分度輪與滾子接觸模型利用非線性阻尼模型來計算粘性阻尼系數，該模型認為物體表面接觸-碰撞過程中的能量是由粘性阻尼引起的。該阻尼與剛度系數、接觸穿透深度、碰撞速度、彈性恢復系數有關，上述參數又與接觸物體的材料、碰撞表面曲率、潤滑脂的粘度等有關，很難進行精確計算。根據工程經驗，粘性阻尼系數一般取剛度系數的0.1%～1%[10]。剛度系數利用式(9)、式(10)代入分度輪和滾子的相應的材料參數為5.81×105N/mm。因此，本文結合仿真情況取0～800 N·S/mm作為粘性阻尼系數的參數范圍。

2)分度輪輸入轉速

分度機構中分度輪輸入轉速與鏈式自動炮射頻相匹配，高射頻加劇了分度過程中沖擊碰撞情況，影響供輸彈系統運動的準確性和可靠性。因此，本文結合鏈式炮實際射頻情況取200～600發/min作為分度輪輸入轉速的參數范圍。

3)嚙合間隙

安裝誤差和加工誤差產生的間隙直接影響分度盤與滾子的嚙合情況，從而影響傳動的平穩性和準確性。另外，隨著嚙合磨損的累積，滾子和分度輪之間的嚙合間隙會變得越來越大，且無法避免。因此，本文結合實際工程情況取0.1～1 mm作為嚙合間隙的參數范圍。

3.1 粘性阻尼系數影響

為研究接觸阻尼系數對于分度機構動力學特性的影響，在分度輪輸入轉速300 r/min、嚙合間隙0.1 mm時，粘性阻尼系數分別取0、100、…、700、800 N·S/mm。從圖5得出，隨著粘性阻尼系數的增大，碰撞力曲線規律不再平穩，尖點毛刺增多。提取出不同粘性阻尼系數的最大碰撞力特征值如表2所示，并繪制出圖6所示的曲線，可知：碰撞力最大值隨粘性阻尼系數增大整體呈先緩慢、后急劇遞增趨勢。在0～200 N·S/mm區間增大時，碰撞力最大值呈現近似線性緩慢遞增趨勢，遞增率2 475 N/100(N·S/mm)；在200～800 N·S/mm區間增大時，碰撞力最大值整體呈現急劇遞增趨勢，最大遞增量30 706 N/100(N·S/mm)。

圖5 粘性阻尼系數與碰撞力關系曲線

表2 不同粘性阻尼系數下的碰撞力特征值

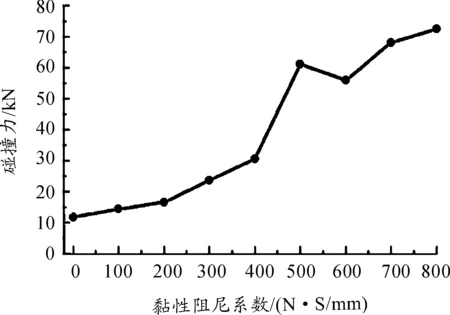
圖6 粘性阻尼系數與碰撞力特征值關系曲線

3.2 分度輪輸入轉速影響

為研究分度輪輸入轉速對于分度機構動力學特性的影響，在接觸阻尼系數100 N·S/mm、嚙合間隙0.1 mm時，分度輪轉速分別取200、250、…、550、600 r/min。從圖7得出，隨著分度輪轉速的增大，碰撞力曲線規律變化不明顯，尖點毛刺幅值增大。提取出不同分度輪轉速的最大碰撞力特征值如表3所示，并繪制出圖8所示的曲線，可知：隨著分度輪轉速的增大，碰撞力最大值呈現近似線性遞增趨勢，遞增率2 475 N/50(r/min)。

圖7 分度輪輸入轉速與碰撞力關系曲線

表3 不同分度輪輸入轉速下的碰撞力特征值

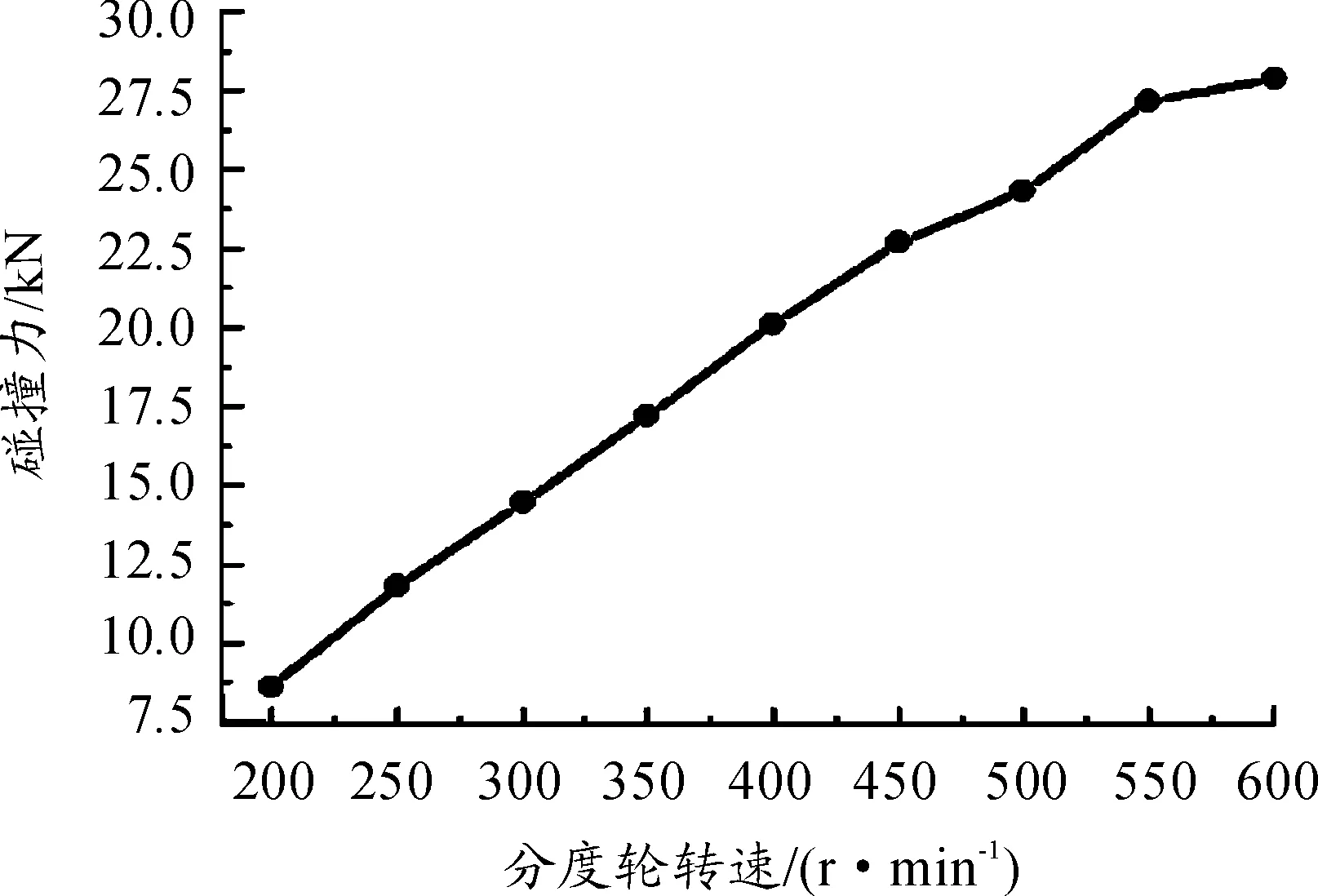
圖8 分度輪輸入轉速與碰撞力特征值關系曲線

3.3 嚙合間隙影響

為研究嚙合間隙速對于分度機構動力學特性的影響，在粘性阻尼系數100 N·S/mm、分度輪轉速300 r/min時，嚙合間隙分別取0.1、0.2、…、0.9、1 mm。從圖9得出，隨著嚙合間隙的增加，碰撞力初始位置變化復雜，碰撞力曲線在0.5 mm間隙處出現急劇增大趨勢。提取出不同嚙合間隙的最大碰撞力特征值如表4所示，并繪制出圖10所示的曲線，可知：碰撞力最大值隨嚙合間隙增大整體呈先較低值穩定、后急劇增加減小、再較高值穩定的趨勢。嚙合間隙在0～0.4 mm區間增大時，碰撞力最大值穩定在12 860～14 475 N區間；嚙合間隙在0.4～0.7 mm區間增大時，碰撞力最大值呈現先急劇增大后急劇減小趨勢，碰撞力最大值71 481 N；嚙合間隙在0.7～1 mm區間增大時，碰撞力最大值穩定在20 127～24 434 N區間。

圖9 嚙合間隙與碰撞力關系曲線

表4 不同嚙合間隙下的碰撞力特征值

圖10 嚙合間隙與碰撞力特征值關系曲線

4 結論

1)在其他參數固定的情況下，鏈式自動炮分度機構碰撞力最大值隨粘性阻尼系數增大整體呈先緩慢、后急劇遞增趨勢；隨著分度輪轉速的增大，碰撞力最大值呈現近似線性遞增趨勢；隨嚙合間隙增大整體呈先較低值穩定、后急劇增加減小、再較高值穩定的趨勢。

2)鏈式自動炮分度機構參數范圍選取粘性阻尼系數0～200 N·S/mm、嚙合間隙0～0.4 mm、分度輪輸入轉速200 r/min時，碰撞力最大值相對較小，即對其供/輸彈運動的準確性和可靠性的影響較小。