優化學習內容，激發數學學習活力

陸潔

摘? 要：小學數學教學中，教師深潛教材之中，對教學內容展開深度解析，在教學設計時細謀認知起點，探究教材內涵，精設課堂訓練，都能夠助力學生個性學習認知的成長。在教學實踐中，教師還要有意識地整合教學內容，針對學生認知基礎進行科學調度，這樣才能成功啟動學生數學思維，形成嶄新課堂教學增長點，有效激發學生學習數學的活力。

關鍵詞：小學數學;優化內容;激發活力

小學生的數學學習本身就是一個生動活潑、富有個性的學習。因此，在教學中教師就得關注學生的個性差異，并以此來精準謀劃教學活動，從而使數學學習活動得以優化，進而激發學生的學習活力，讓數學教學神采奕奕，讓學生的數學學習熱力不減 [1]。同時，教師還得審時度勢，精準研讀文本，把脈學生，優化學習內容，使學生的個性得以彰顯，幫助學生積累較為厚實的數學活動經驗，讓學生的思維得到發展，讓數學素養獲得應有的提升。

一、細謀認知起點，助力個性顯現

我們深知，找準學生的最近發展區是實現有效教學的最基本的著力點。因此，在小學數學教學中，教師就得細究新知學習的基礎，找準知識間的連接點，從而優化學習活動，采用有利于學生參與學習活動、積累活動經驗的措施，讓他們的學習更加投入，讓他們的個性得到應有的釋放。

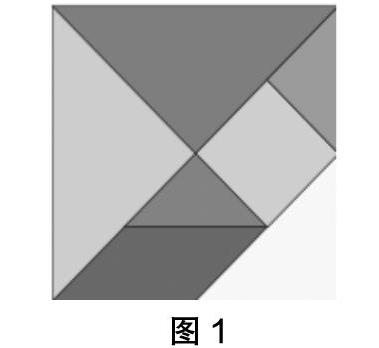
如，在“有趣的七巧板”教學活動中，教師就得深究“七巧板”的數學文化史，明白七巧板的真正價值——它是中國傳統的智力玩具，也被稱為“唐圖”。它能夠拼成各式各樣的圖形，讓學生在變與不變中發揮想象力，凸顯個性思考，顯現個性學習的魅力。同時，教師還得細細考量學生的文化基礎、經驗基礎與思維基礎，并以此為基礎激發學生的學習活力，誘發學生學習個性的展露。

師：誰知道這是什么？（圖1）

生：七巧板。

生：我玩過，可以隨意拼的。

……

師：說說你認識的七巧板中的圖形。

生：有三角形、平行四邊形、正方形三種圖形。

生：大三角形有2個，中三角形有1個，小三角形有2個，1個正方形，1個平行四邊形。

……

師：真了不起！你能從中選兩個拼一拼嗎？動手試一試。

學生活動，有的用兩個完全一樣的三角形，拼成了正方形、平行四邊形、三角形;有的則用1個平行四邊形和1個三角形拼成梯形。

師：如果讓你選3個圖形呢？你會拼嗎？

學生在自主探究的基礎上拼成了不同的圖形（如圖2）。

……

七巧板知識可謂源遠流長，具有深厚的文化底蘊。為此，在教學中教師一方面要深究七巧板所蘊含的文化，另一方面還得關注學生七巧板活動的經驗差異，學會搭建不同層次的平臺給學生學習研究的機會，也為學生個性凸顯搭建舞臺。案例中，教師創設的一看、二說、三創造的活動體系，能夠幫助學生進一步了解七巧板的構造，喚醒他們已有的七巧板拼圖經驗，從而為他們創新使用七巧板進行學習提供支持。這樣的設計能更好地貼近學生實情，貼近學習的需求，讓孩子們探究七巧板奧秘的信心更足，創造力更為旺盛。

二、深究教材內涵，助推個性生長

深究教材是教師的基本功，也是打造有效教學的基礎性工作。為此，在教學中教師就得讀通、讀透、讀細教材，科學地遴選教學內容，優化學習活動及教材組合，從而讓教學預設更貼近學生的生活實際，接近學生的知識積累，使學生在學習活動中的個性得到保護，也得到應有的生長 [2]。同時，這也讓學生的數學思維獲得應有的發展，讓學生的活動經驗積累得以豐富。

如，在“圓的周長計算”教學中，為進一步引導學生鞏固圓的周長計算，并學會運用這部分知識去解決問題，教師就得創設更多的應用情境，引導學生在具體的問題研究中理解圓的周長意義，掌握圓的周長計算，從而實現學習的突破、學習積累的提升。

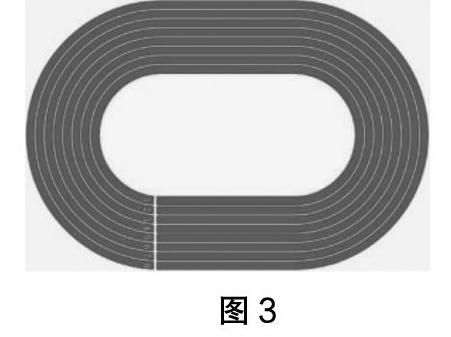
師：剛才大家對圓的周長計算得非常好！下面的場景熟悉嗎？（圖3）

生：學校操場上的跑道圖。

師：是的！你知道它的構成嗎？

生：中間黃色的部分，可以看成是由中間一個長方形，左右各是半圓組成的。

生：其他的跑道圈也是這樣的，中間都是一個長方形，左右都是兩個一樣的半圓。

師：你們的思考很正確。那下面老師就考考你們，體育老師想請你們給這個400米的跑道畫出400米比賽的起跑線，你們有辦法嗎？

生：這個跑道哪里是400米啊？

師：你的問題很好，這個跑道最里面那個黃色部分的周長是400米。

生：我們還得知道黃色部分的直徑是多少米吧？

師：有道理。我們操場最里面的長方形長121.5米，寬50米。算算它的周長是多少米？

生：這個簡單，左邊的半圓弧長π×50÷2=25π（米），右邊的半圓弧長π×50÷2=25π（米），上下的就是長邊，即121.5×2=243（米），所以跑道長25π+25π+243=400（米）。

生：這個算好了，所以第一道的起跑線和終點都是在一起的。但是要確定第二道的起跑線在哪里，好像還缺少一個條件？

生：是的，我們還得知道跑道的寬度是多少。

師：你們真了不起。通常操場跑道的寬度是1.25米，現在你能確定了嗎？

……

生：我發現，思考其他跑道的起跑線時，不需要考慮長方形的兩條長邊，只需要考慮左右半圓弧的長度變化。

生：是的，只要考慮整個圓的周長變化就可以了，跑道寬1.25米，就是半徑增加1.25米，那么直徑就增加2.5米，周長總長必定會增加2.5π米。

生：哦！我明白了，從第一條起跑線開始，每一個跑道都比前一個多2.5π米。

……

學習是什么？是一種體驗，也是一種思考，更是一種探索，同樣還是一種個性的飛揚。案例中，學生從分析組合圖形的周長開始，到只看左右半圓弧，再到看整個圓，最后被學生提煉出公式性的結論——依次向前增加2.5π米，這樣的探究歷程讓學生更富靈性，也讓學生的個性思考得以彰顯，顯現出數學學習的魅力。

由此可以看出，教師得學會做智者。案例中，教師沒有刻意地讓學生去做習題，而是把問題融合在具體的、熟悉的情境中，讓學生看圖，說構造想問題等活動讓學習成為一體。同時，學生會在教師的問題的引領下再讀圖，探尋需要解決問題的數學信息，這樣那些有價值的信息被一一篩選出來，為他們個性思考提供必要的素材。同樣，這也為學生解決同類問題提供了數學模型，讓學生的數學活動經驗得到應有的積累。

三、精思拓展練習，助力個性彰顯

拓展性練習是培養學生應用意識與創新意識的有效舉措。所以，在教學中教師就得善于創設拓展性作業，為學生應用經驗提供平臺，為學生創造性學習提供機會。同時，在教學中教師要關注學生的個體差異，特別是個性化思考能力方面的差異，鼓勵學生質疑問難，引導學生創新求異，從而讓他們在拓展性的實踐訓練中進一步彰顯個性化的思考，讓數學學習充滿智慧，洋溢著個性色彩。

如，在“長方形、正方形的面積計算”教學中，教師就得善于設計一些開放式的練習題，讓學生在具體的應用中學會思考，學會應用個性化的經驗去探尋解決問題的路徑，讓數學學習精彩不斷。

師：下面請同學們研究思考這樣一個問題——林大爺準備用120米圍欄圍一塊菜地。你能幫他設計一下菜地的形狀，算一算菜地的面積嗎？

生：簡單，設計一個長方形菜地，既整齊又方便。比如，長40米，寬20米，面積是600平方米。

生：這個不方便，還不如正方形簡單。120÷4=30（米），這是邊長，面積就是30×30=900平方米，比長方形的面積還大，又好看，方方正正的。

生：長方形的菜地還有其他的圍法。長41米，寬19米也行。

生：噢！這樣也可以的話，那長42米，寬18米也是可行的。

……

生：我發現了更好的方法，只要長與寬相加的得數是60米，就一定能圍成長方形的菜地。

生：是的，因為長+寬=周長÷2，所以只要滿足長+寬=60米，就一定能圍成長方形。

……

生：我覺得要使圍成的面積最大，不妨利用一面墻，那樣會更好。

師：又是一種新思考，接著想下去，那什么樣的情況面積最大？

……

生：經過計算，我們發現圍成正方形時面積最大。不能圍成正方形時，長與寬越接近，面積就越大。

從案例中不難看出，只要教師把握好自己的角色，切實做好學生學習的引導者、引領者，學生必定能釋放出個性學習的魅力，讓數學學習生動有趣，充滿靈智。案例中，教師設計開放式練習，只給學生120米的圍欄，讓學生學習運用知識、經驗去思考、研究，從而讓他們在不同思考的碰撞中實現學習的飛躍，學生從自然想到的，到有規律地列舉，使得數學學習走向理性的殿堂，同時也讓學生的個性化學習得以張揚。

數學學習的目的就是讓學生聰明起來，讓學生的數學活動經驗不斷豐富起來，讓學生的數學思維愈加敏銳起來。所以在小學數學教學中，教師就得善于創設問題情境，優化數學學習活動，從而激發學生進行個性化思考與研究，讓他們的學習更富智慧，讓他們的數學素養獲得充分的發展，同時也讓我們的數學教學更具神韻，洋溢著智慧的氤氳。

參考文獻：

[1]? 吳春梅. 變易理論與小學數學教學[J]. 數學教學通訊，2018（16）.

[2]? 陳清容. 把握內容要素 確定教學方向——小學數學教學內容要素的實踐研究[J]. 小學數學教師，2018（11）.