基于協整理論的新疆消費水平實證研究

林 杉

(西安財經大學 陜西 西安 710100)

一、緒論

(一)選題的背景和意義

本論文通過建立一個符合社會主義市場經濟特色和新疆地區發展特色的宏觀經濟模型，全面描述國民經濟各領域簡單的相互關系及相互影響。本文主要針對居民消費模塊進行研究，通過協整檢驗理論，建立誤差修正模型和向量自回歸方程體系，這是年度宏觀經濟模型的重要組成部分。

二、新疆居民收入與消費協整關系的實證分析

(一)數據來源與說明

本文對新疆維吾爾自治區1994-2014年間宏觀經濟中的消費模塊進行實證分析，主要針對消費與收入的關系進行研究，試圖通過協整分析來判斷收入與消費是否存在長期穩定的均衡關系。由于城鎮居民和農村居民的收入消費函數存在較大的差異，故本文將居民消費分為城鎮居民消費和農村居民消費兩部分。

本文的數據來源于歷年的《中國統計年鑒》。原始數據為1994-2014年新疆城鄉居民收入與消費數據，將其剔除價格因素的影響。本文選取的統計變量有城鎮居民人均可支配收入(YUR)、農村居民人均純收入(YRR)、城鎮居民人均消費支出(CUR)、農村居民人均消費支出(CRR)。由于各變量數據不全都是平穩的，為增強其平穩性，并消除可能存在的異方差現象，我們對選取的數據進行取自然對數處理，處理后上述變量分別設為LYU、LYR、LCU、LCR，對數變化不會改變原變量之間的協整關系。

(二)協整理論與誤差修正模型的實證分析

1.平穩性檢驗(單位根檢驗)

本文基于單位根檢驗原理，利用Eviews6.0軟件采用ADF方法對各變量及其差分變量進行單位根檢驗，其檢驗結果如下表1。

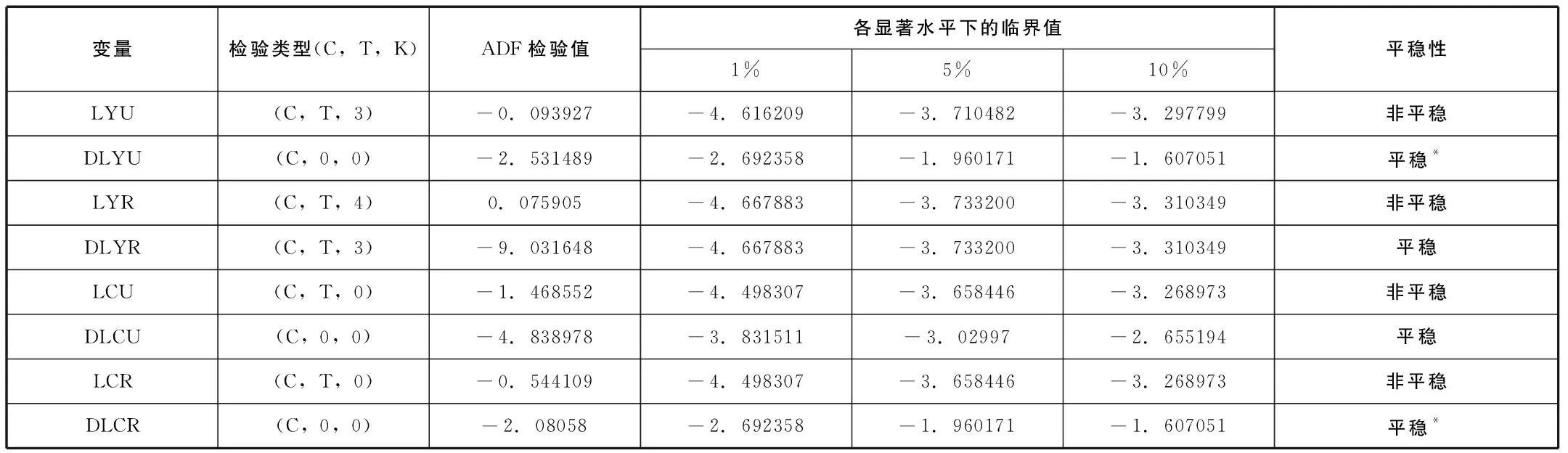
表1 各變量及其差分變量的單位根檢驗統計表

由表1的結果分析知，上述所檢驗的變量均為非平穩變量，即均有單位根的存在，故需對各變量進行差分并繼續利用ADF法進行檢驗差分后各變量的平穩性。

2.協整關系的檢驗

根據依據上一節變量的單位根檢驗結果發現，在5%的顯著水平下，LYU與LCU、LYR與LCR均為I(1)變量，由于同階單整變量之間可能存在協整關系，故在檢驗協整關系時只需要檢驗LYU與LCU、LYR與LCR的協整關系。構造的協整方程具體如下：

(1)城鎮居民消費與收入的潛在協整方程為：

LCU=-0.225384+0.996167LYU

t值：(-2.506993)(100.1782)

(2)農村居民消費與收入的潛在協整方程為：

LCR=0.061892+0.965713LYR

t值：(0.229353)(28.18165)

δt=LCR-0.061892-0.965713LYR

(3)誤差修正模型(ECM)

通過軟件擬合得到誤差修正模型及其相關檢驗量和擬合指標如下：

ΔLCUt=0.003706+0.954634ΔLYUt-1.191605ecmt-1

(0.313335) (9.183232) (-5.0165)

此時得到殘差是否自相關檢驗的結果與滯后期的結果如表2所示：

表2 誤差修正模型殘差自相關檢驗結果

顯然，直到滯后5期的殘差自相關檢驗結果都表明殘差是不相關的，因此上述誤差修正模型是合理的。

上述誤差修正模型顯示，城鎮居民的消費短期波動一方面受到收入的短期波動影響，影響程度為0.954634，但并不受到消費和收入差分滯后期的影響，因此這種影響是沒有滯后效應的。城鎮居民的消費短期波動另一個影響就是反應在誤差修正模型的修正項ECM中。對于兩個變量的誤差修正模型來說，誤差修正想系數一定顯著為負，從而實現偏離均衡的調整機制，其系數反映了變量波動偏離長期均衡時的調整速度與能力。就本文的實證結果而言，新疆城鎮居民的誤差修正指數為-1.191605，相對于短期波動的系數而言，調整速度和力度相當強烈。

三、居民消費向量自回歸模型(VAR)體系的構建

(一)模型變量的設定

本章具體就消費、收入、價格以及金融的關系利用向量自回歸的理論建立相應的VAR模型體系，所選取的內生變量有城鎮居民人均消費(LYU)、農村居民人均消費(LYR)、城鎮居民人均可支配收入(LCU)、農村居民人均純收入(LCR)、城鎮居民消費價格指數(LCPIU)、農村居民消費價格指數(LCPIR)。

(二)模型的構建

1.單位根檢驗

表3 各變量的單位根檢驗結果表

由表4-1結果分析知，上述的兩種價格指數變量均含有單位根，即為非平穩變量。進一步檢驗非平穩變量的一階差分的平穩性可得：在1%的顯著水平下，兩個變量都為一階單整變量，即I(1)變量。結合上一章的單位根檢驗結果知，LYU、LCU、LCPIU均為I(1)變量，LYR、LCR、LCPIR也為I(1)變量，這滿足協整關系的前提條件。

2.協整檢驗

表4 城鎮的VAR模型各個標準與滯后期的關系

表5 農村的VAR模型的各個標準與滯后期的關系

注：*表示該信息指標下應該選擇的階數

上一章中對協整關系的檢驗采用的方法是EG兩步法，這種方法只適用于單方程的協整關系的檢驗，而本章的兩個模型中均含有三個變量，故不能繼續采用EG法進行檢驗，本章采用Johansen和Juselius的特征根跡檢驗(trace檢驗)和最大特征值檢驗兩種方法進行檢驗。JJ法不僅檢測出變量之間是否存在協整關系，而且能夠確定出協整變量的個數。具體檢驗結果如表6、表7所示：

表6 城鎮消費體系中各序列協整檢驗的結果

注：**表示在1%的顯著水平下拒絕原假設

表7 農村消費體系中各序列協整檢驗的結果

注：*表示在1%的顯著水平下拒絕原假設

由表3、表4知，在1%的顯著水平下，變量LYU、LCU、LCPIU三個變量之間存在協整關系，且只有一個協整向量；在1%的顯著水平下，變量LYR、LCR、LCPIR、三個變量之間也存在只有一個協整向量的協整關系，這為VAR模型建立的合理性提供了前提。

3.VAR模型的構建

(1)城鎮居民消費VAR(1)模型：

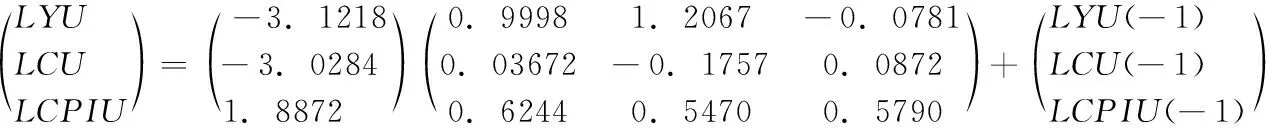
(2)農村居民消費VAR(3)模型：

模型整體檢驗結果如表8。從整體檢驗結果來分析，兩個模型的AIC和SC值都很低，擬合的效果也都很好，故可以進行預測。

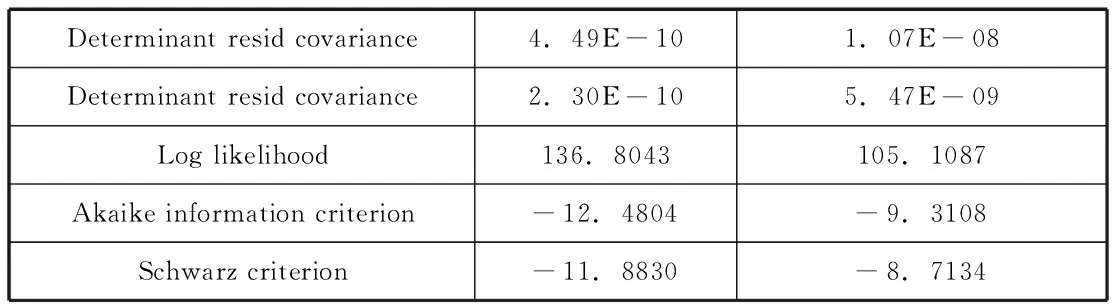
表8 居民VAR模型的整體檢驗結果

(三)VAR模型的模擬與預測

1.對歷史數據的模擬

為了更加客觀地描述模型的預測能力，本文將先采用“樣本內預測”的方式，針對1994-2014年進行“預測”，依據上一節求解的VAR模型，對各變量的殘差進行分析，得出相對誤差表。即對已知的歷史數據進行預測，得出的預測值與我們所知道的真實值進行比較，得出模型的預測誤差，預測的相對誤差(預測誤差/實際值)如表9所示，由此可評價模型的預測能力，這樣做的好處是不需要花費更長的時間等待新數據的產生。

表9 居民消費VAR模型預測絕對誤差表 (單位：%)

由表4-8知，城鎮居民人均消費的最大預測誤差約為0.963%，城鎮居民人均可支配收入的最大預測誤差約為1.078%，城鎮居民消費指數的最大預測誤差約為1.039%。同理，由表4-9知，農村居民人均消費的最大預測誤差約為0.855%，農村居民人均純收入的最大預測誤差約為1.906%，農村居民消費指數的最大預測誤差約為3.171%。由此可見，除了城鎮居民人均消費的預測效果低于農村居民人均消費之外，其它兩項指標的預測最大誤差都是城鎮消費體系的指標較低。總體來說，所有指標的預測的最大誤差均在5%以內，因此預測誤差整體滿足要求，這說明模型的短期預測能力很高，可以進行預測。

四、結論與建議

可以采取措施來改善人民的消費觀念的差異，逐步改善農村經濟結構及農村設施，大力發展旅游業，豐富農民收入來源，充分提高農民的收入，同時，加大對農業發展的扶持力度，降低農民對農業生產投資的風險度。為進一步促進城鎮居民消費水平的提高，政府可放寬買房、買車的限度，完善社會保障體系及信用體系，提高中低層收入者的工資水平，促使人們將儲蓄轉化為消費。