探測器故障下醫用CT圖像重建的容錯算法開發

董 建，畢丹陽，楊耿煌，秦轉萍

（1.天津職業技術師范大學天津市信息傳感與智能控制重點實驗室，天津 300222；2.唐山工業職業技術學院自動化工程系，唐山 063299）

計算機斷層成像（computed tomography，CT）技術具有適用面廣、分辨率高、對比度好、價格相對低廉等優勢，已成為使用最廣泛的無創臨床成像技術之一[1-2]。自1979年我國引入第一臺醫用CT 以來，CT 設備已經在我國各級醫院工作了40年，早期投入使用的設備正相繼進入設備老化和故障期[3-4]。X 線探測器是CT設備的核心部件，也是故障高發部件。探測器故障會導致CT 圖像出現環狀偽影，嚴重影響正常組織結構和病變區域的刻畫[5-6]。而現階段我國CT 研發及設備維護技術團隊已經無力應對各醫療機構集中出現的設備故障問題，研發具有容錯機制的CT 圖像重建算法已經迫在眉睫。據本團隊了解，還未發現國內做相關研究的報告，本文提出的探測器故障下的CT 圖像重建的容錯算法開發尚屬解決此類問題的首例研究。

本文提出一種在未知探測器受損數量和具體位置信息的故障條件下，依然能夠精準重建的CT 圖像重建算法。傳統的迭代式重建算法采用正向投影與實測投影數據的最小二乘差，即L2 范數差作為最小化評價函數[7-8]。眾所周知，L2 范數對實測投影數據的異常值尤其敏感，這決定了此傳統方案無法避免CT 圖像中環狀偽影的出現。而一種能有效預測異常值位置并將其精準濾除的方案，即采用L1 范數為最小化評價函數。基于這一想法，開發了一種類似于代數式重建法（algebraic reconstruction technique，ART）的行處理型（row-action-type）迭代式重建算法[9-10]，該算法由凸優化領域的近端分裂理論（proximal splitting）推導構建而成[11-12]。此外，通過向L1 范數追加全變分（total variation，TV）懲罰項[13-16]，新算法在去除環狀偽影方面更具魯棒性。在經典Shepp-Logan 模型重建實驗以及實際臨床CT 圖像的重建實驗中，新算法較傳統L2 范數重建算法表現出顯著優越性。

1 算法介紹

1.1 問題定義

CT 設備獲取人體斷面圖像的掃描過程如圖1所示。

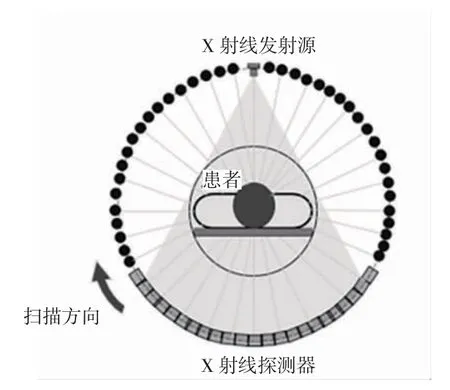
圖1 CT 設備獲取人體斷面圖像的掃描過程

重建一張人體斷層圖像，CT 設備需要對該斷面進行1 000～1 500 次X 射線掃描。在X 線的某一通路上，令X 線源發出的X 線的強度為I0，探測器接收到的被人體部分吸收后的X 線的強度為I1。在不考慮噪聲影響的前提下，I1與I0存在如下等式關系

式中：b 為投影數據；γ 為探測器對X 線的靈敏度。探測器正常工作條件下γ = 1，若探測器出現故障，則γ→0。此時投影數據b 為

即探測器故障情況下，測得的投影數據值遠小于探測器正常工作條件下的測得值。重建圖像中環狀偽影的產生機理闡述如下：在圖像重建的反投影這一關鍵步驟中，受損害的投影數據使得該通路上的各像素由于得不到有效恢復而取值大幅減小。此外，根據重建規則，反投影運算會在各角度方向依次進行，進而使得無法恢復正常取值的像素在某一路徑進行重合。180°的反投影運算使得該路徑逐漸演變為半圓形結構，而且重合次數足夠多的像素取值偏大，重合次數少的像素取值偏小。該半圓形結構即對應重建圖像中由相鄰的亮區和暗區所組成的環狀偽影。完整、1 個和2 個探測器故障的投影數據與相應濾波反投影算法（filtered back-projection，FBP）的重建圖像如圖2 所示。

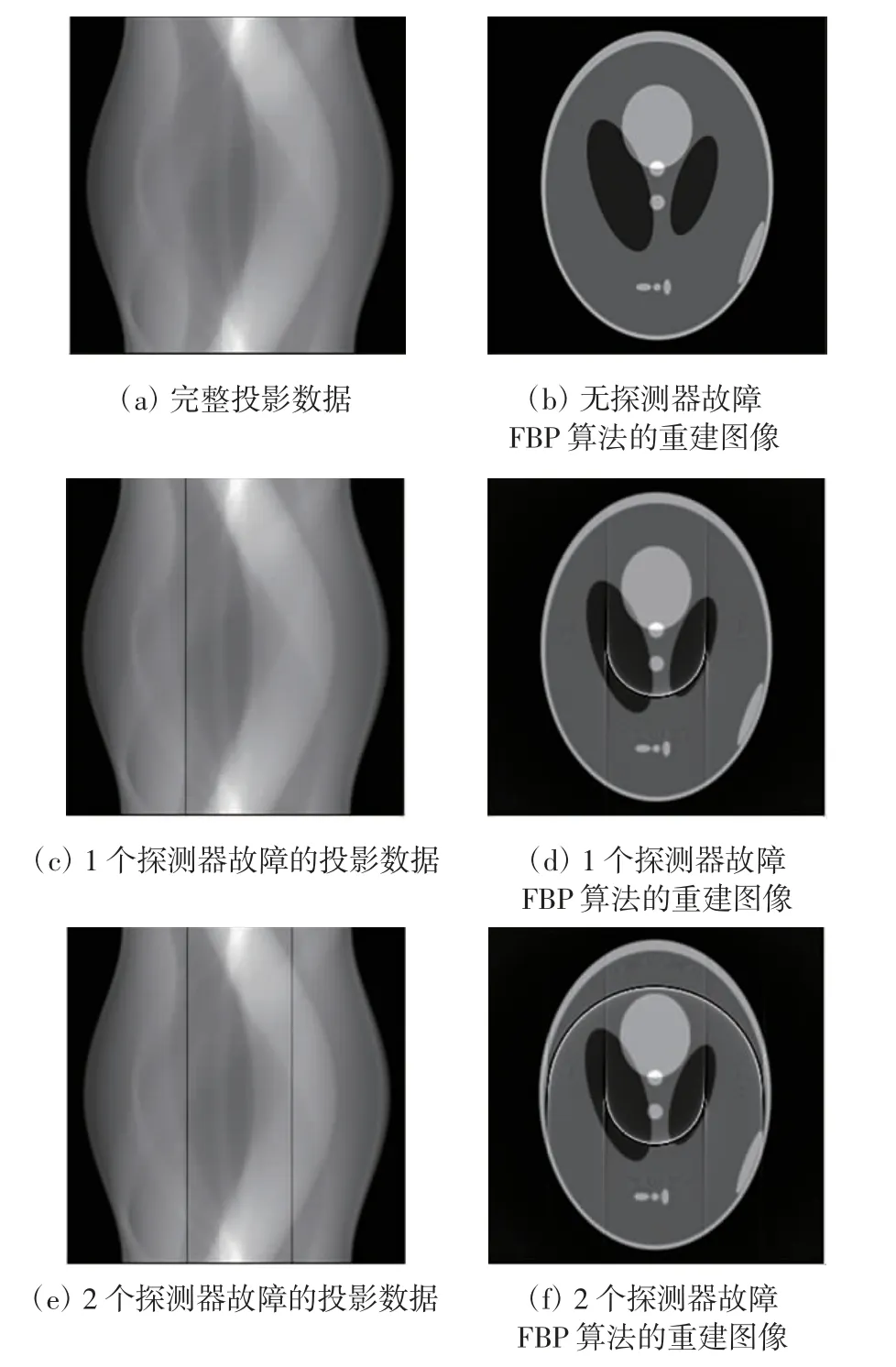
圖2 完整、1 個和2 個探測器故障的投影數據與相應FBP 算法的重建圖像

探測器無故障和隨機性出現1 個和2 個探測器故障時，由一般商業CT 搭載的FBP 算法重建了經典Shepp-Logan 模型。由圖2 可知，完好投影數據可重建出理想圖像，探測器故障可引起投影數據的某一列數據異常，進而導致重建圖像中的環狀偽影。偽影出現個數與出現故障探測器個數一致。

CT 圖像重建即利用重建算法將投影數據轉化為CT 圖像的過程。迭代式重建算法可將問題定義為求解多元線性方程組 Ax = b 的問題，此處 x =（x1，x2，…，xJ）T為J 維未知量即待重建的CT 圖像，b=（b1，b2，…，bI）T為I 維已知量即實測投影數據，A={aij}為I×J 維系統矩陣[17-18]。本文研究I≥J 的超定方程組求解問題。迭代式重建領域的標準評價函數為L2 范數差

本研究將傳統L2 范數置換為L1 范數，如式（4），并通過將f（x）最小化而推導出行處理型迭代式重建算法。

2 種范數差展開式表示為

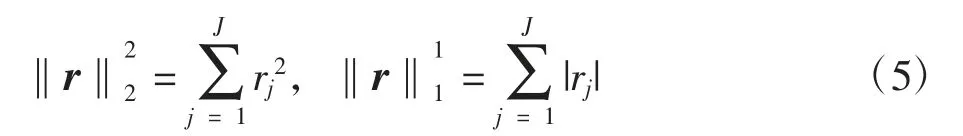
1.2 近端分裂理論

在實施算法推導前，有必要先對其基礎內容的近端分裂理論及其對算法推導的重大貢獻做簡要介紹。首先考慮以下凸優化問題

假定式中f（x）為可能不可微分的下半連續凸函數。近端算子法（proximal operator）為求解此類最優化問題提供了良好解決方案。對應于f（x）的近端算子表達式為

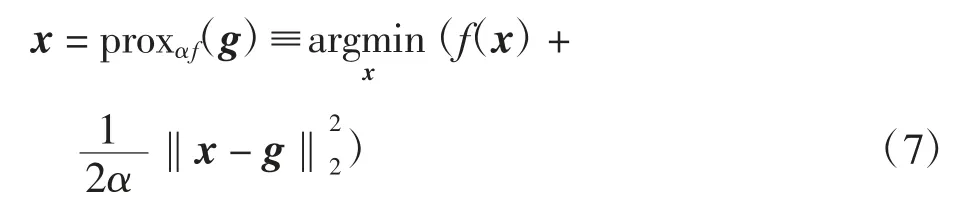
式中：α 為步長參數。

近端算子具備2 種優秀屬性。

（1）它可針對任何一個下半連續凸函數進行定義，即使該函數不可微（如L1 范數）；

（2）在步長參數α ＞0 的前提下，滿足x=proxαf（g）的定點x 與使凸函數f（x）取最小值時的變量x 相一致。

這2 個性質決定了可以應用如下迭代式求得凸函數f（x）取得最小值時的變量x

式中：k 為迭代次數。

該迭代算法叫做近端最小化算法，它為不可微凸函數的最優化問題提供了強有力的解決方案。

凸函數f（x）可拆分成若干分量函數fi（x），即其中fi（x）（i=1，2，…，I）均為可能不可微但滿足下半連續的凸函數。此時，假定凸函數f（x）的近端算子求解難度巨大，而其各個分量函數fi（x）的近端算子能夠由低計算成本求得。近端分裂理論能夠為該條件下的凸優化問題提供解決方案，它的處理方式為在求解由x(k)到x(k+1)的過程中，進一步將問題分解為按照i=1，2，…，I 的順序進行各分量函數所對應的近端算子的計算，即

當 i=I 時，x(k+1)=x(k，I+1)。

式中：k 為主循環變量；i 為子循環變量。

步長參數α(k)值會隨k 值改變。為了使所求解序列x(k)收斂于函數f（x）取最小值時的變量x，α(k)需滿足如下條件[12]

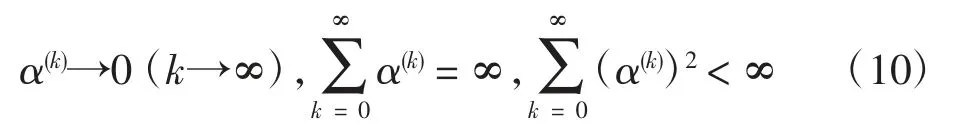
近端分裂理論為本文L1 范數重建算法的構建提供了理論依據。

1.3 L1范數重建算法描述

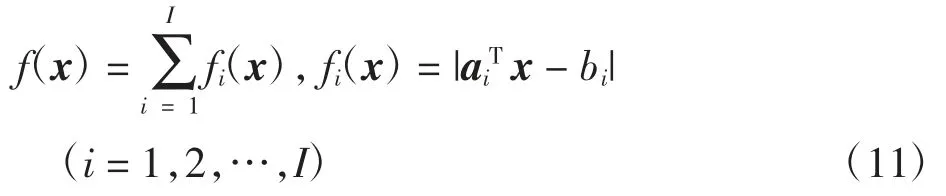
式中：ai為系統矩陣A 所對應的第i 行分量。進而求解各分量函數所對應的近端算子，即求解以下最優化問題

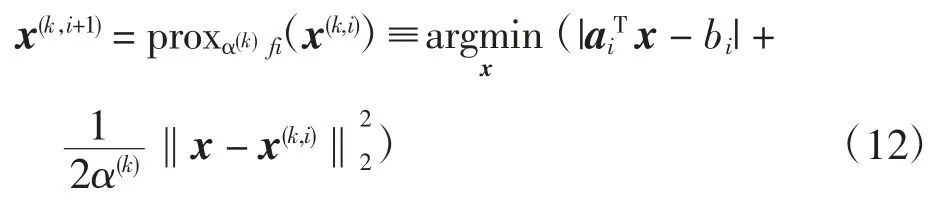
該近端算子的計算可由拉格朗日乘子技術簡單求得。首先，引入替代變量則以上問題轉變為約束極小化問題

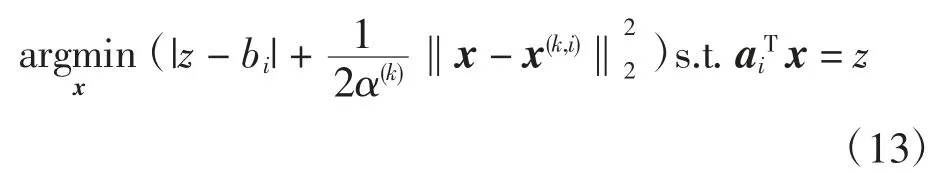
對應于式（13）的拉格朗日函數可定義為

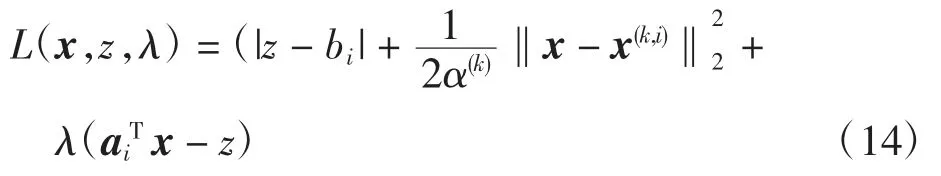
式中：λ 為拉格朗日乘子，也稱作對偶變量。

對應于式（14）的對偶問題可定義為

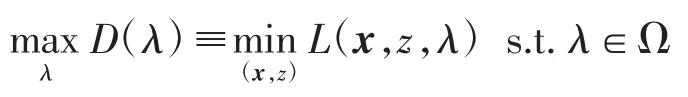
通過對該對偶問題的求解，可得到未知解x 的更新公式為

同時可得到對偶變量的表達式及取值范圍

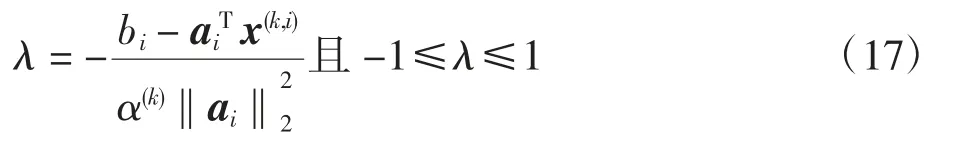
可將λ 分情況表示為

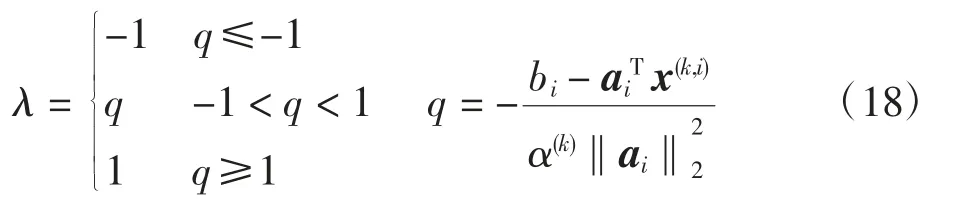
將式（18）代入式（16），即可得到 x(k,i)的更新解x(k,i+1)=proxα(k)fi（x(k,i)）。由于步長參數α(k)需滿足隨循環變量k 而遞減的條件，故將其設定為

式中：α0＞ 0，? ＞ 0 為提前給定的正數常量。

至此，L1 范數重建算法已經構建完成。

1.4 L1范數重建算法

步驟0設定步長參量α0和? 的初始值，為變量x 取初值 x(0，1)，以 k=0，1，2，…的順序執行步驟 1 到步驟3；

步驟1計算步長參數

步驟2以i=1，2，…，I 的順序執行以下操作：

①計算λ

②更新x

步驟3x(k+1,1)=x(k,I+1)

為了得到更好的圖像重建效果，進一步向L1 范數的評價函數中追加了全變分懲罰項‖x‖TV，定義如下

式中：xm，n為在一幅二維圖像中坐標為（m，n）的像素的像素值。全變分模型是一個依靠梯度下降流對圖像進行平滑的各向異性的模型，能對圖像起到良好的去噪和平滑作用[13-16]。因此，L1-TV 重建的最小化評價函數為

式中：β 為可調節全變分作用強弱的超參數。

2 實驗結果及分析

2.1 少數探測器故障下的圖像重建

本文對經典Shepp-Logan 數字模型進行重建實驗。該數字模型所含像素數為256×256，像素值的分布范圍為[0，4.5]。圖像重建領域的常用做法是獲取與重建圖像的像素數等量的投影數據量，因此本文以[0°，180°]和 180°/256 的角度間隔進行投影數據采集，投影數據的像素數同樣為256×256。

假定出故障的探測器個數為1 個和2 個，并且假定出現故障的探測器的位置具有隨機性。分別用L2范數重建算法、L1 范數重建算法和L1-TV 重建算法對含有異常值的投影數據進行重建實驗。經實驗驗證，對于本實驗的Shepp-Logan 數據模型，在各參數取以下數值時可得到最佳重建效果。在各項實驗中α0=0.03，?=50，L1-TV 實驗中 β =260。各項實驗的迭代次數k 設定為100。在不同探測器故障個數條件下各算法的實驗結果如圖3所示。其中，圖3（a）、（c）、（e）為 1 個探測器故障時的重建結果，圖3（b）、（d）、（f）為2 個探測器故障時的重建結果。由結果圖像可知，L2范數重建的圖像仍含有嚴重的環狀偽影，并且在半圓環偽影的起點和終點處二次產生了直線型放射狀偽影。L2 范數的重建結果與FBP 算法的重建結果的圖像效果相似。L1 范數的重建效果較L2 范數的重建效果有了顯著提高，環狀偽影得以有效去除。然而，偽影處的黑色瘢痕仍有殘留，并且圖像全體可見微弱的直線型偽影。L1-TV 算法得到了最好的重建效果，圖像中的環狀偽影得以完全去除，并且各組織結構的灰度得到了有效的平滑。

2.2 多數探測器故障下的圖像重建

本文進一步設計了條件嚴苛的驗證實驗，即假定探測器的故障個數為9 個。各項實驗中的參數取值不變。9 個探測器故障條件下各算法的無噪聲影響和有噪聲影響的重建結果如圖4所示。圖4（a）、（c）、（e）為在無噪聲影響下用各種范數進行圖像重建的實驗結果。由結果圖像可知，嚴重的環狀偽影分布于整幅L2范數的重建圖像，并且在環狀偽影的起點和終點處存在顯著的直線型偽影。圖像的某些細節信息被偽影覆蓋，并且高灰度值的環狀偽影降低了圖像原有信息的對比度。在L1 范數的重建圖像中，高灰度值的環狀偽影被有效去除，并且在環狀偽影的起點和終點處的直線型偽影也被完全去除。圖像的細節信息得到了較好的保存。然而，在L1 的結果圖像中，仍有暗黑色環狀偽影瘢痕殘留。L1-TV 算法得到了最佳實驗效果，偽影被完全去除，圖像細節保存完好，并且各組織結構均勻一致。鑒于CT 圖像采集過程中會受到電子噪聲的影響，為了使該實驗更接近實際運行機制，在投影數據中加入了均值為0、方差值為6.0 的高斯噪聲和發射光子數為5.0×105條件下的泊松噪聲。各項實驗中其余參數取值不變，為控制統計噪聲將循環次數k設定為 200。圖4（b）、（d）、（f）為在 2 種噪聲影響下用各種范數進行圖像重建的實驗結果。在L2 范數的重建圖像中充滿了亮暗并存的環狀偽影以及統計噪聲，環狀偽影與物體邊緣交界處可見部分組織結構變形。L1 范數重建充分去除了環狀偽影的明亮區域和部分統計噪聲。L2 范數重建中的部分組織結構變形得以恢復。L1-TV 算法有效去除了環狀偽影和統計噪聲，然而由于為達到去除統計噪聲目的而進行的過度平滑使得圖像微小細節結構有所消失。

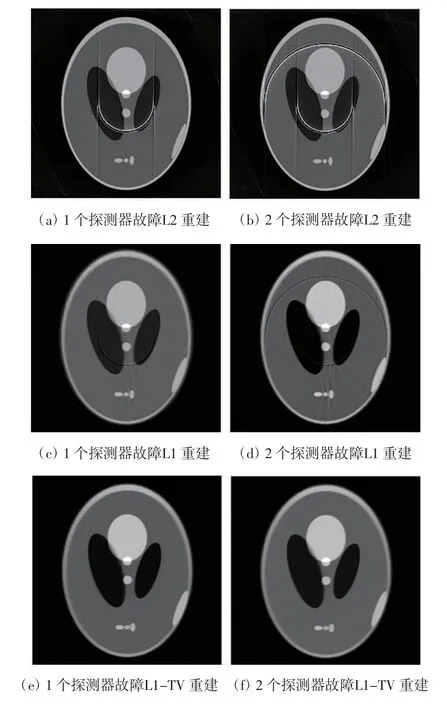
圖3 不同數量探測器故障條件下各算法的實驗結果

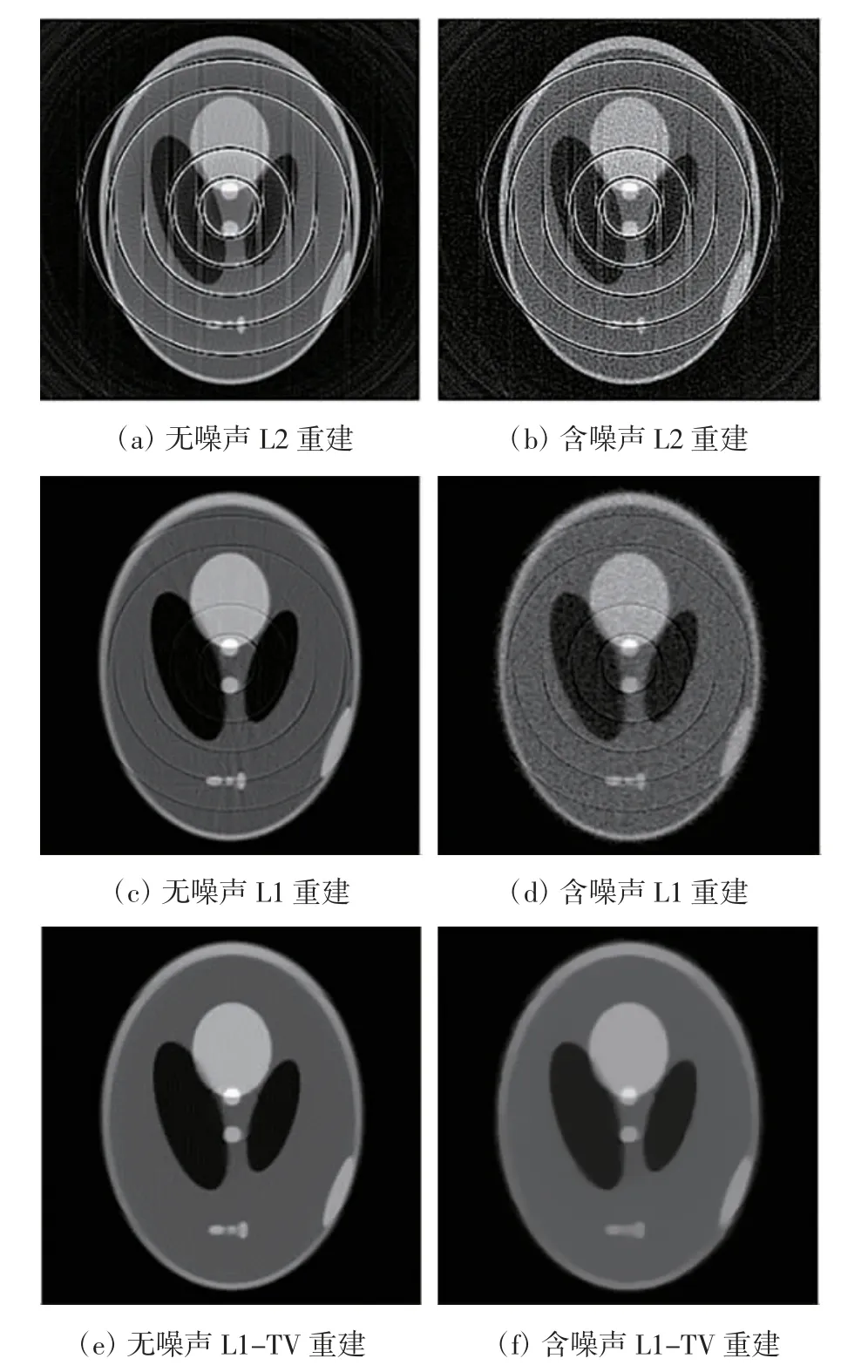
圖4 9 個探測器故障條件下各算法的無噪聲影響和有噪聲影響的重建結果

2.3 臨床CT圖像的重建

為進一步驗證算法有效性，選取了臨床中常用的上腹部CT 圖像進行了重建實驗。該圖像的像素數為512×512，像素間距為0.625 mm，因此圖像的采集范圍為32 cm×32 cm。各像素的取值為對應區域的X 線衰減系數值，像素值分布范圍為[0，0.387]。采集的投影數據像素數為512×512。各實驗參數設置如下：α0=0.002，?=50，L1-TV 實驗中 β =8 600（β 值越大，圖像的平滑效果越小）。含3 個探測器故障的上腹部CT 斷層圖像的重建結果如圖5 所示，實際圖像的重建效果與上述數字模型重建效果保持一致。L2 范數重建結果中有明顯的環狀偽影出現，而L1 范數重建有效去除了環狀偽影的明亮區域，L1-TV 重建得到了良好質量的重建圖像。

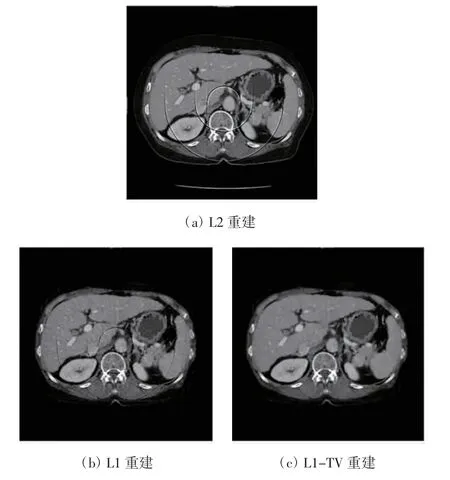
圖5 含3 個探測器故障的上腹部CT 斷層圖像的重建結果

實驗結果表明，在單個及多數探測器故障條件下L2 范數重建不能消除圖像中的環狀偽影，而L1 范數重建能有效去除高灰度值的環狀偽影，L1-TV 重建算法能夠得到良好的圖像重建效果。在受高斯噪聲和泊松噪聲影響的條件下，L1 算法依然展現出對環狀偽影去除的有效性。深究3 種算法的不同發現，L1 算法較L2 算法具有顯著優越性的原因在于圖像更新過程具備異常值濾除程序。式（16）中，λ 的取值被限定在的取值被限定在一定合理區間，該過程即決定了若投影數據bi存在異常值則會被濾除的運行機制。而L1-TV 算法較L1 算法具有優越性，原因在于全變分懲罰項能夠對圖像起到有效的平滑和去噪作用。

3 結 語

本文研究了在醫用CT 設備的核心部件X 線探測器部分損壞的條件下，進行具有容錯機制的圖像重建算法的開發問題。以經典Shepp-Logan 數字模型作為重建對象，設計了單個及多個X 線探測器出現故障情況下的重建實驗。此外，還討論了在電子噪聲影響下的重建情況以及實際的上腹部CT 圖像的重建情況。分別對比了傳統L2 范數重建算法和本文提出的L1范數重建和L1-TV 重建算法。實驗結果表明，L2 范數重建不具備去除探測器故障引起的環狀偽影的功能，其重建效果接近于當前醫用商業CT 所搭載的FBP 算法的重建效果。而L1 范數重建算法較傳統L2 范數重建在去除探測器故障引起的環狀偽影方面具有顯著優越性，能有效去除CT 圖像中光亮的環狀偽影，然而該算法在去除暗黑色環狀偽影方面還存在不足。增強算法L1-TV 算法有效彌補了L1 算法的不足，具備完全去除環狀偽影和有效保護圖像細節和對比度的能力。本文提出的探測器故障下醫用CT 圖像重建的容錯算法具有較強的容錯能力，能夠實現多數探測器同時出現故障的情況下的精準圖像重建。因此，該技術為我國各臨床機構中已經進入老化和故障期的CT 器械能夠繼續服役提供了有效的技術支撐。