“幾何畫板”融入高中數學課堂教學實踐與研究

王雪梅 李龍華

【摘要】近年來，“幾何畫板”被廣泛地應用于數學課堂，這是對傳統數學教學模式的一大突破，不僅有助于激發學生的數學學習興趣，而且可以推動教師進行教學方式的革新.教師利用“幾何畫板”進行教學，能夠將教學中的重點、難點更加直觀、形象地展示出來，能夠提高學生的學習積極性，培養學生自主探究的能力.在本文中，筆者將以高中數學課堂為研究對象，探究“幾何畫板”在高中數學課堂中的應用實踐，挖掘其輔助數學教學的深層特點.

【關鍵詞】幾何畫板;高中數學;教學實踐與研究

“幾何畫板”（The Geometers Sketchpad）是一個出色的學習和教學軟件，教師利用該軟件，可以精確地畫出各類圖像，直觀動態地演示圖像，化靜為動，營造一種真實的環境，使教學效果更加逼真，從而降低學生對數學學習的畏懼，使學生對知識、概念的理解更加清晰，同時也可以培養學生的空間想象力.“幾何畫板”在課堂中的融入，有效改善了學生的學習方式，改變了教師的教學方法，將課堂氛圍從枯燥無味轉化為生動活潑.

一、利用“幾何畫板”創設豐富的教學情境，激發學生的學習興趣

將“幾何畫板”作為數學課堂教學的輔助工具，可以大大提高教學效率.教師借助“幾何畫板”可以為學生模擬出立體圖形的三維影像，使學生的注意力集中到屏幕上，提高學生對知識的專注度并增強其好奇心，讓學生以積極愉悅的態度去對待課堂知識，主動投身于教學情境中.

例如，在教學“指數函數及其圖像”時，教師先用“幾何畫板”創設一個細胞分裂的情境，這樣的導入貼近學生熟悉的實際生活，能夠引起學生極大的興趣.通過觀察細胞分裂的過程，學生可以根據觀察得出的規律歸納出細胞個數與細胞分裂之間的數學關系，再結合有關指數函數的知識，求出函數解析式、定義域等內容，此時教師再用“幾何畫板”繪制學生剛剛求得的指數函數的圖像，能夠讓學生留下深刻的印象.

數學是同日常生活聯系密切的學科，教師若在數學教學中利用“幾何畫板”創設情境，則可以將生活同學生的學習結合起來，使學生對數學學科多幾分親切、少幾許陌生.例如，在“正弦函數的圖像”這一課的教學中，教師可以借助“幾何畫板”創設彈簧振子作簡諧振動的情境，模擬出有關生活化景象，使學生對正弦函數圖像的記憶更加深刻.學習“橢圓”這一課時，教師若利用“幾何畫板”對行星的軌跡進行模擬，則可以幫助學生去感受橢圓的應用、感悟橢圓的本質規律，學生對模擬出的畫面進行思索時能夠更深入地理解橢圓的概念，這也是“幾何畫板”在數學概念教學中的影響之一.

心理學研究表明：學生的思維活動總是由問題開始的，并在解決問題的過程中得到發展.學生學習的過程就是一個不斷提出問題，又不斷解決問題的過程，因此在教學過程中教師要不斷創設問題情境，激發學生的求知欲.教師創設問題情境，并借助“幾何畫板”為學生提供主動探索和發現問題的條件，使學生的思維能力在問題的猜想與驗證中得到提升和發展.例如，研究冪函數圖像的特征和性質時，教師創設問題情境：“同學們能否利用‘幾何畫板在同一個直角坐標系中作出函數y=x，y=x2，y=x3，y=x12，y=x-1的圖像？通過繪制的各函數圖像的形狀和位置的比較，同學們可以歸納出冪函數的性質嗎？”讓學生分小組動手操作“幾何畫板”生成函數y=xα，α是參數，隨意改變α的值，如-2，-3，-12，23，32，2，4，5等，觀察繪制出的各函數圖像，對冪函數的性質進行驗證.教師要給學生充分的時間，給他們想、做、說的機會，讓他們討論、質疑、交流，讓學生通過“幾何畫板”的輔助，揭示、驗證冪函數的圖像特征和性質結論，這樣原本靜止枯燥的數學課就會變成輕松、活潑能夠讓學生展示自我的舞臺，學生的積極性、參與度都會大大提高，從而在輕松愉快的氛圍中獲得知識.

二、利用“幾何畫板”動態展示教學內容，領悟數形結合的數學思想

在多年課堂教學實踐中我們發現：學生在學習函數的有關概念、平面解析幾何、立體幾何等有關知識時，都或多或少存在一定的學習障礙，“數”與“形”不能很好地“統一”.

數學家華羅庚說：“數缺形時少直觀，形少數時難入微”.然而，教學道具只有一塊黑板、一支粉筆式的教學在講解數形結合、圖像動態變化、空間幾何體等內容時比較困難，靜態的、粗糙的粉筆作圖很難把圖像準確地描繪清楚.對此，利用“幾何畫板”可以展示圖形變化的動態過程以及圖像變化時隨之出現的數值變化，將抽象的公式轉化為形象的圖像，把解題的過程直接呈現出來，真正意義上實現數形結合.

比如，教師用“幾何畫板”教授“直線與圓的關系”一課時，能夠把教學內容變得形象、直觀，一改枯燥無味的課堂氛圍.再如：“幾何畫板”可以用來研究線性規劃最優解的問題.例如：求目標函數z=2x+y的最大值和最小值，使式中x，y滿足下列約束條件： x-4y≤-3，3x+5y≤25，x≥1.

在實際教學中，我們發現學生在尋找最優解時常常出現一些問題：一是作圖精度不夠，很難準確畫出可行域;二是不易控制目標函數的平移，找到的最優解出現錯誤.教師借助“幾何畫板”就可以解決這些困難，“幾何畫板”不僅能夠精確畫出可行域和目標直線，還可以清晰地演示自動平移直線y=-2x+z尋找最優解的動態過程，讓學生充分體驗用圖解法求最優解的發現、探索過程，建立精準的數形聯系，使線性規劃問題的求解深入淺出，通俗易懂.

從平面圖形到空間立體圖形，是認識上的一次飛躍，很多學生學得比較吃力，跟不上教師的節奏，將“幾何畫板”融入課堂教學可以解決這個問題.利用“幾何畫板”可以在極短時間內描繪出需要的幾何圖形，甚至可以對部分重點圖形結構、輔助線等進行色彩標注，也可以選擇設置閃爍效果，使其更為突出;利用“幾何畫板”構造的立體圖形，可以旋轉，學生能夠清晰地看到圖形的多個角度，這與傳統教學方式中只能呈現圖形的一個角度顯著不同;利用“幾何畫板”可以將圖形動態變化，有利于學生深入理解幾何圖形的面積、體積公式.

三、利用“幾何畫板”進行發現式探究活動，培養學生團結協作、解決問題的能力

高中數學中有很多教學難點，為了突破教學難點，教師可以讓學生參與到精心設計的實驗探究活動中.學生以問題為載體，在教師的引導下進行組內探究學習，體驗探究學習的樂趣，同時培養分析、解決、轉化問題的能力.

例如，在探究“三角形解的個數”時，對如下問題進行變形轉換：

問題：在△ABC中，已知A=30°，a=1，b=2，求B;

變式1：在△ABC中，已知A=30°，a=12，b=2，求B;

變式2：在△ABC中，已知A=30°，a=3，b=2，求B;

變式3：在△ABC中，已知A=30°，a=32，b=2，求B;

變式4：在△ABC中，已知A=120°，a=3，b=2，求B;

變式5：在△ABC中，已知A=120°，a=1，b=2，求B.

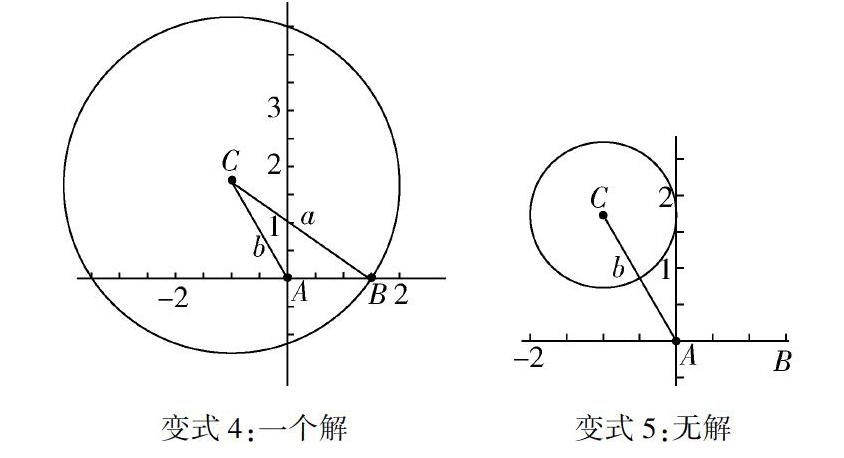
探究：在三角形中，若兩邊和其中一邊的對角已知，那么在怎樣的情況下，求另一邊對角時會出現兩解的情況？一解、 無解呢？學生分組探究，合作交流，教師利用“幾何畫板”進行探究和驗證（如下圖）.

問題：一個解變式1：無解

變式2：一個解變式3：兩個解

變式4：一個解變式5：無解

在探究階段，教師借助“幾何畫板”的動畫模擬功能，可以簡潔而直觀地揭示出三角形解的情況，在此基礎上引導學生進行探究性問題的研究設計.此時，對于學生來說，數學學習變成了一種數學實驗，大大提高了其學習積極性和解決實際問題的能力.

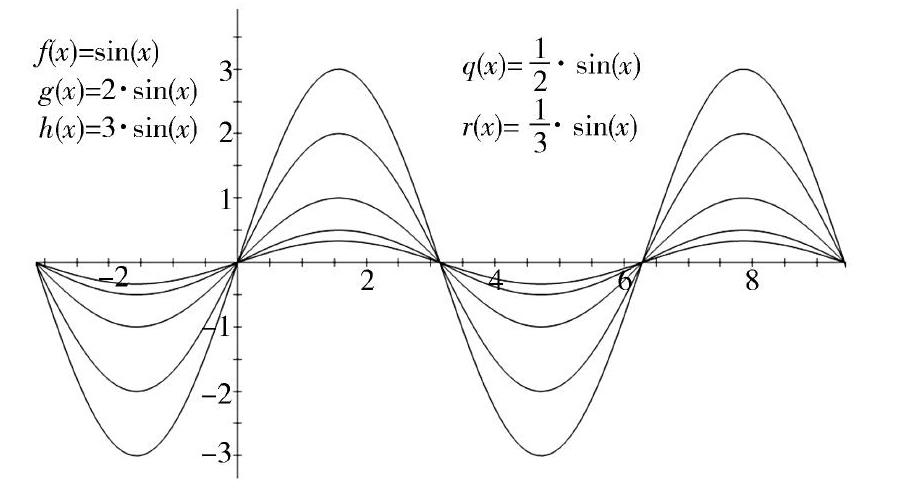
在研究三角函數y=Asin（ωx+φ）的圖像時，教師可以組織學生進行自主探究.學校要為學生創造進入電腦教室學習的機會，同時給學生電腦安裝“幾何畫板”軟件.學生可以分組進行探究，各小組探究y=Asin（ωx+φ）的參數A，ω，φ的變化對函數圖像的形狀和位置的影響.如在“幾何畫板”中畫出y=sin x，y=2sin x，y=3sin x，y=12sin x，y=13sin x的圖像（如下圖），合作探究參數A的變化對函數圖像有什么影響.

學生以“幾何畫板”為平臺進行演示、探究，合作、交流，并歸納總結，最終得出結論.這樣的教學不但直觀、靈活地揭示了知識之間的內在聯系，也為學生提供了動手機會，可以讓學生在實踐中習得真正的知識.

總而言之，“幾何畫板”在高中數學教學課堂上可以發揮輔助工具的作用，教師利用“幾何畫板”進行教學能夠將現代信息技術與數學學科相互融合，為學生創設自由的學習環境，幫助學生更好地學習知識、提高自身能力.

【參考文獻】

[1]陶維林.幾何畫板實用范例教程[M].北京：清華大學出版社，2013.

[2]謝尚鴿.幾何畫板有效融入高中數學課堂教學的研究與實踐[J].中國校外教育，2010（06）：83-84.

[3]劉虹.幾何畫板在高中數學教學中的應用[J].中國現代教育裝備，2010（08）：54-57.