基于灰色關聯度與TOPSIS法的養老機構評價模型分析
——以合肥市為例

李國昌，劉珊珊

(安徽建筑大學 經濟與管理學院，合肥 230000)

一、引言

在黨的十九大報告中，習近平總書記針對人口老齡化問題提出：要積極應對人口老齡化，構建養老、孝老、敬老政策體系和社會環境[1]。尊老愛幼是中華民族的傳統美德，目前我國60歲以上的老年人多是出生于新中國成立之前，經受過戰爭與苦難，對我國的發展與建設都做出過很大的貢獻，而今他們行動不便，自理能力不足，需要社會的支持與照料。切實保障老年人的生活質量既是保障人權的體現，也是時代所賦予的使命[2]。

對于老年人而言，養老生活質量尤為重要。養老機構可以提高老年人的生活便利程度，滿足老年人的多方面需求，從而全方位提升老年人的幸福感[3]。養老機構評價模型可以幫助老年人選擇合適的養老機構，使老年人達到“老有所養、老有所醫、老有所為、老有所安”的理想狀態[4]。

本文在分析眾多養老機構影響因素的基礎上，歸納總結出護理制度、環境出行、硬件設施、服務項目及運行模式5個指標，以此構建養老機構評價指標體系，結果如圖1所示，指標說明如表1所示。

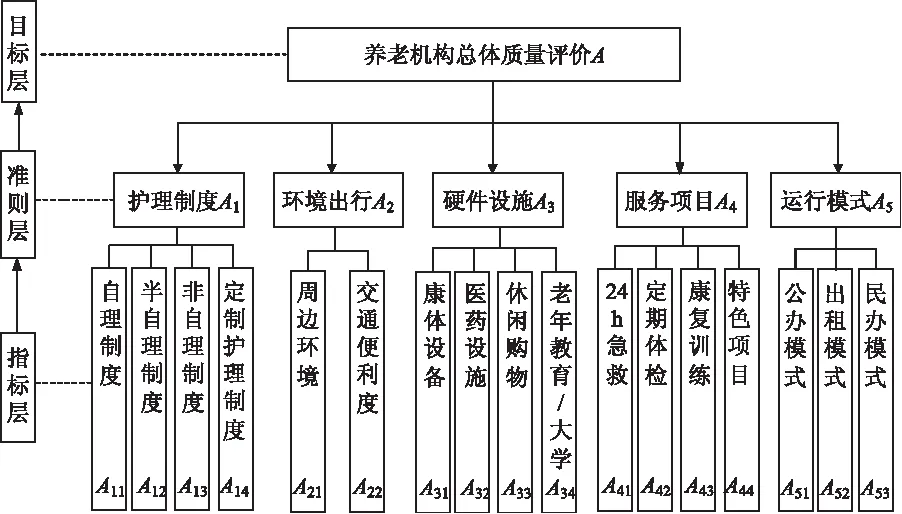
圖1 養老機構評價體系

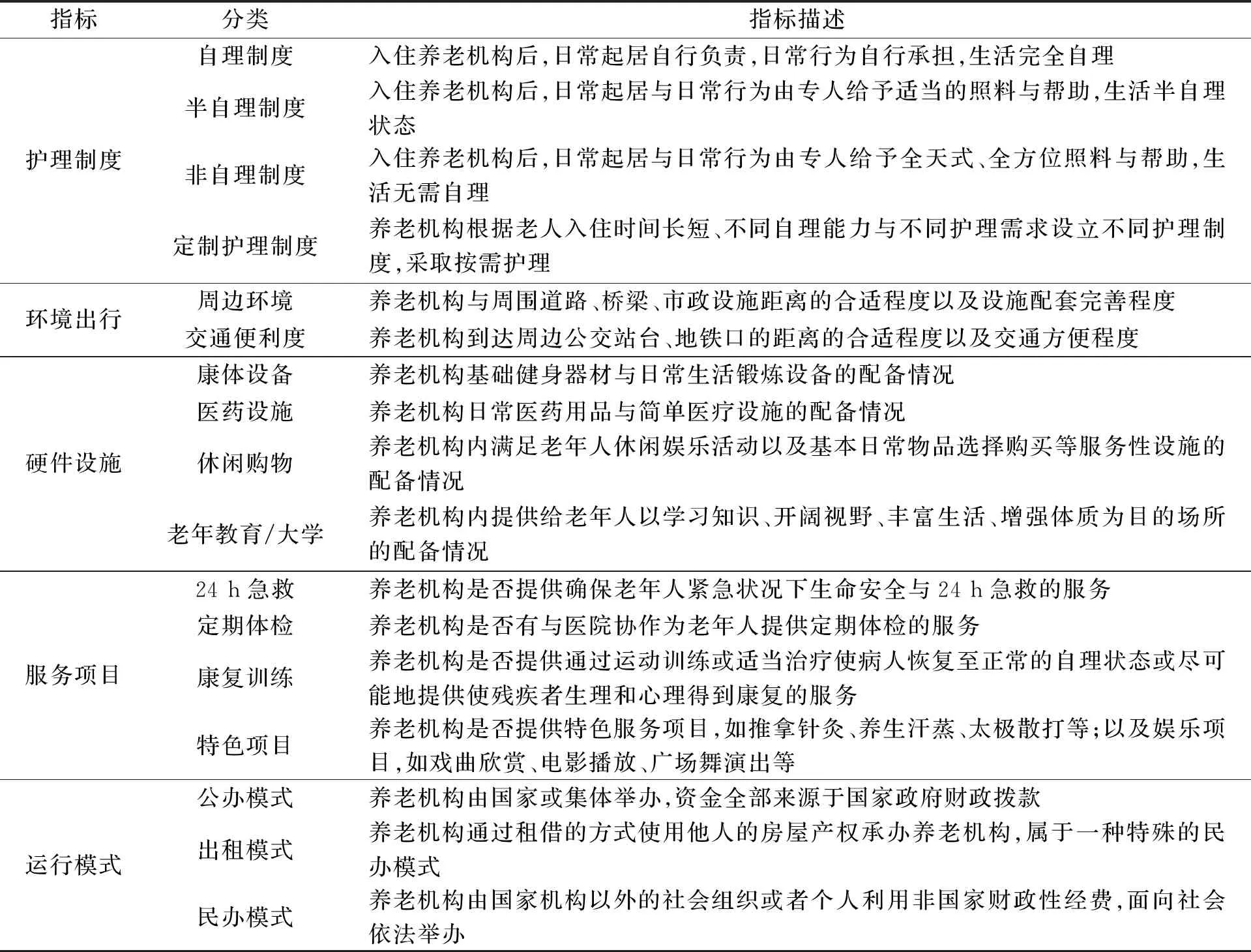
表1 養老機構評價指標說明

二、基于灰色關聯度與TOPSIS法的養老機構評價模型的構建

(一)灰色關聯度與TOPSIS法評價的基本步驟

第一，在對養老機構評價模型中的評價指標進行集合定義的基礎上，利用熵值法構建矩陣，確定各指標權重；第二，利用TOPSIS法構建加權矩陣，確定評價樣本與正、負理想解之間的歐氏距離；第三，采用灰色關聯度法構建待評價樣本與正、負理想解之間的灰色矩陣，確定灰色關聯度；第四，聯合歐式距離與灰色關聯度進行無量綱化處理，計算各樣本的相對貼近度，根據各樣本相對貼近度進行優劣排序。評價流程如圖2所示。

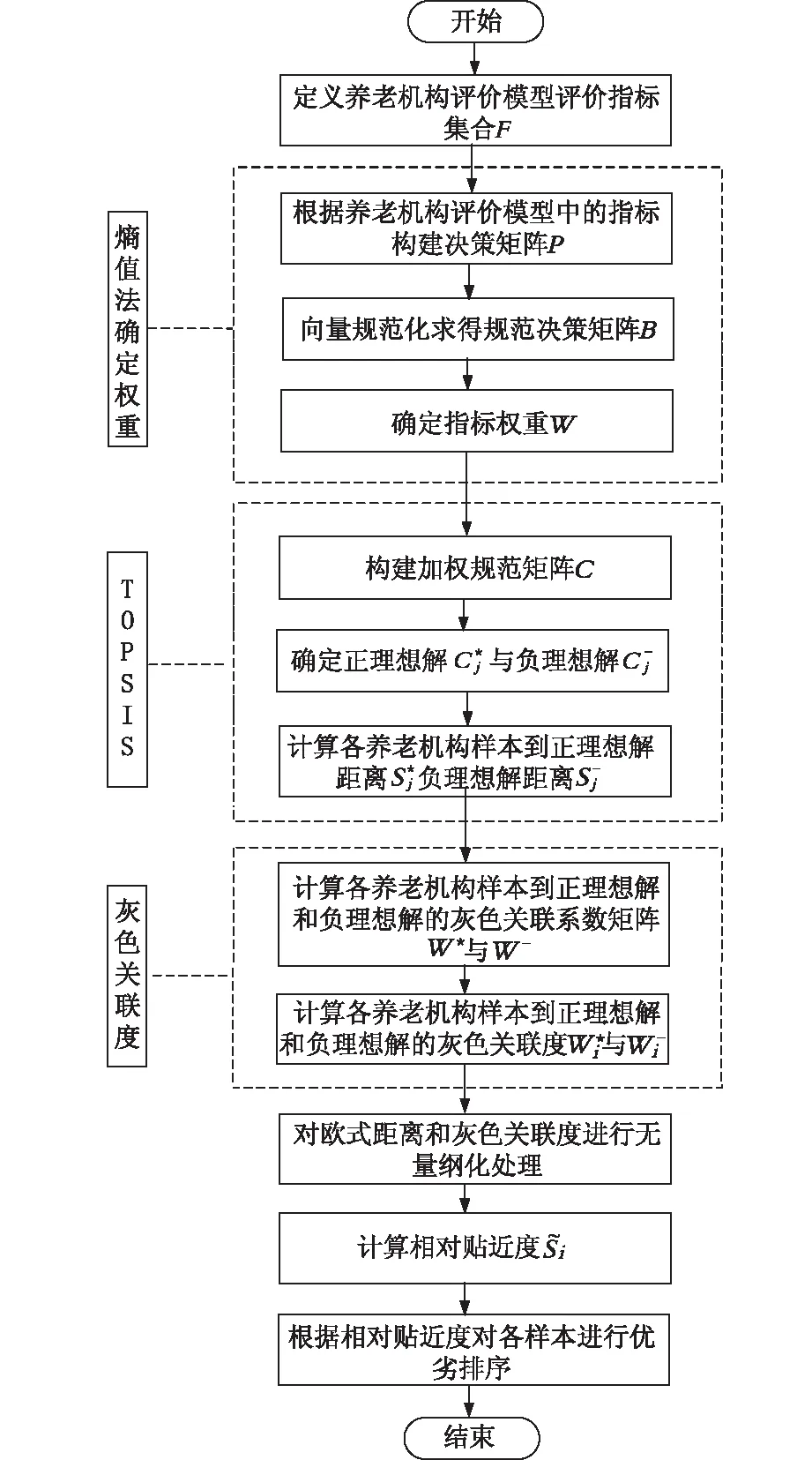
圖2 灰色關聯度與TOPSIS法評價流程圖

(二)評價模型的建立

S1：定義養老機構評價模型評價指標集合F={f1，f2，f3，f4，f5}，該集合共包含5個評價指標：f1為護理制度，f2為環境出行，f3為硬件設施，f4為服務項目，f5為運行模式。

S2：根據養老機構評價模型中各評價指標值構建決策矩陣P。

其中，N為待評價的養老機構的樣本數，xi(f1)為第i個樣本的護理制度，xi(f2)為第i個樣本的環境出行，xi(f3)為第i個樣本的硬件設施，xi(f4)為第i個樣本的服務項目，xi(f5)為第i個樣本的運行模式。

S3：進行向量規范化，求得規范決策矩陣。設規范化決策矩陣B=(bij)N×M，其中

S4：確定指標權重。計算第j項指標下第i個樣本占該指標的比重：

計算第j項指標的熵值：

其中k>0；ln為自然對數；ej≥0；常數k與樣本數M有關，一般令k=1/lnM，則0≤ej≤1。

計算第j項指標的差異系數：gj=1-ej，則gj越大指標越重要。

對于第j項指標，指標值xi(fj)的差異越大，對樣本評價的作用越大，熵值就越小。

求權重：

得到養老機構評價指標的權重向量W=[w1，w2，…，wM]T；

S5：構建加權規范矩陣C=(cij)N×M。

由步驟S4得到養老機構評價指標的權重向量構建加權規范矩陣C，cij=wi×bij(i=1，2，…，N；j=1，2，…，M)。

S7：計算各養老機構樣本到正理想解與負理想解的距離。

S8：計算各養老機構樣本到正理想解和負理想解的灰色關聯度。

計算第i個樣本與正理想解關于第j個指標的灰色關聯系數：

i=1，2，…，N。

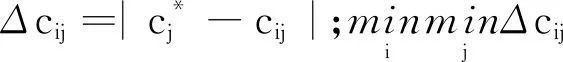
則各樣本與正理想解的灰色關聯系數矩陣為：

第i個樣本與正理想解的灰色關聯度為：

計算第i個樣本與負理想解關于第j個指標的灰色關聯系數：

i=1，2，…，N。

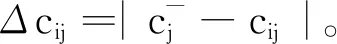
則各樣本與負理想解的灰色關聯系數矩陣為：

第i個樣本與負理想解的灰色關聯度為：

S9：計算相對貼近度。

首先，分別對歐氏距離和灰色關聯度進行無量綱化處理：

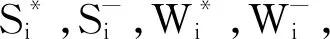
其次，綜合考慮無量綱化后的歐氏距離和灰色關聯度，計算樣本與正理想解和負理想解的接近程度，得到：

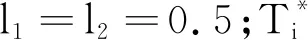
三、養老機構評價模型的應用——以合肥市為例

根據調查資料顯示，截至2018年，合肥市60周歲及以上戶籍人口為1 197 520人，老齡化占比達到合肥市戶籍總人口的16.12%，老齡化程度在全省16個地市中排名第11位。

選取合肥市口碑與經營相對較好的8家養老機構為研究對象，從護理制度、環境出行、硬件設施、服務項目及運行模式5個指標對其進行綜合評價。

數據來源：評價數據采用問卷調查的形式獲得，調查問卷在實際考察當地養老機構的相關情況以及查閱大量相關文獻了解老年人當下養老需求的基礎上進行編制，然后邀請同行專家對問卷的詳細客觀程度評價后審定而成。調查問卷由4部分組成：一是一般資料，包括年齡、性別、受教育程度、婚姻狀況、家庭組成、職業以及月收入等；二是目前的養老現狀，包括老年人的健康狀況、養老機構入住情況等；三是老年人對入住的養老機構各方面的評價，包括養老機構環境出行和硬件設施配備的完善程度以及服務項目的滿意程度等；四是考察老年人對當下養老機構的不滿意之處以及理想的養老機構情況。

問卷調查邀了1 000位養老機構住戶、320位養老機構服務人員以及30位對養老機構有研究的專家填寫問卷。為確保問卷信息真實客觀，養老機構住戶是在家人的幫助下進行問卷填寫的。本次調查共發放調查問卷1 350份，收回1 285份，問卷回收率為95.19%。經過調查組篩選后，剔除無效問卷以及缺失信息較多的問卷，最終獲得有效問卷1 233份，問卷有效率為91.33%。

S1：確定養老機構評價模型評價指標集合。

問卷數據經匯總分析后進行歸一化處理，最終數據如表2所示。

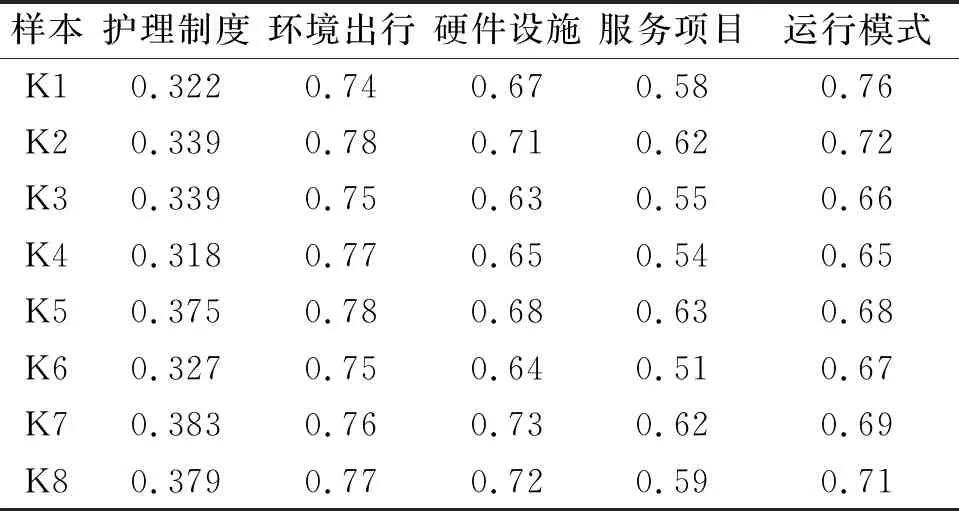
表2 8家養老機構相應數據

S2：構建養老機構評價模型評價決策矩陣P。

S3：通過向量規范化求得規范決策矩陣B。

S4：確定指標權重，計算各機構樣本的評價指標權重向量W。

W=[0.179，0.206，0.206，0.200，0.209]T；

S5：構建加權規范矩陣C=(cij)N×M。

S7：計算各養老機構樣本到正理想解與負理想解的距離，如表3所示。

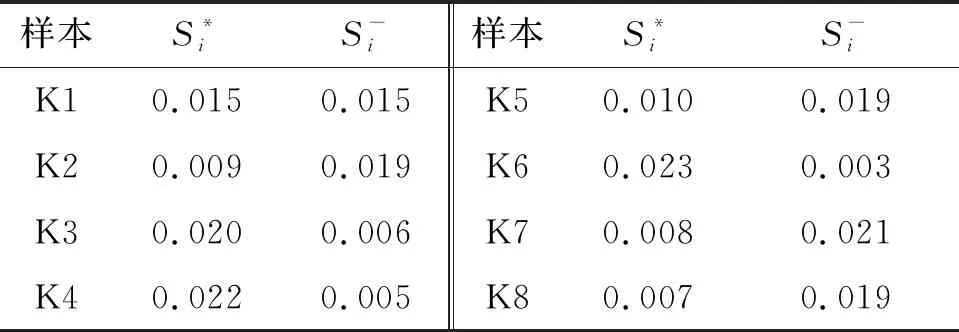
表3 養老機構樣本到正理想解與負理想解的距離

S8：計算各養老機構樣本到正理想解與負理想解的灰色關聯度。

各樣本與正理想解的灰色關聯系數矩陣為：

各樣本與負理想解的灰色關聯系數矩陣為：

各樣本與正、負理想解的灰色關聯度如表4所示。

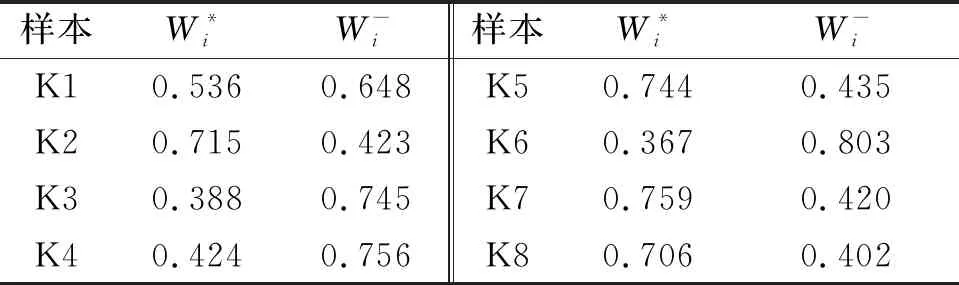
表4 養老機構樣本與正、負理想解的灰色關聯度

S9：計算相對貼近度。

分別對歐氏距離和灰色關聯度進行無量綱化處理，結果如表5所示。

各養老機構樣本到正理想解和負理想解的接近程度如表6所示，相對貼近度如表7所示。

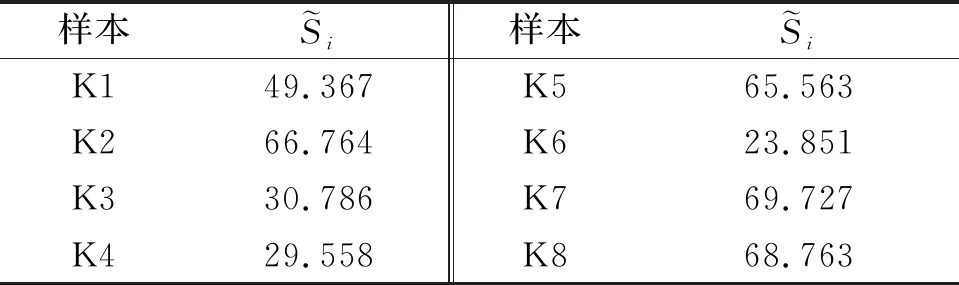
表7 相對貼近度

四、方法對比分析

為了驗證TOPSIS和灰色關聯度法綜合應用比單獨應用的優勢，進行下列對比分析，結果如表8所示。

表8 單獨使用TOPSIS法和灰色關聯度法計算的

從表8中可以看出，在單獨使用TOPSIS方法時，樣本K2優于樣本K5；單獨使用灰色關聯度方法時，樣本K5優于樣本K2，此時無法給決策者一個明確的結論。出現這種情況的原因在于TOPSIS法是基于計算各目標值與理想值之間的歐氏距離來對各個樣本進行優劣排序，假設兩樣本的歐式距離相近，則不能對樣本進行排序。表8中樣本K2與樣本K5的貼近度相近，所以評價結果十分接近，單獨使用TOPSIS法會導致結果失準。而灰色關聯度法只是單純地通過各樣本相同評價指標之間的關聯性來比較各個樣本對統一參考數列的關聯程度，且灰色關聯度法只適用一些基本數據已知的定量指標來進行樣本比選，對于一些無法用具體數據來表示的定性指標，灰色關聯度評價結果是不全面的。本文所選用的指標數據，是通過調查問卷打分獲得的，實際上無法用具體數據來定量表示，所以單純使用灰色關聯度法評價結果也是不準確的。

綜上，單獨使用TOPSIS法或單獨使用灰色關聯度法都無法進行準確評價，而結合灰色關聯度和TOPSIS法獲得的結果可靠性明顯改善，樣本K2與樣本K5差距增大，評價結果更為準確可信。

五、結論

根據相關資料歸納總結出護理制度、環境出行、硬件設施、服務項目與運行模式5個指標，構建了養老機構評價體系，并基于灰色關聯度與TOPSIS法構建了養老機構評價模型。以安徽省合肥市8家經營相近與口碑較好的養老機構為研究對象，通過問卷調查的形式進行數據收集，應用此模型對8家養老機構進行綜合評價。結果表明，樣本K7模式較優，樣本K6模式較差，從指標上看，樣本K7的服務項目與硬件設施水平較高，環境出行與運行模式水平一般，而樣本K6的各指標水平均處于一般狀態。另外，通過對比分析，該模型可以避免單獨使用TOPSIS法進行評價時由于歐式距離相近導致評價結果失準的情況，也可以避免單獨使用灰色關聯度法進行評價時定性指標導致評價結果不全面的情況，將兩種算法進行結合對樣本進行優劣排序，可以確定最佳方案，提高了評價結果的客觀性。