基于改進國密算法與區塊鏈的數據登記系統

鄧建球,方 軼,叢林虎,李海君

(1.海軍航空大學， 山東 煙臺 264001； 2.中國人民解放軍91115部隊， 浙江 舟山 316000)

區塊鏈技術是一種集網絡通信、加密算法、共識機制、智能合約等技術于一體的新興信息技術，具有去中心化、防篡改、可追溯等特點[1]。在區塊鏈技術隨著比特幣出現之后，尤其是近幾年來區塊鏈研究熱度持續增高，各種區塊鏈產業項目層出不窮，許多專家學者已經對區塊鏈在醫療[2]、能源[3]、個人檔案信息[4]、身份認證[5]、物聯網[6]、大數據[7]、云計算[8]等方面的創新與應用進行了較為成功的研究。在區塊鏈技術中采用的Hash函數[9]、Merkle根結構、數字簽名技術[10]、非對稱加密等，是保證區塊鏈數據結構以及數據安全的主要方法手段。

本文首先對區塊鏈以及其中使用的Hash函數與數字簽名技術進行了概述。然后在對兩種國密算法SM2與SM3算法進行原理描述的基礎上，對其進行改進和對比分析。最后，使用區塊鏈Hyperledger Fabric開發平臺針對部隊導彈數據存儲記錄場景進行了應用開發，證明了本文提出的改進國密算法在區塊鏈應用的可行性與有效性。

1 區塊鏈及相關技術

2008年，中本聰發表了一篇名為《Bitcoin:A Peer-to-Peer Electronic Cash System》的論文[11]，提出了一種基于密碼學的電子貨幣，并命名為比特幣(Bitcoin)。而支撐比特幣的這一技術被稱為區塊鏈。區塊鏈具有去中心化、數據防篡改、可追溯等特點[12]，使其非常適用于需要保證數據高可信度以及透明度的場景。區塊鏈技術中使用的Hash函數、非對稱加密、數字簽名技術、共識算法等密碼學算法以及加密技術是保證其數據安全性與可靠性的主要依據。典型的區塊鏈結構如圖1所示。

圖1 區塊鏈結構示意圖

2 SM2算法的改進及其對比分析

SM2算法是我國自主開發的基于橢圓曲線的數字簽名算法。SM2算法主要包括系統參數生成(包括橢圓曲線參數生成和用戶公私鑰生成)、數字簽名生成和數字簽名認證三部分[13]。

2.1 SM2算法

系統參數主要包括有限域Fq的規模及表示，定義橢圓曲線E(Fq)方程的兩個元素a,b∈Fq；E(Fq)上的基點G=(xG,yG)(G≠0)；G的階n等。

假設簽名用戶為A，則還需要生成簽名用戶A的私鑰dA和公鑰PA=[dA]G=(xA,yA)；長度為entlenA比特的可辨別標識IDA，由entlenA轉換成的兩字節ENTLA；將其他參數轉換成比特串形式。

最后對以上參數使用SM3算法進行Hash運算，得到256位的與以上系統參數向關聯的比特串ZA=HashSM3(ENTLA‖IDA‖a‖b‖xG‖yG‖xA‖yA)。

假設待簽名的消息為M，簽名用戶A通過以下步驟獲得對消息M的簽名(r,s)：

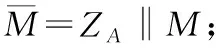
A3：用隨機數發生器產生隨機數k∈[1,n-1]；

A4：計算橢圓曲線點(x1,y1)=kG，將x1化為整數；

A5：計算r=(e+x1)modn，若r=0或者r+k=n，則返回A3；

A6：計算s=(1+dA)-1·(k-r·dA)modn，若s=0，則返回A3；

A7：將r、s轉化為字節串，得到M的簽名(r,s)。

假設用戶B收到了待驗證的消息M′及其數字簽名(r′,s′)，通過以下步驟對簽名進行認證：

B1：驗證r′∈[1,n-1]是否成立，若不成立則驗證失敗；

B2：驗證s′∈[1,n-1]是否成立，若不成立則驗證失敗；

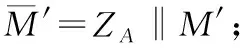
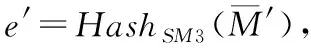
B5：將r′、s′化為整數，計算t=(r′+s′)modn。若t=0則驗證失敗；

2.2 改進的SM2算法

改進策略主要通過對SM2簽名算法中的求逆運算進行改進，在保證簽名及認證結果正確性的基礎上，通過變量的代換使整個過程不含有求逆運算，從而提高SM2數字簽名算法的執行效率。本文提出的改進SM2數字簽名算法執行過程如下(與原算法相同的步驟不再重復)：

在數字簽名生成中，A1至A5步驟同原SM2算法的步驟A1至A5，對簽名公式A6進行改進：A6：計算s=k-r+dAmodn，若s=0，則返回A3；A7同原SM2算法的步驟A7。

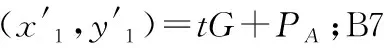
根據本文的改進方案，若用戶A對消息M進行了有效簽名，簽名s′=k-r′+dAmodn，變形整理可得k≡s′+r′+dAmodn，從而kG≡(s′+r′+dA)G成立，則kG≡s′G+r′G+dAG≡(s′+r′)G+PA≡tG+PA成立。因此驗證結果正確與否取決于R=r′是否成立。證明該方案與原方案具有相同的簽名及認證效果。

2.3 運算復雜度分析

使用Go語言對SM2算法進行實現，并使用Go語言內置的pprof性能分析工具，對壓力測試進行性能分析，得到SM2算法中各種運算及函數的運算耗時占比，如表1所示。

表1 SM2算法運行耗時占比

在SM2算法中，主要進行了Hash函數運算、模逆運算、點乘運算和橢圓點計算，將本文提出的改進SM2算法與原始SM2算法中的各種運算進行對比，具體情況如表2所示。

表2 運算復雜度對比

從表2中可以看出，改進后的SM2算法不含有模逆運算，并且減少了2次點乘運算。從表1中也可以得知，模逆運算是耗時占比最多，復雜度最高的運算，因此，降低模逆運算的次數，使改進SM2算法運算復雜度低于原SM2算法。

3 SM3算法的改進及對比分析

3.1 SM3算法

SM3算法是我國提出的一種迭代Hash算法，其輸入和輸出都是比特串。SM3算法的輸出長度為256比特，消息分組為512比特，采用MD結構。對于長度小于264比特的消息X，SM3算法經過填充和迭代壓縮，生成雜湊值，雜湊值長度為256比特。具體算法描述如下[14]。

SM3算法中定義了布爾函數FFj(X,Y,Z)、GGj(X,Y,Z)和置換函數P0(X,Y,Z)、P1(X,Y,Z)，具體定義如下。

P0(X)=X⊕(X<<<9)⊕(X<<<17)

P1(X)=X⊕(X<<<15)⊕(X<<<23)

上述式子中的X、Y、Z均為長度為32的比特串。

對于一個長度為l比特的消息，首先將比特“1”添加到消息的末尾，再添加k個“0”，其中k是滿足l+1+k≡448 mod 512的最小非負整數，然后添加一個64位的長度l二進制比特串。經過這樣填充后的消息的長度就是512的倍數。

將填充后的消息按每512比特的長度為一組進行分組，并對分組后的消息進行編號，得到B(0)B(1)…B(n-1)，其中n=(l+k+65)÷512。對分組后的已填充消息進行如下方式的迭代：

FORi=0 TOn-1

V(i+1)=CF(V(i),B(i))

END FOR

其中，CF是壓縮函數，V(0)是初始值IV，長度為256比特。最后一次迭代后的結果為V(n)。

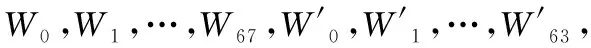
FORj=16 TO 67

Wj←P1(Wj-16⊕Wj-9⊕(Wj-3<<<15))⊕

(Wj-13<<<7)⊕Wj-6

END FOR

FORj=0TO63

END FOR

壓縮函數的計算過程如下：

ABCDEFGH←V(i)

FORj=0 TO 63

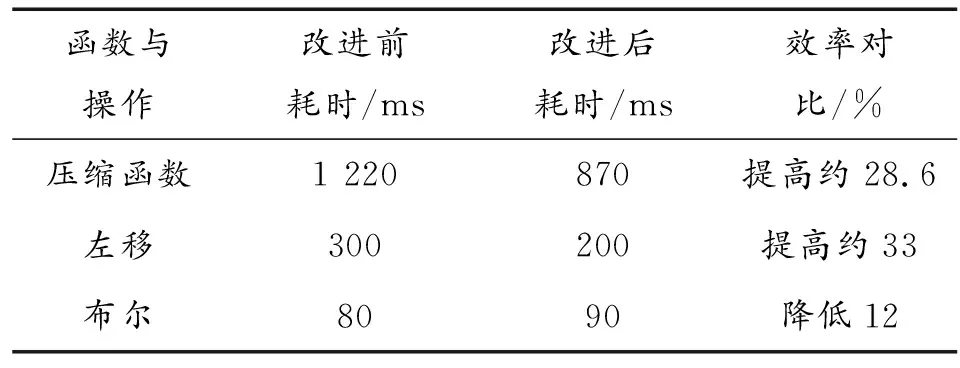
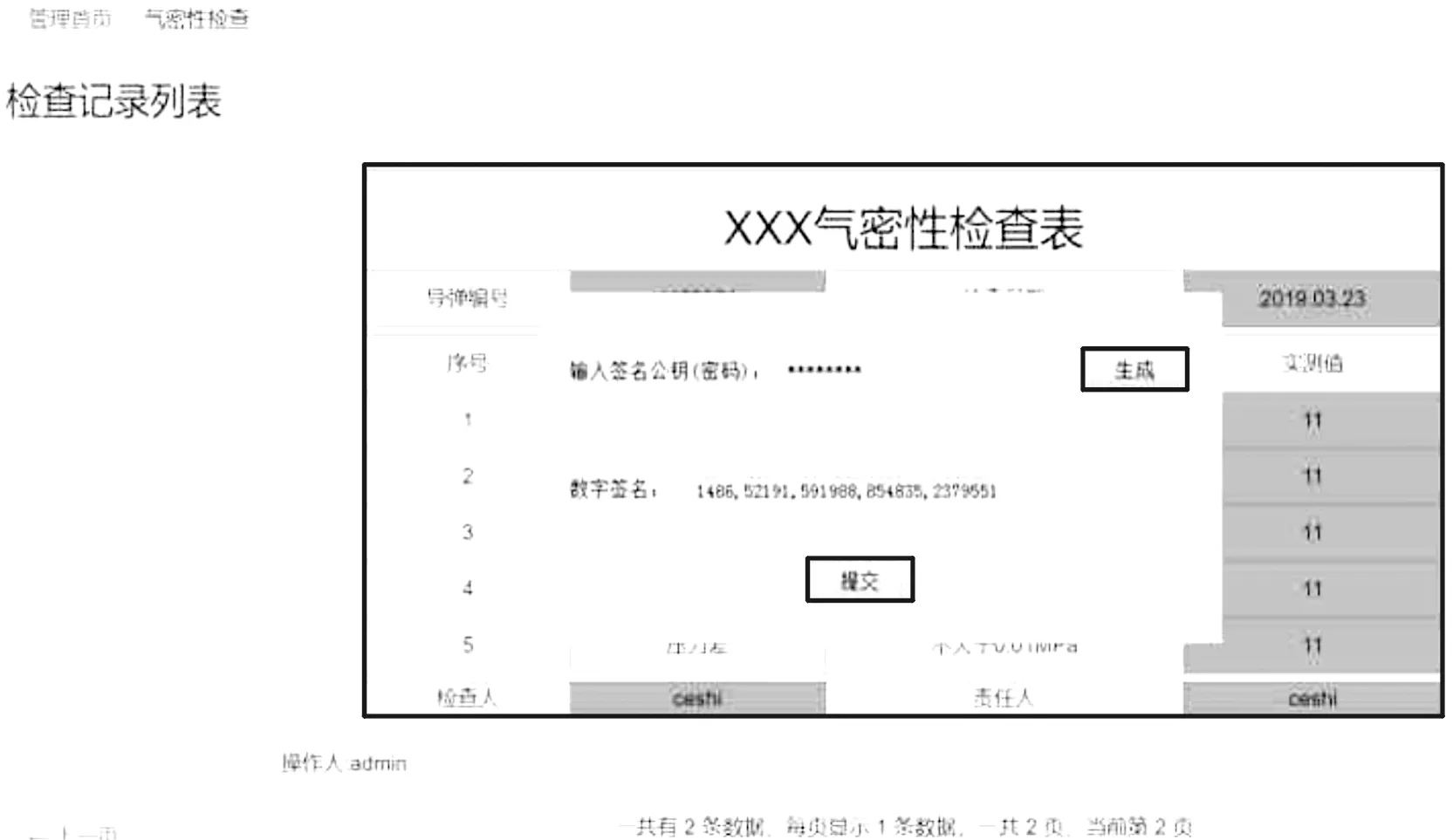
SS1←((A<<<12)+E+(Tj<<

SS2←SS1⊕(A<<<12)

TT2←GGj(E,F,G)+H+SS1+Wj

D←C

C←B<<<9

B←A

A←TT1

H←G

G←F<<<19

F←E

E←P0(TT2)

END FOR

V(i+1)←ABCDEFGH⊕V(i)

其中，A,B,C,D,E,F,G,H是中間變量,SS1,SS2,TT1,TT2是字寄存器。且字的存儲方式為大端存儲。最后輸出的256比特雜湊值為y=ABCDEFGH。

3.2 改進的SM3算法

SM3算法中，壓縮函數主要過程是中間變量的賦值、移位運算以及寄存器中數據的讀寫，且使用了多個中間變量與多個寄存器，讀寫寄存器中的數據占用了大量的運算時間。因此可以通過優化中間變量、減少對寄存器中的數據讀寫次數的方式來達到降低壓縮函數運算時間的目的，使用此方法進行改進的同時也不會破壞原有壓縮函數結構，保證了結果仍然可靠，同時在對消息進行擴展時也可以進行一些優化改進。具體改進策略如下：

首先將消息分組B(i)劃分為16個字：W0,W1,…,W15。并將前4個字存儲在中間變量W0,W1,W2,W3中，用于壓縮函數的第一次計算。壓縮函數中的SS1,SS2,TT1,TT2都是中間變量，因此需要減少這些中間變量的使用。優化方案主要集中在壓縮函數循環體的前四步操作中，剩余相同部分不再給出。同時結合消息擴展部分的優化方案，在前文SM3算法描述的基礎上，壓縮函數進行優化改進后的描述如下：

ABCDEFGH←V(i)

FORj=0 TO 63

TT1←FFj(A,B,C)+D+((((A<<<12)+E+

(Tj<<

ifj>16

TT2←GGj(E,F,G)+H+(((A<<<12)+E+

(Tj<<

(Wj-3<<<15))⊕(Wj-13<<<7)⊕Wj-6

else

TT2←GGj(E,F,G)+H+(((A<<<12)+E+

(Tj<<

D←C

C←B<<<9

……

使用Go語言內置的pprof性能分析工具，對壓力測試進行性能分析。測試結束后使用top命令可以得到前十個運算耗時以及占用資源最多的函數，將結果整理成表格，如表3所示。

表3 改進SM3算法效果對比

與原始SM3算法運行情況對比，總用時減少了約25%，其中壓縮函數效率明顯提高，提高了約30%，證明優化改進方案能夠有效提高SM3算法的運行效率。

4 改進國密算法在區塊鏈中的應用

本文在改進SM2算法的基礎上使用Hyperledger Fabirc平臺，針對導彈業務數據存儲場景進行區塊鏈應用開發。使用Fabric平臺進行開發時，在其加密組件BCCSP中對使用的改進算法進行實現，本文采用Go語言對改進SM2和SM3算法進行實現。

在邏輯層開發上，Fabric中使用到了智能合約機制。智能合約是一段運行于沙盒環境下的代碼，可以保證系統的運行邏輯不被篡改。開發Fabric區塊鏈應用時,最重要的就是進行智能合約的編寫。編寫的系統智能合約中的函數如表4所示。

表4 系統智能合約中的部分函數

圖2是該系統完成數據錄入后進行數字簽名界面。

圖2 系統界面

5 結論

針對重要數據的記錄與存儲以及區塊鏈應用中加密算法國產化問題，對SM2數字簽名算法與SM3密碼雜湊算法進行了改進，降低了SM2算法的運算復雜度，將SM3算法運行效率提高約25%；采用本文的改進方案使用Hyperledger Fabric開發平臺針對部隊導彈數據存儲、記錄場景，開發了基于區塊鏈的導彈數據管理系統，證明了方案的可行性，為區塊鏈技術在部隊中的應用提供了理論與實踐基礎。