兩級串聯型ISD懸掛構型設計與分析

徐 龍，毛 明，陳軼杰，杜 甫

(中國北方車輛研究所， 北京 100072)

車輛行駛時的振動主要通過懸掛系統抑制[1]。傳統懸掛系統結構單一，限制了懸掛系統的隔振性能。直到慣容器的概念被Smith等人提出[2]，傳統被動懸掛系統才得到了飛躍式的發展。近年來，車輛懸掛構型由于慣容器的引入變得多種多樣，針對懸掛構型設計的研究也層出不窮。

2012年，陳龍等[3]利用電路網絡中的級聯濾波思想，根據機電相似關系設計了一種兩級串聯式ISD懸掛構型；2014年，杜甫[4]對包含一個慣容器的ISD懸掛構型進行拓撲結構設計，得出了一種通用構型；2017年，Sara Ying Zhang[5]提出了一種子構型串并聯形成新構型的設計方法，構建了許多新懸掛構型。上述設計方法中，都設計了兩級串聯型ISD懸掛構型。而且通過試驗分析，均驗證了兩級串聯式構型具備優良的隔振性能。但是未曾發現有學者對所有兩級串聯型ISD懸掛進行系統研究，本文旨在提出兩級串聯型ISD懸掛通用網絡，對比分析不同形式的兩級串聯型ISD懸掛的隔振性能。

文中提出了一種6元件兩級串聯式ISD懸掛隔振網絡，利用疊加法結合電路中的拓撲設計方法(支路對應元件，結點對應節點[6])，構建了4種工程上可實現的兩級串聯式ISD懸掛構型，并利用機械阻抗原理構建頻域內的通用阻抗動力學模型。同時，對第二級元件參數進行優化，由簡到繁逐步對4種懸掛構型進行分析，對比4類懸掛的幅頻特性，選出性能較優的兩級串聯式ISD懸掛構型。

1 ISD兩級隔振拓撲網絡建立

文獻[5]中描述了一種復雜隔振網絡的設計方法：首先通過分析法找到子構型，然后將子構型進行串并聯分析，最終得到隔振網絡通用構型。上述方法約束慣容數量≤阻尼數量≤彈簧數量，在對包含多個慣容器的隔振網絡設計時，彈簧和阻尼數量過多，增加了元件數量，從而提高了隔振網絡的復雜度。鑒于此，本文取消對元件數量的約束，將三元件并聯ISD隔振構型作為子構型，對該子構型進行串并聯疊加形成新構型。結合圖論的支路結點圖，繪制出隔振拓撲網絡，并對應出隔振網絡構型。同時，根據疊加分析法的原理，以及各元件的基本特點，給定如下設計約束：

1) 由于設計時以三元件并聯ISD隔振構型作為基礎構型，因此設計的網絡中應至少包含一個完整子構型；

2) 根據彈簧、阻尼和慣容同類元件并聯等效的特點，約束并聯的支路數量不超過3；

3) 由于阻尼、慣容不能單獨承受靜載荷，因此串聯型隔振構型的每一級必須存在彈簧元件用以承載；

根據上述約束條件得到表1 S2～S5所示的4種兩級串聯拓撲網絡以及相對應的應用于車輛懸掛系統的隔振構型。

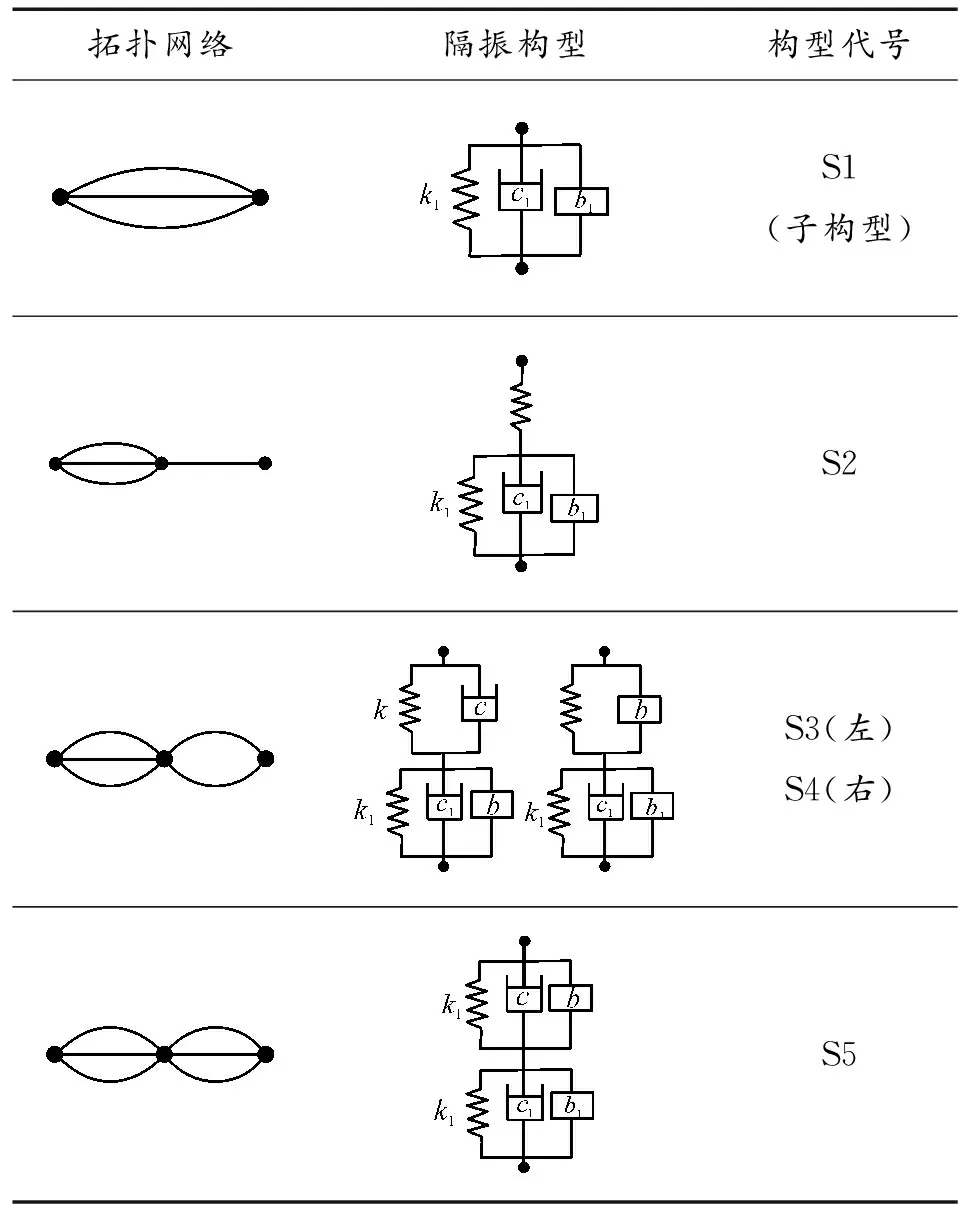
表1 子構型及其衍生兩級ISD構型

由表1可以看出，S5在某個慣容或阻尼元件失效時等效于其他3種構型，因此可以作為表中構型S2～S5的通用模型，即兩級串聯式隔振網絡通用構型。

2 機械阻抗

電路系統中，電容、電阻以及電感在構成電路時，可以通過電路網絡的阻抗特性來描述其電學特性。在機械系統中，根據機電相似理論提出了機械阻抗及其倒數——機械導納的概念，用以表達機械網絡的力學特性[7]。

其中，機械阻抗定義為線性定常穩定系統的簡諧激勵與其引起的穩態響應的復數比或幅值之比。設系統的激勵力為f(t)，穩態響應為x(t)，則系統的機械阻抗Z(s)和機械導納H(s)分別為

(1)

(2)

式中：e為自然對數函數的底數；s為拉普拉斯變換的復變量，s=σ+jω；

將s=jω代入式(1)(2)中，得

(3)

(4)

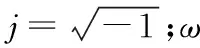
從式(3)、式(4)可以看出，系統的機械阻抗是激勵力f(t)與穩態響應為x(t)的傅里葉變換之比，機械導納是其倒數。

懸掛系統是經典的機械隔振網絡，根據新機電相似理論，新型懸掛系統可以包括彈簧、阻尼以及慣容三類元件。在懸掛系統中，其輸出的響應量可以是位移、速度以及加速度，與之對應的機械阻抗也存在3種不同的形式：位移阻抗、速度阻抗以及加速度阻抗(見表2)。

表2 三類機械元件的機械阻抗

文獻[8]中詳細分析了各機械元件串聯和并聯時的阻抗特性，并得出了以下結論：

1) 對于任意個機械元件組成的串聯系統，系統的速度阻抗的倒數等于各元件阻抗倒數的代數和，即：

(5)

2) 對于任意個機械元件組成的并聯系統，系統的速度阻抗為各元件速度阻抗的代數和，即：

(6)

根據位移阻抗、速度阻抗和加速度阻抗之間的代換關系，可知以上結論推廣到位移阻抗和加速度阻抗同樣適用。

3 ISD懸掛動力學模型建立

以S5所示結構作為懸掛結構，并建立二自由度單輪懸掛動力學模型，如圖1所示[9]。圖中懸下質量和懸上質量分別用m1和m2表示，車輪剛度用kt表示，k、k1、c、c1、b、b1分別是懸掛剛度、阻尼和慣容器慣質系數，z1、z、z2分別為懸下質量m1、網絡中間節點以及懸上質量m2在路面激勵q作用下的垂直方向上的位移。由以上條件根據牛頓第二定律可以列出該車輪雙質量系統的動力學方程：

(7)

由于兩級串聯型懸掛兩級中間存在浮動節點，式(7)多了一個中間式，增加了計算復雜度。由上述機械元件的串并聯阻抗特性，可以將上述二自由度動力學模型簡化為圖2所示的二自由度阻抗動力學模型[10]。

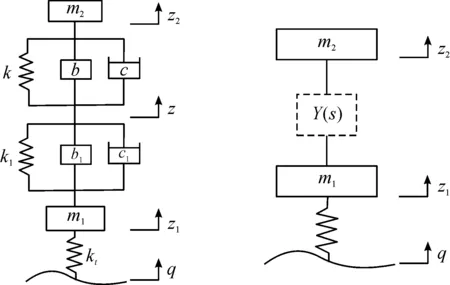
圖1 ISD懸掛雙質量二自由度動力學模型 圖2 ISD懸掛雙質量二自由度阻抗動力學模型

圖2中，Y(s)表示S5的機械阻抗：

(8)

根據式(8)，圖2所示模型的拉普拉斯變換動力學方程為：

(9)

整理式(9)得：

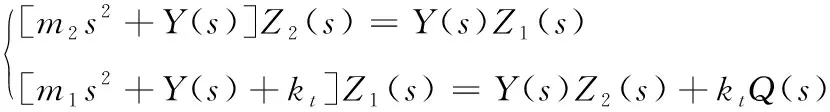
(10)

式中，s為復變量，由式求得z2/z1的傳遞函數G1(s)：

(11)

將式(11)代入式(10)得z1/q的傳遞函數G2(s)：

(12)

式(11)與式(12)相乘得z2/q的傳遞函數G3(s)：

(13)

4 懸掛參數優化

4.1 懸掛性能評價指標

在單輪懸掛系統分析時，通常用懸上質量加速度(ACC)來表征乘員乘坐舒適性；利用車輪動載荷(DLT)表征車輪的行駛安全性和操縱穩定性；利用懸掛動行程(SWS)對車輪上下位移的行程進行約束限制。因此上述3個指標常用來評價懸掛系統的性能。

懸上質量加速度，即m2的垂直方向的加速度

(14)

車輪動載荷，即車輪與地面之間的動態載荷

DLT=kt(z1-q)

(15)

懸掛動行程，即車輪相對于車體在垂直方向上的位移

SWS=z2-z1

(16)

根據式(11)～式(13)，可以求得ACC、DLT以及SWS在路面激勵q下的幅頻特性，根據幅頻特性曲線可以分析出各元件參數對懸掛系統特性的影響，并對參數進行優化設計。

(17)

(18)

(19)

通常，ACC和DLT作為懸掛系統優化的目標函數，SWS作為約束條件，防止車輪動行程過大，頻繁撞擊限位塊。將三元件并聯系統的位移阻抗Y(s)代入到式(17)～(19)中，H1(s)，H2(s)和H3(s)表示的就是三元件并聯ISD懸掛系統3個評價指標的傳遞函數[11]。

4.2 目標函數與約束條件

ISD懸掛的參數優化是一個典型的多目標優化問題。對于其描述見式(20)[12]

(20)

其中：x為優化變量，fi(x)為目標函數，lb和ub分別對應優化變量的上下限，其余的等式和不等式分別為變量x的線性約束和非線性約束。

對于多目標優化問題，通常采用利用權系數將各個目標函數轉化為單一目標進行參數優化，對于ISD懸掛系統的參數優化，目標函數如式(21)[13]。

(21)

由于車輛懸掛系統注重于乘員乘坐舒適性，故將ACC的加權系數取為0.6，將DLT的加權系數取為0.4。同時，又因為ACC與DLT的量綱不同，需要對其進行歸一化，故將各個目標函數除以對應的S1構型的加速度均方根值ACC*和動載荷均方根值DLT*。

為了快速有效的得到最優解，需要對優化參數加以約束，約束條件如下：

1) 正實約束

懸掛參數只有在大于0時才具有工程意義，故優化參數x>0；

2) 偏頻約束

懸掛系統偏頻影響懸掛系統性能，故偏頻需在一定范圍內，即

(22)

式中，k*和b*為懸掛網絡等效剛度和等效慣質系數。

懸掛動行程約束

懸掛工作時動行程不應超過約束值SWS*，即

SWSmax≤SWS*

(23)

5 兩級串聯型ISD懸掛系統性能分析

為了研究第二級不同構型對串聯型ISD懸掛性能的影響，以具體車型參數(表3)對上述5種構型進行性能分析，以三元件并聯ISD懸掛參數作為基礎(即第一級元件參數不變)，逐個分析添加元件后對懸掛系統性能的影響。并與三元件并聯ISD懸掛結構分別從ACC、DLT和SWS等方面進行幅頻特性對比，分析各兩級串聯型ISD懸掛的系統性能。

表3 三元件并聯ISD懸掛性能參數

5.1 路面隨機輸入

(24)

基于式(17)～式(19)中求得的傳遞函數可以求出其對應的功率譜密度函數：

(25)

由于ACC、DLT和SWS在隨機振動響應下幅值取正、負值的概率相等，其均值為0。因此，上述量的方差等于其均方值，根據式(26)求得均方根值[15]：

(26)

5.2 各懸掛振動響應

設車速v1=10 m/s，參考空間頻率n0=0.1 m-1，路面不平度系數Gq(n0)=1 024×10-6m3。在上述輸入條件下對4種串聯型構型進行優化仿真，優化參數如表4所示。幅頻特性如圖3～圖6所示。

表4 各串聯型ISD懸掛構型參數

由圖3可以看出，傳統三元件并聯ISD懸掛與彈簧k串聯形成的串聯型構型S2在低頻和高頻幅值都有較嚴重的惡化情況，雖然在中頻段有較好的的穩態響應，但是高低頻激勵會使懸上質量產生劇烈共振，因此S2不適合作為車輛懸掛結構。

圖4中的S3是傳統三元件并聯ISD懸掛與SD懸掛串聯的構型，即傳統的兩級串聯型ISD懸掛。該懸掛構型在低頻段和高頻段均表現出了較為優良的隔振性能，尤其是對高頻段的懸上質量加速度的抑制效果相對于構型S1有了明顯的改善。由于構型S3減振效果明顯，故適合作為車輛懸掛結構。

圖5所示的S4是S1與慣容-彈簧諧振網絡串聯行程的兩級串聯ISD構型。由于引入并聯諧振網絡，使得該懸掛構型在低頻段出現了反共振現象，但是由于伴隨著反共振峰同時出現的共振峰幅值過大，嚴重影響了懸掛系統低頻段的穩態響應，因此該構型不適合作為車輛懸掛結構。

S5是兩個S1串聯構成的兩級串聯ISD構型。從圖6中可以看出構型S5與S1的功率譜密度函數曲線基本重合，構型S5在低頻段相對于S1在低頻段表現出了比較好的響應特性，其余頻率段兩種構型特性相似。但是由于S5構型復雜，現階段不適合用于車輛懸掛上，若慣容懸掛集成化技術有較大突破，可以考慮將S5應用于車輛懸掛上。

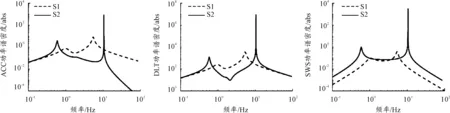
圖3 S2與S1時的功率譜密度

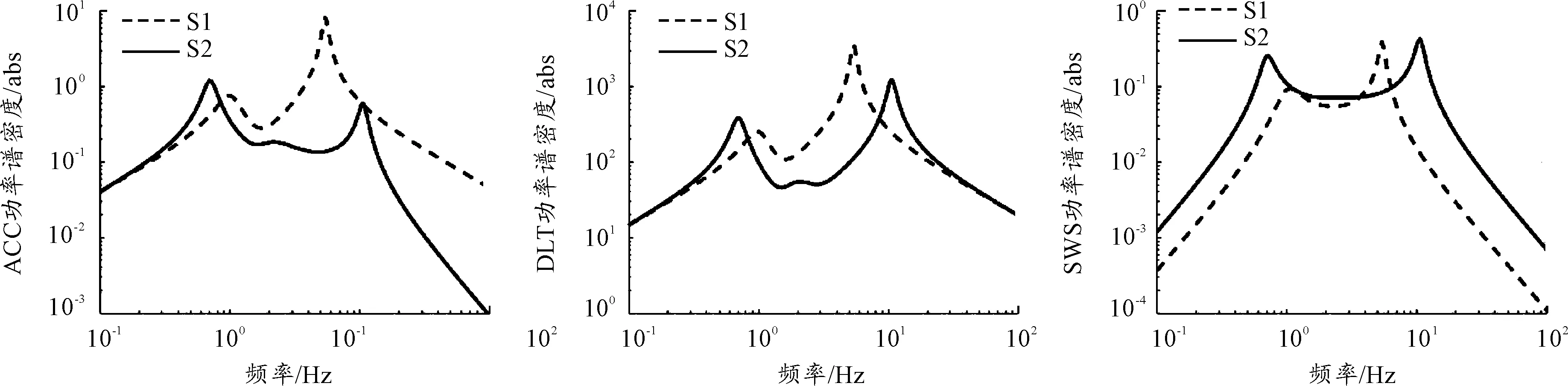
圖4 S3與S1時的功率譜密度

圖5 S4與S1時的功率譜密度

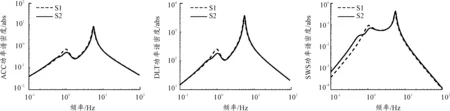
圖6 S5與S1的功率譜密度

6 結論

1) 疊加分析法與拓撲網絡的結合能夠快速有效求得到相對復雜的ISD懸掛構型。

2) 基于疊加分析法與拓撲設計方法建立了6元件兩級串聯型ISD懸掛構型。得到的4種懸掛構型中，S3和S5構型能夠使懸掛系統性能優于傳統三元件并聯ISD懸掛。

3) 機械阻抗動力學建模方法在懸掛網絡構型設計優化時具有普適性。