基于協(xié)方差稀疏迭代的柱面共形陣2-D DOA估計

張狀和,韓 東,劉德亮

(陸軍工程大學(xué)石家莊校區(qū) 導(dǎo)彈工程系，石家莊 050003)

共形陣列天線[1]是一種和事先規(guī)定的物體外形共形，而且又不會帶來額外負(fù)擔(dān)的天線，這些物體例如飛機、導(dǎo)彈、高速列車、衛(wèi)星等，共形陣列天線可以滿足上述物體的空氣動力學(xué)需求，而且還能有效減少荷載的大小和重量；另一方面，在天線集成時，諸如城市等通信環(huán)境中亦較少地被干擾。傳統(tǒng)的波達方向(Dimensional Direction of Arrival,DOA)估計研究，其仿真實驗大多設(shè)置在線陣、平面陣環(huán)境下，因此研究共形陣DOA估計方法具有重要意義。目前，在共形陣高精度、高分辨率DOA估計方面，國內(nèi)外有很多有價值的研究成果。

文獻[2]通過將共形陣分解為較小的子陣列，使用插值技術(shù)，改進了多重信號分類算法(Multiple Signal Classification,MUSIC)，理論上適用于任意形狀的共形陣；文獻[3]使用交叉偶極子建立了四元數(shù)表示的錐面共形陣列模型，通過秩損原理實現(xiàn)了高精度2-DDOA估計；文獻[4]充分利用柱面載體的單曲率特征，應(yīng)用旋轉(zhuǎn)不變參數(shù)估計技術(shù)(estimation of signal parameters via rotational invariance techniques,ESPRIT)，實現(xiàn)了盲極化2-DDOA估計；文獻[5-6]考慮到共形陣載體曲率對方向圖的影響，利用歐拉旋轉(zhuǎn)變換公式，建立了共形天線陣列導(dǎo)向矢量模型。文獻[7]則提出了一種基于張量技術(shù)的共形陣2-DDOA估計，該方法利用共形陣接收數(shù)據(jù)的多維信息構(gòu)建三階張量，通過協(xié)方差張量的高階奇異值分解來獲得期望信號子空間，進而利用子空間類算法實現(xiàn)2-D DOA估計。上述研究均引入了經(jīng)典的子空間類算法來解決共形陣DOA估計問題，但是這類算法在對樣本協(xié)方差矩陣進行特征分解時，往往需要大量的快拍數(shù)據(jù)支撐，以保證信號子空間與噪聲子空間不發(fā)生混疊。但是在實際的工程應(yīng)用中，信號經(jīng)常處于不能長時間穩(wěn)定或快速時變的環(huán)境中，采集大量的快拍數(shù)據(jù)會導(dǎo)致處理時間過長、增大與真實樣本的誤差等問題。相比于子空間類算法，稀疏類算法利用真實頻率的稀疏性，在實現(xiàn)高分辨率的同時，還降低了算法對快拍數(shù)的需求，2010年P(guān)etre Stoica等[8-10]等關(guān)注了信號真實頻率在頻域的稀疏性，提出了基于協(xié)方差稀疏迭代的譜估計方法(sparse iterative covariance-based estimation method,SPICE)。相比于其他稀疏類方法，SPICE計算負(fù)擔(dān)較小，且無需精細地選擇用戶參數(shù),甚至在只有一個快拍數(shù)據(jù)的條件下，也可以達成高精度、高分辨率DOA估計的目的。

柱面共形陣作為最常見的共形陣形式之一，在通信、雷達系統(tǒng)的天線集成設(shè)計等領(lǐng)域有著廣闊的應(yīng)用前景。本文在應(yīng)用歐拉旋轉(zhuǎn)變換建立柱面共形陣的窄帶快拍數(shù)據(jù)模型基礎(chǔ)上，應(yīng)用SPICE方法，將基于統(tǒng)計可靠的加權(quán)數(shù)據(jù)協(xié)方差擬合代價函數(shù)轉(zhuǎn)換為凸優(yōu)化問題，構(gòu)造循環(huán)最小化器，具有全局收斂特性；最后迭代收斂，繪制出每個掃描點的三維能量譜圖，譜峰所對應(yīng)方位角和俯仰角即為信號源2-D DOA的估計值。

1 柱面共形陣列數(shù)據(jù)模型

假設(shè)有K個互不相關(guān)的遠場窄帶信源入射到M×N元柱面共形陣上，陣元數(shù)為D=N×M，其結(jié)構(gòu)如圖1所示。坐標(biāo)原點的位置即為參考陣元位置，定義n為由下至上的圓環(huán)序號，m為每一圓環(huán)上逆時針方向的陣元序號，R表示圓柱半徑，H表示圓柱的高，d為上下兩陣元間的距離；歐拉旋轉(zhuǎn)變換在文獻[5-6]中有詳細推導(dǎo)，在此共形陣建模的基礎(chǔ)上，以全局坐標(biāo)系為參考，給出如下柱面共形陣列導(dǎo)向矢量：

(1)

u=sin(θ)cos(φ)X+sin(θ)sin(φ)Y+cos(θ)Z

(2)

|gi||pl|cos(θigk)=gi·ql=giθkθ+giφkφ

(3)

其中：Bi,i=1,2,…。D表示陣元位置坐標(biāo)矢量；u表示信源單位矢量坐標(biāo)；(θ，φ)分別表示信源相對全局直角坐標(biāo)的方位角與俯仰角；ri,i=1,2,…。D表示陣列中第i個陣元對入射信號源的響應(yīng)；gi表示陣元方向圖，kθ,kφ分別表示信源來波極化狀態(tài)。

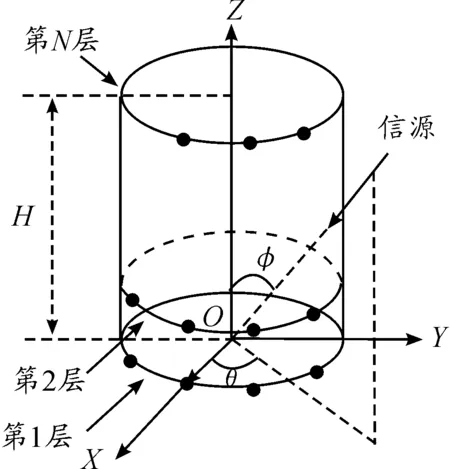
圖1 柱面共形陣列結(jié)構(gòu)

接收信號模型可以表示為

X(t)=A(θ,φ)S(t)+E(t)

(4)

各向量分別定義：

X(t)=[x1(t),x2(t),…,xD(t)]T

(5)

S(t)=[s1(t),s2(t),…,sK(t)]T

(6)

E(n)=[e1(t),e2(t),…,eD(t)]T

(7)

A(θ,φ)=[a(θ1,φ1),a(θ2,φ2),…,a(θK,φK)]

(8)

其中:X表示快拍數(shù)據(jù)模型，S表示陣列入射信號，E表示加性高斯白噪聲，A(θ,φ)表示柱面共形陣列流型矩陣。

2 柱面共形陣2-D DOA算法

通常情況下，實際感興趣的信源數(shù)是未知的，因此需要把可能存在的目標(biāo)區(qū)域內(nèi)的波達角度均分為G個掃描點，每個點對應(yīng)潛在的信源，對每個信源進行能量估計，得到能量譜，從而得到信源波達角度的估計值。實際上，G的取值往往遠大于區(qū)域內(nèi)信源的個數(shù)，導(dǎo)致S中大部分元素的數(shù)值是零，與此同時，其中的第k個非零列也對應(yīng)了位于(θk,φk)處的信源，因此稀疏類算可以適用于DOA估計。將式(4)整理為稀疏源接收疊加形式：

(9)

假設(shè)：

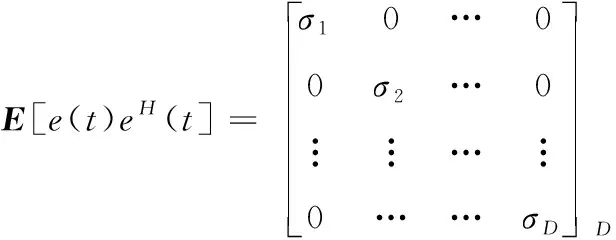
(10)

(11)

(12)

AH=[a1,…,aKI]=[a1,…,aK+D]

(13)

(14)

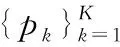
(15)

式中||·||表示矩陣的Frobenius范數(shù)，R-1/2為Hermitian矩陣R-1的正定平方根。式(15)可以改寫為如下形式[9]：

tr[(I-xxHR-1)(R-xxH)]=

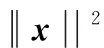
(16)

其中

(17)

可以看出式(16)、式(17)與下式等價：

(18)

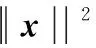
(19)

式(18)和式(19)是等價的，式(19)是一個加權(quán)l(xiāng)1范數(shù)約束問題，同樣也是一個凸優(yōu)化問題，構(gòu)造一個等價約束最優(yōu)化問題來求解式(19)：

(20)

利用拉格朗日乘子法求解式(20)，構(gòu)造代價函數(shù)：

J(Q,L)=tr(QHP-1Q)+tr(LH(I-QHA))

(21)

其中，L為拉格朗日乘數(shù)矩陣，求式(21)的梯度可得聯(lián)立方程：

(22)

(23)

聯(lián)立式(22)、式(23)可得：

L=(AHPHA)-1=R-1

(24)

將式(24)代入式(23)可得：

Q=PAR-1

(25)

將式(35)代入式(20)可得：

tr(xHQHP-1Qx)=tr(xHR-1x)

(26)

可以驗證式(19)與式(20)等價，而式(25)即為式(20)的解，上述推導(dǎo)也表明了對Q，P的循環(huán)最小化可使目標(biāo)函數(shù)式(20)快速收斂。

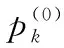
算法總結(jié)如下：

初始化：

迭代：

3 仿真實驗與分析

為驗證本文所提方法的有效性，對比2D-MUSIC算法展開實驗。為了不失一般性，設(shè)置如圖1所示的接收陣列，M=5、N=10，相鄰圓環(huán)的間距為d=λ/2；噪聲為加性高斯白噪聲；信號源個數(shù)K=2，且相互獨立；來波信號角度設(shè)置為θ1=30°，φ1=40°，θ2=35°，φ2=45°；信源極化狀態(tài)kθ=7,kφ=5；假設(shè)在DOA估計之前已對感興趣的區(qū)域有一定認(rèn)知，所以提前設(shè)定方位角掃描范圍為「25°，40°?，俯仰角掃描范圍為「35°，50°?，掃描間隔設(shè)置為0.5° ；根據(jù)以往文獻經(jīng)驗，迭代次數(shù)預(yù)設(shè)為10。單元方向圖設(shè)置參考文獻[5]：

當(dāng)0≤θ≤π/2時

(cosφ-jsinφ)

(27)

cosθ(sinφ-jcosφ)

(28)

其他，gθ(θ,φ)=gφ(θ,φ)=0

J0,J2分別是零階和二階第一類貝塞爾函數(shù)。

仿真實驗1：

設(shè)置信噪比(Signal to Noise Ratio,SNR)為15 dB，快拍數(shù)N1=2,N2=200。

仿真結(jié)果表明(圖2)：當(dāng)快拍數(shù)足夠大時，兩種算法都能成功地把兩個遠場信源分辨出來；而當(dāng)快拍數(shù)減小到2時，2D-MUSIC算法已經(jīng)失效，真實信號源的譜峰混疊在偽峰之中導(dǎo)致無法分辨出真實入射角度，但所提算法仍然可以分辨出兩個銳利的譜峰，且旁瓣水平較低，方位角和俯仰角的估計偏差也很小。

仿真實驗2：

定義實驗成功須滿足下式：

(29)

定義角度均方根誤差為

(30)

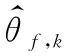
圖3(b)(d)設(shè)置快拍數(shù)N2=200，信噪比從-15 dB變化到15 dB；圖3(a)(c)設(shè)置信噪比為10 dB,快拍數(shù)從10變化到200，其他實驗條件不變。100次蒙特卡洛實驗觀察分辨成功概率和均方根誤差隨快拍數(shù)的變化曲線。

從圖3的實驗結(jié)果可以看出：隨著快拍數(shù)及信噪比的增加，兩種算法的估計精度逐漸提高，均方根誤差則逐漸減小，說明算法的性能在快拍數(shù)據(jù)充足，信噪比較高的情況下變現(xiàn)良好。但是當(dāng)快拍數(shù)與信噪比較低時，本文提出的算法估計誤差明顯小于2D-MUSIC算法，成功辨別出兩個信源的概率也高于2D-MUSIC算法。

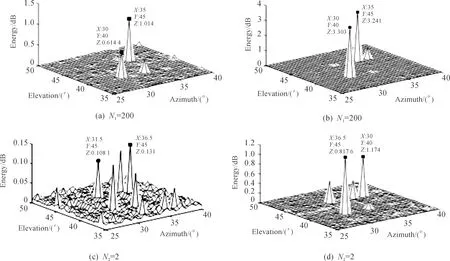
圖2 能量譜估計仿真結(jié)果 (a)(c)2D-MUSIC;(b)(d)所提算法

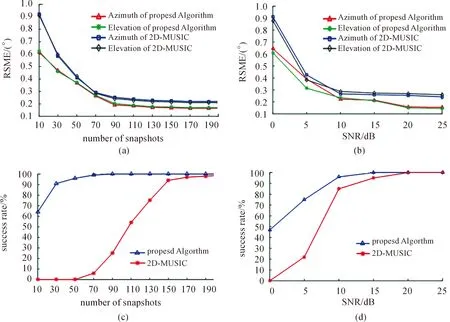
圖3 均方根誤差及成功概率實驗結(jié)果 (a)(c)快拍數(shù);(b)(d)信噪比

4 結(jié)論

將協(xié)方差稀疏迭代估計方法應(yīng)用到柱面共形陣2-D DOA估計上，實現(xiàn)了短快拍條件下的2-D DOA估計。所提算法充分利用了協(xié)方差矩陣的稀疏性，利用循環(huán)最小化方法解決全局最優(yōu)化問題。相比于傳統(tǒng)子空間類共形陣2-D DOA估計算法，本文的方法不需要額外選擇用戶參數(shù)，在短快拍、低信噪比的條件下，成功地分辨分布較近的遠場源，具有較高的估計精度，為解決短快拍條件下共形陣2-DDOA估計問題提供了重要思路。