多尾翼式高超聲速制導炮彈氣動布局設計與特性分析

朱 胤，王旭剛

(南京理工大學 能源與動力工程學院， 南京 210094)

近年來一些高超聲速武器，如電磁炮[1]、電熱化學炮[2]等，利用特殊的發射技術，將彈丸發射到5馬赫以上，實現了高超聲速和遠程飛行，具有飛行高度高、飛行速度快、飛行空域廣的特點，已成為當前軍工領域的研究熱點。但由于受發射方式和體積等諸多條件的約束，其飛行控制能力受到限制，給炮彈完成戰斗技術指標帶來了困難。因此，根據其發射方式、飛行特點等要求，進行氣動布局設計、尋求適配的氣動力工程算法并獲得其氣動參數，成為高超聲速制導炮彈實現遠程精確打擊的關鍵一步。

目前，國內外已有眾多研究機構對高超聲速炮彈開展了理論和試驗研究，包括其氣動外形和氣動特性等。國外學者Agnone和Zakkay[3]分析了尾椎對高超聲速炮彈的飛行特性以及氣動參數的影響，為高超聲速炮彈的氣動布局設計提供了借鑒思路；Stuart McIlwain等[4]對高超聲速飛行下彈翼的空氣動力學特性做出了研究，得出了彈翼表面阻力系數及熱流暢情況，對高超聲速彈翼的設計作出了理論參考。A D Dupuis和J A Edwards[5]利用飛行試驗和仿真計算，研究了“錐—柱—裙”組合體氣動外形的高超聲速布局，并討論了其氣動特性和熱流暢情況；呂水燕、張傳俠等[6]通過數值模擬獲得了高超聲速下雙橢球體經典模型的熱流密度，為高超聲速飛行器的熱流計算提供了重要參考；孫祥程、葛暢[7]采用基于RANS的CFD數值計算方法，開展了高超聲速翼型的氣動特性設計與研究，并設計了兩種具有更加優良的低速、跨聲速氣動特性的高超聲速翼型。

高超聲速炮彈的外形取決于諸多因素，需對其進行氣動力預測。相比于數值算法，工程算法計算周期短、制作成本低，適用于高超聲速的氣動力工程算法包括激波-膨脹波法、切楔/切錐法、牛頓理論等等[8]。牛頓理論將流體假設為規則運動的流體微團以平行的直線軌跡流向物面，可直接計算出對應的法向和軸向力系數；其內涵簡捷、工程量小，可用于快速可靠地計算高超聲速制導炮彈的氣動參數。

本文針對高超聲速的氣動布局特性，在已有高超聲速炮彈理論研究的基礎上，設計了一種“一”字平面鴨舵控制的尾翼式高超聲速制導炮彈的氣動布局，選取了適配的高超聲速工程算法對其進行了氣動計算，并對計算方法作出了改進；得到了相應氣動參數且分析了其氣動特性的變化趨勢。

1 氣動布局設計

1.1 頭部外形和彈身彈尾設計

1) 頭部尺寸及母線。炮彈的頭部阻力受其彈型系數的影響，適當增加頭部長度可減小空氣阻力，增大頭部容積，故取彈頭部長度為3.5d。常見的頭部母線有錐形、圓弧形、拋物形、指數形以及馮卡門形等，其各自的氣動特性見文獻[9]。基于它們各自的阻力特性，本文對這幾種母線進行了對比，得出高超聲速制導炮彈宜采用阻力較小的指數形或馮卡門形。而馮卡門形母線相對于指數形母線具有更大的頭部容積和容積利用率，故馮卡門形頭部母線為最適合本文設計的頭部母線形狀。

2) 頭部鈍化。高超聲速下需將彈頭鈍化以減小氣動加熱，本文在鼻尖處用半徑為n的半球狀頭部代替原有的尖頭。文獻[10]通過對某彈型在高超聲速條件下的實驗結果和理論計算得出，當頭部鈍度取n/R=0.03時，頭部鈍化后對波阻沒有影響。

高超聲速下彈身的阻力極大，設計彈身長細比λb時應從阻力最小的角度出發；在超聲速以及高超聲速的條件下，船尾對阻力的減小有輕微幫助，但尾椎的角度不宜過大，否則會因尾椎效應導致后部氣流分離。綜合考慮彈體結構、剛度、工藝以及設計要求等條件后，本文選取彈身長細比λb=5，尾部長細比λta=3，尾部收縮比d/D=0.8。

綜上所述，本文設計的制導炮彈總長細比λ=11.5。全彈尺寸如圖1所示(單位：mm)。

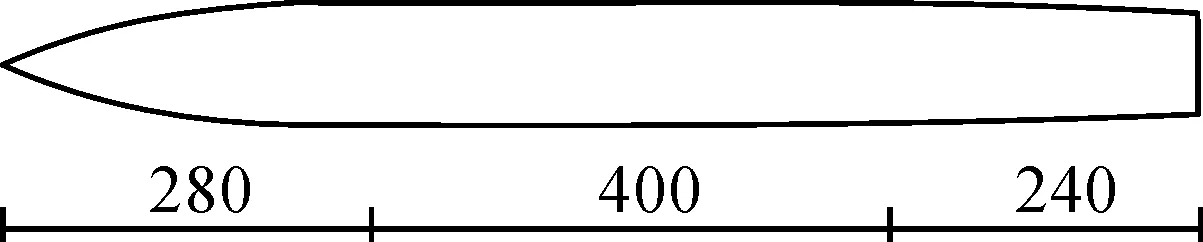
圖1 彈體尺寸示意圖

1.2 尾翼和鴨翼設計

尾翼有4片、6片和8片的布置形式，需根據穩定性要求確定翼片數量。尾翼設計時需要考慮翼平面形狀、翼剖面形狀、翼面面積等問題。

1) 翼平面形狀。高超聲速下，三角形翼的升阻比較大，壓心變化范圍小，是較為理想的超聲速翼型。但相對于三角翼，梯形翼能夠保證翼尖有足夠的結構剛度，并有利于部位安排，故尾翼可選用小展弦比的梯形翼。

2) 翼剖面形狀。考慮強度、剛度和氣動力特性等要求，雙弧形翼在高超聲速下的波阻系數最小[11]，故高超聲速制導炮彈的彈翼應采用雙弧形剖面翼。另外，為減小氣動熱，翼前緣也應設計為鈍頭前緣。

3) 翼面面積。彈翼面積的設計主要取決于機動性和射程等要求。對于尾翼，初步設計時可按下式計算其面積S：

(1)

式(1)中：ny為需用法向過載；q為動壓。為了滿足靜穩定要求，采用8片尾翼的布置形式。

鴨翼的設計要求與尾翼類似，高超聲速下，同樣用大根梢比梯形翼代替三角翼。按照控制力矩方程求舵的面積，有

(2)

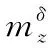
2 氣動特性工程計算

牛頓撞擊理論的示意圖如圖2。牛頓模型假設了所有流體微團都以平行的直線軌跡流向物面，沒有任何不規則運動。而實際上作宏觀運動的氣體是分子的不規則運動與一種定向運動的合成，這種不規則運動由自由流的靜壓p∞來度量。因此，物面單位面積上的法向力應解釋為與p∞的差，即

(3)

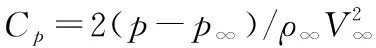
Cp=2sin2θ

(4)

式(4)稱為牛頓正弦平方定律，此式說明，壓強系數與物面切線和自由流夾角正弦的平方呈正比。得出壓強系數后，可通過積分求得相應的氣動力系數。

圖2 牛頓撞擊理論示意圖

按照牛頓理論，細長尖拱形頭部可用內接圓錐頭部來計算[12]，當α<θc時，頭部升力系數為

CL=cos2θcsin2αcosα-[2sin2θc+sin2α(1-3sin2θc)]sinα

(5)

其波阻系數為

CD=CNsinα+CAcosα

(6)

式(6)中：CN為法向力系數，CA為軸向力系數。頭部壓心系數表達式為

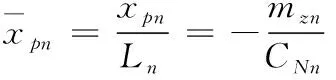
(7)

對于尖拱形頭部

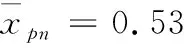
(8)

本文設計的制導炮彈采用了小尾椎角的船尾結構。計算全彈阻力時，應單獨計算尾部的壓差阻力，然后并入全彈阻力。而尾部因小尾椎角而造成的阻力影響極小，可以忽略不計，且不影響結果的準確度。

本文計算氣動參數時將尾部視為圓柱，并入彈身，將整個彈體(除頭部以外)視為圓柱后體，將彈身和尾部的長細比相加，視為圓柱后體長細比。這樣，在計算各項氣動參數時，只需要計算圓柱后體的氣動參數，無需再單獨計算船尾的氣動參數。這一改進減少了計算量，簡化了彈體氣動參數的計算過程。在高超聲速下，圓柱后體的升力系數可用牛頓理論加離心力修正的方法得到：

(9)

式(9)中：λC為圓柱后體的長細比。

圓柱后體的摩阻可按下式估計：

(10)

式(10)中：SC為圓柱后體表面積；SB為圓柱段彈體截面積；Re為邊界層外緣處的雷諾數。

彈體底部阻力可由E.U.Fleeman提供的無動力滑行彈身底部阻力系數公式估算：

(11)

不考慮黏性干擾，由攻角產生的升力沿圓柱后體均勻分布，故圓柱后體的壓心位于：

(12)

式(12)中：LN為頭部長度；LC為圓柱后體長度。

3) 彈翼空氣動力系數。彈翼壓心位于其平均氣動弦的中點，對于雙弧形剖面翼，其升力系數為

(13)

雙弧形彈翼的阻力系數為

(14)

3 仿真校驗

為了驗證本文所選計算方法的正確性，基于本文算法計算并分析了文獻[10]中所給出的一種無翼式錐-柱型結構彈體的激波阻力系數Cdw、摩擦阻力系數Cdf和底部阻力系數Cdb。該彈型的頭部長細比為3.5，圓柱后體長細比1.5，根據計算結果作出如圖3所示的曲線。計算摩阻時，取空氣的溫度T=293 K，密度ρ=1.205 kg/m3，動力黏性系數μ=1.82×10-5Pa·s，聲速a=343 m/s。

用本文方法計算出的各項阻力的分布及大小與原文獻中給出的結果具有相當的一致性。其波阻系數幾乎不隨Ma變化；摩阻系數隨Ma的增加而減小；底阻在低馬赫時所占比例較大，且隨Ma的增加而逐漸減小；波阻占總阻力的比例隨Ma的增加而增加。整個計算結果與原文結果相比，誤差均在可接受的范圍內，與原文中實驗結果吻合較好。因此，本文所用的計算方法能夠可靠地獲得高超聲速制導炮彈的氣動力特性。

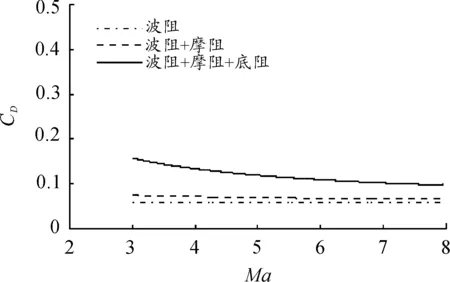
圖3 計算結果曲線

3.1 氣動布局設計結果

通過分析及計算，得出梯形尾翼的面積Sw=1.95SB，半展長51 mm，根弦長257 mm，梢長129 mm。本文設計的高超聲速制導炮彈的氣動布局如圖4所示。

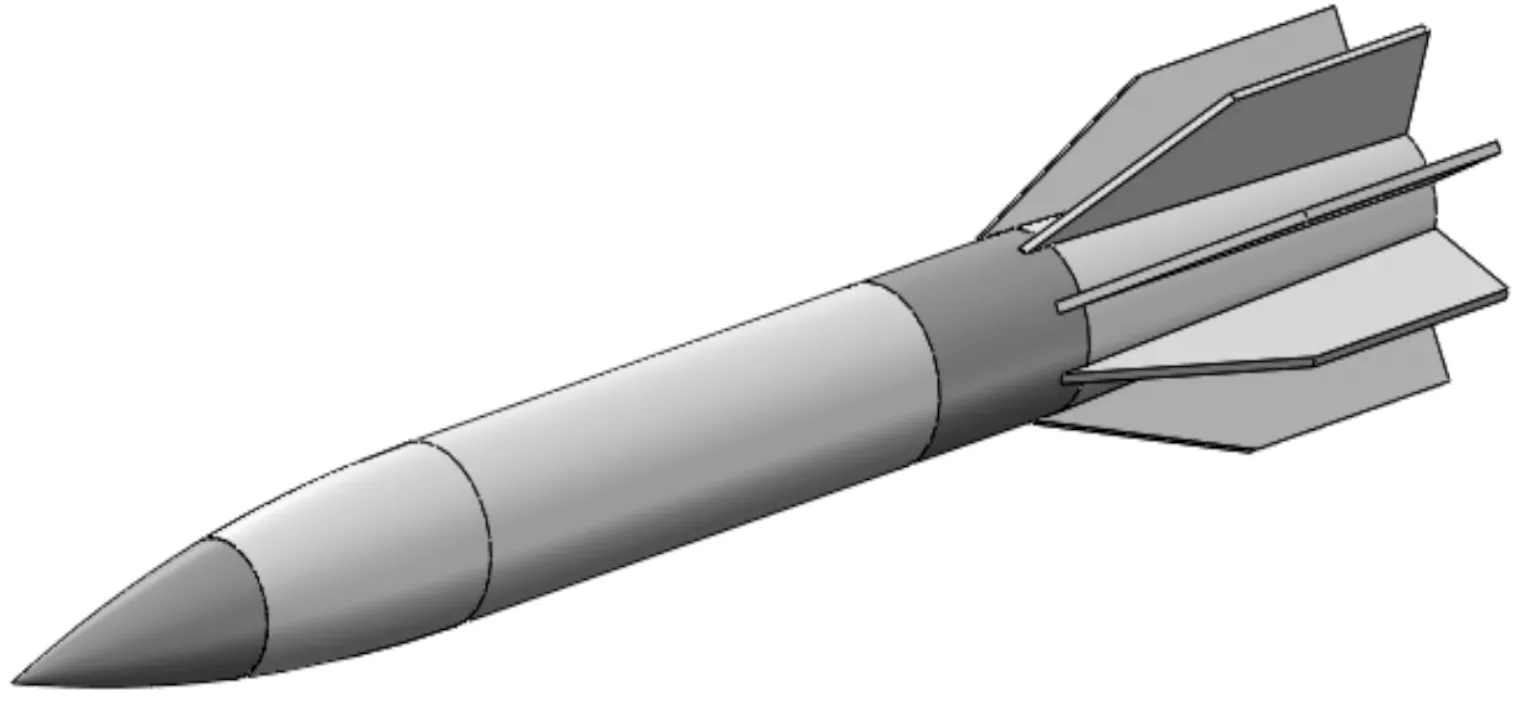
圖4 八尾翼式高超聲速制導炮彈氣動布局

通過計算得鴨翼面積Sr=0.24SB，半展長45 mm，根弦長43.5 mm，根梢比5。壓心位置距頭部頂點的距離xr=140 mm。張開鴨舵后的外形如圖5所示。

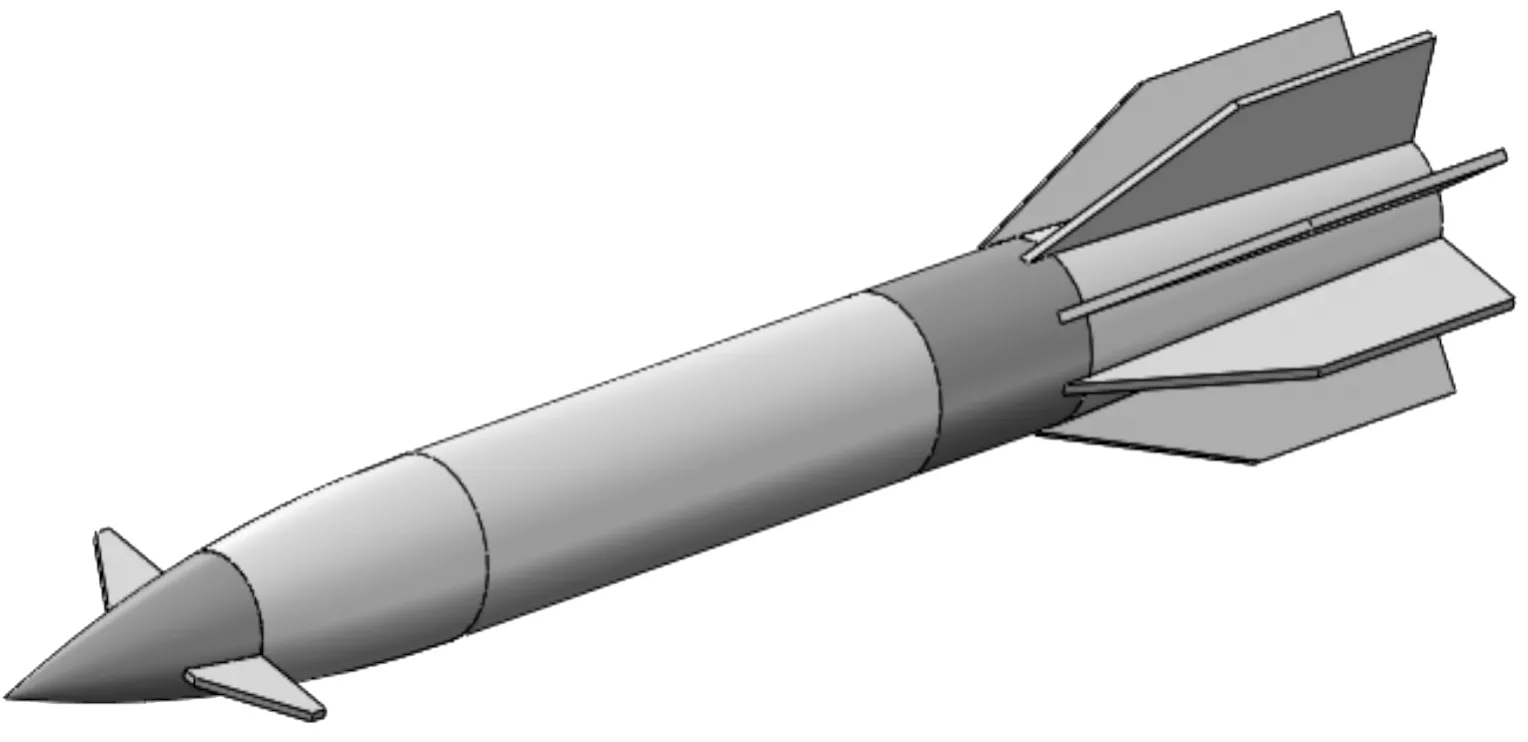
圖5 鴨舵式高超聲速制導炮彈氣動布局

3.2 氣動力計算與分析

根據牛頓理論計算出的彈體在高超聲速條件下的升力系數CL與攻角α和馬赫數Ma的關系曲線如圖6所示。從圖6可以看出：高超聲速下制導炮彈的升力系數CL隨攻角α的增加而增加，隨馬赫數Ma的增加而減小。升力隨攻角和馬赫數的變化均為非線性的，隨著攻角的增加，升力系數的變化越來越明顯，反之，馬赫數的增加對升力系數的影響則越來越小。

圖6 升力系數與攻角和馬赫數的關系曲線

圖7為該制導炮彈在高超聲速下的阻力系數CD與攻角α和馬赫數Ma的關系曲線。阻力系數的變化規律同升力系數相同，也是隨攻角α的增加而增加，隨馬赫數Ma的增加而減小，且變化趨勢亦為非線性的，馬赫數Ma越高時對阻力的影響越小。該結果與文獻[10]中給出的錐-柱-船尾型布局的阻力實驗結果一致。

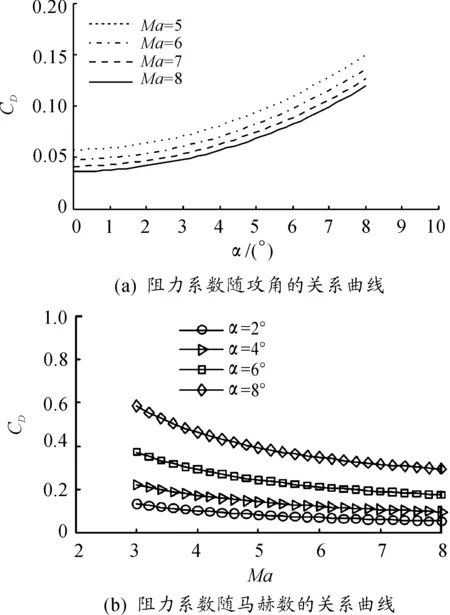
圖7 阻力系數與攻角和馬赫數的關系曲線

圖8 操縱力矩系數與舵偏角的關系曲線

圖9 縱向靜穩定系數與馬赫數的關系曲線

圖10為張開鴨舵前全彈穩定裕度η曲線，圖11為該彈張開鴨舵后與張開鴨舵前穩定裕度比值η2/η1的曲線。

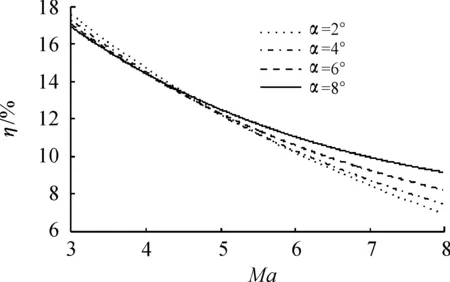
圖10 張開鴨舵前的穩定裕度曲線

圖11 張開鴨舵后與張開鴨舵前穩定裕度之比曲線

結果表明：本文設計的高超聲速制導炮彈在Ma=7.3，α=8°時的穩定裕度為9.7%。在Ma>5的高超聲速條件下，該制導炮彈的穩定裕度η隨攻角α的增加而增加，隨馬赫數Ma的增加而減小。張開鴨舵會使穩定裕度減小，在α=8°、Ma=5時張開鴨舵會使穩定裕度下降17%；鴨舵張開后與張開前穩定裕度的比值隨攻角α的增加而增加，隨馬赫數Ma的增加而減小。穩定裕度η的大小可以通過改變彈體外形的方式來調整，在同一馬赫數下，η隨尾翼面積、圓柱后體長度的增加而增加，隨彈頭部長度、鴨舵面積的增加而減小。

4 結論

本文采用了改進的氣動力計算方法：將彈身、彈尾視作圓柱后體，一并計算氣動參數，縮小了計算量，并計算了全彈的升力系數、阻力系數、操縱力矩系數、靜穩定系數和穩定裕度。升力、阻力系數均隨攻角的增加而增加，隨馬赫數的增加而減小；操縱力矩系數隨舵偏角的增加而增加；靜穩定系數小于零，該彈為靜穩定彈；高超聲速下穩定裕度隨馬赫數的增加，隨攻角的增加而減小。計算結果表明：本文設計的高超聲速制導炮彈可控性良好，滿足設計要求。