爆炸環境下車輛底部V型結構多參數優化研究

徐克非，王顯會，周云波，胡文海，張 明

(1.南京理工大學， 南京 210094；2.東風汽車汽車公司技術中心， 武漢 430056)

防護型車輛除了應對槍彈襲擊外，更大的威脅來自地雷和簡易爆炸物自下而上的爆炸沖擊，車輛底甲板容易發生變形、破裂等損傷，對車輛和車內乘員安全造成很大的威脅。為了減少爆炸沖擊給車內乘員帶來的傷害，同時減少設計成本，加快設計進程，現在多采用有限元仿真技術設計。將多物質單元算法(ALE)與流-固耦合算法[1](FSI)相結合，能提高爆炸沖擊波和乘員響應的仿真精度。Kevin Genson[2]針對炸藥掩埋深度以及V型靶板不同角度對爆炸條件下的結構響應進行了研究；A.Neuberger[3]針對爆炸條件下的靶板響應設計了試驗臺架，驗證不同靶板在爆炸條件下的結構響應；韓輝等[4]從地雷的傷害原理入手，分析不同反車底雷的毀傷效應，并根據應對不同地雷的多種防護原理，列舉了多種底部防雷技術和具體防護措施的發展現狀。張中英等[5]對簡化V型結構進行仿真研究，得出V型結構在減小地雷對車輛底部的破壞方面具有優勢，并進一步研究得到了V型結構角度與車身垂直加速度衰減的關系。針對大規模仿真優化問題，國內外目前已形成了基于實驗設計、響應面法的多參數優化(MO)[6]。MO具有計算精度高的優點，但是計算時間長，占用資源多，樣本數量多，為縮減計算時間，工程中常通過參數篩選[7](如靈敏度、貢獻度分析等)，將一些在設計中不占主導作用的參數剔除，僅保留對結果起最大影響的一個或幾個參數，減少實驗設計的樣本數量。

本文結合FSI與ALE仿真算法[8]，對爆炸沖擊作用下的某型車V型結構進行仿真分析與優化。通過臺架爆炸實驗驗證臺架結構仿真結果并對標。目標響應選擇為降低V型結構質量、減小結構變形撓度和底板剪應力，變量選取為V型結構的底板厚度和幾何形狀。建立多目標優化模型，采用帕累托(Pareto)優化方法，對底部V型結構進行優化設計。

1 V型底部結構響應仿真

基于某型車底部結構建立對應V型結構臺架有限元模型，根據車輛實際重量對臺架結構進行配重。建立覆蓋整個結構的空氣流場[圖1(a)中410尺寸的下尺寸界線以上的網格)和土壤(圖1(a)中410尺寸的下尺寸界線以下的的網格]，地雷替代物當量為6 kg TNT(STANG4569的2級防護標準[9])。地雷替代物置于試驗臺架正下方，淺埋地下100 mm，初始狀態下V型結構最低點距離地面為410 mm。采用ALE與FSI算法相結合，應用初始體積法模擬地雷替代物，仿真模型包括空氣、土壤、地雷替代物、臺架模型。

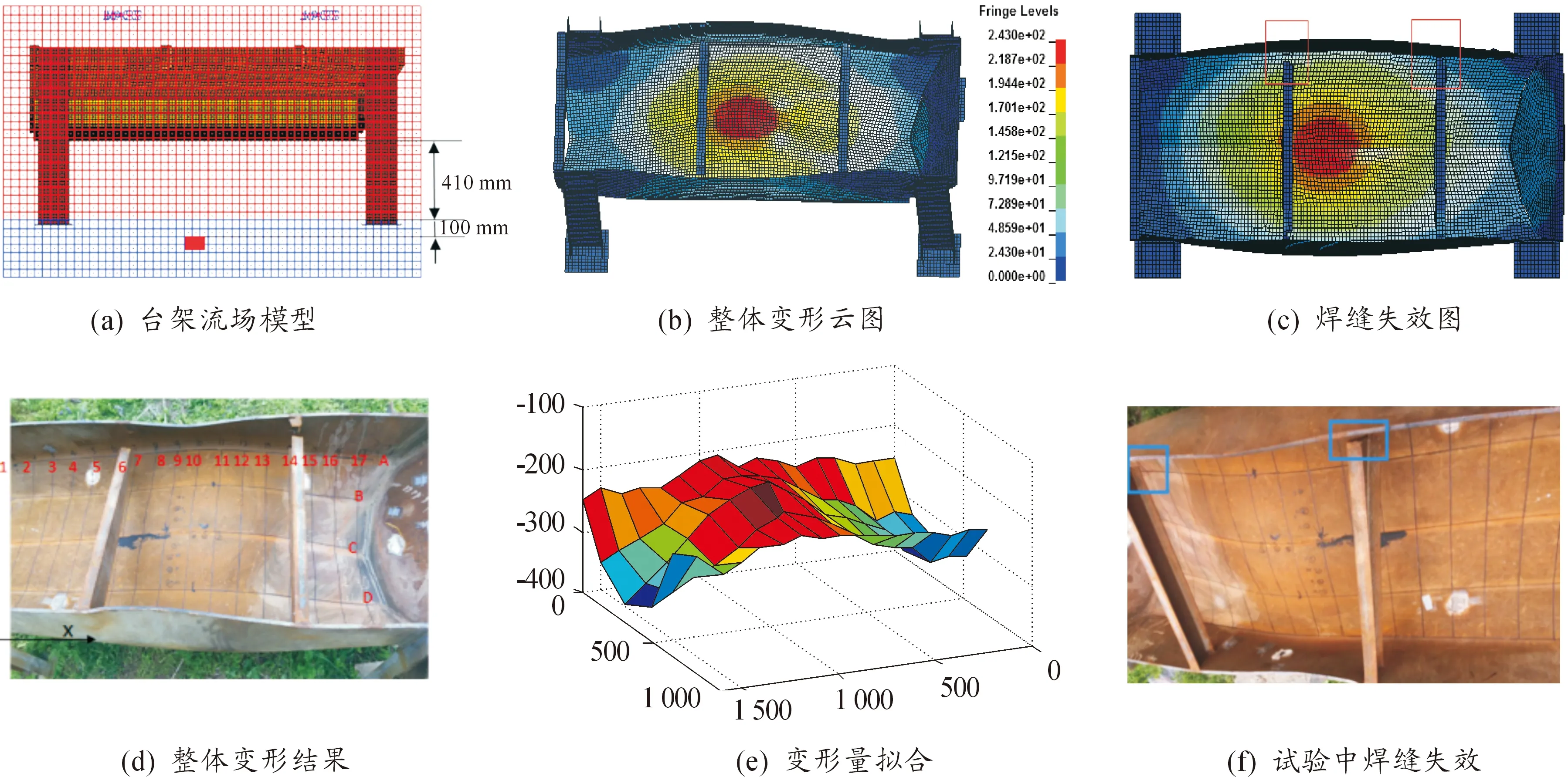
圖1 某型防護型車輛底部V型結構仿真分析

對V型結構臺架進行爆炸實驗，實驗各關鍵參數與仿真一致，地雷替代物符合實驗要求。爆炸實驗結果如圖1(d)，底部V型結構位于炸藥正上方的變形最大，試驗后對底板變形進行測量，把測量結果進行擬合，得到變形后的擬合形狀如圖1(e)。經測量，最大變形量為230 mm，與仿真測得的底板變形量243.4 mm相差不大，仿真計算值與試驗誤差為5.8%。仿真過程中底板側圍發生較大變形使得橫梁與底板的焊接處焊縫失效如圖1(c)，與試驗結果的焊縫失效如圖1(f)形態基本一致。綜上分析，對比仿真與試驗，底部結構的破壞形態近似，變形量差別不大，仿真精度滿足工程需求。

2 V型防雷組件優化算法研究

2.1 多目標遺傳優化算法

多目標優化特點在于存在多個優化目標，從而導致其解不確定為唯一值，而是構成一個解集，即最優解集，使用Pareto最優思想對該解集進行篩選。所謂Pareto最優就是，不可能通過優化其中部分目標而其他目標不至劣[10]。多目標遺傳算法(MOGA)可以處理有約束的多目標優化問題，并提供一系列Pareto解(Pareto-optimal solution)，適合本文的研究需求。

多目標優化領域中廣泛采用的MOP(Multi-Objective Optimization Problem )問題的數學定義如下：

Minimizeyy=f(x)={f1(x),f2(x),…,fm(x)}

Subjectto:e(x)=(e1(x),e2(x),…,em(x))≤0

Where:x=(x1,x2,xn, …,xn)∈X

y=(y1,y2,…,yn)∈Y

(1)

式中：x為n維設計變量，X為可行解集，y是目標向量，Y是目標向量y形成的目標空間，決策向量的可行取值范圍由約束條件e(x)確定；m為目標響應函數的個數；n為約束條件個數。

在結構優化問題中，多目標遺傳算法可計算出搜索范圍足夠大的Pareto最優解集，當決策者在該解集中結合實際條件選取最優解時，能最大可能覆蓋最優解。

2.2 標準邊界交叉法

標準邊界交叉(NBI)法[11]是由Das等人提出的一種新的尋優方法，在求解高維優化問題方面效率高。NBI法的搜索域公式如下所示：

(2)

(3)

式中：Ni為第i個優化目標的Pareto解去量綱標準化結果；bu、b1為標準化邊界的上下邊界；Oi是第i個目標的Pareto解；Oi_max是第i個目標的Pareto解集中的最大值；m為目標函數的個數；Rp為搜索半徑，在n維空間中可以選用R1、R2和R+∞。使用式(2)、式(3)可計算所需的Pareto解集的搜索半徑。

2.3 臺架優化數學模型

底部V型防護組件主要根據V型結構對爆炸沖擊波的偏置效應和V型結構對組件剛度的加強作用，實現較強的防護能力。因此V型結構V角角度、材料厚度等因素對V型結構的實際防御能力具有極大的影響。本次優化的目標是在保證結構總重量增加不大的同時，提高V型結構在爆炸沖擊下的防護能力。首先建立V型結構的臺架優化數學模型，如圖2所示，從而做到定量分析其抗爆炸沖擊性能。在該算例中，將V型結構總質量m，內板能量吸收E，底部最大變形x，焊接區域單元剪應力σXY為目標函數。將影響V型結構抗爆轟性能最大的外底板厚度t1、內底板厚度t2、底部V型角度θ，側壁距離l設置為設計變量，如圖3所示。

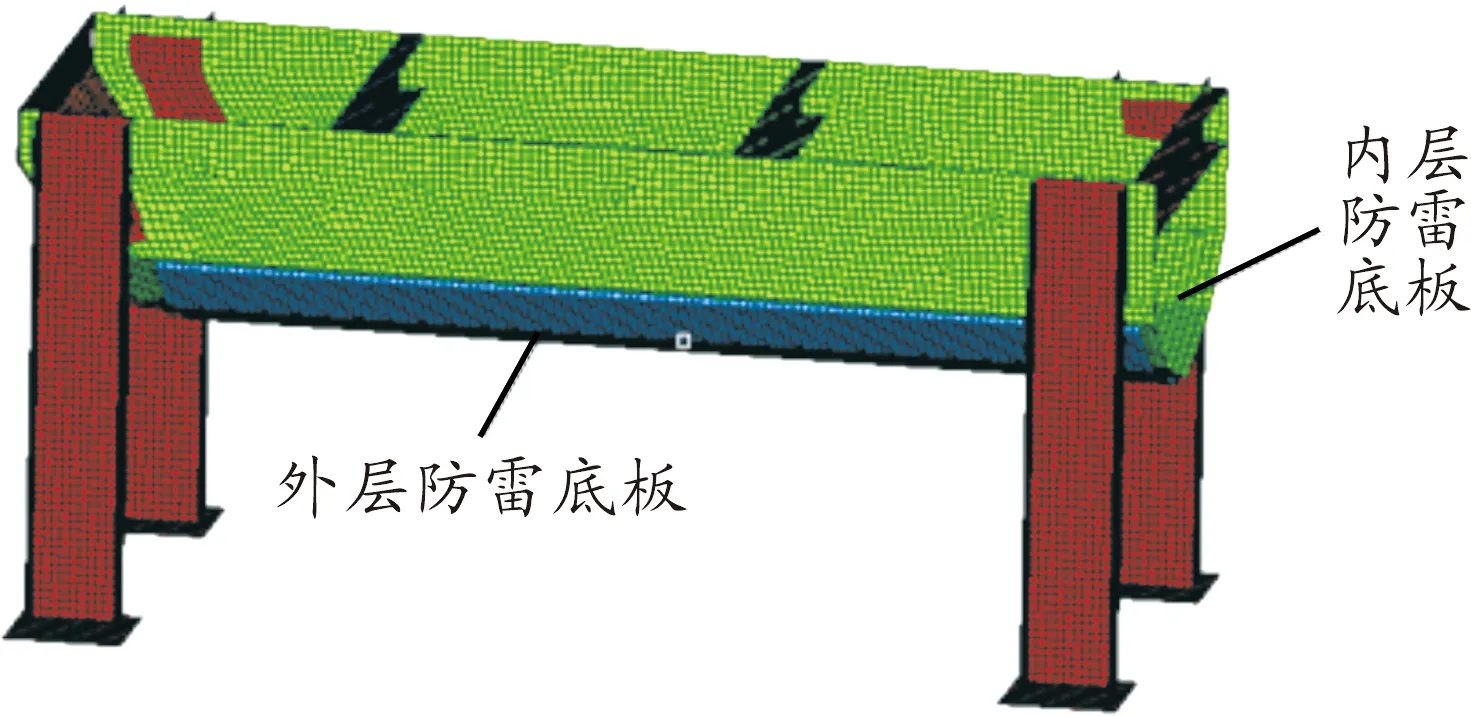
1.外層防雷底板; 2.內層防雷底板

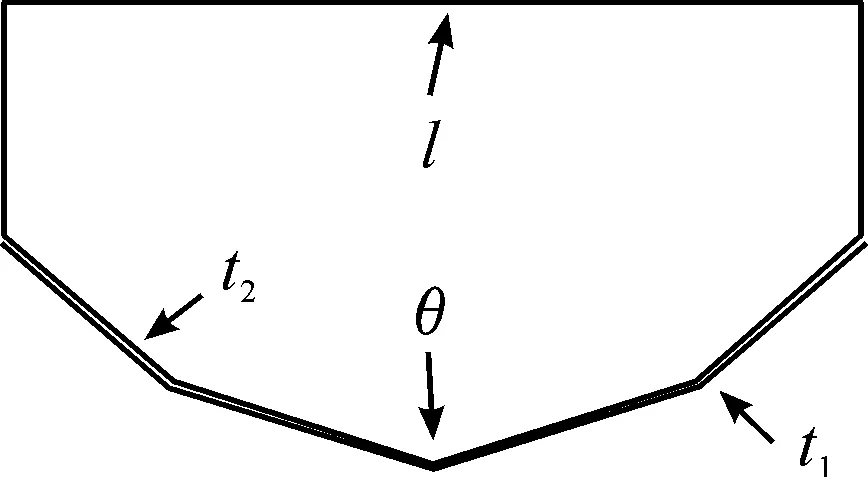
圖3 設計變量分布示意圖

根據結構設計狀態，從工程實際來考慮，臺架的優化設計變量在一定的范圍內變化，具體的設計參數范圍以及目標響應的仿真初值見表1和表2。

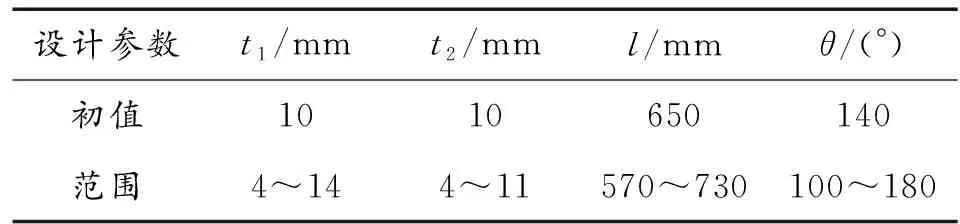
表1 底部結構設計變量

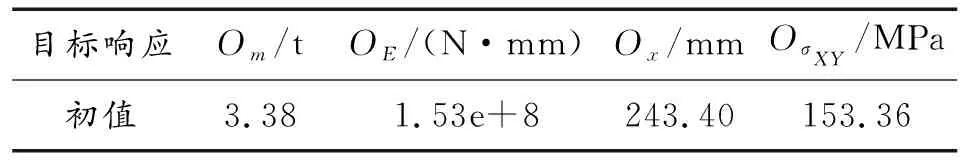
表2 底部結構目標響應初值

由于V型底部防雷組件底板設計中，Om、OE、Ox、OσXY都是越小越好，目標函數f(x)在優化設計中取極小值，因此本優化問題的數學模型可以寫成：

minf(x)={m,E,x,σXY}

(4)

(5)

其中l變量為雙向獨立變化，兩側邊可以向左右兩側變化，相當于2個形狀變量，因此，模型可以看作存在5個設計變量。在數據采樣試驗時，建立因子數為5，水平數為5的拉丁超立方采樣試驗S21(55)。根據所得的21組仿真結果通過最小二乘法可得到相應函數的二次多項式方程組，進而得到關于4個目標函數的響應面。

3 優化結果分析

3.1 Pareto解集

對底部V型防護組件臺架的優化數學模型進行求解。考慮模型可看作有5個設計變量，為了保證Pareto解集能夠充分合理描述其空間曲面，在設置遺傳算法參數時，將Pareto解的個數設置為 4 309個，遺傳代數設置為50代，每代精英數量占樣本總空間的10%，設置變異率0.1%。得到4目標函數通過遺傳算法求得的Pareto解Om、OE、Ox、OσXY。使用標準邊界交叉法對Pareto解進行去量綱標準化，上邊界bu=0.2，下邊界b1=1，使得標準化后的Pareto解落在從0.2到1的空間邊界內。

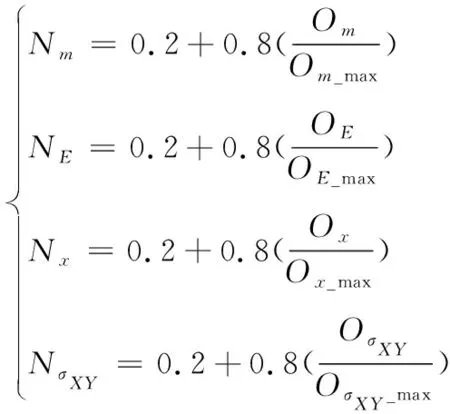
(6)

為獲得最適合的優化方案，需確定合適的尋優策略。在臺架優化設計中，認為最終的4個優化目標的權重相同，結合計算得出的 4 309個Pareto解，通過式(3)計算搜索半徑R2。計算部分結果見表3，可以看出最小搜索半徑為第1 584組解，可以認為第1 584組解是本次優化計算中，在各優化目標權重相同的情況下的最優方案(見表4)。

方案1 584在使3個目標都達到較好的結果的同時，總質量增加很小，可以認為沒有犧牲任何一個優化目標的情況下，達到了優化整體設計目標的目的。

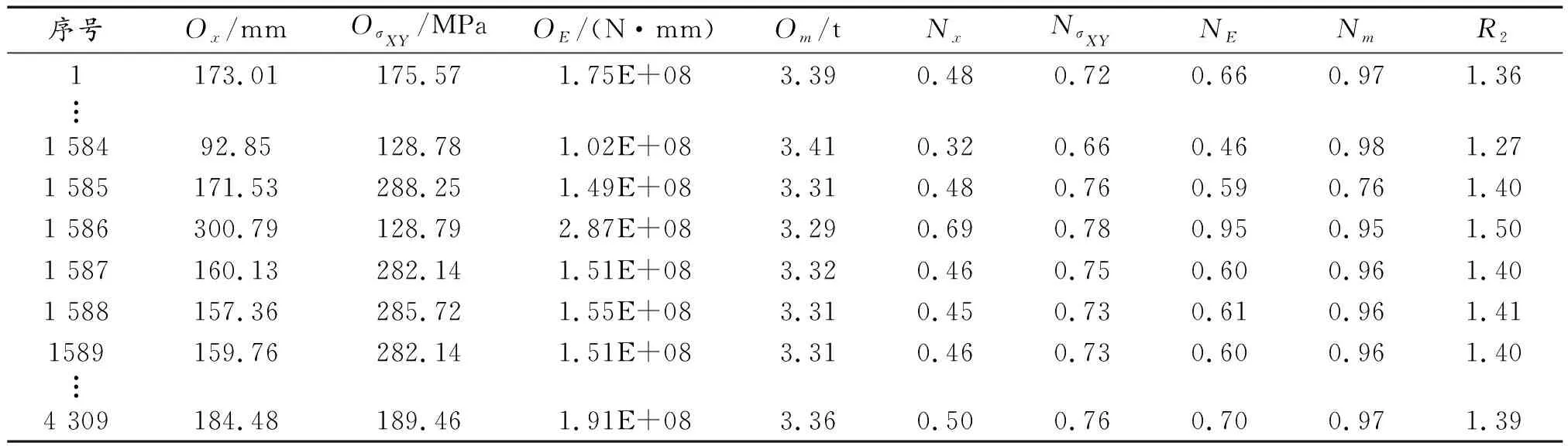
表3 部分Pareto解及對應標準化結果

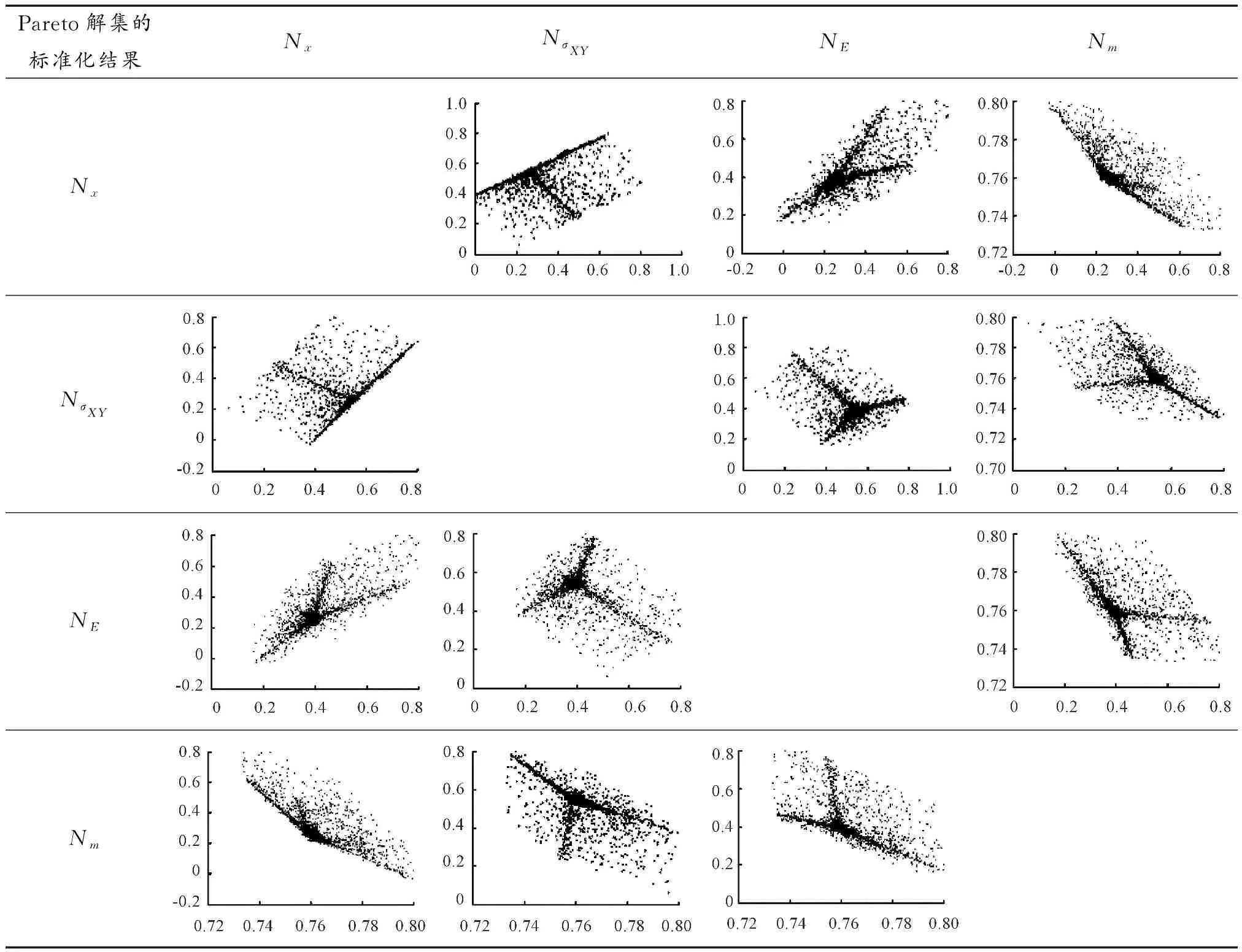
表4 部分標準化后的Pareto解集

3.2 Pareto結果分析與驗證

由于優化結果是通過響應面模型(代理模型)計算得到的預測值，為了驗證預測結果是否真實可信，須進行檢驗。將響應面模型的優化結果代入到前面的臺架試驗CAE模型中，由于臺架模型已與試驗實際進行對標，可以認為其提供的邊界條件仍然是可信的。修改后的臺架模型如圖4，臺架底部最低點到地面距離仍為410 mm。

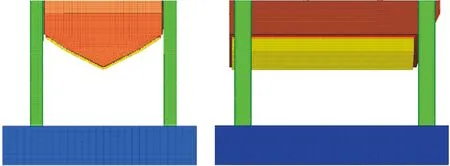
圖4 優化驗證CAE模型

對臺架模型進行仿真計算分析，可繪制如圖5所示位移云圖、位移曲線和圖6所示的內能曲線。由圖可知，在改變底板厚度、增大夾角角度后，防護組件的底部剛度明顯增大，變形最大的區域由原先集中于V型夾角中部分散到V型夾角兩邊。臺架吸收的能量相比原先更少，證明優化后的V型結構偏置效應更明顯。研究單元剪應力時，仍然選擇獲取初值時選定區域的單元，其中最大單元剪應力為135.02 MPa。

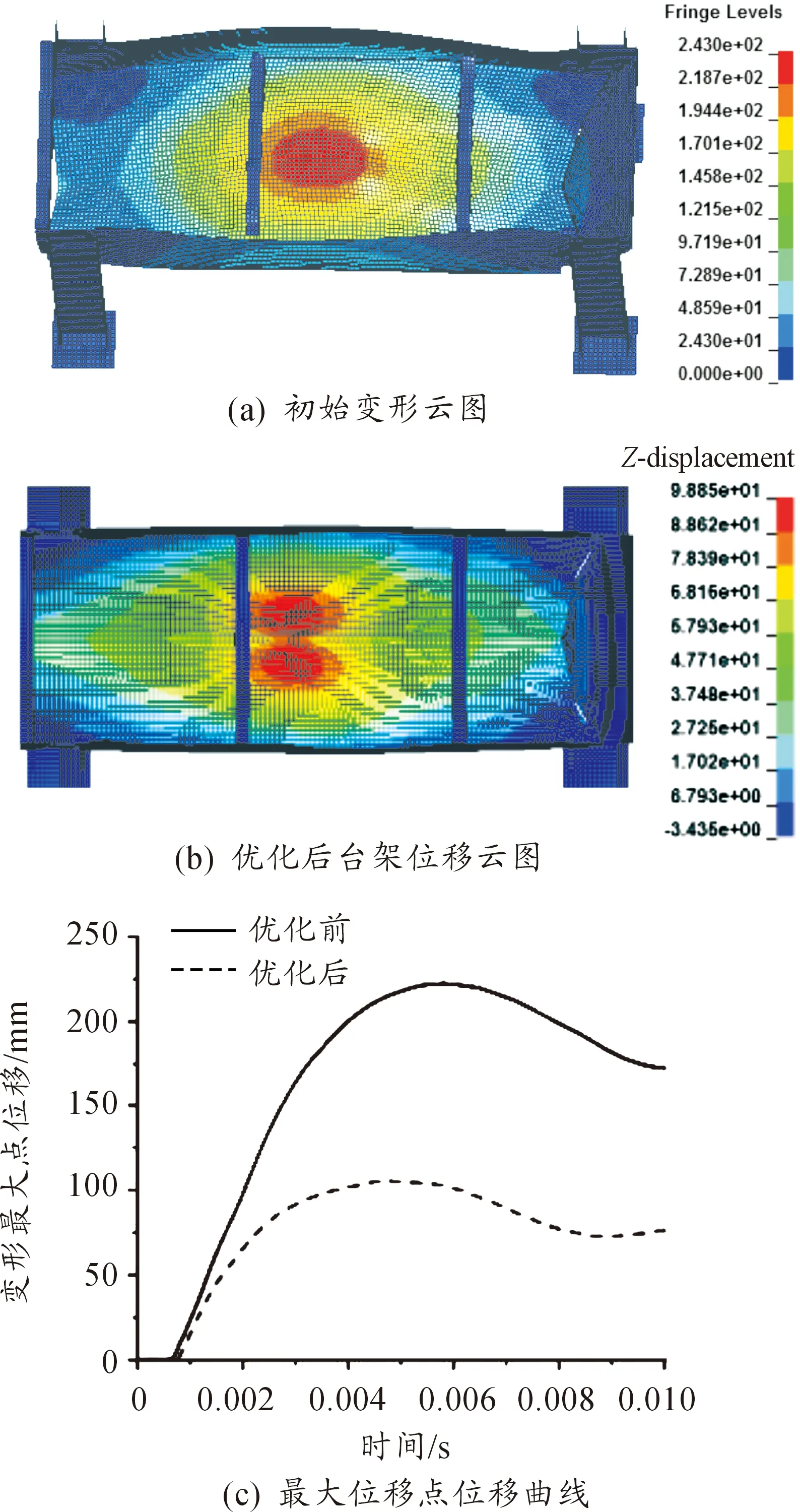
圖5 臺架模型位移云圖和位移曲線

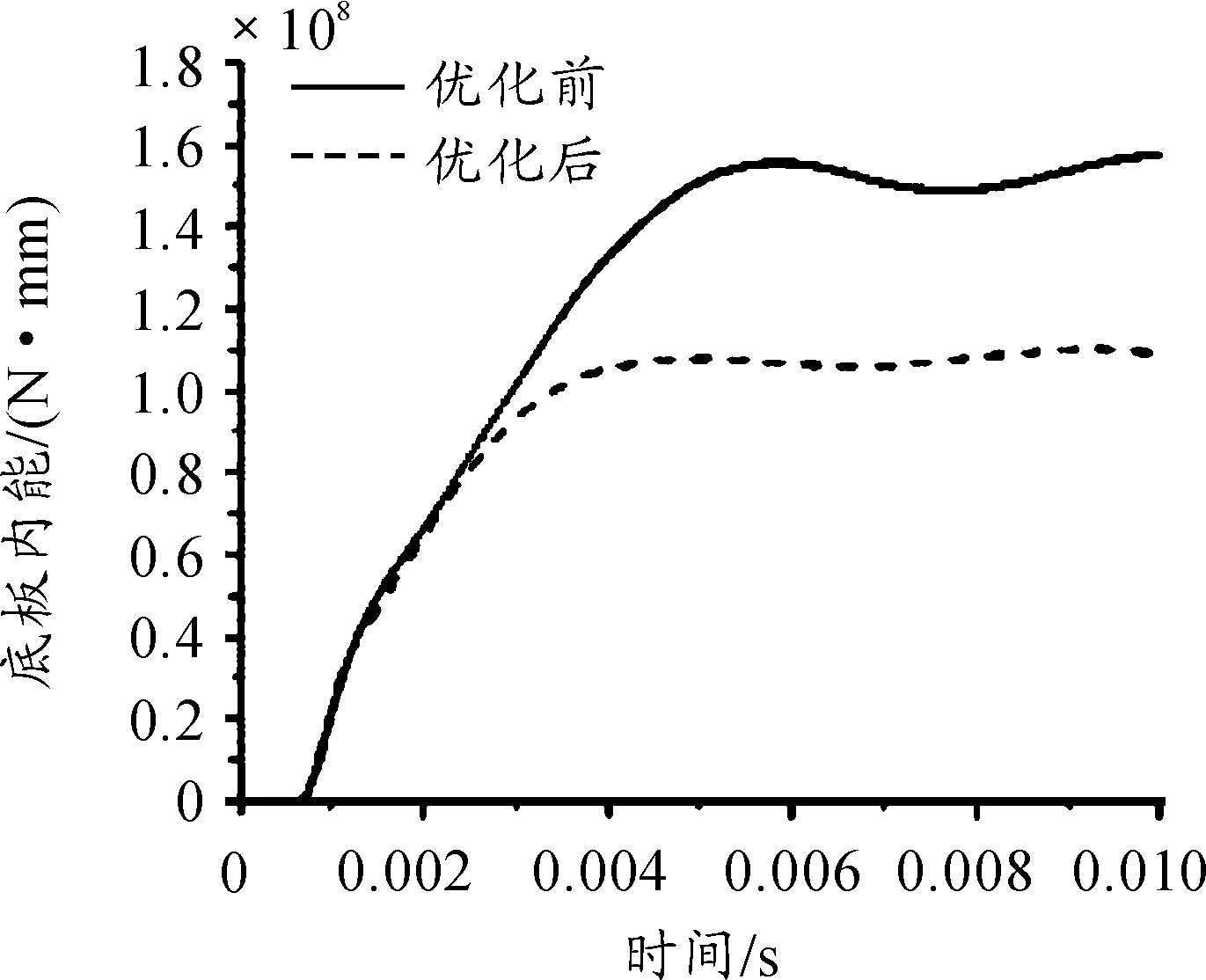
圖6 臺架模型內能曲線

綜合以上仿真驗證數據，仿真值與優化擬合的預測結果相對誤差在10%之內，最終認為仿真結果與預測結果誤差在工程誤差范圍內，預測結果可信。從上述驗證數據中可以看出Om變化量很小，根據表5，在犧牲了8.8%質量的基礎上，V型防雷組件在6 kg TNT爆炸條件下，變形撓度Ox減小59.39%，單元剪應力減小11.96%，內底板吸能減小27.45%。

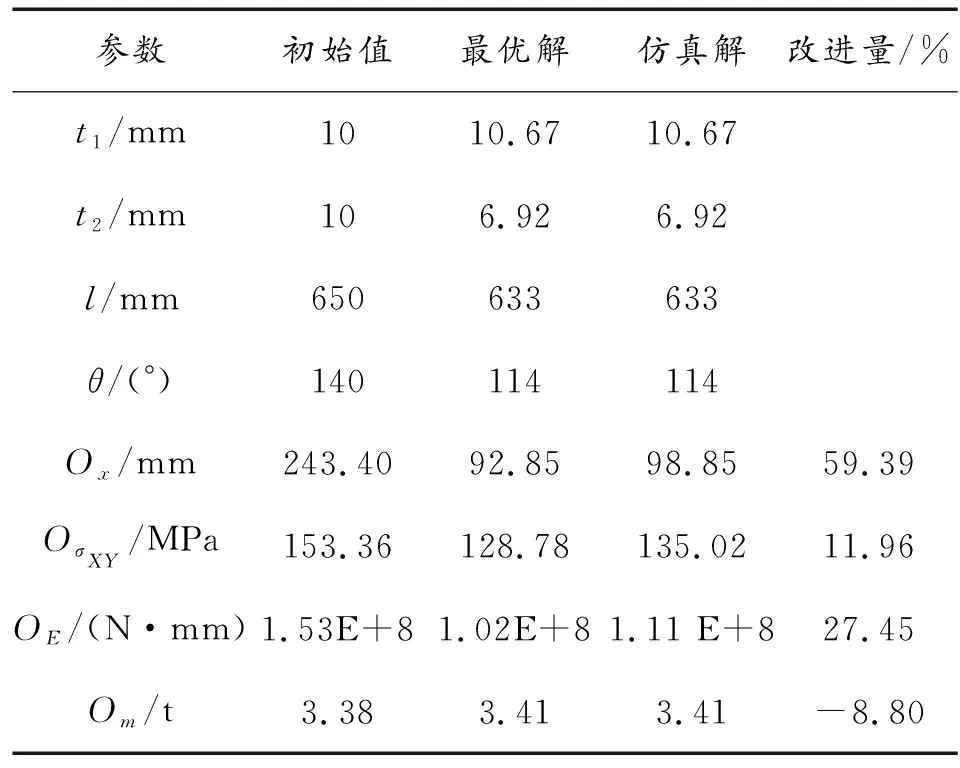
表5 優化前后V型防雷組件爆炸沖擊響應

4 結論

1) 利用ALE與FSI仿真分析，可以準確模擬在爆炸沖擊作用下的臺架結構響應，有效降低后期試驗成本，縮短設計開發時間。

2) 通過參數設計獲得的Pareto解集，驗證了不用大幅增加質量，僅通過參數優化，就能夠達到很好的防護效果。

3) 通過結構優化，可獲得某車型最優防護性能的V型防雷組件的結構型式，最佳V型角度為114°以及最合理的內厚6.89 mm、外底板厚10.96 mm。