前緣鈍度對高速翼型顫振邊界的影響

郭 力,劉杰平, 呂計男,王昕江,季 辰,劉子強

(1.中國航天空氣動力技術研究院, 北京 100074；2. 中國運載火箭技術研究院,北京 100076)

0 引言

為了提高高速飛行器的裝載比例,其結構的剛度與質量下降,從而可能引起結構的氣動彈性振動問題。針對高速飛行器的氣動彈性問題,McNamara等[1]采用NASA Lanley研究中心的CFL3D程序計算了Mach數在2.5～28范圍內高速飛行器的控制面與整機的氣動彈性問題,并與活塞理論進行了對比,分析了活塞理論與CFD/CSD耦合計算的誤差范圍。Lamorte等[2]針對高速飛行器的控制面進行了氣動彈性計算,考察了真實氣體效應、湍流模型、轉捩位置對于顫振邊界的影響,發現上述效應通過影響熱環境,影響氣動彈性性能。Ilie等[3-5]采用大渦模擬(LES)方法,對平板及翼型的氣動彈性響應問題開展了算例研究。季辰等[6]發展了在高超聲速風洞中對結構進行氣動彈性實驗的方法,研究了鈍前緣梯形翼[7]、舵面[8]的氣動彈性特性,并獲得了梯形舵面的顫振邊界。竇怡彬等[9]采用分層求解技術研究了根部固支的高超聲速舵面顫振響應和頻率。葉坤等[10]也采用分層求解技術分析了全動舵面結構的熱邊界影響。

國內外學者對于高超聲速環境下的舵面氣動彈性問題進行了數值、實驗探索,所研究的對象具有工程實際意義,但所研究的外形變化較大,較難形成系統性的認識。在高超聲速條件下,為了減小高超聲速時激波產生的阻力,高速飛行器的舵翼面大多采用尖前緣構型,同時為了降低加熱對結構的影響,需要對前緣進行鈍化。本文以二維翼型為研究對象,通過變化翼型前緣的鈍化程度,探討單純的鈍度因素對翼型氣動彈性性能的影響，為高超聲速下翼型前緣鈍度對顫振特性的影響研究提供參考。

1 計算模型

本文采用二維翼型作為模型考察高速下不同前緣鈍度對顫振邊界的影響。本研究采用了3個不同的前緣鈍度進行了模擬,如圖1所示。第一種為尖前緣構型(圖1(a)),此構型在高速來流條件下會在前緣產生斜激波,激波的強度與正激波相比較小,波后的壓力增加與熱流較小。后兩種分別為1/60m半徑前緣(圖1(b))與1/30m半徑前緣構型(圖1(c))。這兩種構型會在前緣產生較強的正激波,產生的阻力較大。但是此類鈍前緣構型,有利于結構的防熱設計,在氣動加熱效應比較明顯的高速速度范圍能夠較好地保持結構的完整性。

(a)

(b)

(c)圖1 計算采用的翼型截面形狀Fig.1 Illustration of wing sections

計算來流Mach數為5,參考高度為10km。為了得到翼型結構的顫振邊界,通過增加來流密度的方法增加動壓。在高度10km時，Mach為5，來流空氣的動壓為7.6×105Pa,為了得到顫振邊界,又分別考慮了來流動壓為15.1×105Pa、30.2×105Pa、60.5×105Pa這3種工況。通過對這4種情況的考慮,得到了各個來流動壓下的時域響應曲線,并根據這些曲線提取阻尼比,通過插值得到阻尼比為0時的動壓即為顫振邊界。

結構模型如圖2所示。翼型結構為剛體,具有沉浮與俯仰兩個自由度。翼型的轉動中心在翼型的中心,質心在轉動中心前0.1m。質量為10kg,轉動慣量為14kg·m2,沉浮剛度為2×105N·m,扭轉剛度為1×106N·m2。在計算過程中,結構與氣動力耦合,在俯仰與沉浮兩個自由度上運動。

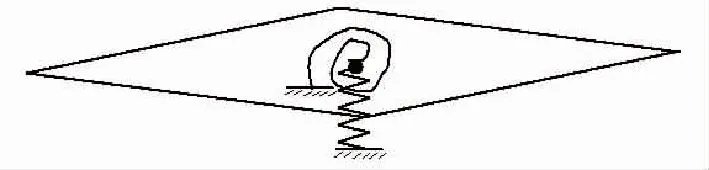
圖2 結構模型示意圖Fig.2 Illustration of structure model

在實際計算過程中,由于考察的是系統的顫振邊界,只需要考慮結構振動的趨勢,從中得到振動的阻尼比,所以結構運動的振幅不需要較大,只需要考慮小振幅就可以。根據此小振幅假設,可以將振動的特征向量進行線性化,得到線性的振動幅度,從而對轉軸的轉動位移進行線性組合運算。翼型的質心在15%弦長處,翼型質量與轉動慣量均設為1,由此得到翼型的沉浮與俯仰兩階模態的頻率分別為ω1和ω2，如表1所示。

表1 兩階模態的固有頻率

2 數值方法

為了方便描述動網格上的流體運動,流場采用積分形式的任意拉格朗日-歐拉(ALE)N-S方程[11]描述,其表達式如下

(1)

(2)

(3)

式(1)～式(3)中，ρ為密度，vi為各個方向的速度，vm,j為各個方向的控制體表面速度，p為壓力，E為總能量，T為溫度。計算過程中空間離散采用Roe格式,時間推進采用雙時間步的LU-SGS方法。

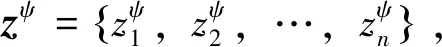
z=ψzψ

(4)

模態坐標的方程為

(5)

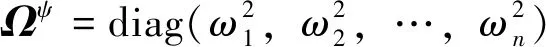
3 顫振分析結果

3.1 流場分析

在Mach數為5.0時,各個構型的流場如圖3所示。對于尖前緣的翼型,在翼型周圍形成了斜激波,激波的傾角由尖前緣的前緣角決定。對于鈍前緣的兩個截面,在前緣前方形成了弓形激波。前緣鈍度的增加,使得前面的弓形激波強度增加,并且后面的斜激波的傾角增加。

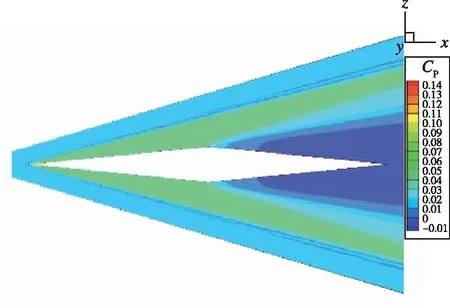
(a)

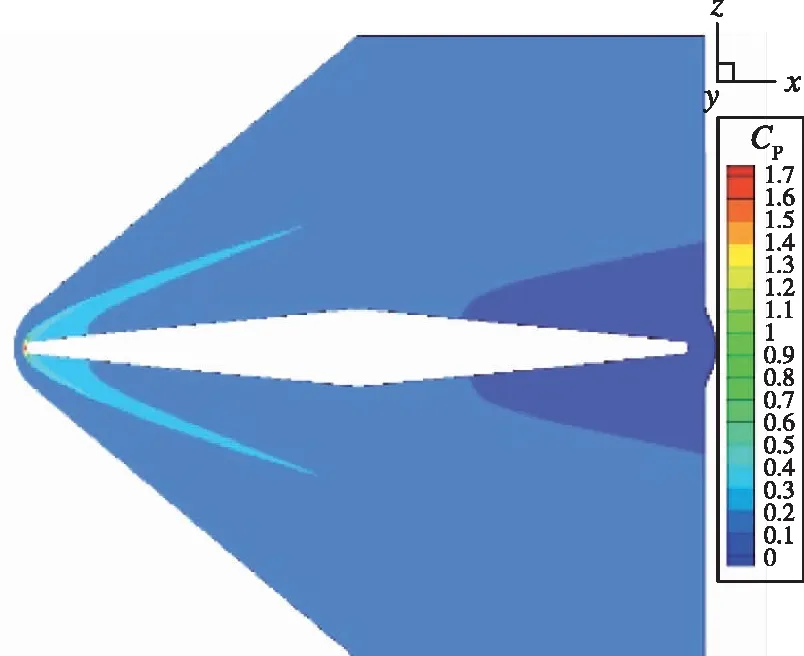
(b)

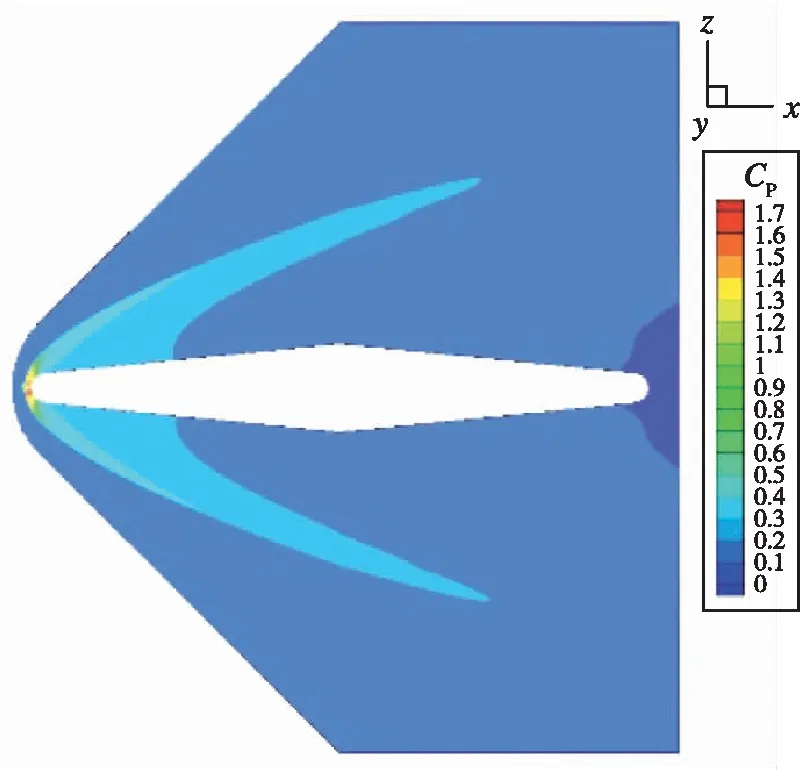
(c)圖3 不同翼型截面與對應的定常流場Fig.3 Flow fields of the 3 wing section shapes

3.2 不同來流動壓下的時域數據

計算初始時刻對翼型施加初始速度擾動,通過計算得到其時域響應數據,對得到的時域數據進行分析可以得到系統的阻尼比和特征頻率。

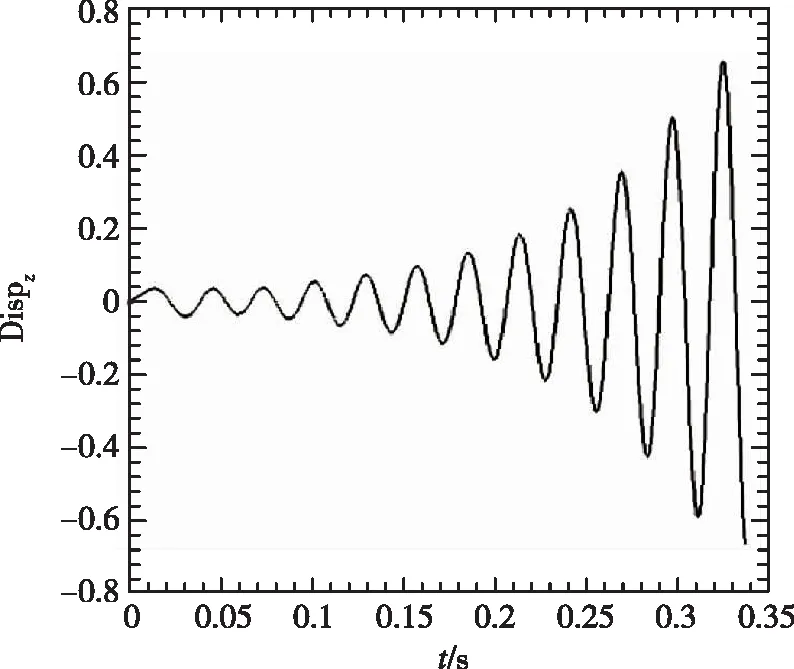
(1) 尖前緣外形變動壓得到的時域數據

從圖4中看到,隨著動壓的增加,振動幅度增大,并最終發散。

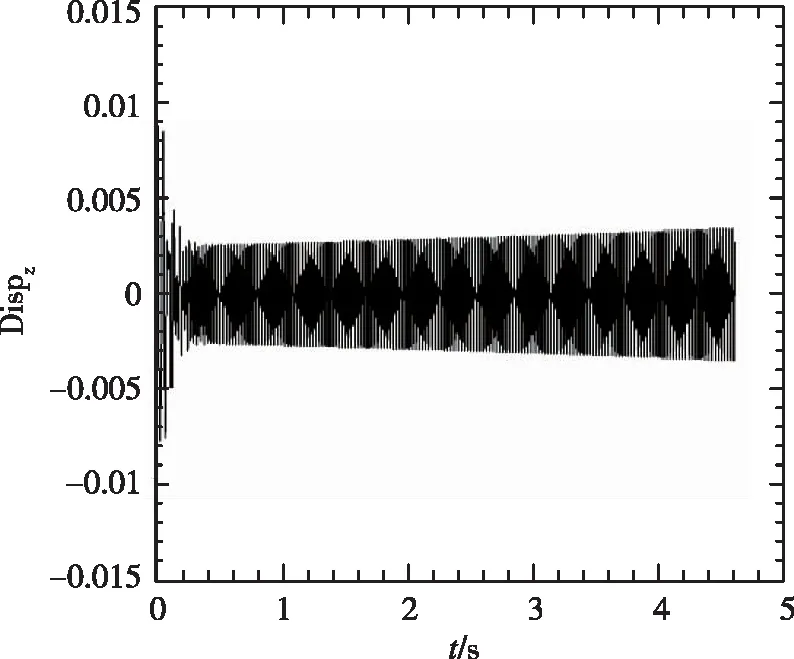
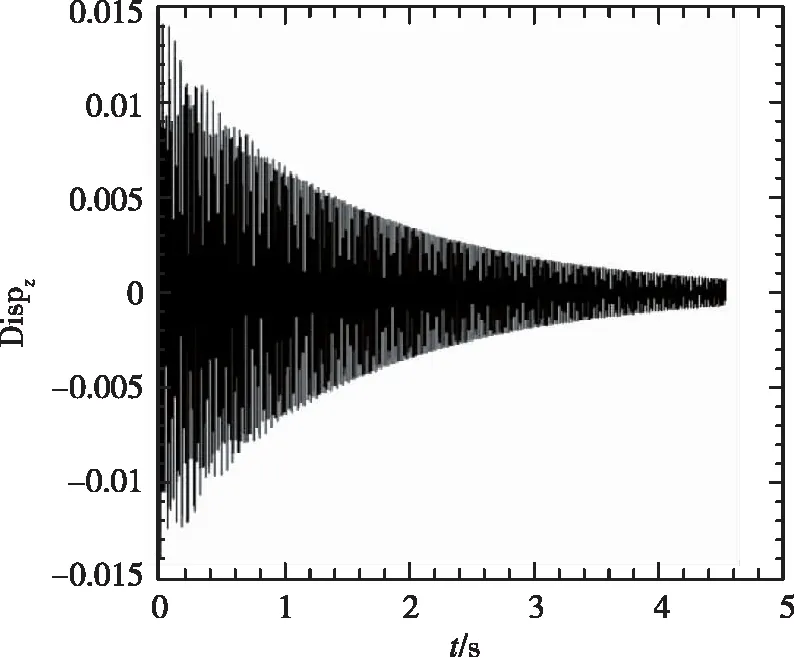
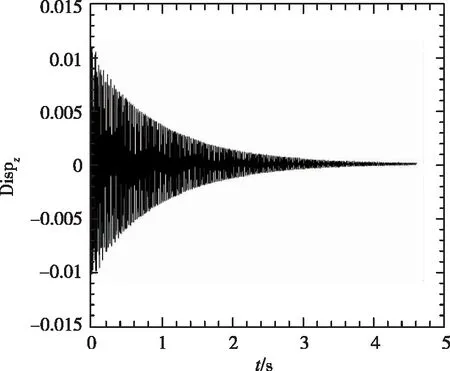
(2) 1/60m半徑前緣外形變動壓得到的時域數據

從圖5中看到,隨著動壓的增加,振動幅度增大,并最終發散。1/60m半徑前緣的時域數據與尖前緣的時域數據相比,從定性角度看到發散較慢。

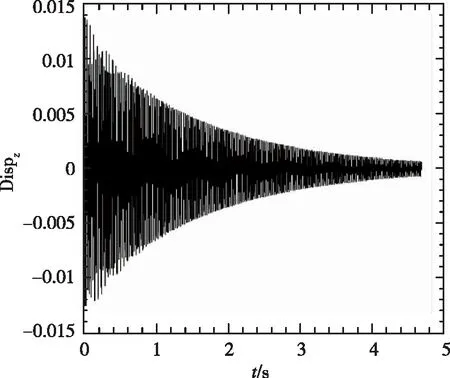
(a)

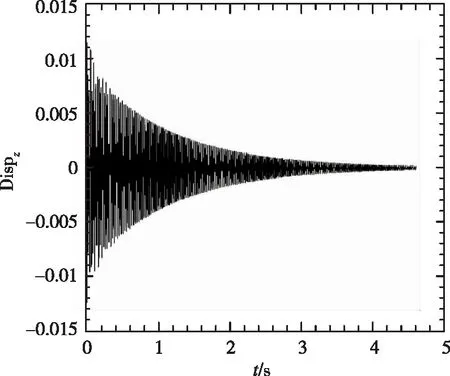
(b)

(c)

(d)

(a)

(b)

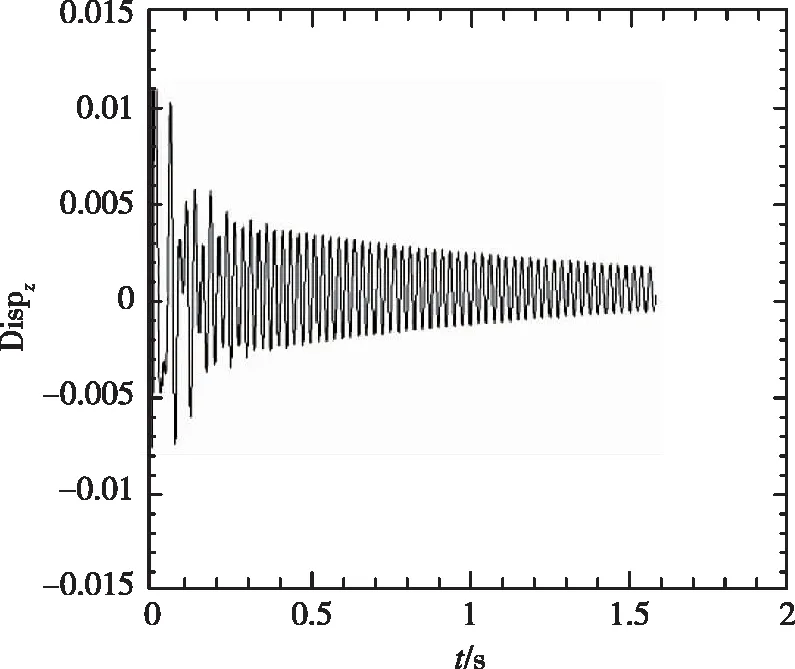
(c)

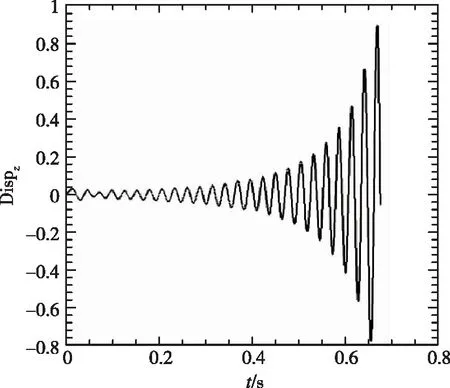
(d)

(3) 1/30m半徑前緣外形變動壓得到的時域數據

通過對上面兩組計算從定性角度觀察,即使對于相同的動壓增長趨勢,1/60m半徑前緣與尖前緣相比發散趨勢減小。反映到計算顫振邊界上,可以預計,前緣鈍度的增加會使得顫振邊界增加。為了進一步確認此趨勢,更進一步增加了前緣的鈍度,采用圖1(c)中的翼型進行了顫振計算。計算采用的Mach數與動壓增加梯度與前面兩組計算相同，并通過固定在翼型前緣的點的位移得到了時域數據。

1/30m半徑前緣的計算的時域數據如圖6所示,與尖前緣與1/60m半徑前緣的計算相比,從定性上看,隨著動壓的增加,發散的趨勢更加不明顯,同時在最大動壓點時域數據未顯示出發散的趨勢,而是呈現出等幅振動的趨勢。

3.3 顫振頻率與阻尼比分析

3.3.1 銳前緣翼型

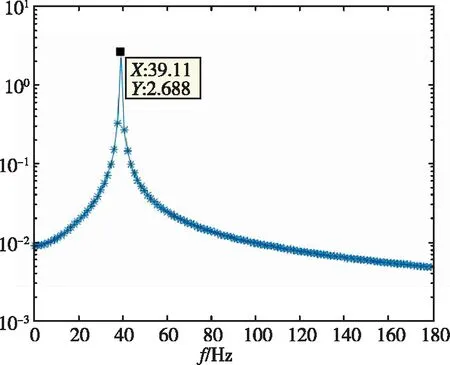
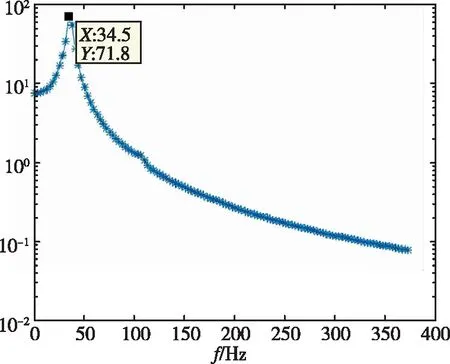
采用自回歸移動平均方法[13](ARMA)對銳前緣翼型前緣的位移時域數據進行了分析,分別得到了不同動壓下的頻率與阻尼比,如表2所示。時域分析得到的頻譜圖如圖7所示。從頻率上可以看出,隨著動壓的增加,最高頻率與最低頻率逐漸靠近。在顫振沒有發生時,時域數據的頻譜分析具有兩個峰值,分別對應兩個模態的振動頻率。當顫振發生時,時域數據發散,此時只有一個對應的頻率。

將來流動壓表示為阻尼比的函數,則在阻尼比為0時對應的動壓為顫振動壓。阻尼比與顫振動壓的函數關系通過已知的動壓-阻尼比數據插值得到。相應的插值曲線與數據點如圖8所示。根據此函數關系,得到阻尼比為0時對應的顫振動壓為3.01×106Pa。

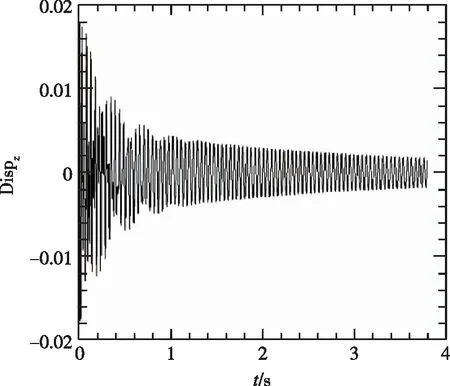
(a)

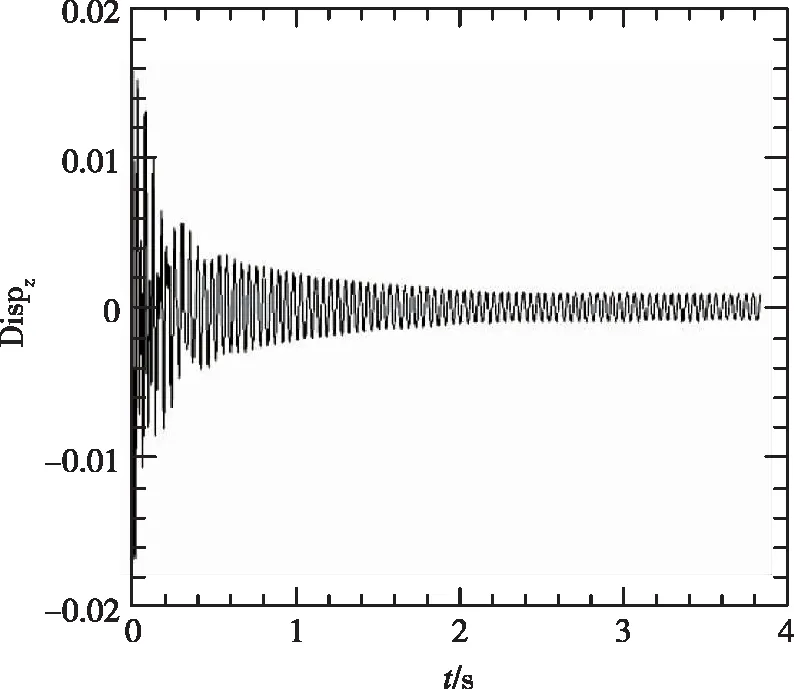
(b)

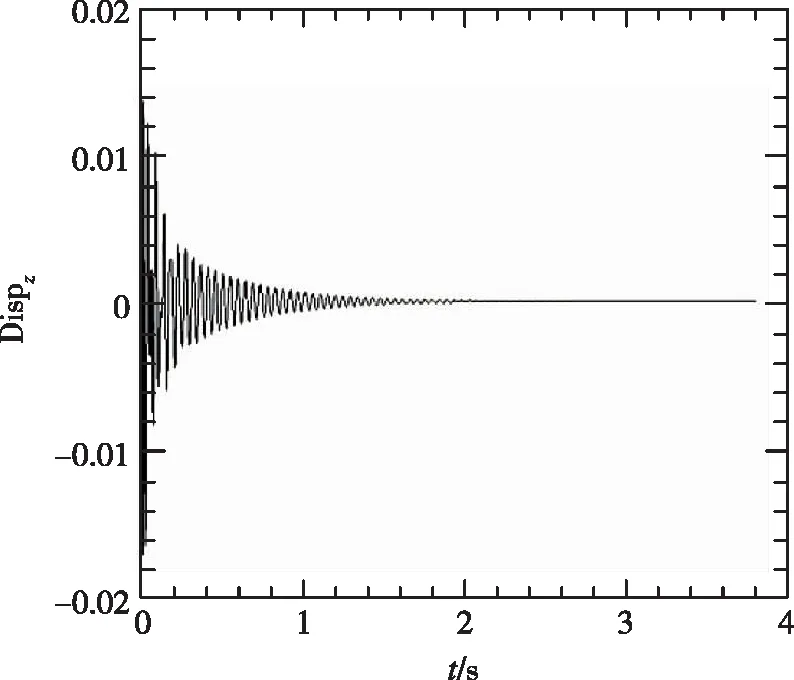
(c)

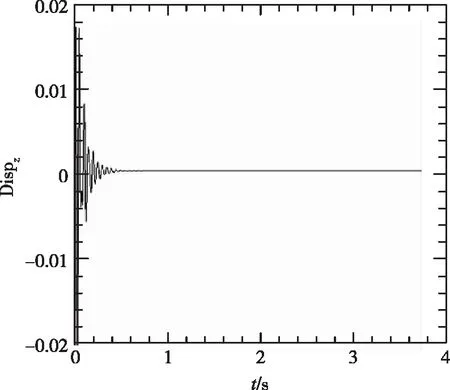
(d)

表2 銳前緣翼型頻率與阻尼比

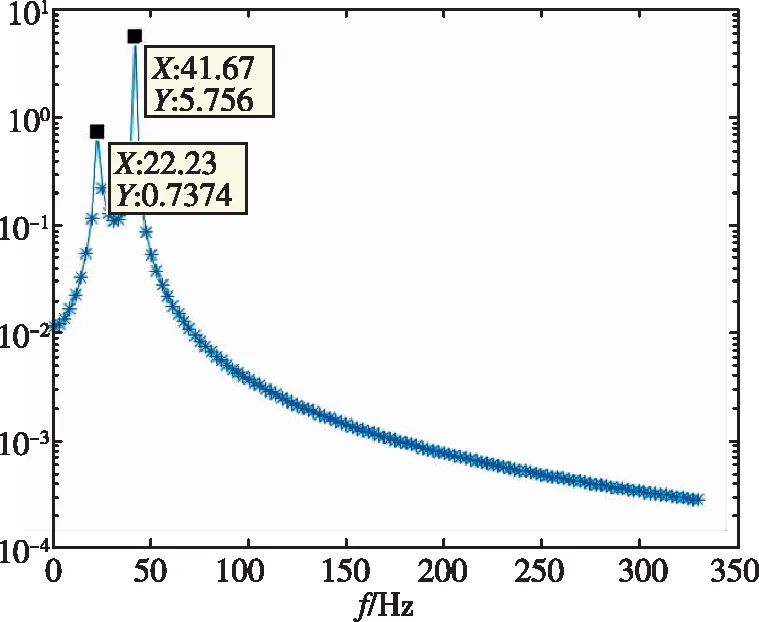
(a)

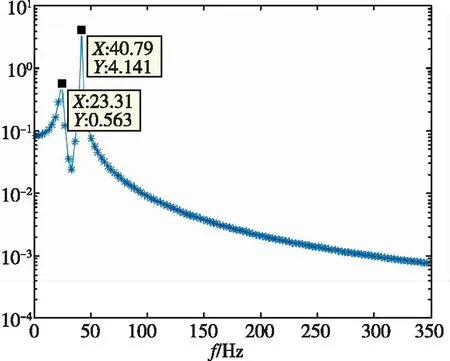
(b)

(c)

(d)

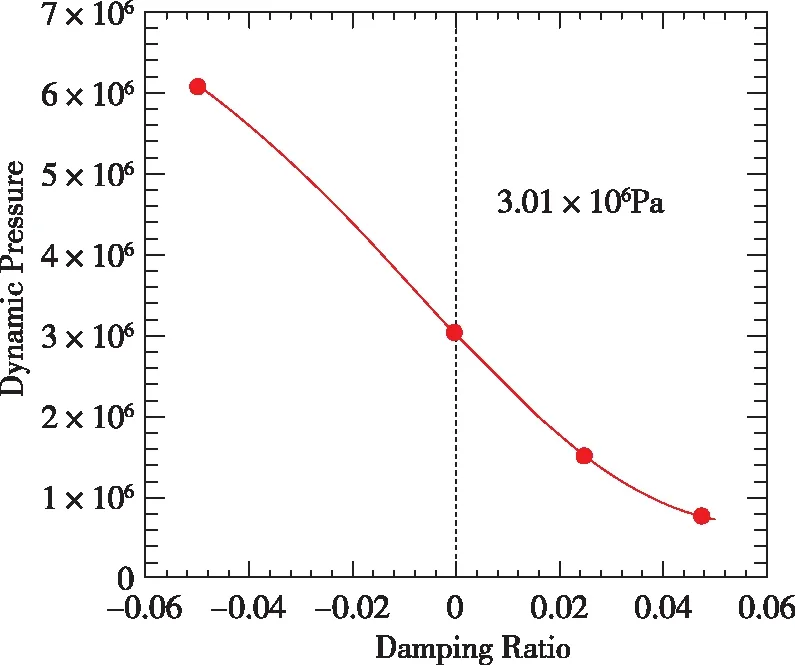
圖8 銳前緣翼型阻尼比與顫振動壓Fig.8 Sharp-edge wing damping ratio vs. incoming flow dynamic pressure

3.3.2 1/60m半徑前緣翼型

對1/60m半徑前緣翼型前緣的位移時域數據進行分析,分別得到了不同動壓下的頻率與阻尼比,如表3所示。時域分析得到的頻譜圖如圖9所示。從頻率上可以看出,隨著動壓的增加,最高頻率與最低頻率逐漸靠近。在顫振沒有發生時,時域數據的頻譜分析具有兩個峰值,分別對應兩個模態的振動頻率。當顫振發生時,時域數據發散,此時只有一個對應的頻率。

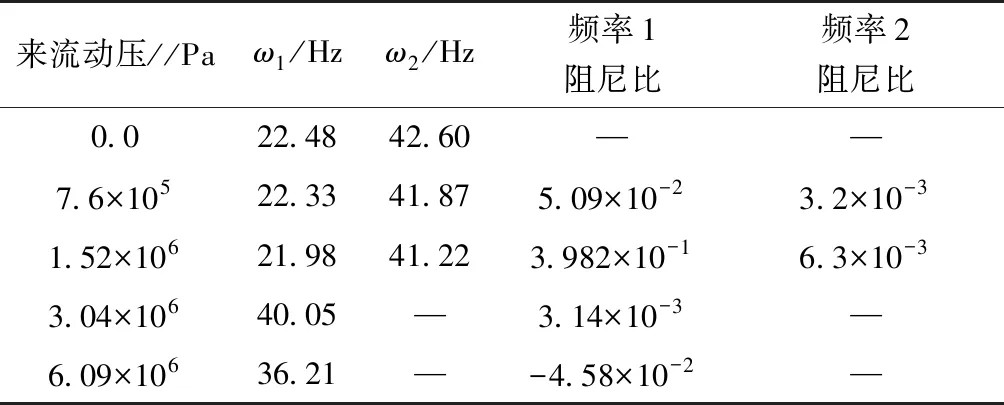
表3 1/60m半徑前緣翼型頻率與阻尼比

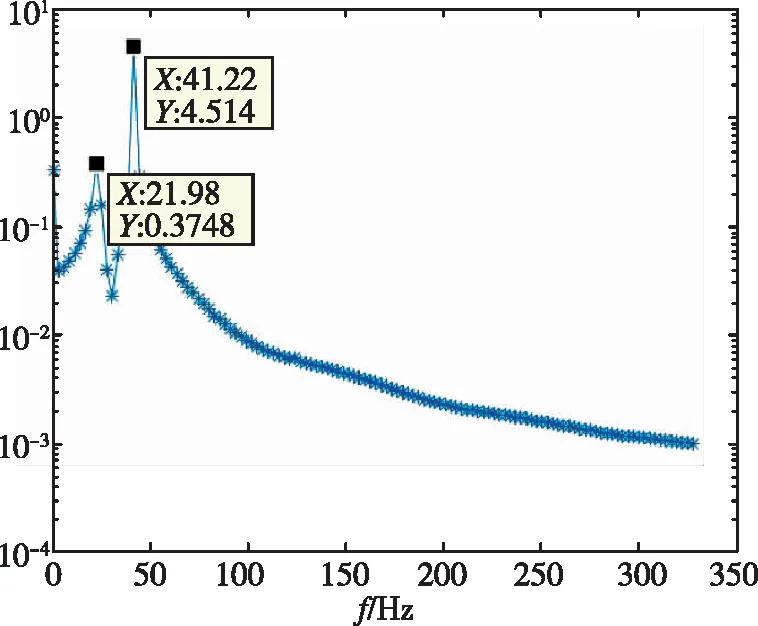
(b)

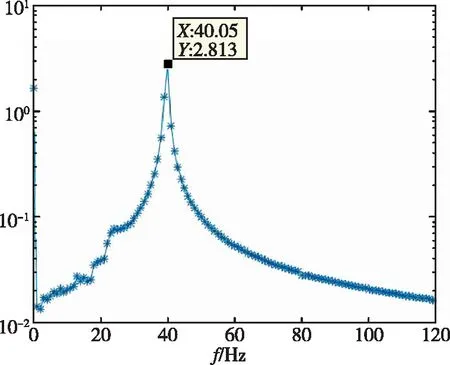
(c)

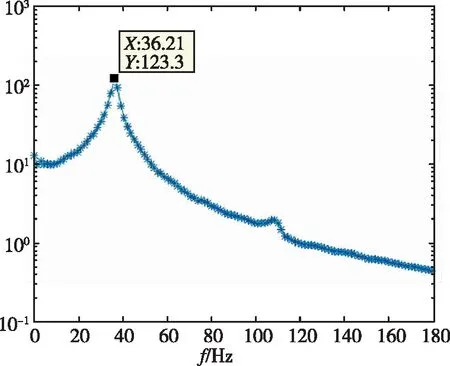
(d)圖9 1/60m半徑前緣翼型頻率分析Fig.9 Frequency of 1/60m blunted-edge wing

將來流動壓表示為阻尼比的函數,則在阻尼比為0時對應的動壓為顫振動壓。阻尼比與顫振動壓的函數關系通過已知的動壓-阻尼比數據插值得到,相應的插值曲線與數據點如圖10所示。根據此函數關系,得到阻尼比為0時對應的顫振動壓為3.25×106Pa。

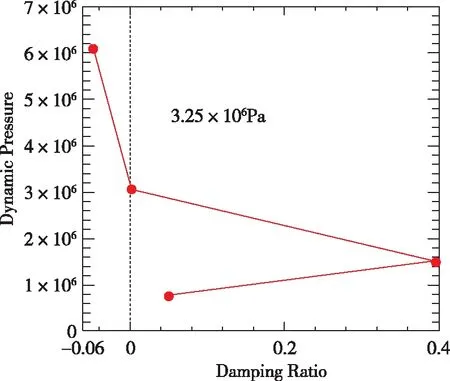
圖10 1/60m半徑前緣翼型阻尼比與顫振動壓Fig.10 1/60m blunted-edge damping ratio vs. incoming flow dynamic pressure

3.3.3 1/30m半徑前緣翼型

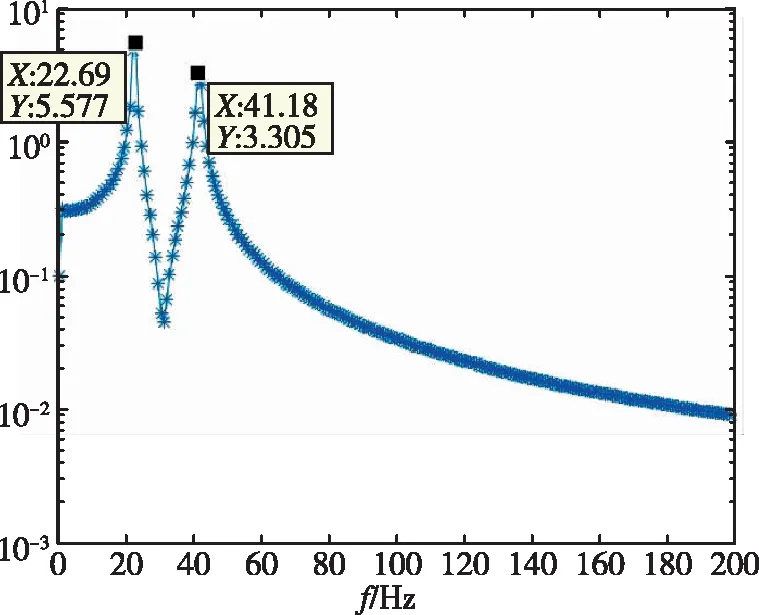
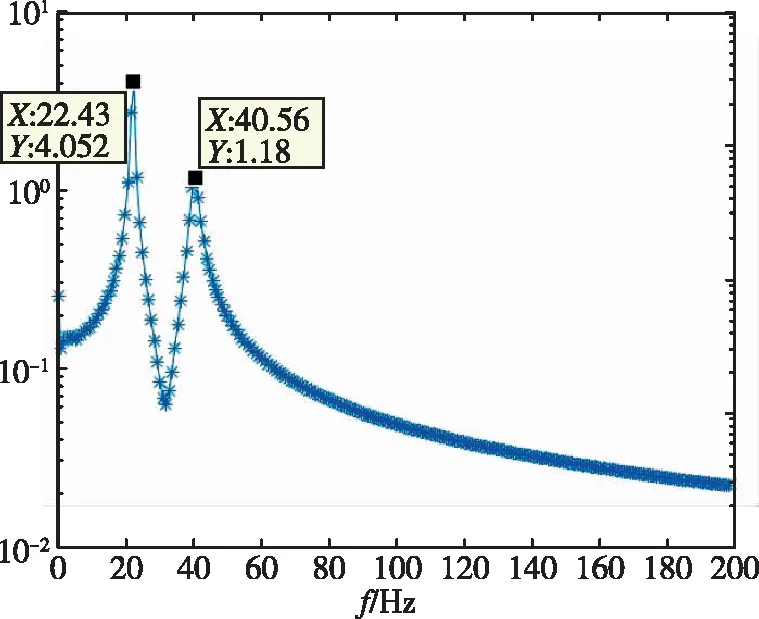
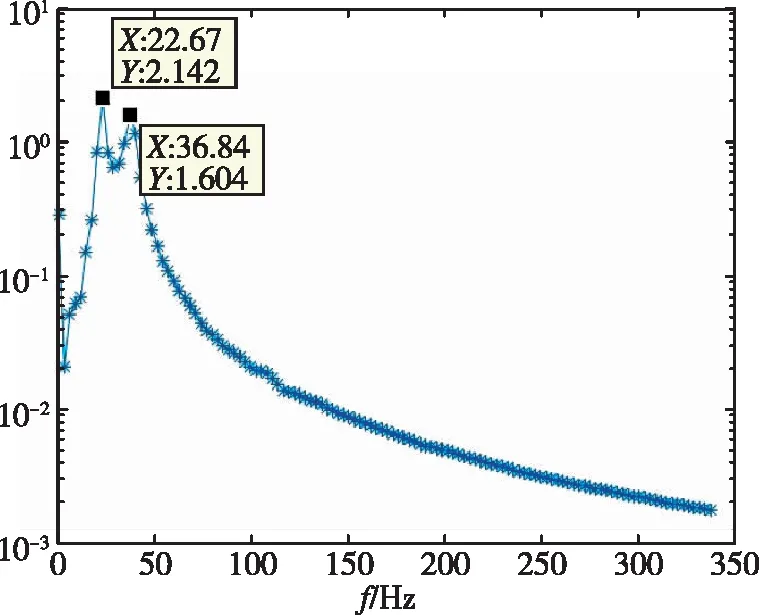
同樣對1/30m半徑前緣翼型前緣的位移時域數據進行了分析,分別得到了不同動壓下的頻率與阻尼比,如表4所示。時域分析得到的頻譜圖如圖11所示。從頻率上可以看出,隨著動壓的增加,最高頻率與最低頻率逐漸靠近。在顫振沒有發生時,時域數據的頻譜分析具有兩個峰值,分別對應兩個模態的振動頻率。與銳前緣和1/60m半徑前緣算例不同的是,1/30m半徑前緣即使在8倍動壓的情況下仍沒有發散。

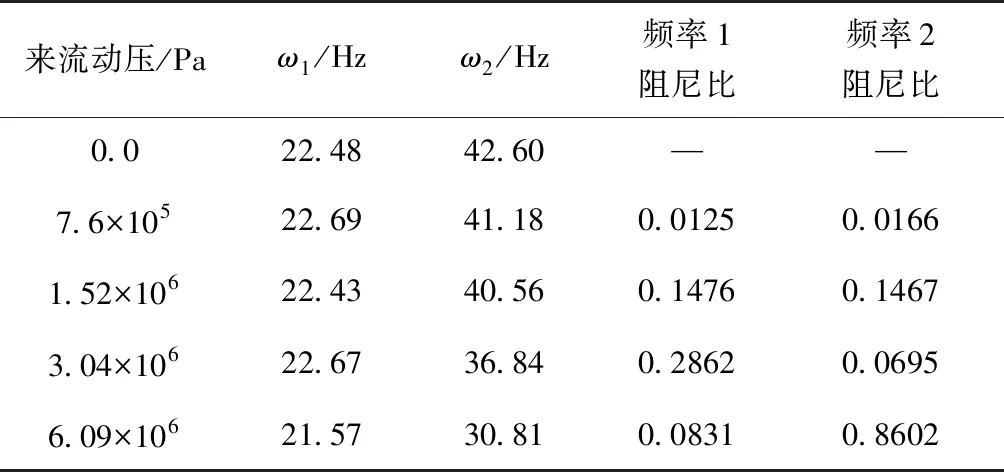
表4 1/30m半徑前緣翼型頻率與阻尼比

將來流動壓表示為阻尼比的函數,相應的數據點如圖12所示。可以看出,即使在最大動壓狀態下,振動仍沒有發散,因此1/30m半徑前緣的翼型顫振邊界高于前面兩種構型。雖然在計算設置的動壓情況下沒有得到結構振動發散,從而沒有得到具體的顫振邊界數據,但是此結果與前面結果的趨勢一致,說明了隨著翼型前緣鈍度的增加,顫振邊界逐漸提高。

(a)

(b)

(c)

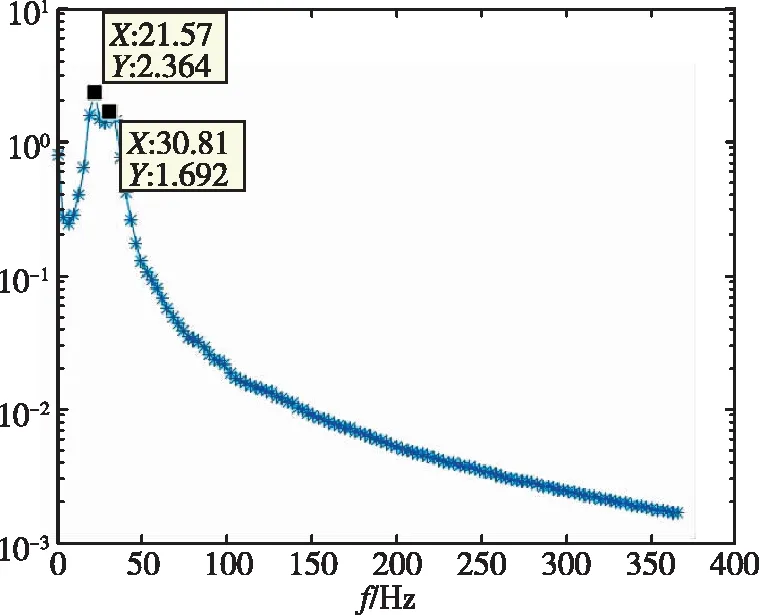
(d)圖11 1/30m半徑前緣翼型頻率分析Fig.11 Frequency of 1/30m blunted-edge wing

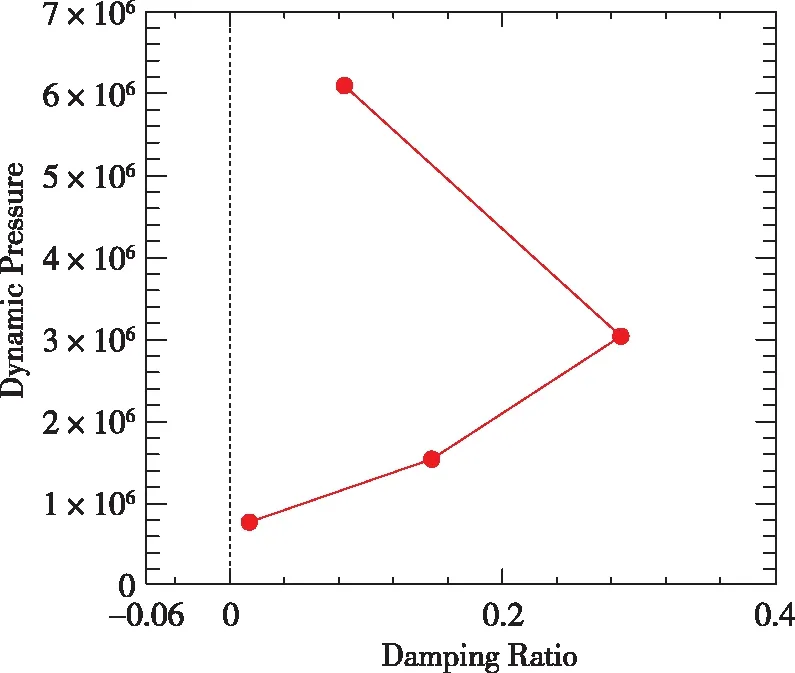
圖12 1/30m半徑前緣翼型阻尼比與顫振動壓Fig.12 1/30m blunted-edge damping ratio vs. incoming flow dynamic pressure

4 結論

根據從銳前緣到1/30m半徑前緣的氣動彈性分析,發現隨著前緣鈍度的增加,即使翼型的剛度、質量不發生改變,顫振邊界也會不斷提高。隨著翼型前緣鈍度的增加,在高速下,頭部激波結構從斜激波轉變為脫體的弓形激波。激波結構的變化使得翼型在運動情況下產生的使得翼型發生俯仰運動的力矩發生了變化。而只有翼型在平動過程中產生力矩并與沉浮運動耦合,才會出現翼型結構的自激振動,從而發散出現顫振現象。在銳前緣情況下,力矩較大,隨著前緣鈍度的增加,翼型上受到的力矩逐漸減小。一個極端的情況為球形,此時如果忽略黏性作用,球形受到的力矩為0。因此,增大前緣鈍度可以提高顫振邊界。