基于追逃博弈的非合作目標接近控制

柴 源，羅建軍，王明明，韓 楠

(1. 西北工業大學航天飛行動力學技術重點實驗室, 西安 710072；2. 西北工業大學青島研究院,青島 266200)

0 引言

空間自主交會是航天領域的一大研究熱點。隨著航天技術的不斷進步，合作目標的自主交會技術已經比較成熟，并成功應用于空間站、在軌服務等多種空間任務中。目前，空間非合作目標如故障衛星、空間垃圾等的自主接近引起了學者的廣泛關注[1]。

非合作目標由于其非合作性，具有如下特征：信息層面不溝通、機動行為不配合、先驗知識不完備等。因此在設計追蹤航天器的軌道控制方法時需要綜合考慮接近過程中的不確定性。針對非合作目標接近問題，目前已經開展了部分研究工作。根據建模方法的不同可將已有研究分為3種：基于視線坐標系的建模與控制、基于目標軌道坐標系的建模與控制、基于追蹤航天器軌道坐標系的建模與控制。在目標軌道坐標系下，王洪宇等[2]提出了一種全局魯棒最優滑模控制器來克服非合作目標所帶來的不確定性。但是由于目標航天器的軌道半徑和速度無法直接得到，基于目標坐標系的建模具有局限性。在基于視線坐標系的建模與控制方面，陳統等[3]建立了姿軌聯合運動模型，并結合具有魯棒性的模糊控制理論實現對非合作目標的接近；殷澤陽等[4]提出了低復雜度預設性能控制方法，實現在未知系統參數情況下的快速高精度目標接近，但是基于視線坐標系的建模為非線性模型，增加了控制求解難度。在追蹤航天器軌道坐標系下，盧山等[5]設計了針對自主交會和攔截兩種接近模式的基于李雅普諾夫的控制律；郭永等[6]基于人工勢場法與蔓葉線理論的障礙物模型，提出了可以避障的滑模控制器。該坐標系下，追蹤航天器可以基于自身的軌道信息及星載傳感器測量得到相對位置和速度信息等進行控制器設計，更加方便簡潔。因此，本文采用基于追蹤航天器軌道坐標系的相對運動模型，以便于控制律的設計。

根據上述分析，多數設計方法都是通過提高控制器的魯棒性來克服非合作目標的機動以及外界干擾等。但是由于非合作目標機動上界的不確定，控制器的設計存在保守性，不利于燃料的優化和接近精度的提高。

博弈論研究的是多個參與者的最優控制與決策問題，其中每一位參與者通過各自目標函數的優化獲得控制策略[7]。近年來，博弈控制方法在各種工程問題的研究中也得到了應用。Abouheaf等[8]、Lin[9]和Mylvaganam等[10]將博弈控制方法應用到多智能體一致性、編隊和避障等問題中。韓楠等[11]利用微分博弈實現了多顆微小衛星對失效航天器的姿態接管控制。Innocenti等[12]利用基于狀態相關里卡提方程SDRE的非合作微分博弈控制實現交會任務。追逃博弈研究追捕者與逃逸者以不同的策略完成追捕任務的協調過程[13]。Bardhan等[14]基于追逃博弈設計了導彈攔截導引律，Li等[15]將近圓軌道上的兩個航天器追逃問題轉化為兩點邊值優化問題進行求解。因此，本文將非合作目標視為理性的博弈參與者，設計追蹤航天器的追逃博弈控制方法，從而實現非合作目標的精確接近。為了簡化納什均衡的求解，追逃博弈模型選擇線性二次型微分博弈模型[16],以得到控制策略的顯式表達式，便于在線應用。

本文介紹了追蹤航天器的追逃博弈控制器的設計思路，基于追蹤航天器和非合作目標的軌道相對運動模型，設計了與相對距離和燃耗有關的目標函數，并建立了二者的追逃博弈模型，推導了追逃博弈的均衡策略，并給出了策略求解算法，通過數值仿真驗證了非合作目標接近的追逃博弈控制方法的有效性。

1 設計思路

本文面向非合作目標接近的軌道控制問題，試圖提出一種基于線性二次型追逃博弈的控制方法。追逃博弈將參與雙方定義為追蹤者和逃脫者，在博弈過程中各博弈方均以己方最大利益為目標，一方的得益必然導致另一方的損失，二者的得失總和為0[14]。將非合作目標接近問題描述為追逃博弈問題，其中追蹤航天器扮演追蹤者，非合作目標扮演逃避者。要接近非合作目標，一方面，追蹤航天器要選擇其控制策略以調節到某種狀態，并盡量減少博弈過程中的燃料消耗。另一方面，理性的非合作目標試圖調節到使追蹤航天器難以追上的狀態，選擇其控制策略的同時將自身燃料消耗降至最低。將二者互相沖突的目標歸納為追逃博弈的目標函數

(1)

式中，X為相對狀態量，具體含義在下文給出。u為追蹤者的控制量，v為逃逸者的控制量。Q>0，Ru>0，Rv>0均為對稱矩陣。追蹤航天器的目標是最小化J，而非合作目標則期望最大化J。

在考慮二者動力學約束的情況下，通過優化二者的目標函數，建立追逃博弈模型：

(2)

通過建立在追蹤航天器上的軌道相對運動方程，將非合作目標軌道接近的任務要求轉化為追逃博弈控制優化問題中的動力學約束。通過最優化問題的求解得到納什均衡控制策略，追蹤航天器盡可能在燃耗最小的情況下實現非合作目標的接近。

2 非合作目標接近的追逃博弈建模

空間非合作目標接近問題涉及兩個近距離航天器間的軌道運動，本節先給出追蹤航天器軌道坐標系下追蹤航天器和非合作目標的相對運動模型，之后建立二者的追逃博弈模型。

2.1 相對運動建模

本文中下標e和p分別代指非合作目標和追蹤航天器。在慣性坐標系下，非合作目標追蹤航天器的軌道運動方程分別為

(3)

式中，rp和re分別為追蹤航天器和非合作目標在慣性坐標系下的位置矢量；up和ue分別為追蹤航天器和非合作目標的控制加速度；μ為地球引力常數，μ=3.986×1014m3/s2。

定義追蹤航天器和非合作目標的相對位置為

r=re-rp

(4)

則慣性坐標系下的相對運動方程為

(5)

將式(5)投影在追蹤航天器本體坐標系中可得

(6)

式中,ωe和ωp分別表示二者的軌道角速度,r表示慣性系下的位置矢量。

在二者相對距離和非合作目標地心距之比足夠小，即r?re的條件下，re=r+rp的2階及高階泰勒展開項可忽略不計，則相對軌道運動方程寫成狀態空間形式

(7)

其中

其中

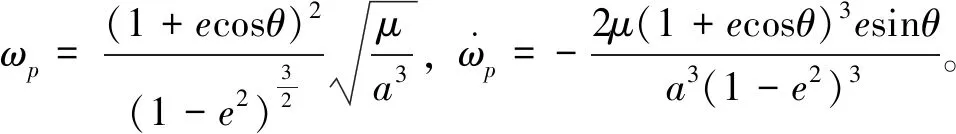
式(7)為非合作目標和追蹤航天器之間的相對運動方程。由于目標航天器為非合作目標，無法得到其軌道信息，因此坐標系建立在追蹤航天器上。追蹤航天器可以基于自身的軌道信息及星載傳感器測量得到相對位置和速度信息，以便進行博弈問題的建模和求解。

2.2 追逃博弈建模

追逃博弈由以下3個要素構成：博弈參與者N={p,e}、各參與者容許策略集Ui、參與者目標函數J[7]。為滿足非合作目標接近的任務要求，設計如下目標函數

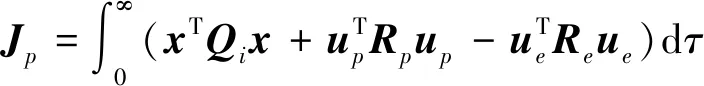
(8)

其中，Q∈R6×6、Rp∈R3×3、Re∈R3×3為對稱正定的加權矩陣。

非合作目標和追蹤航天器進行追逃博弈時，二者通過獨立優化各自目標函數(8)來獲得控制策略。該策略稱為納什均衡，其定義如下：

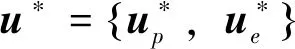
(9)

其中Ui為參與者i的容許控制策略集。

對應于可行控制策略集ui∈Ui的值函數為

(10)

則非合作目標接近的追逃博弈問題可由下式描述

(11)

追蹤航天器通過求解上述優化問題，得到追逃博弈的納什均衡策略，以實現對非合作目標的接近。

3 非合作目標接近的博弈控制策略

本節先給出追逃博弈控制策略的狀態反饋表達式，之后給出李亞普諾夫迭代法進行狀態反饋矩陣的求解。

3.1 追逃博弈控制策略

值函數的微分等價為

(12)

其中，V(0)=0。

定義哈密爾頓函數為

(13)

對應最優值函數的反饋控制策略為

(14)

將其代哈密爾頓函數中可得HJ方程為

(15)

其中，V*(0)=0。

假設最優值函數在狀態x(t)下有線性二次型形式的解

(16)

則追蹤航天器和非合作目標對應的納什均衡反饋控制策略為

(17)

則HJ方程可以整理為

(18)

整理得

(19)

通過對上述代數黎卡提方程(19)進行求解，可以得到對稱正定矩陣P，從而根據式(17)得到狀態反饋控制策略。

本文控制策略與傳統的線性二次型調節器(LQR)方法有相似之處。LQR方法是現代控制理論中較成熟的一種狀態空間設計法，針對線性系統，設計與系統狀態和控制輸入相關的二次型目標函數

(20)

利用動態規劃推導得到代數黎卡提方程

(21)

從而得到狀態反饋的最優控制律

(22)

但是本文的控制策略是基于追逃博弈得到的，考慮最優性的同時，比傳統的LQR控制有更好的魯棒性。

3.2 控制策略求解

代數黎卡提方程(19)的求解已有豐富的研究成果[17]，本文采用李雅普諾夫迭代法進行計算。該方法將代數黎卡提方程解耦為李雅普諾夫方程來獨立運算，算法速度快，準確性高。

迭代算法

(A-SPP(k))TP(k+1)+P(k+1)(A-SPP(k))=
-(Q+P(k+1)SpP(k+1)+P(k+1)SeP(k+1)),
k=0,1,2,…

(23)

初值選擇

0=ATP(0)+P(0)A+Q-P(0)SpP(0)

(24)

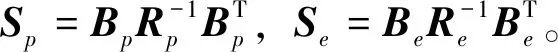
通過迭代求解李亞普諾夫方程式(20)和式(21)可以得到矩陣P。

4 仿真算例及結果分析

為了突出本控制器的優勢，本節將基于追逃博弈的控制方法與傳統LQR控制進行對比，通過3組數值仿真算例驗證基于追逃博弈的控制方法應用于非合作目標接近問題的有效性。假設追蹤航天器初始時刻相對于非合作目標的位置為r=[300,150,-100]Tm，追蹤航天器進行非合作目標逼近，最終二者的相對運動狀態為0。追蹤航天器的控制加速度幅值約束為umax=5m/s2。仿真軌道初始值如表1所示。

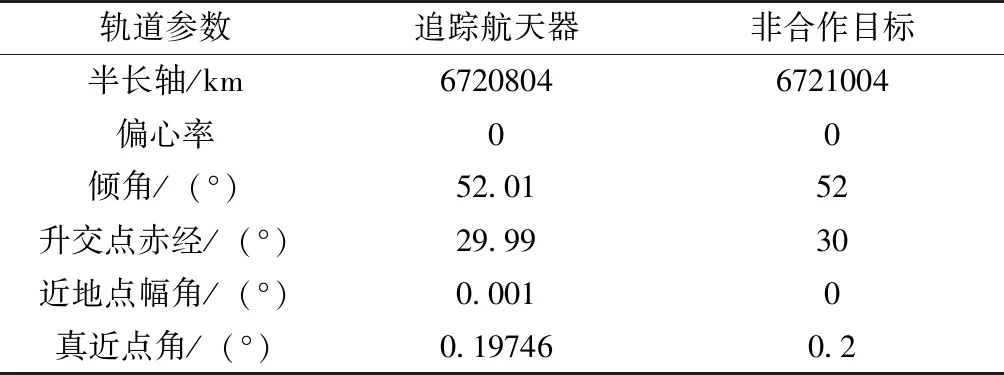
表1 初始軌道參數

算例1假設空間非合作目標不存在機動。該工況相對理想，用于檢驗所提出控制方法的可行性。本文方法選擇權重矩陣為：Q=10-5I6，Rp=0.01I3,Re=0.02I3。LQR方法選擇權重矩陣為：Q=10-5I6，R=0.01I3。仿真時間為200s，仿真步長為0.1s。

圖1和圖3分別為本文提出的方法在接近過程中，非合作目標和追蹤航天器相對距離和相對速度隨時間的變化曲線。圖2和圖4分別為LQR提出的方法在接近過程中，非合作目標和追蹤航天器相對距離和相對速度隨時間的變化曲線。經過約40s，兩種控制器均使追蹤航天器與非合作目標的相對距離穩定在0.5m左右。

圖5和圖6分別為兩種控制器下追蹤航天器的控制加速度隨時間變化曲線。可以看出，在整個非合作目標接近過程中，初始相對距離較遠，接近非合作目標所需控制力較大，隨著相對距離的減小，控制力逐漸減少并趨于0。通過上述分析，在非合作目標無機動的理想情況下，兩種方法均可實現對非合作目標的接近。

算例2假設非合作目標的未知機動為納什均衡策略。該工況下，非合作目標為理性的博弈參與者，有意識地與追蹤航天器對抗。假設非合作目標的最大控制加速度umax=2m/s2。本文方法選擇加權矩陣為：Q=10-5I6，Rp=0.01I3,Re=0.02I3。LQR方法選擇目標函數中的矩陣為：Q=10-5I6，Rp=0.01I3。仿真時間為200s，仿真步長為0.1s。

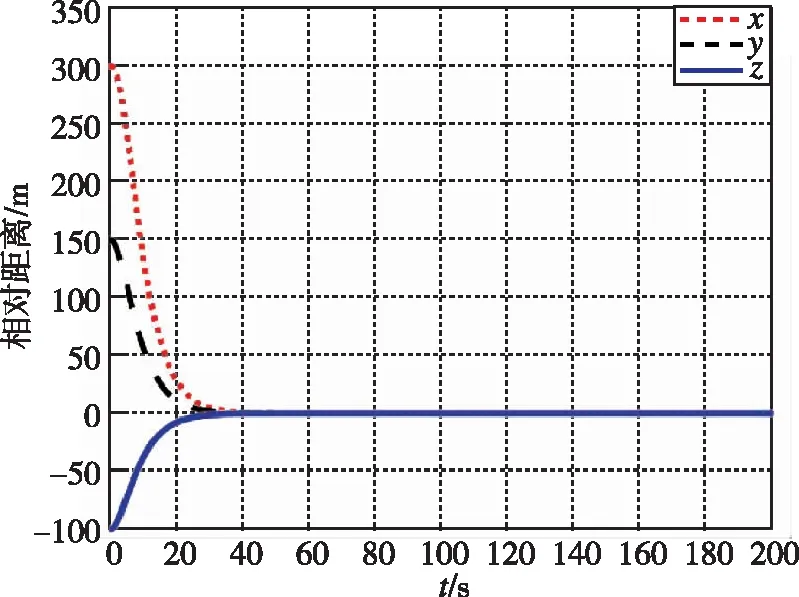
圖1 相對距離隨時間變化曲線(本文)Fig.1 Relative distance by game

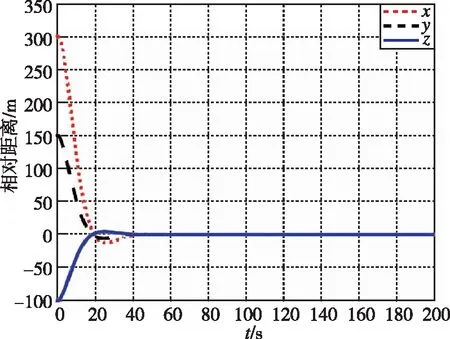
圖2 相對距離隨時間變化曲線(LQR)Fig.2 Relative distance by LQR

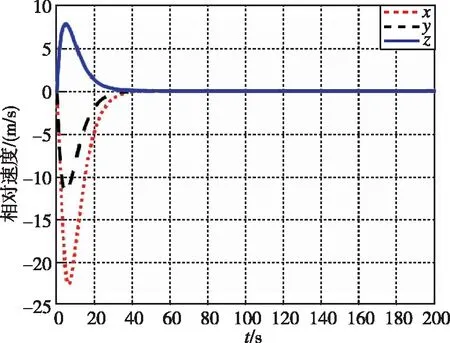
圖3 相對速度隨時間變化曲線(本文)Fig.3 Relative velocity by game

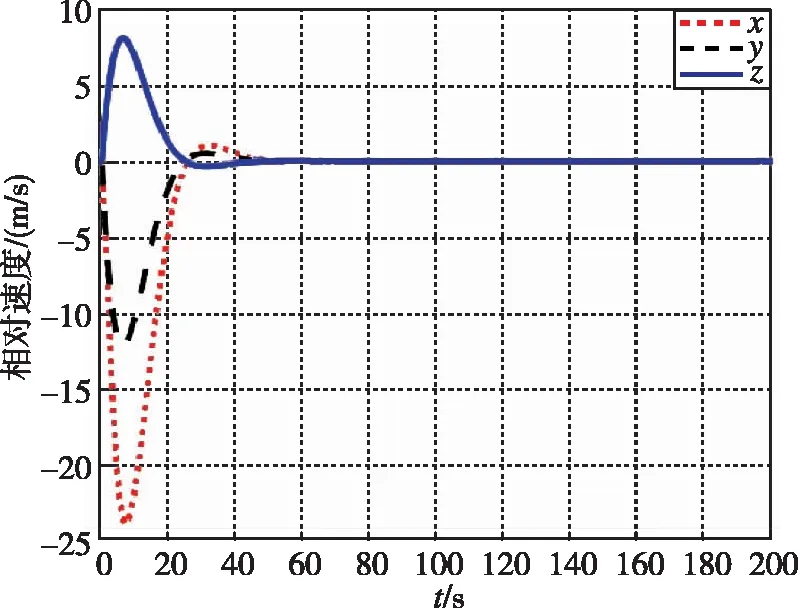
圖4 相對速度隨時間變化曲線(LQR)Fig.4 Relative velocity by LQR

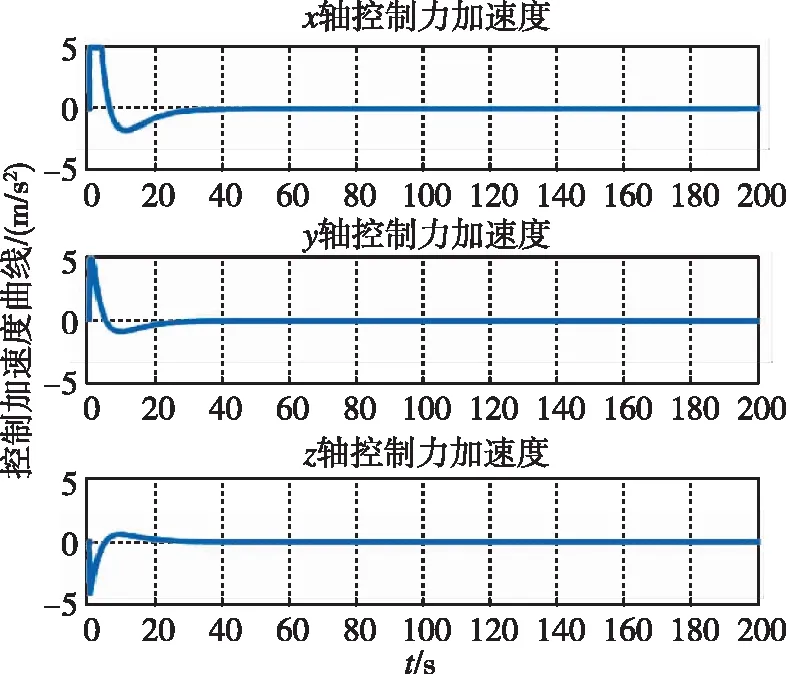
圖5 控制加速度隨時間變化曲線(本文)Fig.5 Control acceleration by game

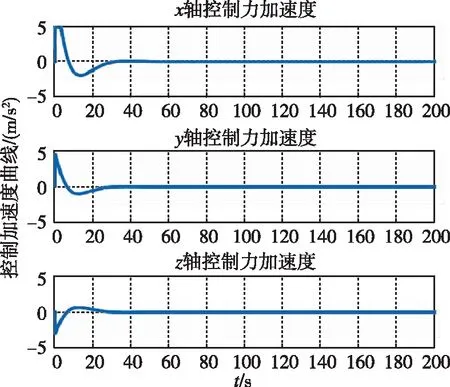
圖6 控制加速度隨時間變化曲線(LQR)Fig.6 Control acceleration by LQR

圖7和圖8為追逃博弈方法與LQR方法分別作用下的相對位置變化圖。圖9和圖10為兩種控制分別作用下的相對速度變化圖。可以看出，在非合作目標采取納什均衡策略時，本文所提出的方法能夠快速平滑地使相對距離收斂到0.5m左右的穩定值。而LQR方法則是震蕩收斂狀態，所需時間較長。

圖11和圖12分別為兩種控制器下追蹤航天器的控制加速度隨時間變化曲線。可以看出，基于追逃博弈的控制方法可以在燃耗較少的情況下快速收斂到0。對比二者的目標函數，在二者都采取納什均衡策略的情況下，即基于追逃博弈的控制下，J*=104；而在LQR控制下，J*=141，由此也可以驗證式(9)的右不等式成立。

算例3假設非合作目標存在未知機動[4]：

本文方法選擇權重矩陣為：Q=10-5I6，Rp=0.01I3,Re=0.008I3。LQR方法選擇權重矩陣為：Q=10-5I6，Rp=0.01I3。仿真時間為200s，仿真步長為0.1s。

在本工況下，圖13和圖14為追逃博弈方法與LQR方法分別作用下的相對位置變化圖。圖15和圖16為兩種控制方法下的相對速度變化圖。可以看出，盡管非合作目標存在未知機動，追逃博弈的控制方法仍可以實現狀態的收斂，精度在1m左右。而LQR方法魯棒性不足，無法實現非合作目標的接近。

圖17和圖18分別為兩種控制器下追蹤航天器的控制加速度隨時間變化曲線。可以看出，控制加速度持續并不為0，而是隨著非合作目標的運動震蕩。

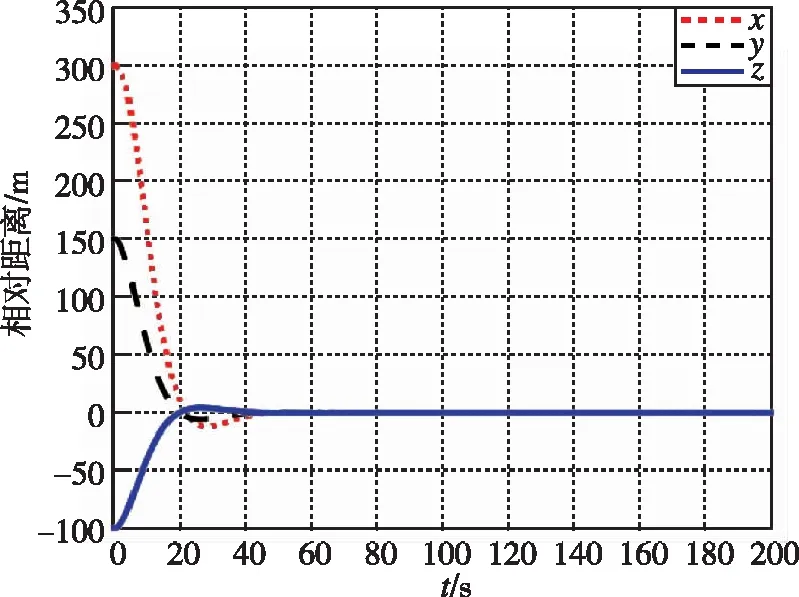
圖7 相對距離隨時間變化曲線(本文)Fig.7 Relative distance by game

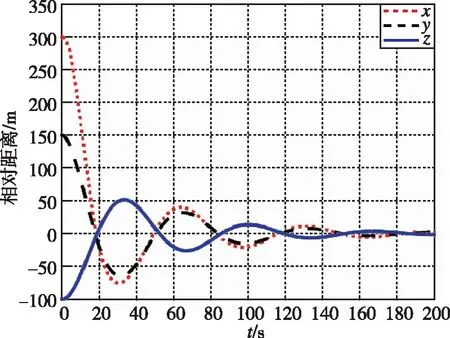
圖8 相對距離隨時間變化曲線(LQR)Fig.8 Relative distance by LQR

圖9 相對速度隨時間變化曲線(本文)Fig.9 Relative velocity by game

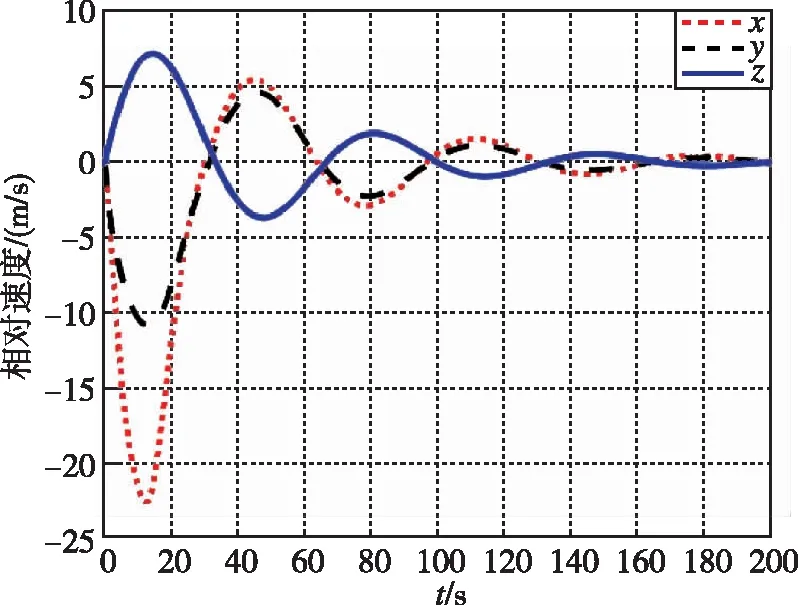
圖10 相對速度隨時間變化曲線(LQR)Fig.10 Relative velocity by LQR

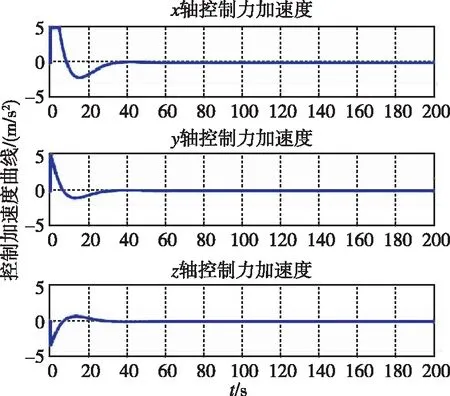
圖11 控制加速度隨時間變化曲線(本文)Fig.11 Control acceleration by game

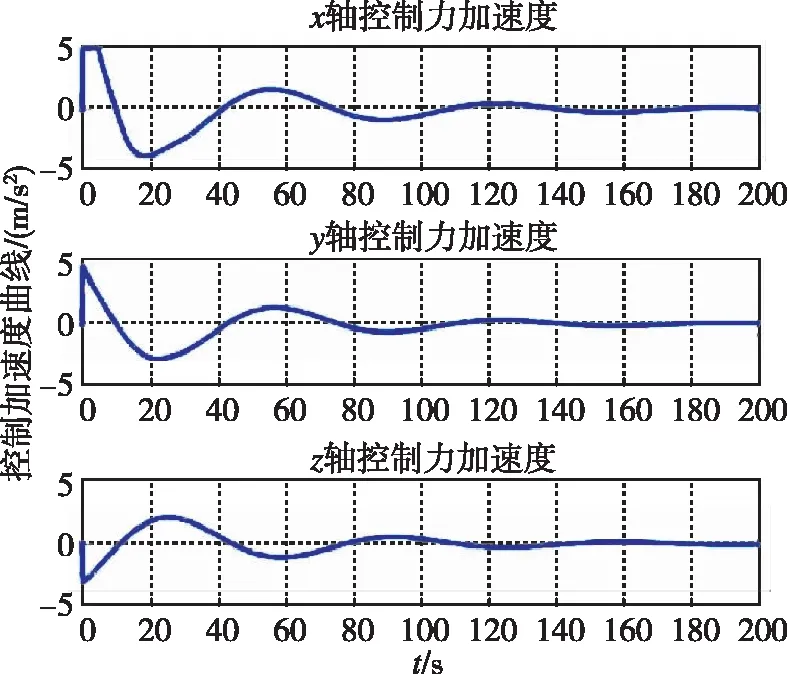
圖12 控制加速度隨時間變化曲線(LQR)Fig.12 Control acceleration by LQR

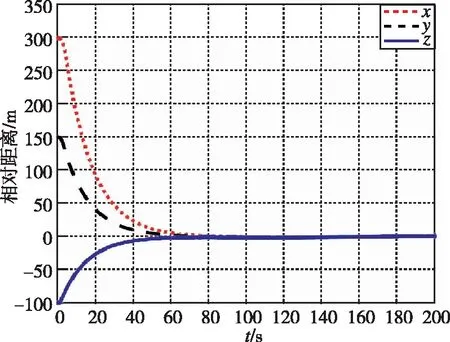
圖13 相對距離隨時間變化曲線(本文)Fig.13 Relative distance by game

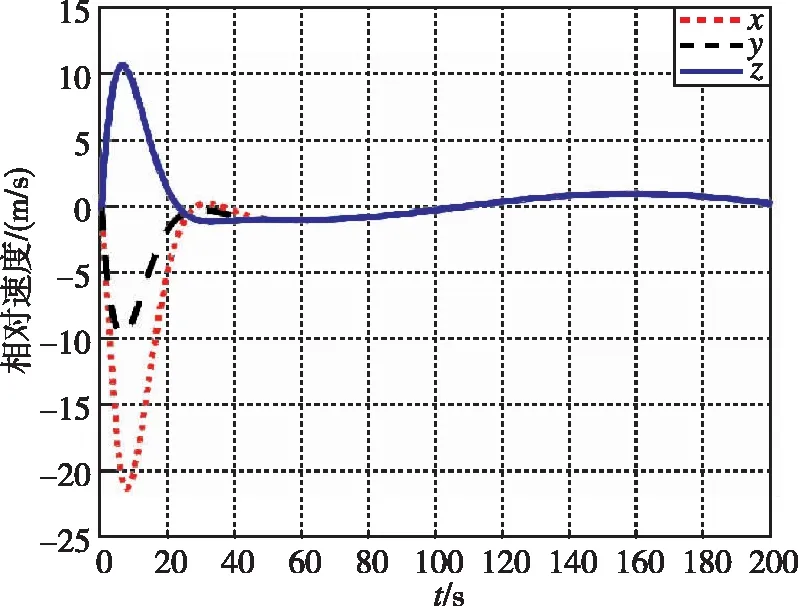
圖14 相對距離隨時間變化曲線(LQR)Fig.14 Relative distance by LQR

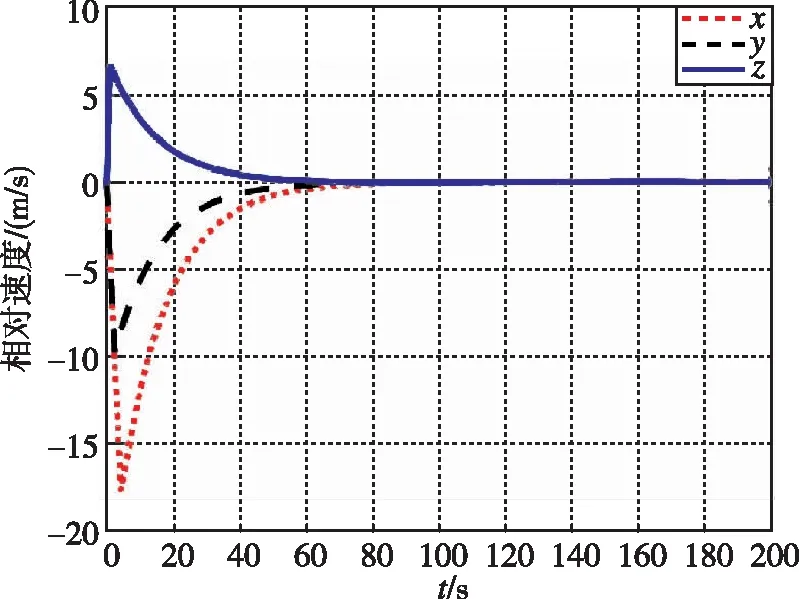
圖15 相對速度隨時間變化曲線(本文)Fig.15 Relative velocity by game

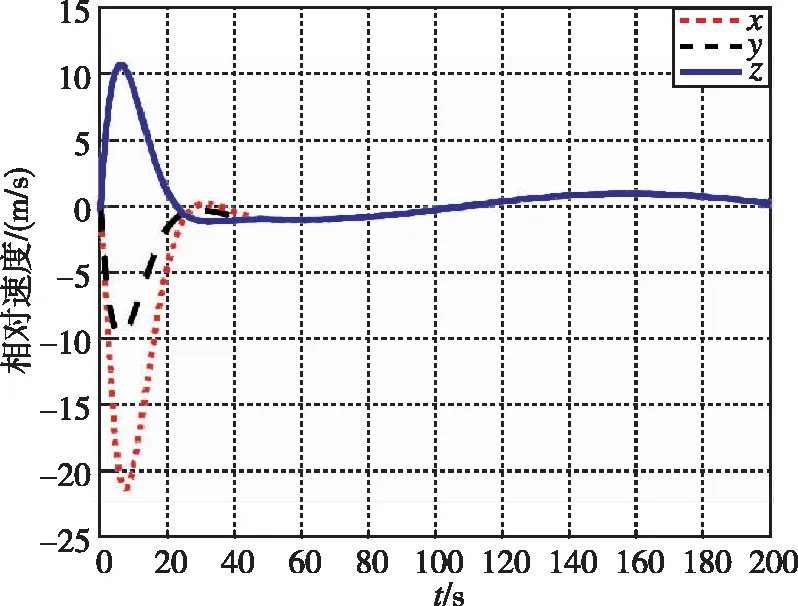
圖16 相對速度隨時間變化曲線(LQR)Fig.16 Relative velocity by LQR

圖17 控制加速度隨時間變化曲線(本文)Fig.17 Control acceleration by game

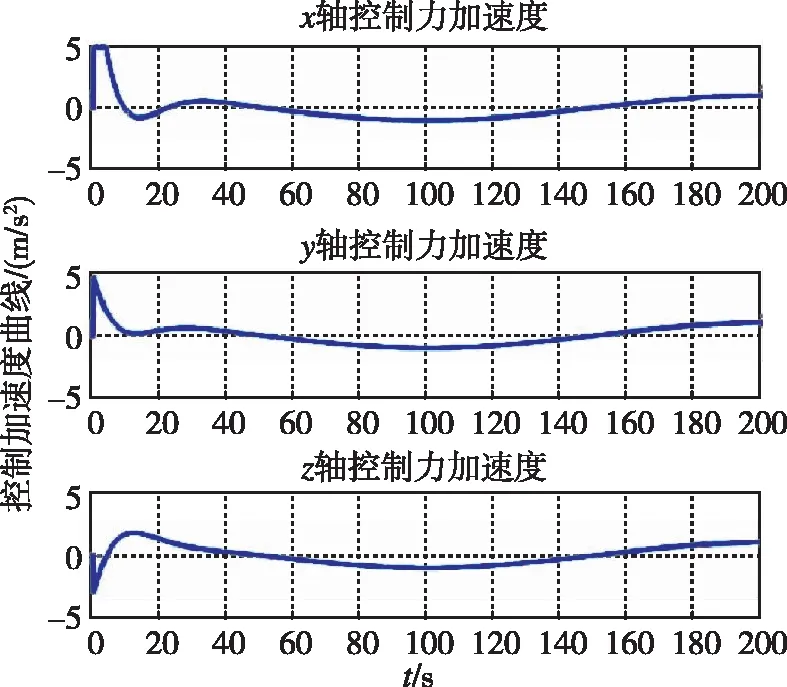
圖18 控制加速度隨時間變化曲線(LQR)Fig.18 Control acceleration by LQR

5 結論

本文針對空間非合作目標的接近控制問題，基于追逃博弈方法設計了追蹤航天器的軌道控制器。面向非合作目標接近的任務要求，合理設計了博弈的目標函數，并結合二者的動力學約束，實現了對非合作目標和追蹤航天器之間追逃博弈的數學描述。結合線性化動力學，通過優化二次型目標函數，得到線性二次型追逃博弈的納什均衡解策略。基于追逃博弈的控制策略具有顯式表達式，方便工程應用。數值仿真驗證了本文設計的追逃博弈控制方法對于存在未知機動的非合作目標的有效性。本文未考慮接近過程中的姿態運動，后續研究將進一步考慮能夠實現非合作目標接近的姿軌聯合博弈控制。