多自由度仿生撲翼飛行機器人結構設計與分析

王 超,屈方杰,黃恒敬,仲 軍

(河海大學機電工程學院,南京 213000)

0 引言

在飛行機器人領域,仿生飛行機器人擁有相較于普遍的四軸飛行器更加美觀的外形,并且能模擬鳥類飛行時的啟動、懸停和降落時的動作。這類仿生飛行器因為外觀與鳥類相似,能更好地在軍事、反恐及娛樂等眾多領域,發(fā)揮偵察、巡邏與教育等積極作用。

早在1973年,Weis-Fogh[1]就針對黃蜂的飛行特性,提出了撲翼飛行的概念,并詳細地分析計算了撲翼產(chǎn)生的升力,為飛行領域開創(chuàng)了新的學科分支。

2015年，Yang等[2]在仿生撲翼飛行器原理的設計與研究中,對撲翼機器人的具體設計步驟做了詳細的介紹。在設計撲動機構的主體時,采用了被普遍使用的撲翼機構,并且在該機構的基礎上加了一個用于模擬鳥類內(nèi)外部肌肉交替收縮的平行機構,并對機構進行UG建模、ADAMS和Fluent的仿真分析,最后對機翼和尾部形狀進行仿生設計。

2015年，潘爾振[3]結合海鷗的功能和性能指標,通過結構設計和樣機選型等過程,設計出具有一個自由度的撲翼機器人,并開發(fā)了一套實驗裝置測試結構合理性等性能指標,最后基于數(shù)據(jù)對結構進行優(yōu)化設計。

2016年，阮龍歡[4]對撲翼飛行機器人的應用背景和技術做了深入的分析和研究,并設計一種類似蜂鳥撲動的撲動-扭轉兩自由度耦合驅(qū)動機構,在ADAMS軟件中建立了基于該機構的虛擬樣機,并分析了虛擬樣機的基本運動特性。

在仿生撲翼飛行器的研究上,國外的研究起步早,技術暫時還領先于國內(nèi)。隨著國內(nèi)各大高校、實驗室以及飛行器愛好者對于撲翼飛行的關注,已經(jīng)有不少學者取得不錯的成績，但研制成功的飛行器大多數(shù)還是單自由度,無法達到真正模仿鳥類飛行和大范圍普及推廣的程度,距離世界領先技術還有不少的差距。歸根結底是因為仿生飛行機器人相較于市面上的普通飛行器,存在設計復雜、控制復雜的問題,并且現(xiàn)有的研究仿生程度不高,運動學和動力學領域?qū)τ趽湟斫Y構的建模分析還有待深入探討和研究,智能控制系統(tǒng)還有待進一步開發(fā)和完善[5-10]。大型撲翼飛行機器人結構研究對于開發(fā)多自由度仿生撲翼飛行器在理論和實際應用上都具有很強的研究價值[11-14]。

本文旨在對大型的撲翼飛行機器人的結構進行研究。由于多自由度仿生撲翼飛行器在飛行時的頻率較低,所以在每次撲動時要求的升力和推動力比螺旋式飛行器大,因此,精妙的撲翼傳動是結構設計中的關鍵問題。在理論的結構設計后,還需要對設計出的結構進行動態(tài)構件計算分析、運動學計算分析、建模仿真等,以提高設計的準確性和可行性。

1 結構設計

1.1 海鷗飛行方式與運動規(guī)律分析

翅膀是海鷗能夠飛行的主要身體部分,輕質(zhì)且堅韌的羽毛和骨骼在撲動的過程中產(chǎn)生飛行所需要的升力。海鷗的羽毛大致分為覆羽和飛羽兩類，如圖1所示。覆羽排列密且短,飛羽排列稀疏但長。海鷗的飛行主要由起飛階段、巡航階段、轉向、降落階段組成。

海鷗在巡航過程中,翅部有4個基本的撲動動作：下行程、折疊過程、上行程、伸展階段。這4個動作可以大致看做一個完整的拍打過程。翅膀在下行程前的伸展階段需要盡可能大地展開,這樣翼展和升力面積才能達到最大值,并在下行程階段產(chǎn)生所需的大部分升力。上行階段是被動回復的過程,并且行程需要的時間很短。在這個階段之前,翅膀折疊,目的是縮短翼展和減少阻力。在上行程中,空氣阻力會急劇增大。如果鳥類能在這個時候折疊翅膀,可以減少有效的作用風區(qū),從而大大減少空氣阻力[15]。

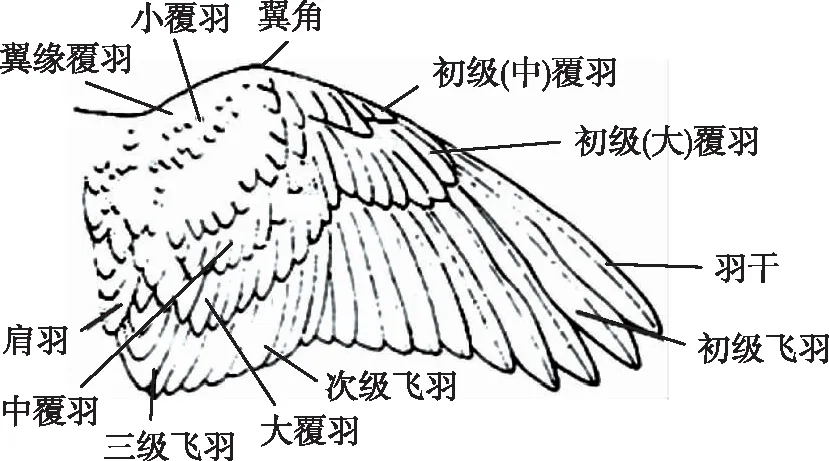
圖1 鳥類翅膀示意圖Fig.1 Schematic diagram of bird wings

海鷗一類的大型鳥類主要撲動飛行的頻率比較低。在巡航過程中,因為翼展大小決定了撲動頻率,海鷗的撲動頻率大約為5Hz,最低的時候只有1Hz～2Hz[16]。

根據(jù)觀察發(fā)現(xiàn),在海鷗的一個拍打過程中,不僅翅部上下?lián)鋭?而且根據(jù)上下形成的空氣阻力不同,翅膀還會有小幅度的接近線性扭轉,翅尖部分扭轉幅度最大,越靠近身體方向扭轉幅度越低。

海鷗在巡航飛行過程時,一對翅膀的運動是完全左右對稱的,這樣的運動有利于海鷗在大型的風浪面前保持身體的平衡和對抗氣流飛行,例如Festo公司研制的一款Smartbird[17]仿生海鷗機器人,其運動典型動作如圖2所示。

圖2 Festo公司Smartbird仿生海鷗Fig.2 Festo’s Smartbird bionic seagull

1.2 仿海鷗撲翼飛行機器人結構設計

1.2.1 整體結構設計

設計的要求是需要滿足仿海鷗飛行特點和產(chǎn)生足夠的升力維持飛行，以及在外形上與海鷗相似。使用SolidWorks軟件設計結構,生成三維模型可以更加直觀地修改和完善結構設計。

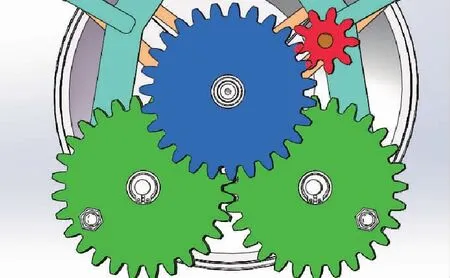
圖3 傳動部件局部圖Fig.3 Partial view of transmission components

圖4 前支骨架零件圖Fig.4 Front support skeleton parts

圖5 螺栓連接剖視圖Fig.5 Sectional view of bolted connections

圖6 最終裝配效果和海鷗對比圖Fig.6 Comparison of final assembly effect and seagull

1.2.2 撲翼結構設計

翅膀翼型骨架的設計上,參考美國NACA系列翼形,選擇了具有較好氣動特性的弧形機翼,再根據(jù)前文所確定的翼展投影面積,設計出的翅膀翼型骨架如圖7所示。鏤空的設計既保證飛行時所需要維持形狀的強度,也減輕了零件的質(zhì)量,同時根據(jù)仿生學和流體力學的研究成果,一邊翅膀有8個翼型骨架,從機身向外到最后一個翼型骨架,每個骨架的形狀和尺寸都略有差異,翼型骨架的前沿的小孔和后沿都將與鋼絲串接在一起,這樣在末端翼型骨架被施加扭力時,其他骨架也會隨之扭動。這樣的設計模擬了海鷗在不同空氣阻力時,翅膀會有小幅度的接近線性扭轉,翅尖部分扭轉幅度最大,向身體方向扭轉幅度遞減。

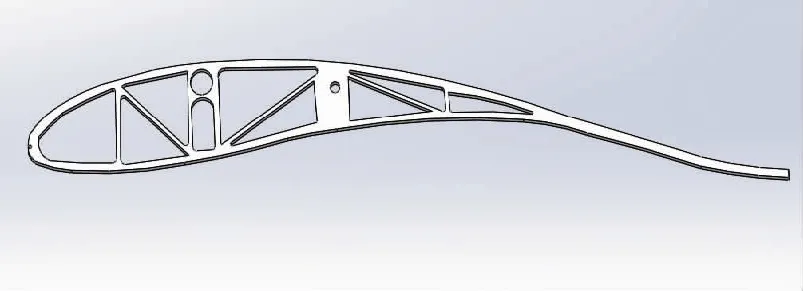
圖7 翅膀翼型骨架Fig.7 Skeleton of wing airfoil

機尾部還加裝了微型舵機和控制器用于飛行過程中為獲得最佳飛行效率而將翅膀軸向扭動。

撲翼結構采用的是兩段式的翅型,即拍打過程中帶有折疊過程。靠近仿生海鷗身體的一段翅膀稱為主翼,遠離身體的一段翅膀稱為副翼。鳥翼的結構十分精巧,想要完全真實的模仿對于現(xiàn)在的技術而言是十分困難的。所以主、副翼結構的設計主要需要滿足：1)翅膀的上下拍打運動；2)翅膀下行程時主翼和副翼向外舒展；3)翅膀上行程時主、副翼折疊。根據(jù)上述設計需求,提出了傳動效率高且結構簡單可靠的機構設計,機構簡圖如圖8所示。

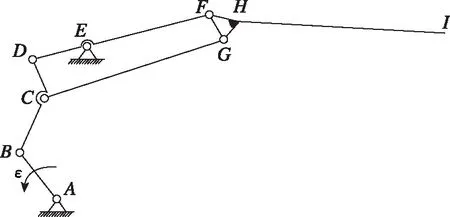
圖8 主翼和副翼機構簡圖Fig.8 Schematic diagram of main wing and aileron mechanisms

從圖8中可以看出,桿件AB是一個曲柄,與桿件BCD鉸接一起,帶動主翼桿件DF和CG,在桿件加入固定件E,使機構固定位置的同時達到上下?lián)鋭拥脑O計要求；連接件FHG加入一段連接主翼桿件DF和CG,另一端采用固定連接副翼桿件HI,連接件FHG的另一個設計作用使主翼在下行程中副翼桿件向外舒展,主翼在上行程中副翼相對向相反方向運動,達到相對主翼折疊的效果,這樣能最大效率地減小空氣阻力，實現(xiàn)功率的最大化；∠BCD的大小和CD的長度都經(jīng)過試驗確定，以確保其在運動時滿足下行程時主翼和副翼向外舒展、上行程時主翼和副翼折疊的設計要求。

1.2.3 傳動結構設計

因為要使兩端的翅膀完全對稱運動,所以傳動設計選擇了精準度較高、需要在頻繁且重復的工況下有較為優(yōu)異的穩(wěn)定性、運用較為廣泛的直齒輪傳動。在傳動裝置中還設計了二級減速裝置,使最終輸出裝置的轉速大幅減小。根據(jù)以上目標所得設計方案,如圖9所示。

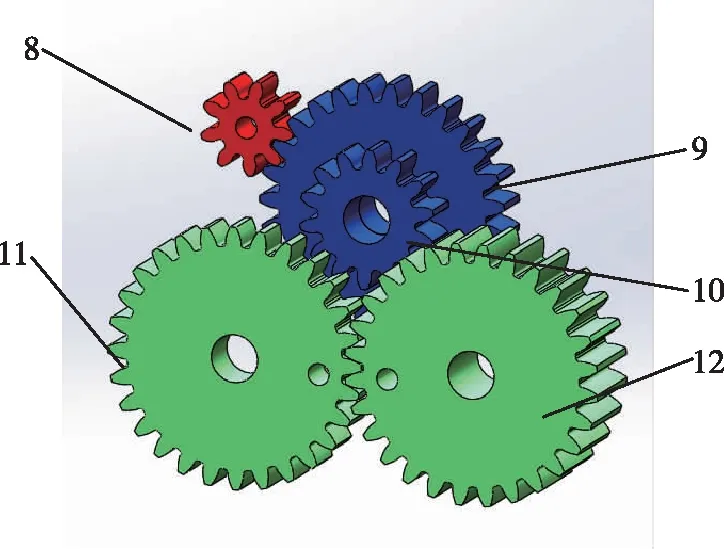
圖9 傳動齒輪設計Fig.9 Transmission gear design

傳動裝置中設計了二級減速裝置如圖9所示,其中所有齒輪的模數(shù)都為m=2,齒輪8為主動齒輪,齒數(shù)為9,通過與電機連接帶動整個齒輪副轉動。齒輪9(齒數(shù)為27)與主動齒輪8外嚙合,與齒輪10(齒數(shù)為14)同軸固定,目的是使齒輪9和齒輪10以同一角速度旋轉,同時小齒輪8為主動齒輪嚙合齒數(shù)較大的齒輪9可以達到減速增扭矩的效果。齒輪8、9、10組成了一個二級減速傳動齒輪副,達到降低轉速、增加扭矩的目的。齒輪11和齒輪12在其上打孔并在后期加裝在撲動機構上,目的是充當撲動主、副翼的兩個曲柄。齒輪11和齒輪12模數(shù)和齒數(shù)都相同,外嚙合達到兩側翅膀完全對稱運動的目的,齒輪12較厚,后部與齒輪10嚙合。整個齒輪副依據(jù)機械裝配的原理,通過機身的桿件和軸承與機身進行軸向和徑向的固定。

1.2.4 頭部和尾部結構設計

結合三點彎曲試驗的特點，采用對接的釬焊接頭形式，硬質(zhì)合金放在Cr12鋼上，中間為CuMnCo釬料，并用Mo絲控制釬縫的寬度。

通過對海鷗的仿生學和運動學研究了解其飛行特點,在海鷗轉向、起飛和降落的過程中,頭部和尾部都有參與運動,并且頭尾的作用在這些動作的過程中舉足輕重。以海鷗飛行過程中轉彎為例,首先海鷗會調(diào)整雙翼的撲動幅度和頻率,同時擺頭和甩尾控制身體平衡,這樣通過翅膀兩側不同的推力和升力差來達到轉向的目的。

由于頭部在飛行中只起到轉向的作用,所以在設計時只考慮流線型線條形狀,設計模型如圖10所示。有一定弧度的尾部可以在飛行時提供部分一定的升力和推力,所以為了彌補不能做到雙翼不同頻率撲動所帶來的部分飛行靈活性缺失,將尾部的形狀設計符合空氣動力學原理,如圖11所示。頭部和尾部中心位于同一根軸線上,通過中心桿件兩端與頭尾部的操縱圈的球鉸鏈鉸接,可以各個方向運動并靈活承受來自各翼面的壓力。

圖10 頭部機構設計Fig.10 Head mechanism design

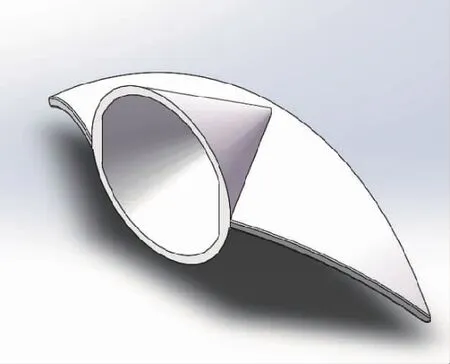
圖11 尾部機構設計Fig.11 Tail mechanism design

頭部和尾部分別通過兩根鋼絲與機身較靠后的兩個控制器相連,這個控制首尾部的控制器又稱為舵機,如圖12所示。舵機通過與控制器相連輸出扭力帶動操作桿,操縱桿連接鋼絲控制頭部和尾部,鋼絲一側張緊一側放松,連接鋼絲張緊的一側就會向內(nèi)回縮；兩側的鋼絲都放松時,該側零件就會相對身體向下；兩側鋼絲都張緊,該側零件就會相對身體向上。仿生學在觀察海鷗運動時發(fā)現(xiàn)，海鷗的頭部和尾部的朝向總是相反的,所以在設計時需用到兩個舵機,每一個舵機都有兩個控制桿,分別控制來自頭部和尾部的鋼絲的松緊,有效地保持整個身軀的平衡。

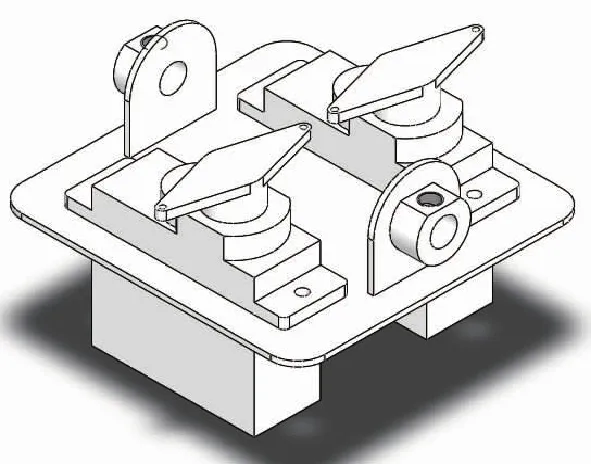
圖12 舵機機構設計Fig.12 Design of steering gear mechanism

2 運動學及仿真

2.1 運動學建模

撲翼機構采用雙曲柄雙搖桿機構,產(chǎn)生兩側為完全對稱的運動,故在運動學建模時,僅分析單側撲翼機構的撲動情況,之后可以由此結論推導出雙翼的運動規(guī)律。

根據(jù)設計的結構,用Visio軟件將撲動機構的右半部分的機構簡圖畫出,如圖13所示。對該結構進行運動學建模需要運用坐標法和矢量法,所以在這里將A點作為整個撲動結構笛卡爾坐標系中的原點,即坐標點A(0,0)。各桿件的長度以及固定點E點坐標皆為已知量。lAB=20,lBC=65,lCD=16.55,lDE=55,lDF=355,lCG=343.39,lGF=22,lFH=23.26,lGH=30.84,lHI=384,lBD=80.30,∠BCD=155°,∠FHI=154.54°,坐標點E(47.55, 95.57)。設定桿AB為主動旋轉部件,轉動角速度為ω(單位為rad/s),假設桿件AB與x軸正方向所成的角度為θ1,故由角位移方程可以易知θ1=ωt,所以點B的坐標是一個有關于時間的關系式,即B(lABcosωt,lABsinωt)。

連接BD、BE已在圖13上標出。在笛卡爾坐標系內(nèi),假設BE與x軸正方向之間的夾角為β,β∈(0,π),BD與x軸正方向的夾角為θ2,θ2∈(0,π),當0<θ2<π/2 時翅膀處于上行程,當π/2<θ2<π 時，翅膀處于下行程。因為點E也是一個關于坐標系固定的點,所以假設EF段與x軸正方向的夾角為θ3,θ3∈(0,π/2)。

圖13 右側撲翼機構簡圖Fig.13 Schematic of the flapping wing mechanism on the right

關于坐標點D(xD,yD),根據(jù)其位置的三角函數(shù)關系,可得

(1)

角度β、∠DBE、θ2和θ3都可由各桿件的位置和特征長度,經(jīng)過三角函數(shù)的變換所得

(2)

(3)

θ2=β+∠DBE

(4)

(5)

關于坐標點F(xF,yF),可通過位置關系得

(6)

坐標點C(xC,yC)是桿件BCD上的點,根據(jù)桿組關系式易知

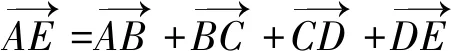
(7)

已知B、D點的坐標,將式(7)的矢量關系式分解成兩個相關的坐標關系式

(8)

式中，θ4是水平方向正方向與BD連線之間的夾角,θ5是Y軸正方向與桿件DC之間的較小的夾角。θ4和θ5之間存在的關系式如下

∠BCD=θ4+θ5

(9)

根據(jù)式(8)和式(9)可容易求出θ4和θ5關于時間t的關聯(lián)式,將關聯(lián)式帶入式(8)即可得到坐標點C的關聯(lián)式。

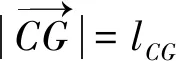
(10)

同理,可得F點坐標(xF,yF)

(11)

在得到坐標點F和坐標點G的關系式后,可以通過余弦定理可以計算出lFI的長度

(12)

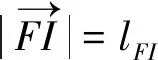
(13)

為了方便計算,將運動學建模所建立的所有公式導入MATLAB進行計算,最后通過式(13)推導出撲翼邊緣,即坐標點I關于角速度ω和時間t的坐標表達式,暫時取角速度ω=8rad/s,取坐標點I在運動一個周期內(nèi)每間隔0.01s時的坐標匯總,在Excel中導入并畫出各點連線出副翼尾部在一個周期內(nèi)的運動軌跡,所得的運動軌跡圖像如圖14所示。

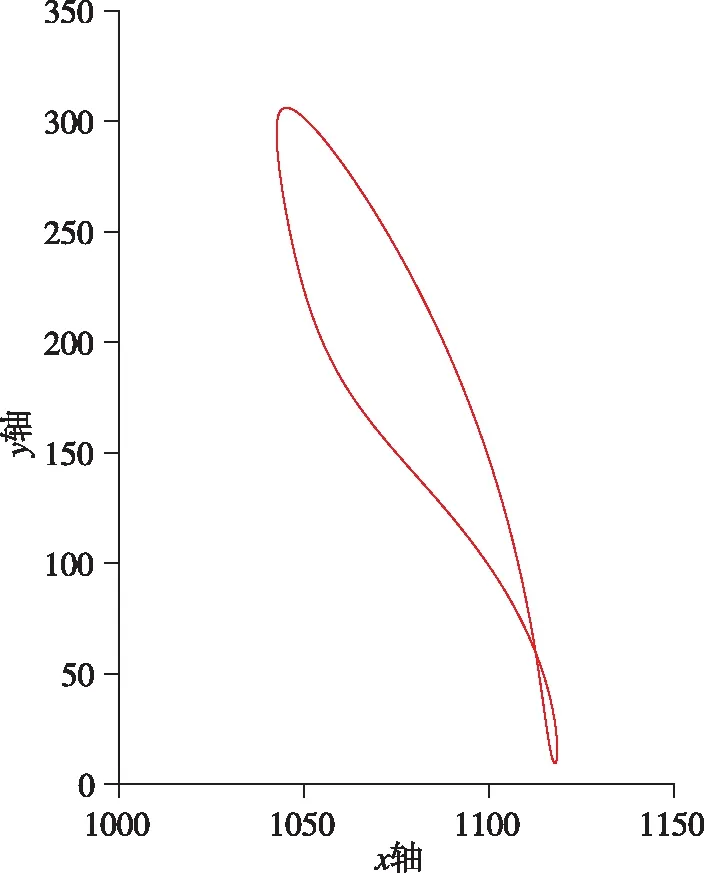
圖14 坐標點I運動軌跡Fig.14 Coordinate point I motion curve

2.2 模型仿真

在進行動力學電腦模型仿真之前,首先需要把在SolidWorks軟件內(nèi)建立的所有零件模型進行整合和裝配。裝配要求符合實際情況,并且需要設定固定數(shù)值的驅(qū)動力和運動限制,最后將模型的運動方式模擬出來,畫出翅膀模型的邊緣運動曲線,最后將曲線導出與理論分析結果進行對比。

撲翼飛行結構最主要的部分就是撲翼結構,為了避免其他零件對模擬產(chǎn)生的不可預計的影響以及減少計算量,將模型的其他零件進行壓縮,僅留下主要的撲動零件,如圖15所示。運用SolidWorks內(nèi)部運動學仿真插件Motion,對撲翼構件的運動方式做一個設定。在運動算例中首先插入一個旋轉馬達,根據(jù)上文提到海鷗在巡航飛行時的撲動頻率為5Hz左右,設置馬達為逆時針旋轉方向,等速300r/m旋轉,馬達帶動最小的主動輪旋轉,具體設置如圖16所示。接著對該運動算例進行分析,插入一個翅膀邊緣點,對該點進行路徑分析。

圖15 運動仿真簡化模型Fig.15 Simplified model of motion simulation

圖16 旋轉馬達設置Fig.16 Rotary motor settings

計算出的副翼末端的位移位置曲線為近似余弦曲線,如圖17所示。同時還計算出了該點的線性速度和線性加速度隨時間的變化,分別如圖18、圖19所示。

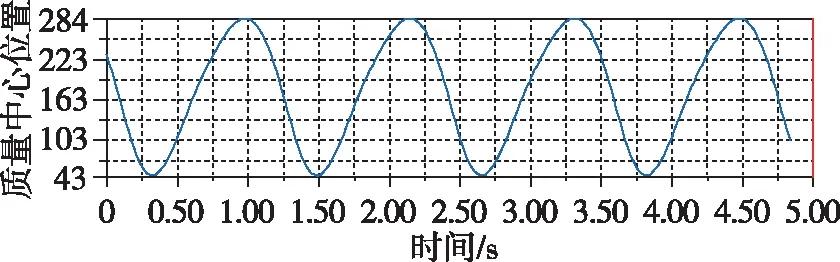
圖17 副翼位移曲線Fig.17 Aileron displacement curve

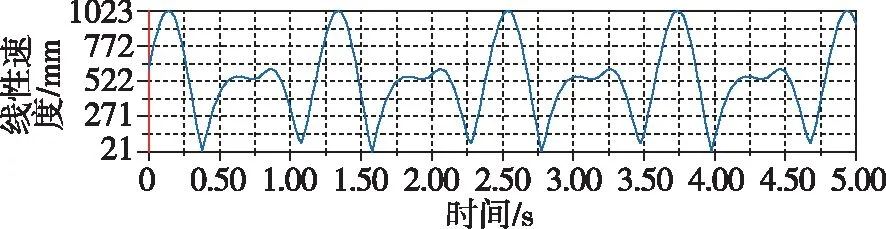
圖18 副翼線性速度曲線Fig.18 Aileron linear velocity curve

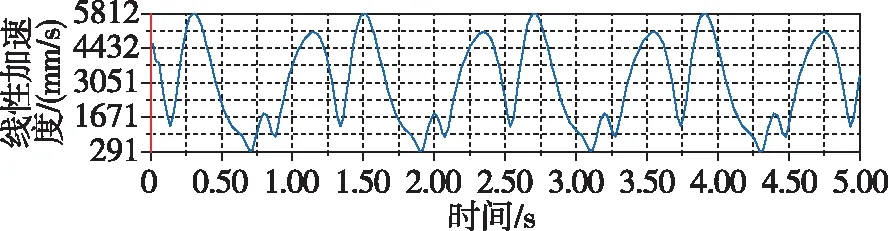
圖19 副翼加速度曲線Fig.19 Aileron acceleration curve

取副翼尾部最末端的點在運動時每間隔0.01s的坐標點,將所得的數(shù)據(jù)導入Excel并作圖,生成撲動路徑曲線,如圖20所示。

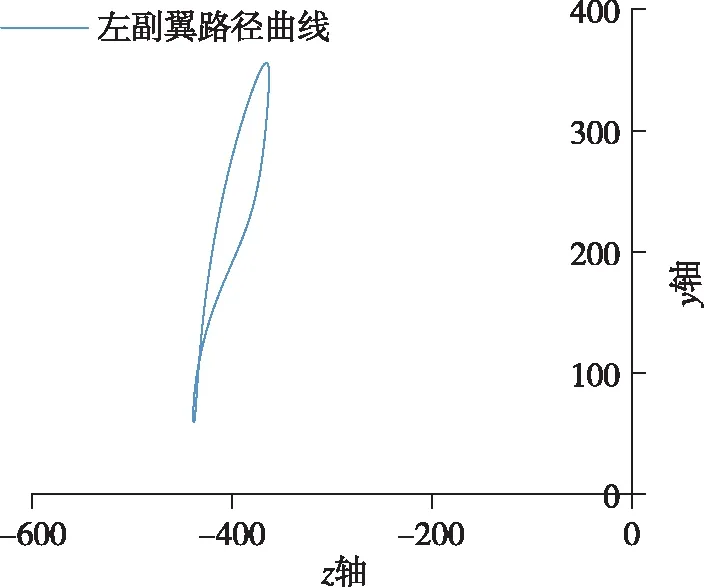
圖20 撲動路徑Fig.20 Flap path curve

本文同時也對主翼桿件的位置、線性速度以及線性加速度進行了分析,分析所得曲線如圖21～圖23所示。

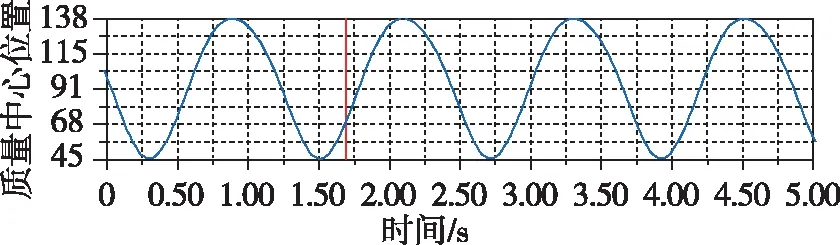
圖21 主翼位移曲線Fig.21 Main wing displacement curve

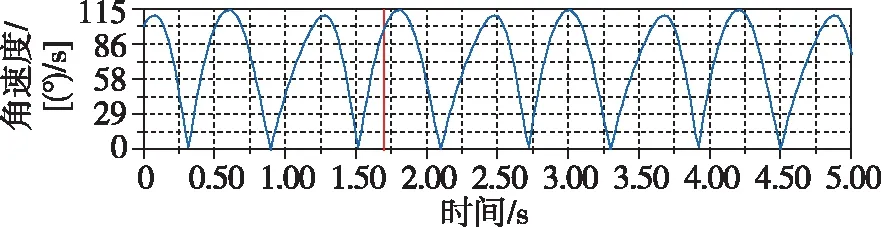
圖22 主翼線性速度曲線Fig.22 Linear velocity curve of main wing

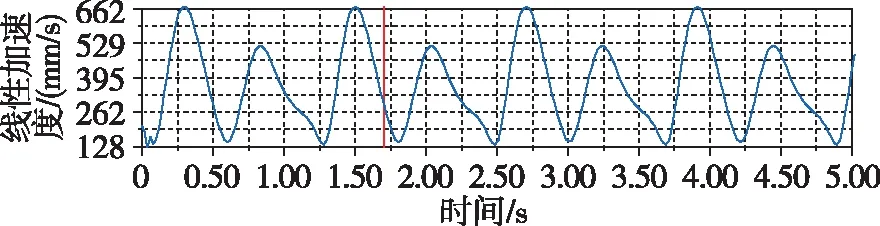
圖23 主翼線性加速度曲線Fig.23 Linear acceleration curve of main wing

通過對模型進行建模分析和研究,可以清晰看出所設計的結構運動性能完全符合海鷗的運動特征。副翼翅膀在下行程時,由于空氣阻力的作用,速度先快后慢,很好地將動能轉化為飛行時所需的升力。而在上行程時由于設計的曲柄具有急回特性以及撲翼的折疊運動,翅膀在行程內(nèi)雖然受到空氣阻力,但是由于機構特性受力面較小,所以加速度有明顯的上升。主翼翅膀的運動過程比副翼翅膀更為簡單,位移曲線更趨近于正弦曲線,速度也十分平穩(wěn),只在運動方向改變時有速度的突變,加速度方面也是在翅膀下行程時較大,能更好地、更高效地為飛行提供足夠的升力。從主翼和副翼的速度對比中可以看出，副翼最大速度約是主翼的10倍,設計效果優(yōu)良。從撲動路徑上可以看出，副翼在下行程時具有伸展動作,上下?lián)鋭拥那€接近“8”字型,成功模擬了海鷗翅膀的撲動路徑規(guī)律,在輔以軸向副翼后,扭轉時能很好地節(jié)省部分功率,十分符合理論計算的預期。

3 結論

本文對撲翼機器人結構進行了研究,通過對相關文獻和科研成果進行整理和分析,對多自由度撲翼飛行機器人結構進行設計和分析,從結構設計、運動學分析、建模和仿真模擬等角度開展研究并取得了一些成果。

從仿生學角度出發(fā),在分析了海鷗的飛行特征后,結合目前較為流行的撲翼結構設計,提出了一種具有折翼過程的撲動機構。在整體模型的基礎上完善了撲翼機構、傳動機構以及頭部和尾部的設計。將設計好的數(shù)學模型進行運動學的理論分析,證明了設計的機構具有急回特性,采用SolidWorks軟件將建立的所有模型結構根據(jù)實際要求進行裝配,實現(xiàn)了運動模擬。在軟件內(nèi)Motion的仿真結果與理論分析結果基本吻合,證明了設計結構的合理性和可行性。