某分布式驅動電動汽車復合制動策略設計＊

余卓平 史彪飛 熊璐 韓偉

（1.同濟大學，汽車學院，上海 201804；2.同濟大學，新能源汽車工程中心，智能汽車研究所，上海 201804）

主題詞：分布式驅動電動汽車 傳統制動系統 復合制動 電機發電效率

1 前言

能源危機和環境污染使得大力發展電能參與驅動的汽車成為時代的需求[1]，而分布式驅動電動汽車在動力性、經濟性和操縱穩定性方面都有集中式驅動系統無可比擬的優勢[2]。電動汽車可依靠復合制動系統進行制動能量回收，在電池技術不能取得突破性進展的情況下，能量回收是提高車輛續駛里程的重要途徑[3]。復合制動策略根據制動系統的不同分為并聯式和串聯式：并聯式指電機制動力直接按比例疊加到液壓制動力之上，適用于傳統制動系統，易于實現，成本低，但能量回收率較低；串聯式策略依靠制動踏板與制動液壓力解耦，可以優先使用電機力進行制動，能量回收率較高，但需要對制動系統進行重新設計，成本高[4]。

復合制動控制策略的研究中，制動力分配策略是其核心問題。謝布克大學的Nadeau J等人提出了一種理想的制動力矩分配方法，使電機最大限度地參與汽車制動，通過跟蹤理想制動力分配曲線提高制動效率，制動能量回收效果很可觀[5]。Poria Fajri博士等人提出了一種模擬電動汽車制動性能的新方法，并設計了既能滿足再生制動與液壓制動限制條件又能保持汽車制動穩定性的制動控制器[6]。清華大學呂辰提出了兼顧制動能量回收效率和制動踏板感覺的復合制動控制策略，解決了能量回收效率與制動踏板感覺之間的沖突問題[7]。

制動力分配策略研究主要集中于在一定制動需求下，如何分配前、后制動力以及如何進一步分配液壓制動力與電機制動力，而很少考慮在一定的電機制動力需求下，如何分配前、后電機制動力（對于分布式驅動車輛）。另一方面，制動過程中電機的發電效率與其當時的轉速和轉矩有關，因此，如何根據電機的工作狀態實時調整前、后電機制動力的分配以獲得最高的整體發電效率具有科研價值和實際意義。

本文以某分布式驅動電動汽車為研究對象，針對傳統制動系統，提出一套詳盡的復合制動策略設計方法，并在此基礎上提出考慮電機發電效率的經濟性優化策略，以提高續駛里程。

2 車輛改制前、后的制動特性分析

2.1 車輛改制情況

本文所研究的分布式驅動電動汽車原車為集中電機驅動的前驅車，改制后為前軸集中電機驅動，后軸輪轂電機驅動的分布式驅動汽車。改制過程中，為加裝后軸輪轂電機而減小了后軸制動器，導致后軸制動力大幅減小。根據改制前、后的制動器參數計算得到，改制前制動器制動力分配系數（前制動器制動力與汽車制動器總制動力之比）β1=0.678，改制后制動器制動力分配系數β2=0.901。

2.2 制動特性分析

原車總的制動特性及改制前、后踏板制動特性曲線如圖1所示。原車總制動特性包括液壓制動和0.1g的滑行再生制動，車輛改制過程中，前軸制動器參數不變，因此，改制后，在相同的制動踏板行程下，車輛制動減速度變為改制前的β1/β2=0.752倍。

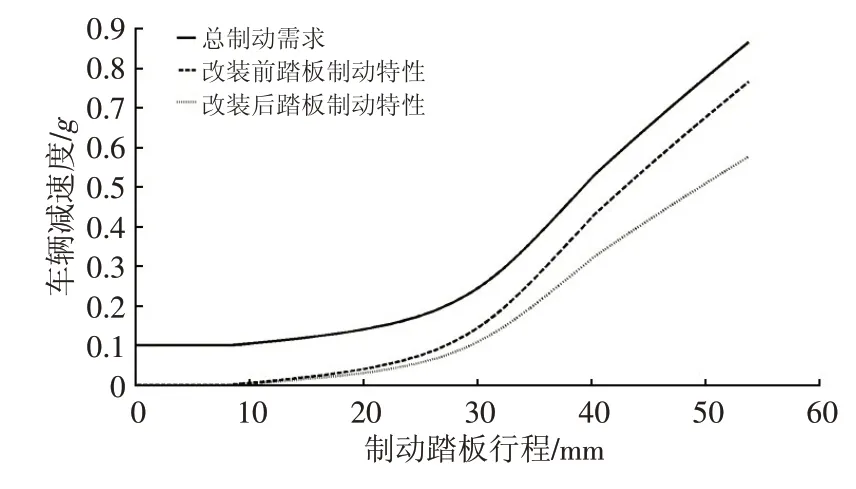
圖1 踏板制動特性

2.3 前、后制動力分配分析

為了保證制動時汽車的方向穩定性和足夠的制動效率，聯合國歐洲經濟委員會制定的ECE R13對雙軸汽車前、后輪制動器制動力提出了明確的要求。對于路面附著系數φ=0.2～0.8之間的各種車輛，要求制動強度z≥0.1+0.85(φ-0.2)，且車輛在各種裝載質量下，前軸利用附著系數曲線應在后軸利用附著系數曲線之上[8]。

根據整車參數繪制前、后制動力分配曲線如圖2所示。其中，Ⅰ曲線、橫軸與ECE法規線所包絡的區域即為ECE法規所要求的制動力分配范圍。由圖2可看出，改制前的β線滿足ECE法規且更貼近于Ⅰ曲線，制動效率較高，改制后的β線也滿足ECE法規，但其遠離Ⅰ曲線，制動效率低。

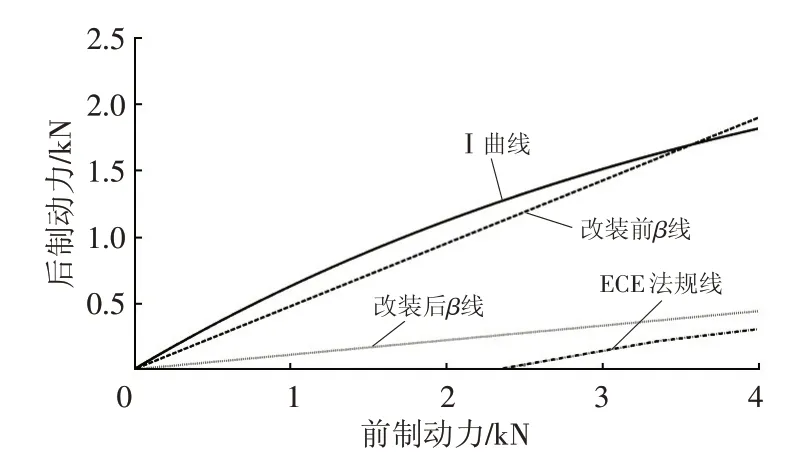
圖2 前、后制動力曲線

3 復合制動策略開發

為了保證車輛改制后的制動踏板感覺盡量與原車一致，應使踏板行程與車輛減速度的關系盡量與改制前的關系接近。針對改制后的車輛，復合制動策略中將滑行再生制動擬定為0.1g左右，再通過后軸電機主動制動，將制動踏板的制動特性解析成原車踏板的制動特性，即可滿足上述設計目標，總體思路如圖3所示。

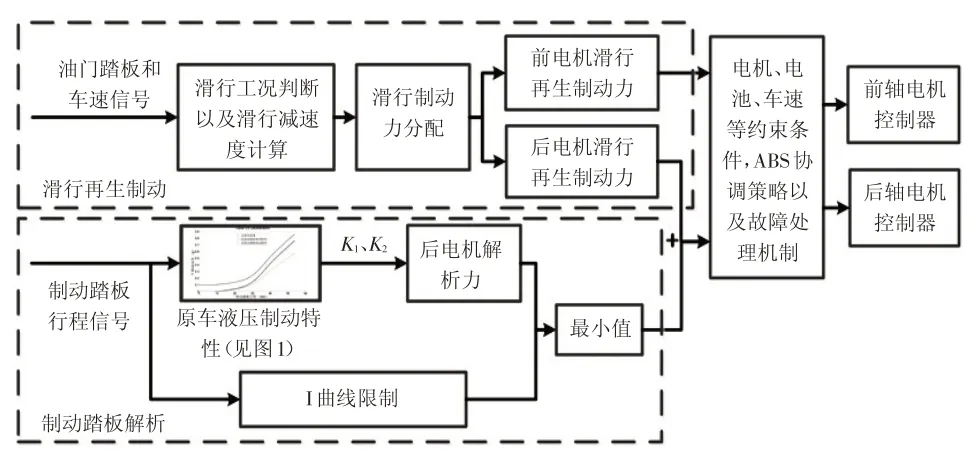
圖3 總體策略框圖

3.1 制動踏板解析

在駕駛員踩下制動踏板時，利用后軸電機的制動力主動補償后軸制動器改制后損失的液壓制動力，使最終的前、后制動力分配比等于β1。具體方法為：將原制動踏板特性中的制動減速度乘以(1-β1/β2)，即為在此踏板開度下，后軸電機應補償的當量制動減速度，再通過整車質量和車輪半徑等參數將其換算成電機力矩，如圖4所示。

每個后輪轂電機的解析力為：

式中，zj為解析出的制動強度；K1=1-β1/β2；K2=Gr/2；G為整車質量；r為車輪滾動半徑。

圖4 制動踏板解析

3.2 滑行再生制動

滑行再生制動即當駕駛員放松油門踏板后，利用電機回饋制動以模擬傳統內燃機汽車的發動機制動而進行能量回收[9]。

要實現0.1g的滑行制動減速度，只要滿足前、后軸總的電機制動力為0.1g即可，因此前、后電機力按照如圖5所示的z=0.1線分配即可（Ⅰ曲線下方）。z=0.1線的解析式為：

式中，F1、F2分別為前、后軸制動力。

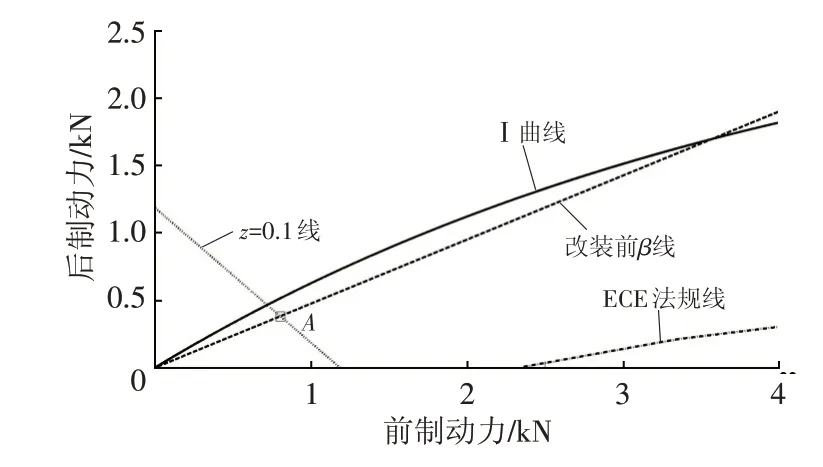
圖5 滑行再生制動力分配

理論上F1、F2有無數種分配方法，設z=0.1線與β線交于A點，考慮以下問題：分配點在A點之上時，若再疊加液壓制動力，即將β線上移，則在制動強度需求較大時，后軸制動力會超過Ⅰ曲線，有后軸先抱死的風險；分配點在A點之下時，若再疊加液壓制動力，即將β線下移，則雖能保證前輪先抱死，但制動效率降低。因此，將滑行制動時的前、后電機力分配點定為A點，此時前、后軸電機制動力分別為：

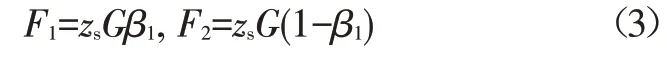
對應前、后電機的滑行再生制動轉矩分別為：

式中，zs為滑行制動強度；ig為減速器傳動比；η為減速器傳動效率。

文獻[10]、文獻[11]指出，一般取zs=0.05g～0.1g，且隨車速增大而增大。因此將滑行再生制動力定為隨車速線性變化的線性函數，車速為v1=10 km/h時對應的滑行制動強度為Z1=0.05，車速為v2=120 km/h時對應的滑行制動強度為Z2=0.1，即：

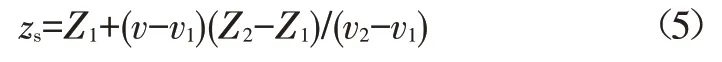
4 經濟性優化策略

4.1 策略介紹

考慮到總的制動需求以及改制后的液壓制動特性均已知，將其做差即可獲得總的電機制動力需求，則只需考慮如何分配前、后電機力。3.2節中的滑行制動力是基于原車β線進行分配的，簡單可靠，但并沒有充分考慮電機的工作效率，本文考慮電機發電效率進行經濟性優化。

集中電機和輪轂電機的效率曲線分別如圖6和圖7所示，二者效率的分布和數值并不完全相同。電機發電效率與其轉速和轉矩有關，二者又分別與車速和電機制動需求相關。因此，在變化的車速和變化的總電機制動需求下，逐次計算不同后軸電機力分配系數下的總電機效率，如圖8所示，尋找出在某一車速和總電機制動需求下，使所有電機效率之和最大的電機力分配系數，最優的后軸電機力矩分配系數Krear（取值范圍為0～1）如圖9所示。計算結果表明，在所有情況下，將電機制動力全部分配給后軸電機時總發電效率最高。

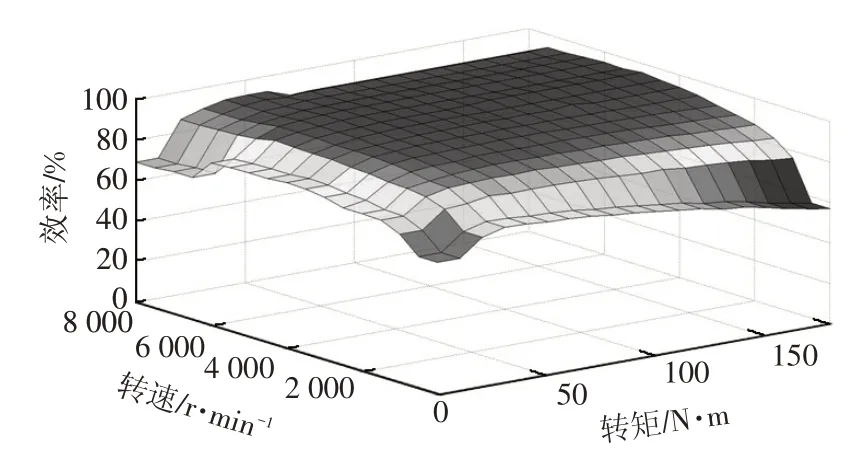
圖6 集中電機效率曲線

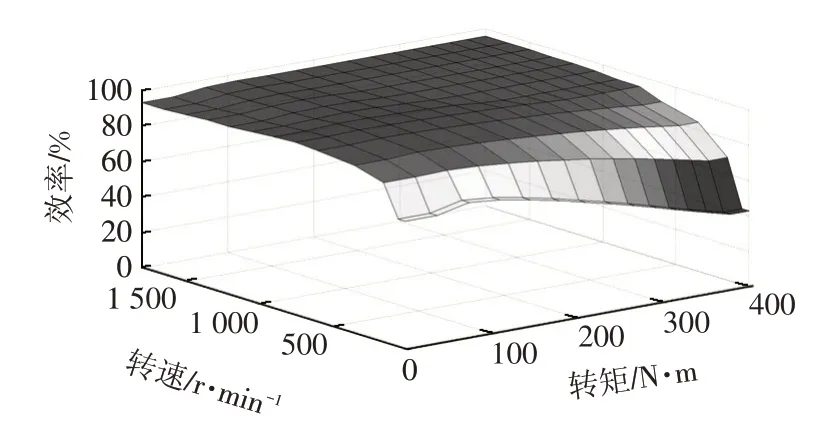
圖7 輪轂電機效率曲線

圖8 電機總效率計算

4.2 策略實施

在滑行制動時，將全部電機力分配給后軸電機，會使制動力分配越過Ⅰ曲線，不滿足ECE法規，因此，為了盡可能將制動力分給后軸，總的制動力應按照Ⅰ曲線進行分配。此時，前、后制動力分別為：

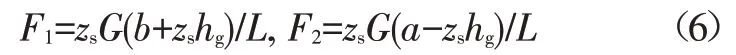
對應前、后電機的制動轉矩分別為：

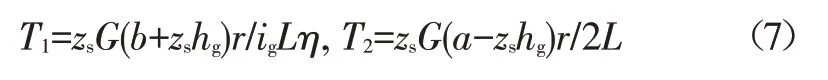
式中，a、b=L-a分別為前、后到質心的距離；hg為質心高度；L為軸距。

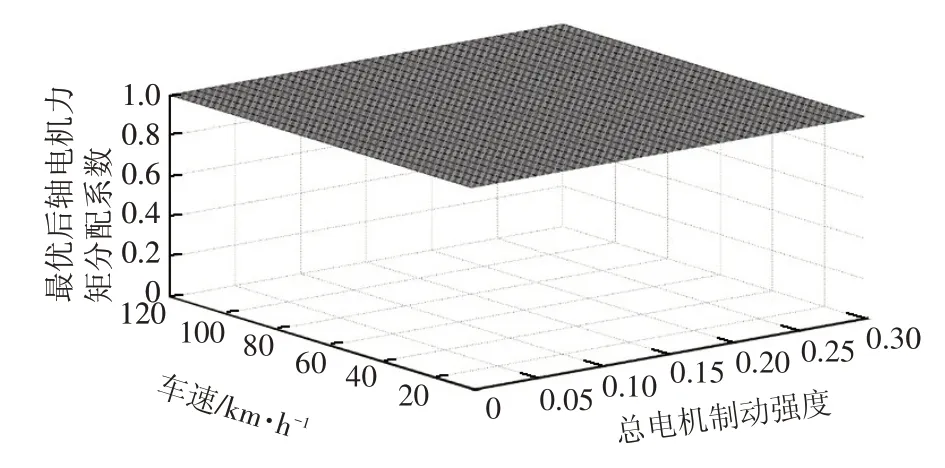
圖9 離線計算最優前、后制動力分配系數

分配點如圖10中B點所示。

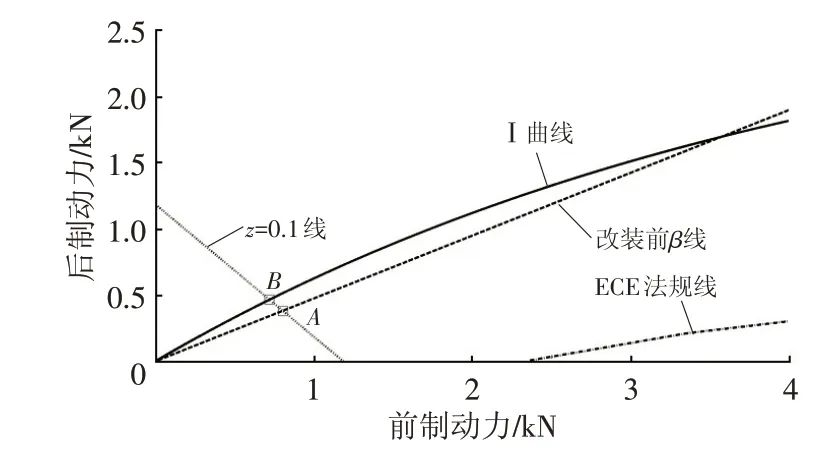
圖10 經濟性優化策略

行車制動時，由3.1節可知，駕駛員踩下制動踏板后，優先將踏板解析出的后電機制動力全額分配給后軸電機，隨著制動需求增加，總制動力分配將從B點出發并沿著平行于β1線的方向增長，此時，檢測總的制動力分配是否超越了Ⅰ曲線，一旦超過Ⅰ曲線，則約束后電機解析力，使總制動力沿著Ⅰ曲線分配，如圖11所示。

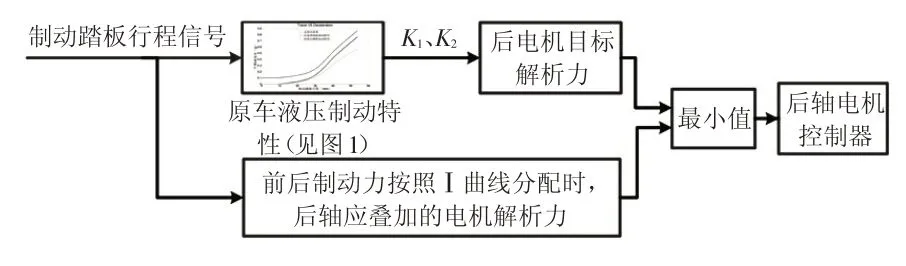
圖11 后軸電機踏板解析力矩

Ⅰ曲線約束計算方法為：

(zs+zj)為當前總制動強度，對應于Ⅰ曲線上的后制動力為：

考慮在當前滑行制動強度下，沿用改制后的制動踏板特性，則在當前踏板開度下，總的后制動力為：

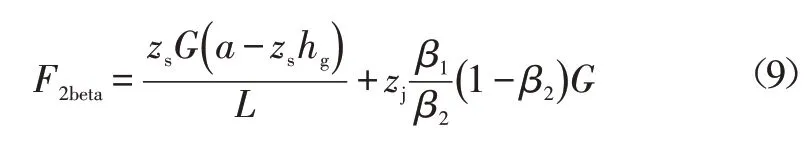
因此，若令后軸制動力按照Ⅰ曲線分配，則當前單個輪轂電機應疊加的電機力矩為：

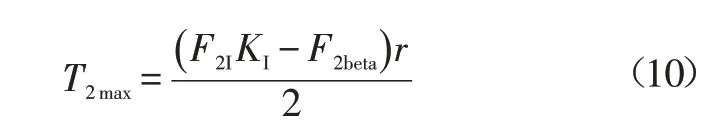
式中，KⅠ為Ⅰ曲線安全系數，為防止制動力分配越過Ⅰ曲線，取KⅠ=0.9。

取T2j與T2max的最小值作為最終的制動踏板解析力矩。

5 仿真分析

5.1 仿真模型的建立

在AVL Cruise軟件平臺上進行整車建模，如圖12所示。

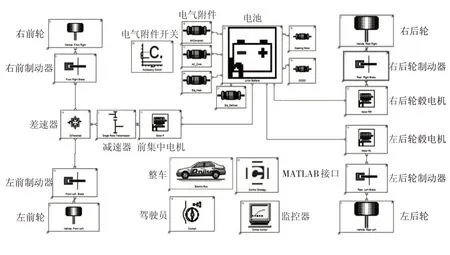
圖12 AVL Cruise整車模型

AVL Cruise車輛模型主要參數如表1所示。

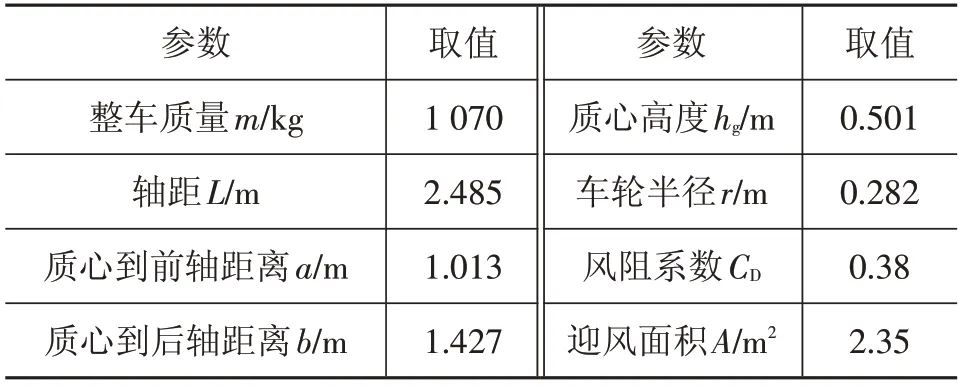
表1 整車模型主要參數

在MATLAB/Simulink軟件平臺上搭建復合制動控制策略，如圖13所示。

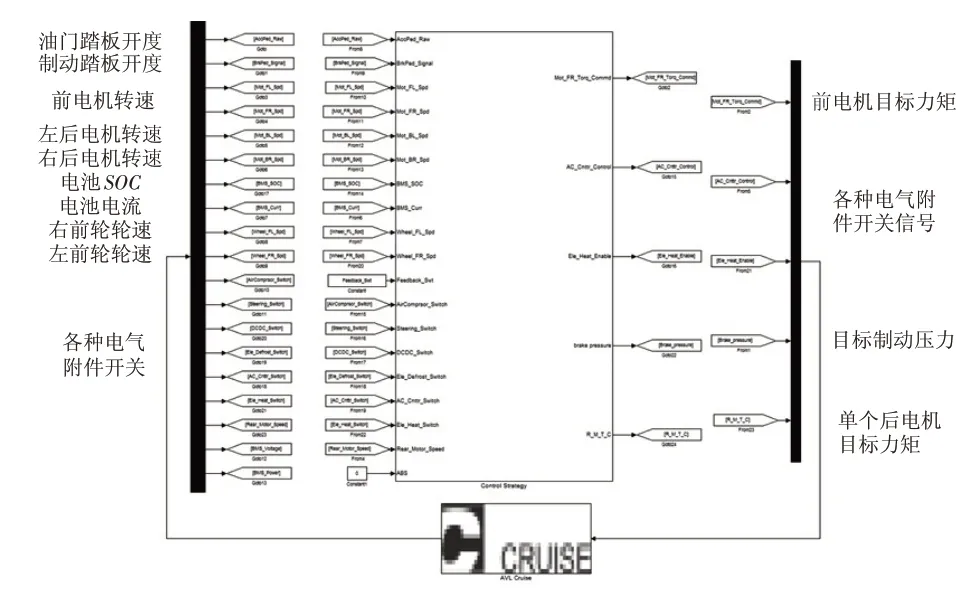
圖13 MATLAB控制策略模型

5.2 無經濟性優化的復合制動策略仿真

利用MATLAB和Cruise開展聯合仿真，仿真工況為NEDC循環。初始電池SOC為100%，仿真結束時電池SOC為10%，仿真結果如圖14所示。

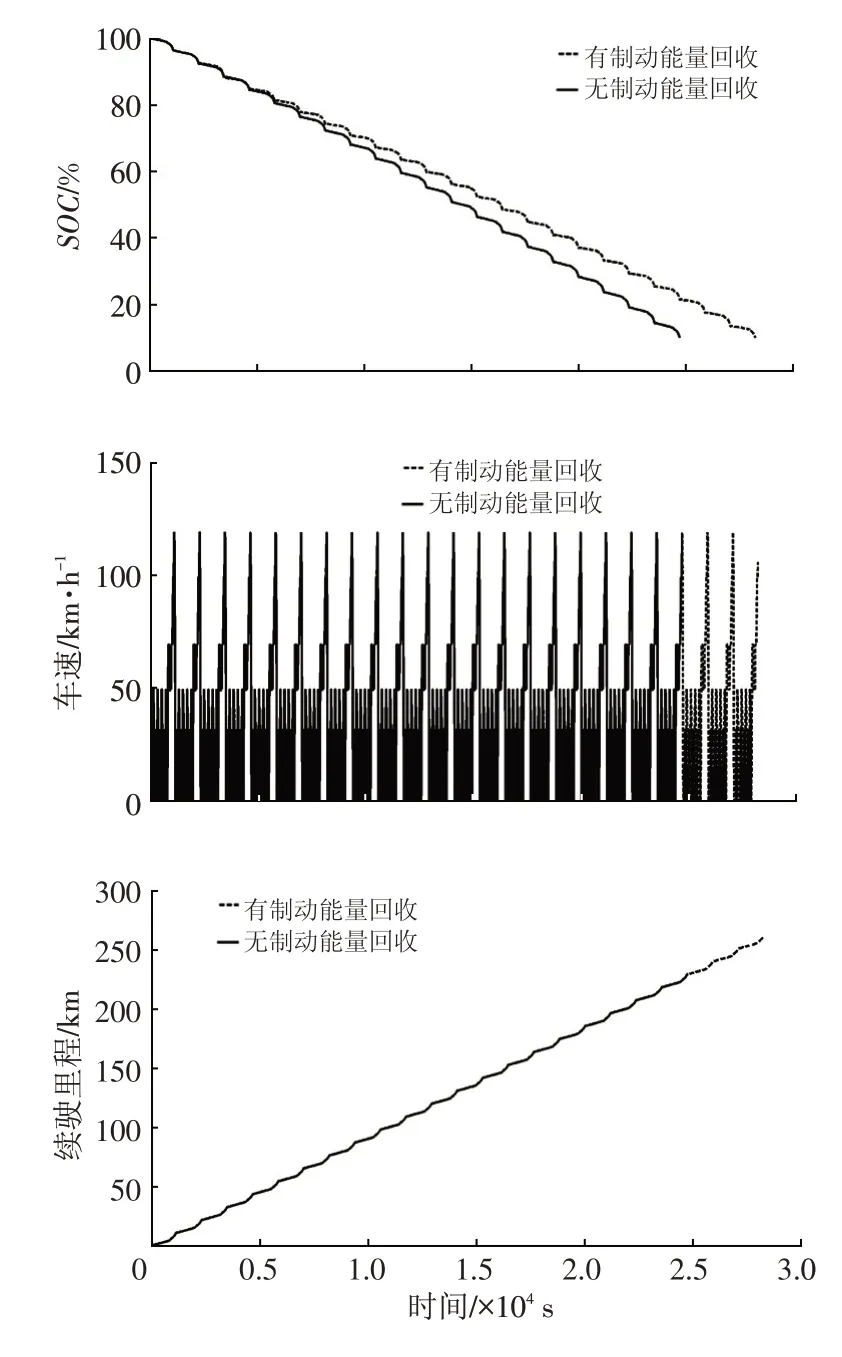
圖14 NEDC循環仿真

仿真結果顯示，有、無能量回收時續駛里程分別為260.9 km和228.5 km。因此，NEDC工況中無經濟性優化的復合制動策略續駛里程貢獻率為14.2%。有、無能量回收的SOC在90%～95%時開始出現差別，這是由于受到SOC限制，為避免電池過充電，在SOC低于90%～95%時才開始能量回收。SOC呈現波浪狀是由于電機發電功率與車速相關，每個波浪對應1個NEDC循環。

5.3 復合制動經濟性優化策略仿真

在同樣仿真工況下，采用經濟性優化策略，仿真結果如圖15所示。

仿真結果顯示，有能量回收時續駛里程為263.8 km，相比于無經濟性優化的復合制動策略提高了1.2百分點，這一方面是因為制動力分配點A點與B點相距較近，兩種策略的前、后電機力分配差別不大，另一方面，雖然從離線計算結果來看，把電機力盡量分配給后軸電機整體效率較高，但從電機效率曲線上看，后軸電機平均效率比前軸電機平均效率只高約3百分點，前、后電驅動系統的發電效率本身差別不大。

5.4 電機再生制動力對比

1個NEDC循環下有、無經濟性優化策略的電機制動力對比如圖16和圖17所示，其中電機力矩為正表示驅動，為負表示制動。

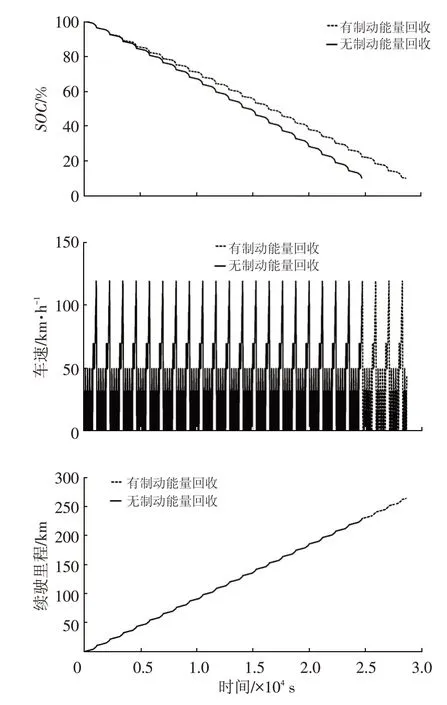
圖15 經濟性優化策略NEDC循環仿真

圖16 有、無經濟性優化的前軸電機力矩對比

圖17 有、無經濟性優化的后軸電機力矩對比

由圖16、圖17可以看出，復合制動策略對于驅動幾乎無影響，而對于制動，經濟性優化策略的前軸電機轉矩略小于無經濟性優化策略的前軸電機轉矩，相應地，后軸電機轉矩略大于無經濟性優化策略的后軸電機轉矩。仿真結果表明，經濟性優化策略的電機力更多地分給了發電效率較高的后軸電機，從而提高了總的能量回收率。

6 結束語

本文基于某款改制后的分布式驅動電動汽車，分析其改制前、后的制動特性，并提出了一套詳盡的復合制動策略設計方法。以原車的制動特性為目標，設計了考慮電機發電效率的復合制動經濟性優化策略。仿真分析結果顯示，不帶經濟性優化的復合制動策略續駛里程貢獻率為14.2%，考慮了電機發電效率的復合制動經濟性優化策略的續駛里程貢獻率為15.4%，所提出的復合制動經濟性優化策略對于前、后電機具有不同發電效率的分布式驅動電動汽車能產生更高的續駛里程貢獻率。