基于偏好誘導量詞的個性化推薦模型

郭凱紅 韓海龍

(遼寧大學信息學院 沈陽 110036)

隨著互聯網時代的到來，信息過載問題也變得越來越嚴峻，用戶很難在擁有眾多信息的產品中挑選出自己的最愛.個性化推薦系統為解決這一問題應運而生.目前，個性化推薦算法大致可分為5類：基于內容的推薦[1-3]、基于關聯規則的推薦[4]、基于知識的推薦[5]、協同過濾推薦[6]以及混合推薦[7].這其中，基于內容的推薦算法應用較為廣泛.傳統基于內容的推薦算法理論依據主要來源于信息檢索和信息過濾，該算法需要了解項目的屬性特征，通過分析用戶歷史行為記錄，構建用戶興趣偏好向量.該算法的優點是推薦的結果比較直觀，易于解釋，但是對于項目的特征選擇及復雜屬性處理效果略遜一籌，并且需要分析屬性間的依賴關系，還要面對新用戶的冷啟動等問題.針對以上不足，有學者從不同角度對這一算法給予改進和完善.李宇琦等人[1]提出一種基于網絡表示學習的個性化商品推薦算法，在各項評測指標上均有顯著提高.黃金超等人[2]則借助機器學習中分類算法的一些技巧，利用計算偏好分構造偏好度特征，提出一種基于偏好度特征的個性化推薦算法，具有一定的通用性，但仍存在矩陣稀疏、新用戶冷啟動等問題.

本文基于有序加權平均(ordered weighted aver-aging, OWA)及個性化建模思想，提出一種用戶偏好誘導的模糊量詞，并應用于個性化產品推薦.首先給定一組由多個備選方案構成的多屬性樣本數據，僅要求用戶根據自己的態度偏好或主觀評判，提供一個關于這組備選方案的優劣排序；根據這個排序序列，基于OWA思想并利用理想解法(technique for order preference by similarity to ideal solution, TOPSIS)方法，構造用戶期望值提取模型，以獲取特定偏好態度條件下用戶關于此樣本信息的期望值，再從中抽取偏好、態度等個性化信息，生成針對該用戶的個性化模糊量詞；最后利用該量詞對新產品屬性值進行OWA數據集成，從而實現個性化產品推薦.值得注意，在所提方法中，為獲取用戶期望值，僅要求用戶提供關于樣本方案的主觀排序(在個性化推薦應用中，樣本方案的主觀排序可從用戶的歷史瀏覽記錄中獲取)，對用戶的能力水平、專業知識、經歷經驗等差異性特質要求不高，目標模型構造精巧、實現簡單、可操作性強，相比文獻[8-10]的直接方法有極大優勢，由此確定的個性化量詞模型在實際應用中可面向不同層次、不同水平的用戶進行針對性的產品推薦，具有較強的實用性和靈活性.迄今，未見與本文用戶期望值提取模型相同或相似的研究文獻或報告.

1 相關工作

近年來，基于多屬性決策的個性化推薦逐漸成為研究的熱點.這類方法將決策思想及模型應用于個性化推薦中，得到一些較好的結果，比較典型的有混合多準則分析[11-15]、基于偏好的多屬性信息評價[16-19]等.基于模糊量詞的推薦模型并不多見，相關研究文獻極少.李微娜[3]從用戶偏好角度提出一種基于OWA算子的個性化推薦方法，利用Web用戶反饋的不完全偏好信息并結合用戶個性特征，實現待評價方案的OWA數據集成，進而計算出方案的優先順序，得出最終的推薦方案.該方法將決策分析中經典的OWA算子引入個性化推薦中，對本文工作確有一定的啟發作用.

事實上，Yager[20]提出OWA算子實現對數據排序位置加權，而非傳統算子對指標或數據本身加權，集成過程能夠靈活反映不同主體的偏好或態度，可直接應用于個性化推薦中.Yager[21]進一步強調OWA算子的集成效果依賴于OWA權重，并提出一種利用模糊語義量詞獲取OWA權重向量的有效方法.語義量詞的概念最早由Zadeh[22]提出，并利用模糊子集形式化定義語義量詞，將量詞分成兩大類：絕對量詞和相對量詞.絕對量詞，如不多于5個、至少20個等；相對量詞，如很少、大約一半、至多30%等.Yager[21]進一步將相對量詞細分為3種：正則遞增單調(regular increasing monotone, RIM)量詞、正則遞減單調(regular decreasing monotone, RDM)量詞以及正則單峰單調(regular unimodal monotone, RUM)量詞.注意到RDM量詞是RIM量詞的反義，而RUM量詞可以表示為RIM與RDM這2種量詞的交合，故應用中只考慮RIM量詞即可.模糊量詞在理論分析(計算機科學特別是人工智能)及實際應用中具有重要作用[20,23-31]，而針對量詞本身的研究文獻卻并不多見.Yager[23]介紹了一系列預定義的RIM量詞函數，研究了參數分配與偏好態度之間的關系.注意多樣的態度類型及特性并非通過簡單的預定義量詞及其參數分配就能夠合理反映出來.Ying[24]提出一種量詞的Sugeno積分語義，即量詞由一系列模糊測度表示且其命題真值由Sugeno積分求得.Liu[32-33]提出一種帶有生成函數的等差RIM量詞，研究了該量詞的數學性質及其潛在的應用.Guo[8]提出一種樣本信息期望值誘導的個性化RIM量詞，研究了其數學性質并應用于不確定性決策中.Guo[9]，Guo & Xu[10]進一步研究并完善了這類量詞的幾何光滑、保形插值、逼近速度等數值特征，由此提出這類量詞的多種函數表示形式.事實上，這類量詞具有較強的個體針對性，能夠很好地反映用戶的主觀偏好、決策態度等個性特征.注意到用于生成該類量詞的關鍵數據信息，即用戶期望值，是在設定的理想環境下采用一種比較直接的方法提取實現，在實際應用中可能會有一定的局限性.

2 理論基礎

2.1 OWA算子

Yager[20]于1988年提出OWA集成算子的概念，定義為

(1)

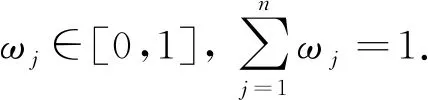
Yager[21]強調指出OWA集成效果依賴于伴隨向量Ω，并提出一種利用模糊量詞Q獲得OWA權重向量的有效方法，即

(2)

FQ(x1,x2,…,xn)=FΩ(x1,x2,…,xn)=

(3)

式(3)稱為模糊量詞誘導的OWA算子[21].

為考察OWA權重向量的分布所對應的態度值，Yager[20]引入態度特性(attitudinal character)的概念，定義為

(4)

易知，AC(Ω)∈[0,1].具體地，當Ω→(1,0,…,0)T，則AC(Ω)→1，表示用戶更偏好于數值較大的參數，這顯然是一種積極的態度；當Ω→(0,0,…,1)T，則AC(Ω)→0，表示用戶更偏好于數值較小的參數，這顯然是一種消極的態度；當Ω→(…,0,1,0,…)T或Ω→(1n,1n,…,1n)T時，AC(Ω)≈0.5，表示用戶既不偏好于較大的參數值也不偏好于較小的參數值，這是一種中庸態度.結合式(2)(4)，可建立態度特性與模糊量詞之間的關系，即:

(5)

進一步可得[23]:

(6)

Yager[21]進一步將量詞誘導的OWA算子推廣到更一般的環境，即參數值帶有權重信息的情況.設A為m個備選方案集合，即A={a1,a2,…,am};c為具有不同權重信息的n個指標集合，即c={c1,c2,…,cn}.對于?a∈A，ci(a)表示方案a關于指標ci的值，yj(a)為ci(a)(i=1,2,…,n)中第j個最大值，uj(a)是與yj(a)相對應的指標權重信息.此時，OWA權重可通過以下方式獲得:

(7)

FQ(c1(a),c2(a),…,cn(a))=

FΩ(c1(a),c2(a),…,cn(a))=

(8)

注意對于每個方案a，ci(a)(i=1,2,…,n)的排序都有可能不同，這將導致uj(a)(j=1,2,…,n)順序的不同，進而有Sj(a)的不同，最終使得每個方案所對應的OWA權重也不同.這實際上體現了OWA數據集成的特點，即將主觀偏好與客觀數據有機結合，使得兩者相輔相成、相得益彰.

2.2 TOPSIS方法

TOPSIS法又稱為理想解法[34]，是一種有效的多指標決策方法.在使用前，應先將指標值做標準化處理.設決策矩陣X=(xij)m×n，指標權重向量W=(w1,w2,…,wn)T，X的標準化矩陣Y=(yij)m×n，而

(9)

其中，i=1,2,…,m,j=1,2,…,n;J+代表效益型指標集，J-代表成本型指標集.經過式(9)標準化后，矩陣Y中所有成本型指標值均轉換成效益型值.

根據標準化矩陣Y，定義正、負理想解V+及V-分別為

(10)

(11)

定義方案ai到正、負理想解的距離分別為

(12)

(13)

則方案ai的相對貼進度可定義為

(14)

顯然，當ai=V+，Ci=1；當ai=V-，Ci=0.Ci值越大，對應的方案越優良.

3 用戶偏好誘導的模糊量詞

3.1 樣本數據的指標權重

顯然，di越小方案越優.為了確定指標權重wj，構造最優化模型

求解此模型，作拉格朗日函數:

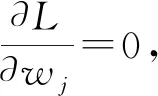
解得

j=1,2,…,n.

(15)

3.2 基于偏好的用戶期望值

對于3.1節給定的多屬性樣本數據，可利用TOPSIS方法中相對貼進度的定義，得到一組客觀的方案排序序列.不失一般性，設樣本各方案所對應的相對貼進度滿足關系C1>C2>…>Cm，其中Ci是方案ai的相對貼進度，i=1,2,…,m，則樣本方案ai的客觀優劣排序為a1?a2?…?am.顯然，這是典型的傳統排序方法所得到的結果.

下面考慮基于用戶偏好的排序問題.假定用戶根據自己的主觀偏好或者決策態度，對該樣本數據中方案的主觀排序為b1?b2?…?bm，其中bk表示樣本方案ai(i=1,2,…,m)中用戶第k個最滿意方案，k=1,2,…,m，即對于該用戶而言，b1即是最滿意的方案，b2次之，bm是最不滿意的方案.顯然，這里考慮的主觀排序序列依賴于用戶的主觀偏好決策態度，與樣本方案的客觀優劣性無直接關系.

顯而易見，不同排序序列中的方案表現出不同的重要性.為了表達并區分這種重要性，需要分配各方案相應的重要性權值.一方面，對于由傳統TOPSIS方法得到的客觀排序序列a1?a2?…?am，可以使用相對貼進度表示這種重要性.在這種意義下，相對貼進度大者對應的方案具有較高重要性，相對貼進度小者對應的方案具有較低重要性.具體地，對于客觀排序序列a1?a2?…?am，a1所對應的貼進度值C1最大，客觀上具有最高重要性，應該分配最大的權值，a2次之，am則最不重要，對應的權值應該最小.鑒于方案的客觀重要性與其相對貼近度的一致性，可令weight(ai)=Ci，i=1,2,…,m.

另一方面，對于用戶給出的主觀偏好排序b1?b2?…?bm，b1是該用戶最滿意的方案，主觀上具有最高重要性，故應分配最大的權值，b2次之，bm對于該用戶來說則最不重要，應該分配最小的權值.類似于上述客觀排序序列中方案權值的分配策略，這里仍考慮使用相對貼進度實現主觀偏好排序中各個方案的重要性權值的分配.此時的分配策略是，用戶越滿意的方案，賦予的相對貼進度值就越大，即令weight(bk)=Ck，其中bk是所有ai(i=1,2,…,m)中用戶第k個最滿意方案，Ck是ak(k=1,2,…,m)的相對貼進度，滿足關系C1>C2>…>Cm.

綜上顯見，在同一個排序序列中，不同的方案具有不同的重要性，而對于同一個方案，在排序序列中所處位置不同，其重要性也不同.為進一步厘清備選方案的排序序列及其重要性權值分配策略之間的關系，需考察方案的不同排序序列中固有保持不變的因素.注意到上述2種主、客觀方案排序序列中，已分配的方案的重要性權值均滿足關系C1>C2>…>Cm，而C1,C2,…,Cm本質上可視為客觀排序序列a1?a2?…?am關于排序位置的重要性權值，即排序位置越靠前，該位置的重要性權值就越高.這意味著方案的重要性權值的分配與其所在排序序列中的具體位置緊密相關，更進一步，在用戶的主觀偏好排序意義下，方案重要性的分配并不依賴于方案本身，而依賴于它所在排序序列中的具體位置，位置越靠前，該位置上的方案就越重要，分配的重要性權值就越高，而對于某個排序序列的同一位置，不同的方案在該位置處應具有相同的重要性，應分配相同的重要性權值.

由此，可得出重要結論：用戶的主觀排序序列中各方案的重要性權值應與其所在位置的權值C1,C2,…,Cm相一致，即可令weight(bk)=weight(ak)=Ck，其中bk是所有ai(i=1,2,…,m)中用戶第k個最滿意方案，Ck是ak的相對貼進度，k=1,2,…,m，C1>C2>…>Cm.這一結論本質上與OWA權重向量的基本思想相一致.

為進一步闡明上述結論，方便后續的形式化操作，給出“備選方案-決策矩陣-重要性權值”的偏好有序結構為

(16)

其中，左側方案列中，bk為所有ai(i=1,2,…,m)中用戶第k個最滿意方案，中間決策矩陣中，pkj是bk關于指標cj的標準化指標值，右側權值列中，Ck(k=1,2,…,m)表示排序序列中第k個位置的權值，符號“↓”表示方案由優至劣，或權值由高到低.注意此時居中的決策矩陣P=(pkj)m×n已根據方案的主觀偏好排序b1?b2?…?bm對原標準化矩陣Y=(yij)m×n中的行向量重新做了相應的調整.

在這種偏好結構下，可計算用戶關于各個指標cj的期望值，即:

(17)

用戶期望值是構建個性化量詞的重要數據信息，對個性化量詞的性能起到決定性作用.文獻[8-10]采用一種相對直接的方法獲取用戶期望值，即降序重排樣本數據中各指標屬性值后，要求用戶根據自己的主觀偏好直接選取一組關于各指標的期望值.為此，用戶需要具有較豐富的領域知識和經歷經驗.相比之下，本文給出的模型只需用戶參考樣本數據，根據自己的偏好或態度提供一組關于樣本方案的主觀排序序列，由此提取用戶的期望值，對用戶的專業知識、能力水平、經歷經驗等差異性特質要求不高，具有更大的實用性和可操作性.

3.3 個性化模糊量詞建立

(18)

利用上述結果S，進一步建立由用戶偏好誘導的個性化量詞[8]:

(19)

其中,si由式(18)確定.由式(6)可得量詞Q?的態度特性[8]:

(20)

其中si由式(18)確定.注意當S→(1,0,0,…,0)T時，有λQ?→1-1(2m)，若m→∞，則λQ?=1，這顯然是積極的態度.當S→(0,0,…,0,1)T時，有λQ?=1(2m)，若m→∞，則λQ?=0，這顯然是消極的態度.當或S→(1m,1m,…,1m)T時，有λQ?≈0.5，這是一種近似的中性態度，特別地，當S=(1m,1m,…,1m)T或時，有λQ?=0.5，這顯然是完全的中性態度.

由此，本文提出一種較為新穎的模型用以提取用戶關于樣本信息的期望值，并據此建立針對此用戶的個性化量詞，稱之為用戶偏好誘導的模糊量詞，簡稱偏好誘導量詞.所提方法中用戶期望值提取模型構造新穎精巧，實現簡單方便，相比文獻[8-10]中的直接方法有極大的優勢.由此得到的量詞模型，具有較強的個體針對性，能夠很好地反映用戶的偏好、態度等個性特征，為其追求主觀偏好下的“最滿意方案”而非一般意義下的“最優方案”提供一種切實可行的判決標準和分析工具，在需要特殊考慮主體偏好、態度等個性特征的復雜環境中，如不確定性決策、個性化產品推薦等應用中，具有較高的實用性、靈活性和可操作性.

關于模糊量詞更多的函數表示、數學性質、一致性定理等內容，請參閱文獻[8-10,20-21,23].

3.4 偏好誘導量詞建模方法

綜上，給出偏好誘導量詞的建模方法為：

步驟0. 獲取樣本數據及用戶偏好排序序列(個性化推薦應用中用戶針對樣本方案的主觀排序可從其歷史瀏覽記錄中獲取).

步驟1. 由式(15)獲取樣本信息指標權重向量.

步驟2. 由式(12) ～ (14)計算樣本方案的相對貼近度，確定樣本方案的客觀排序序列.

步驟3. 根據用戶偏好排序序列重排樣本決策矩陣，由式(17)計算用戶期望值.

步驟4. 降序重排決策矩陣中各列屬性值，再由式(18)計算用戶關于樣本信息的態度向量.

步驟5. 利用所得態度向量，由式(19)建立個性化量詞.

步驟6. 利用所得量詞實現個性化推薦.

4 在個性化推薦中的應用

4.1 實例研究

本節應用3.3節所得的用戶偏好誘導的模糊量詞解決個性化產品推薦問題.算例中部分基礎數據改編自李微娜[3].

假定某購物網站銷售多個品牌筆記本電腦，顯示其屬性為價格c1、CPU速度c2、硬盤容量c3等3種，顯然c1為成本型指標，c2和c3為效益型指標.

首先從用戶網頁歷史瀏覽記錄中獲取用戶偏好信息.用戶通常通過點擊進入筆記本電腦的產品信息頁面，瀏覽一段時間后，可能會將感興趣的產品放入購物車中.根據歷史瀏覽記錄，發現用戶共瀏覽了5臺筆記本電腦，其屬性值標準化后如表1所示，其中，成本型指標c1的屬性值利用式(9)已轉換為效益型值.

Table 1 Specifications of Recently Visited Items表1 已瀏覽商品明細

利用Shahabi等人[35]提出的客戶追蹤機制原理獲取用戶瀏覽該網站的起始時間、對商品的點擊順序和次數以及瀏覽該網站的結束時間等信息，得到用戶關于以上產品的網頁使用行為如表2所示:

Table 2 Usage Behaviors on Web Pages表2 用戶頁面使用行為

由表2易知，用戶共點擊了6次有關筆記本電腦的信息頁面：首先點擊a1，用時7 s并將其放入購物車中，說明用戶對a1非常感興趣；然后點擊a5，用時9 s但并沒有放入購物車，說明對于a1和a5，用戶對a1更感興趣；接下來用戶點擊a2，用時10 s，可知此時對a5和a2，用戶對a2更感興趣；隨后用戶又再次點擊a5，用時2 s，此時用戶瀏覽a5共計11 s，因此相對于a2，a5是更理想的產品；同理可得用戶對a4的態度較a3更感興趣.

綜上分析，可依據是否將商品放入購物車、累積瀏覽某一特定商品的時長等網頁使用行為數據考察用戶對商品的偏好程度，從而得到該用戶對上述產品的主觀偏好排序，即:

ζ:a1?a5?a2?a4?a3.

至此，可根據該主觀偏好排序ζ，應用本文所提模型及方法建立針對該用戶的個性化量詞，其中，多屬性樣本信息已由表1給出.

步驟0. 已獲取樣本數據，即表1，以及用戶偏好排序序列，即ζ.

步驟1. 根據表1，得到產品的標準化決策矩陣:

利用式(10)(11)，定義正、負理想解分別為

再由式(15)得到指標權重向量:

W=(0.370,0.555,0.075)T.

步驟2. 利用式(12)(13)，計算各產品到正、負理想解的距離，再利用式(14)計算各產品的相對貼進度為

C1=0.930,C2=0.444,C3=0.523,C4=0.193,C5=0.628,

據此得到產品的客觀排序序列為

ο:a1?a5?a3?a2?a4.

相比較用戶的主觀偏好排序ζ:a1?a5?a2?a4?a3，兩者有一定的差異.

步驟3. 根據用戶的主觀偏好排序ζ重排決策矩陣Y，定義“備選方案-決策矩陣-重要性權值”的偏好有序結構為

再利用式(17)計算用戶的期望值，得到:

步驟4. 降序重排矩陣Y中各列屬性值，得到新矩陣記為

S=(0.042,0.277,0.610,0.056,0.015)T.

可以看出，有影響的權重分量集中分布在S的中間位置偏上，說明用戶稍微偏好數值較大的參數，對應于中性偏積極的態度.

步驟5. 利用獲得的向量S及式(19)，建立針對該用戶的個性化量詞，即:

進一步，利用式(20)得到對應的態度特征值:

λQ?=0.555.

顯然這是中性偏積極的態度.

步驟6. 下面使用所得量詞Q?通過OWA數據集成實現個性化產品推薦.假定該購物網站尚有未瀏覽待推薦的同類筆記本電腦5臺，標準化后的各屬性值如表3所示.類似地，成本型指標c1的屬性值利用式(9)已轉換為效益型值.

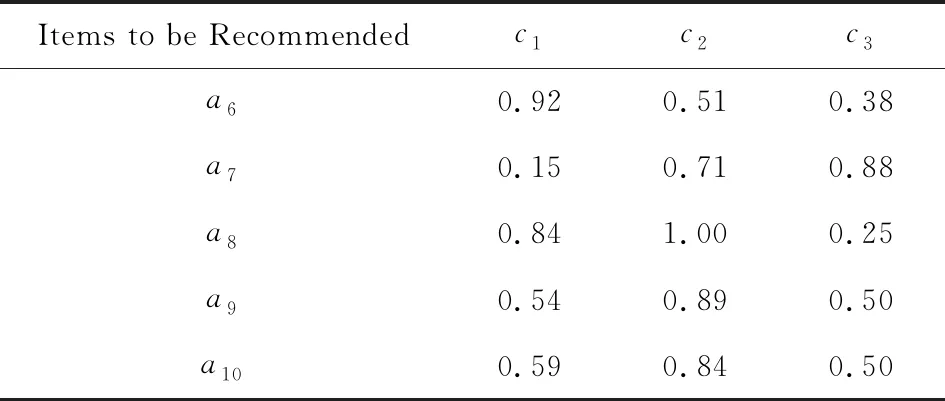
Table 3 Specifications of Items to be Recommended表3 待推薦商品屬性明細

據此得到待推薦產品的標準化決策矩陣:

令:

Ua6=(0.92,0.51,0.38)T,Ua7=(0.15,0.71,0.88)T,Ua8=(0.84,1.00,0.25)T,Ua9=(0.54,0.89,0.50)T,Ua10=(0.59,0.84,0.50)T.

為實現每個待推薦產品的OWA數據集成，首先利用已得到的指標權重向量W=(0.370,0.555,0.075)T，由式(7)計算每個待推薦產品的OWA權重向量，即:

Ω(Ua6)=(0.278,0.716,0.006)T,Ω(Ua7)=(0.016,0.921,0.063)T,Ω(Ua8)=(0.791,0.203,0.006)T,Ω(Ua9)=(0.791,0.203,0.006)T,Ω(Ua10)=(0.791,0.203,0.006)T,

注意到每個待推薦產品的屬性值的降序排列不同，導致其所對應的指標權重的順序也不同，最終使得每個待推薦產品所對應的OWA權重也不同.最后利用所得量詞Q?及式(8)實現每個待推薦產品的OWA數據集成，即:

FQ?(Ua6)=0.623,FQ?(Ua7)=0.677,FQ?(Ua8)=0.963,FQ?(Ua9)=0.817,FQ?(Ua10)=0.787,

顯然，推薦的順序為

a8?a9?a10?a7?a6.

即待推薦產品a6～a10中，a8為該用戶偏好下的最滿意產品，應優先推薦給該用戶，而a6為最不滿意產品，應最遲推薦給該用戶.在李微娜[3]的結果中，推薦次序為a8?a10?a9?a7?a6，與本文結果基本一致，只是a9與a10互換了位置.事實上，李微娜[3]在計算的最后階段，未考慮之前已獲得的指標權重，直接使用式(2)獲取OWA權重向量實現數據集成，而本文則自始至終充分考慮樣本數據的指標權重，在最后階段使用式(7)獲取OWA權重向量，實現數據的加權集成，所得的推薦順序更具可信性.

為進一步驗證所提模型的有效性，以下將針對相同的樣本數據(即表1)，采用其他3種不同方法，分別考查其推薦結果并與本文模型所得結果作比較，具體如表4所示.表4中，文獻[17,36-37]均假定用戶具有理性中性態度(與本算例中態度特征值λQ?=0.555相當)，分別使用OWA算子、S-HARA效用函數、C-GOWA算子等模型及方法實現新產品序列的計算.顯而易見，文獻[36-37]中的2種方法所得結果和本文一致，而文獻[17]方法所得結果和本文基本一致，只是a6和a7互換了位置.由此說明本文所提模型的有效性.

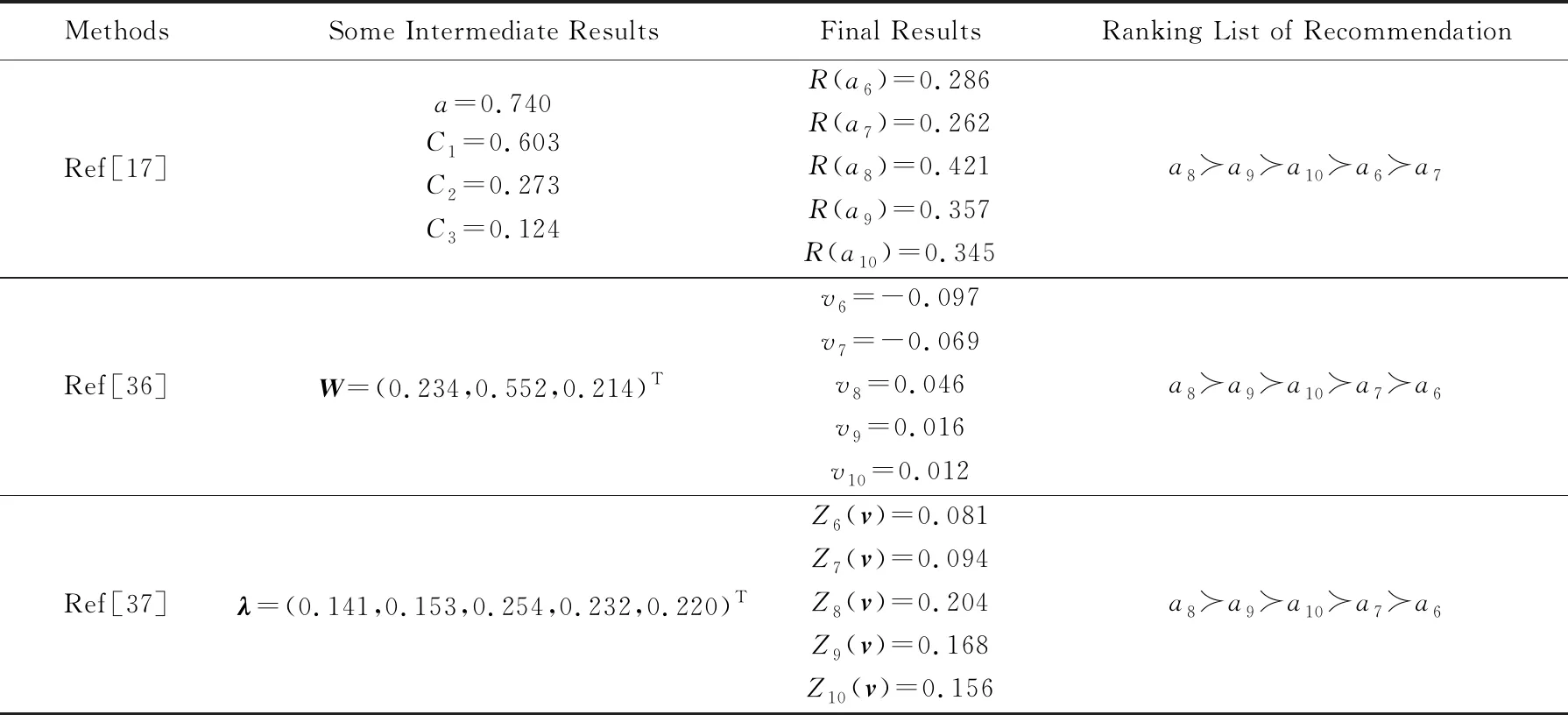
Table 4 Results from Different Methods表4 不同方法得到的結果

4.2 進一步討論

下面進一步討論樣本方案的不同主觀偏好排序對模糊量詞及新產品推薦的作用.首先考察不同主觀偏好排序對模糊量詞的作用.

1) 假定之前用戶針對產品a1～a5的主觀偏好排序為ζⅠ:a1?a5?a3?a2?a4.顯然這與4.1節所得的客觀排序序列ο完全一致.此時，根據ζⅠ重新調整決策矩陣Y，定義“備選方案-決策矩陣-重要性權值”的偏好有序結構為

在此偏好結構下，可得用戶期望值為

相比較4.1節所得的用戶期望值：

SⅠ=(0.053,0.430,0.457,0.046,0.014)T,

注意到有影響的權重分量集中分布在SⅠ的偏上位置，說明該用戶偏好數值較大的參數對應于積極的態度，所對應的量詞函數為

2) 假定用戶針對a1～a5的主觀偏好排序為ζⅡ:a4?a2?a3?a5?a1.顯然這與4.1節客觀排序序列ο完全相反.此時，根據ζⅡ重新調整決策矩陣Y，定義“備選方案-決策矩陣-重要性權值”的偏好有序結構為

在此偏好結構下，可得用戶期望值為

相比較4.1節所得的用戶期望值：

SⅡ=(0.034,0.090,0.150,0.664,0.062)T,

注意到有影響的權重分量集中分布在SⅡ的偏下位置，說明該用戶偏好數值較小的參數，對應于消極的態度，所對應的量詞函數為

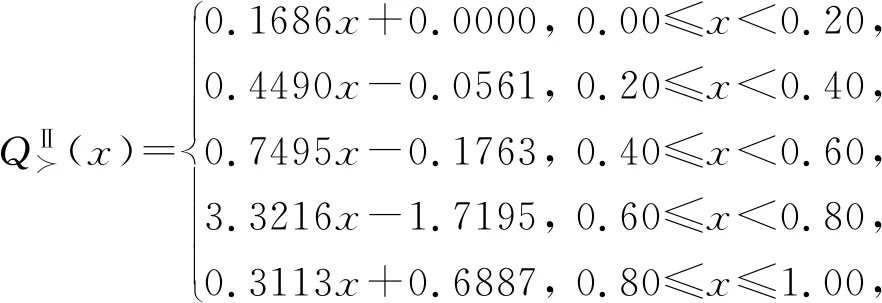
綜上易知，針對樣本方案的不同主觀排序能夠反映用戶不同的偏好及態度，進而對應于不同的用戶期望值及量詞函數，由此得到的個性化推薦序列也應該不同.為進一步表明上述觀點，表5給出以上所得不同量詞所對應的一些關鍵結果及其對新產品a6～a10的個性化推薦序列.同時，針對同一樣本數據的不同偏好排序，亦給出使用李微娜[3]方法所得到的推薦序列.

Table 5 Some Key Results from Different Preference Rankings for Sample Alternatives表5 不同偏好排序所對應的關鍵結果

相比之下，本文模型及方法設計新穎精巧，可操作性強，可面向不同層次水平、不同知識結構的用戶，利用他們的偏好信息反映其主觀個性特性，同時與客觀數據相結合，理性快捷地向其推薦相應態度偏好下的“最滿意方案”而非一般意義下的“最優方案”，具有更大的實用性和靈活性.

5 結 論

本文研究了多屬性樣本方案的重要性與其主觀偏好排序位置之間的關系，經形式化建模與分析后認為，用戶的主觀排序序列中各方案的重要性不依賴于方案本身的客觀屬性，而依賴于他們所在的主觀排序位置，排序位置越靠前，對應方案越重要.基于這種理解，提出一種新穎的用戶期望值提取模型，該模型構造精巧，實現簡單，對用戶的能力水平、專業知識、經歷經驗等差異性特質無特殊要求，具有較強的可操作性和靈活性.據此進一步建立由用戶偏好信息誘導的模糊量詞，該量詞具有較強的個體針對性，能夠很好地捕獲并反映用戶的偏好、態度等個性特征，為用戶追求主觀偏好下的“最滿意方案”而非一般意義下的“最優方案”提供知識支持.最后將所得模型及方法應用于個性化推薦中，以解決典型的產品推薦問題.更一般地，在需要特殊考慮主體偏好、態度等個性特征的復雜環境中，如不確定性決策、情境感知計算、個性化商品定制等，本文模型及方法仍具有實際應用價值.下一步工作將深入分析多屬性樣本數據的分布特征與樣本方案的主觀偏好排序之間的關系及其對期望值的影響及作用機理，同時針對所得量詞的幾何特征做進一步研究，以期得到同時具有充分光滑、保形插值、快速收斂等優良性質的至善的個性化模糊量詞.