基于最小二乘法的改進卡爾曼濾波算法

符 強， 陳孝倩， 孫希延， 任風華， 嚴素清

(1.桂林電子科技大學 廣西精密導航技術與應用重點實驗室,廣西 桂林 541004；2.桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004)

在室內、密集街區、山地、森林等微弱衛星導航信號環境中，由于遮擋和反射，衛星信號功率衰減并伴有多徑干擾和噪聲干擾，從而降低了碼環的跟蹤性能[1-2]。針對這些問題，現有的解決方案主要有3類：1)信號接收天線的空域處理方法，如扼流圈天線可以削弱來自地面和低仰角的多徑信號[3-4]；2)對跟蹤環路的相關器和碼鑒相器進行改進，如窄相關[5]和Strobe鑒相器[6-7]，這類方法雖然可提高抑制多徑干擾的性能，但也減弱了環路的跟蹤性能和噪聲抑制性能；3)基于估計原理的多徑估計方法，如Townsend等[8]采用多相關器結構得到多組相關值，通過迭代計算，得到估計的直達信號相關參數，以達到抑制多徑的目的。通過借鑒多徑估計延遲鎖定環路(MEDLL)中信號估計的方法，崔艷等[9]提出最大似然估計算法，利用最大似然估計原理在相關前估計出直達信號和多徑信號的各項參數，雖能很好地抑制了多徑，但也降低了噪聲抑制性能，且有計算量過大的問題。基于卡爾曼濾波的方法很多，其主要有2種實現結構：1)在碼環鑒別器和環路濾波器之間加入卡爾曼濾波器；2)用卡爾曼濾波器代替原有的鑒別器。卡爾曼濾波主要有線性卡爾曼濾波[10](Kalman filter，簡稱KF)、擴展卡爾曼濾波[11-12](extended Kalman filter，簡稱EKF)和平淡卡爾曼濾波[13](unscented Kalman filter，簡稱UKF)3種，其中EKF和UKF都是非線性的。采用非線性卡爾曼濾波雖然效果相對較好，但計算量很大；而采用線性卡爾曼濾波，計算量小，但存在濾波器發散的問題。

雖然研究者提出了很多基于卡爾曼濾波的碼跟蹤方法，但不管采用線性卡爾曼濾波還是非線性卡爾曼濾波，在這種濾波估計中，觀測值是唯一的信息源，但信息源中的噪聲誤差、系統誤差、觀測誤差、設備誤差等會降低濾波器的估計性能，使得采用現有卡爾曼濾波技術的碼跟蹤環的性能較差。為此，提出一種最小二乘算法與卡爾曼濾波相結合的改進算法。

1 衛星導航信號模型與構造

衛星導航接收機中，載波跟蹤環和碼跟蹤環共同組成接收機的跟蹤環路。載波跟蹤環對載波頻率和載波相位進行跟蹤。碼環對碼相位進行精確的估計和跟蹤，這是實現偽距測量和定位的基礎[14]。在存在多徑效應的弱信號環境中，全球定位系統(global position system，簡稱GPS)衛星信號可表示為

(1)

其中：i為各路信號分量；ai為信號幅度；ω為載波頻率；θi為第i路信號的載波初相位；c(t)為偽碼；τi為第i路信號與本地偽碼的碼相位差；D(t)為導航電文；n(t)為高斯白噪聲。這里τ0為直達信號與本地偽碼的碼相位差，是估計的目標參數。

設I路本地載波為sin(ω0t+θ0)，不考慮導航電文，則I路解擴后的相干積分值為

(2)

其中：

(3)

φi=(ω-ω0)Tcoh+(θi-θ0)；

(4)

(5)

其中：p(t)為服從N(0，σ2)的高斯白噪聲；Tcoh為相干積分時長；fe為載波頻率差；φi為載波相位差；Rc(·)為偽碼自相關函數。實際接收機中，由于載波跟蹤環對載波頻率差fe和載波相位差φi的精確跟蹤，將fe、φi看作已知的常數參數。

采用卡爾曼濾波器代替傳統碼環鑒別器處理多徑問題，通常建立狀態方程和觀測方程，對直達信號和多徑信號的碼相位等目標參數進行估計，抑制多徑效應。在這種方法中，由各相關支路解擴后的相干積分值組成的觀測值是卡爾曼濾波的唯一信息源。從式(2)可知，偽碼自相關函數是相干積分值的一個因子，這個因子包含噪聲誤差、系統誤差、觀測誤差、設備誤差等各種誤差，這些誤差會被帶入卡爾曼濾波對目標參數的估計中。如何尋求一種方法抑制或消除這些誤差，對自相關函數因子進行修正，使得觀測值更接近真實值，從而對直達信號和多徑信號的碼相位、幅度等目標參數進行更精確的跟蹤。

2 對相關函數因子的修正

為了便于推導，以接收到的衛星信號只包含一路直達信號和一路多徑信號的情形為例，推導的結果很容易推廣到更多路徑的情況。設某一I路相關支路的相關器與本地即時碼相關器的碼相位間距為δ，由式(2)可知，該支路的相干積分值為

R(t)=a0sinc(feTcoh)cos(φ0)Rc(τ0-δ)+

a1sinc(feTcoh)cos(φ1)Rc(τ1-δ)+p(t)，

(6)

每次相干積分值作為一個觀測值緩存于緩存模塊中，每M次相干積分進行一次環路更新。式(6)可寫成矢量形式

R=G·B+P。

(7)

其中：P為噪聲矢量；R為該相關支路的M次相干積分值組成的觀測矢量；G為量測矩陣；B為待估計的狀態矩陣。

R=[R1,R2,…,RM]Τ，

(8)

(9)

(10)

由最小二乘估計原理[15]可知，B的最小二乘估計為

(11)

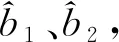
(12)

得到一個修正后的相干積分。對每條相關支路的相干積分中的自相關函數因子都用最小二乘算法進行修正，并得到修正后的相干積分，則可得一組無偏、均方誤差和最小的新的觀測值，組成觀測矢量zk，用于后續的濾波估計。

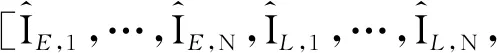
(13)

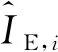
3 改進后的卡爾曼濾波在碼跟蹤中的應用

3.1 基于改進卡爾曼濾波的信號跟蹤模型

利用最小二乘算法修正相關函數因子的思想，構造一組無偏、均方誤差和最小的修正觀測值。改進卡爾曼濾波算法的碼跟蹤環實現結構如圖1所示。與傳統卡爾曼濾波算法不同，改進卡爾曼濾波算法在卡爾曼濾波器前加入最小二乘模塊，并在最小二乘模塊與積分累加器之間加入緩存模塊，用于緩存各支路解擴后的相干積分。為解決卡爾曼濾波器的發散問題，改進卡爾曼濾波算法加入了發散判斷控制模塊。

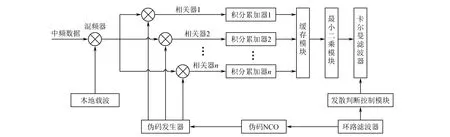
圖1 改進卡爾曼濾波算法的碼跟蹤環實現結構

設各相關支路的相關器相對即時碼相關器的碼相位間距為±δj，為了能夠估計多徑信號，并對直達信號進行精確碼跟蹤，選擇濾波器狀態量為

x=[a0a1τ0τ1]Τ。

(14)

其中：a0為直達信號的幅度；a1為多徑信號的幅度；τ0、τ1分別為直達信號和多徑信號相對本地偽碼的碼相位差。卡爾曼濾波器的狀態方程為

(15)

其中：wk為過程噪聲向量，其為零均值白高斯噪聲。設Qk是wk的協方差矩陣，Qk一般取對角矩陣，建立修正觀測矢量與狀態量之間的線性方程為

zk=Hk·xk+vk。

(16)

其中：Hk為測量矩陣,Hk的維數為4N×4；vk為測量噪聲向量。Hk的第i列(i=1,2,3,4)可由下述公式求得，

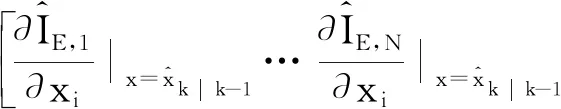
(17)

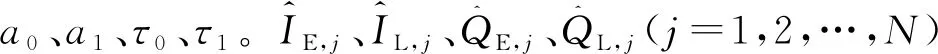
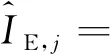
a1sinc(feTcoh)cos(φ1)Rc(τ1+δj)。

(18)

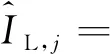
a1sinc(feTcoh)cos(φ1)Rc(τ1-δj)。

(19)

a1sinc(feTcoh)sin(φ1)Rc(τ1+δj)。

(20)

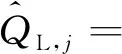
a1sinc(feTcoh)sin(φ1)Rc(τ1-δj)。

(21)

3.2 卡爾曼濾波器模塊

設I和Q支路分別采用了N組超前-滯后相關器，考慮下線性系統：

xk=F·xk-1+wk；

(22)

zk=Hk·xk+vk。

(23)

根據系統模型構建卡爾曼濾波基本方程：

(24)

Pk|k-1=FPk-1FΤ+Qk-1，

(25)

Kk=Pk|k-1HkΤ(HkPk|k-1HkΤ+Rk)-1，

(26)

(27)

Pk=(I-KkHk)Pk|k-1。

(28)

在卡爾曼濾波的實現過程中，測量噪聲的預測是非常關鍵的一步，很大程度上決定了卡爾曼濾波器的性能。此外，如何進行發散的判斷和修正也是至關重要的步驟。只有這樣，所設計的卡爾曼濾波器才能帶來預想的效果。

1)噪聲的理論分析。接收機中噪聲是白高斯噪聲，白高斯噪聲通過積分累加器的過程可近似為通過低通濾波器的過程，故接收機噪聲方差σ2=N0Bn/2，其中N0為雙邊帶頻譜功率密度，Bn=1/Tcoh為積分累加器的帶寬。測量噪聲協方差陣Rk由各測量之間的協方差組成。設n1、n2為I路上2條相關支路的信號，n3、n4為Q路上2條相關支路的信號，vn1、vn2、vn3、vn4為4條支路的噪聲，|ni-nj|為2個信號所在支路相關器之間的碼相位間距，

E[vn12]=E[vn22]=E[vn32]=E[vn42]=σ2。

(29)

由于I支路與Q支路的不相關性，有

E[vn1,vn3]=E[vn1,vn4]=E[vn2,vn3]=

E[vn2,vn4]=0。

(30)

設偽碼碼元長為Tchip，不同信號間的協方差為：

(31)

(32)

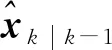
4 仿真結果與分析

采用GPS的1號衛星的偽碼，中頻為4.092 MHz，采樣頻率為16.368 MHz，相干積分時間為5 ms，每10次相干積分組成最小二乘模塊的觀測量。仿真有兩路信號，一路直達，一路多徑，多徑信號相對直達信號的碼相位時延為0.3碼片，幅度相對比例為0.5。

圖2為信噪比RSN=-25 dB時傳統卡爾曼濾波算法[10]和改進卡爾曼濾波算法的碼相位跟蹤誤差。從圖2可看出，當RSN=-25 dB時，傳統卡爾曼濾波的碼相位跟蹤誤差為-0.028～0.031碼片，改進卡爾曼濾波算法的碼相位跟蹤誤差為-0.022～0.018碼片，改進卡爾曼濾波算法的碼相位跟蹤精度稍高于傳統卡爾曼濾波算法。

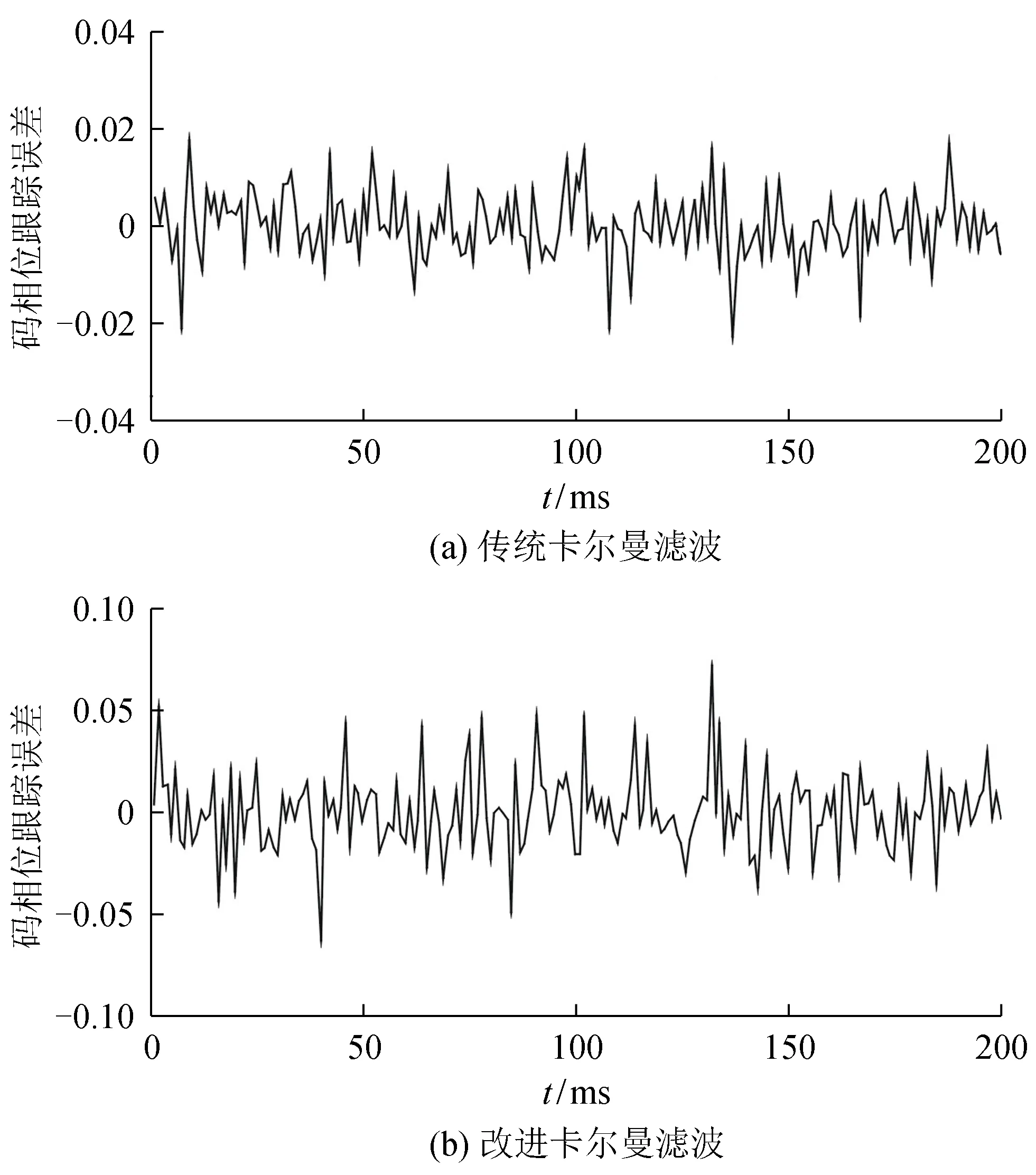
圖2 2種算法在信噪比為-25 dB時碼相位誤差對比

圖3為典型低信噪比RSN=-45 dB時2種算法的碼相位跟蹤誤差。從圖3可看出，隨著信噪比降至-45 dB，傳統卡爾曼濾波算法[10]的碼相位跟蹤誤差為-0.14～0.17碼片，而改進卡爾曼濾波算法的碼相位誤差為-0.06～0.08碼片，改進卡爾曼濾波算法的碼跟蹤精度明顯高于傳統卡爾曼濾波算法。

圖4為2種算法不同信噪比的碼相位均方根誤差(root mean square error，簡稱RMSE)。從圖4可看出，在信噪比為-45 dB時，改進卡爾曼濾波算法和傳統卡爾曼濾波算法[10]的碼相位RMSE分別為0.002 7碼片和0.043碼片，前者比后者要小很多。隨著信噪比的增加，2種算法的碼相位RMSE都有減小的趨勢。當信噪比增加到-24 dB時，改進卡爾曼濾波和傳統卡爾曼濾波的碼相位RMSE分別為0.001和0.004，相比于信噪比-45 dB的情形，2種算法的碼相位RMSE的差值減小，但前者仍然小于后者。其結果充分表明了改進卡爾曼濾波算法較傳統卡爾曼濾波算法的碼跟蹤性能更穩定。

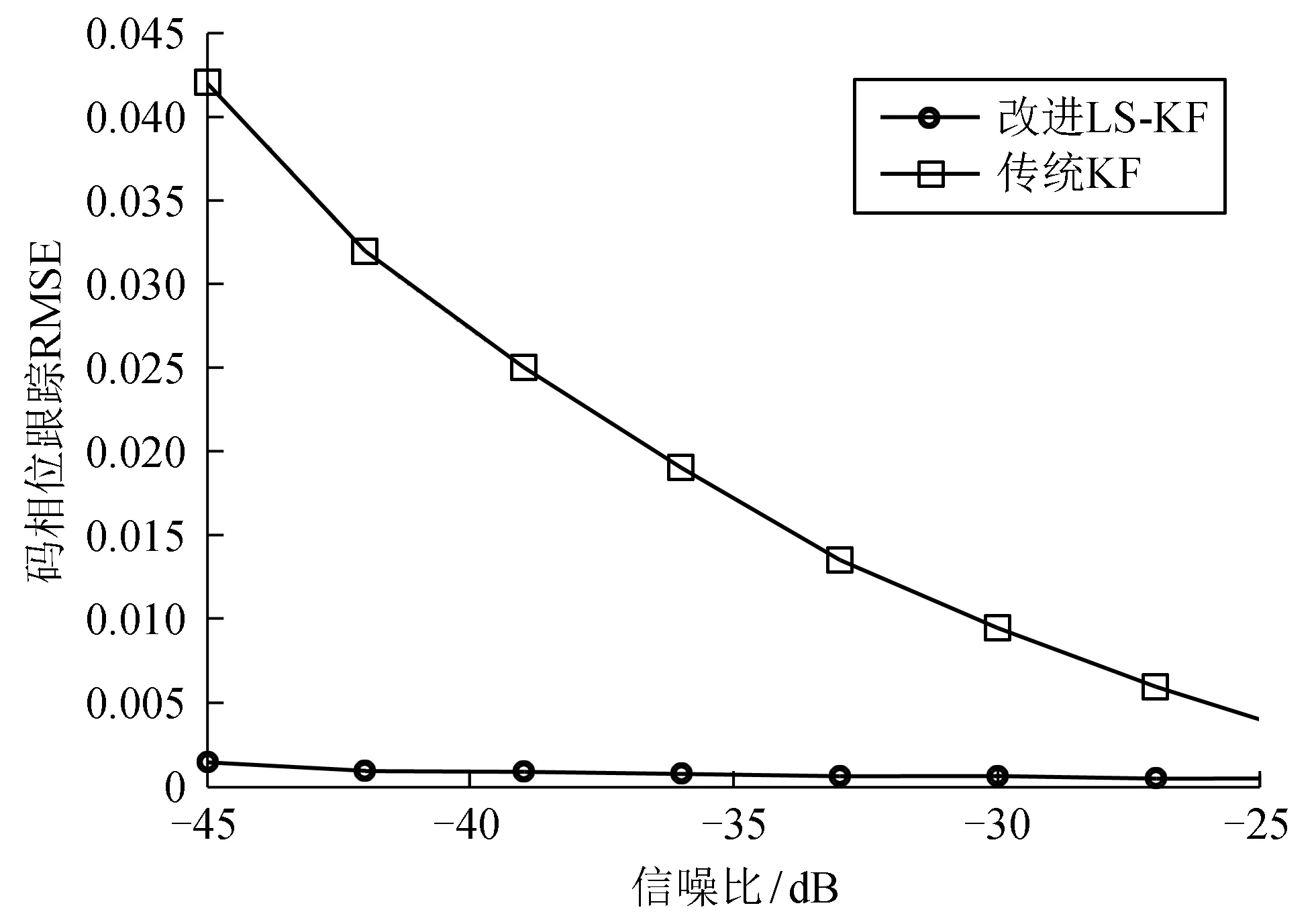
圖4 2種算法在不同信噪比下的碼相位跟蹤RMSE對比

為了進一步分析2種算法在不同多徑時延下的性能，仿真的2路信號中，多徑信號相對直達信號的幅度為1/2。圖5為2種算法在信噪比-45 dB和-25 dB時不同多徑時延下的碼相位RMSE跟蹤誤差。從圖5可看出，在多徑時延相同信噪比條件下，改進卡爾曼濾波算法比傳統卡爾曼濾波算法[10]的碼相位RMSE更小。改進卡爾曼濾波算法比傳統卡爾曼濾波算法具有更優的跟蹤性能。

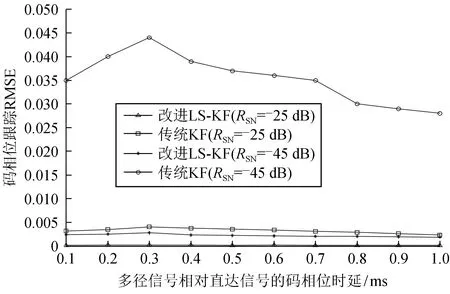
圖5 2種算法在不同多徑時延下碼相位RMSE對比

5 結束語

為了解決卡爾曼濾波處理伴有多徑干擾的微弱衛星導航信號的碼跟蹤時相干積分值組成的觀測量誤差較大的問題，利用最小二乘算法對相關函數因子進行修正的思想，構造一組無偏、均方誤差和最小的修正觀測值，建立數學模型，通過卡爾曼濾波得到更優的碼跟蹤性能，減小了相干積分中包含的多種誤差，且采用線性卡爾曼濾波器，具有計算量小的特點。本算法加入了發散判斷控制模塊，控制了卡爾曼濾波器的發散。仿真結果表明，與文獻[10]的算法相比，本算法對碼相位跟蹤具有更高的精度，特別是在低信噪比條件下，本算法的碼相位跟蹤誤差精度與強信號條件保持在同一個數量級,同時具有更穩定的跟蹤性能。在多徑時延變化的統計意義上，本算法的碼相位RMSE跟蹤誤差更小，具有更優的跟蹤性能。