仿人機器人協調阻抗控制算法

齊春麗， 伍錫如

(桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004)

近年來，仿人雙臂機器人在操作空間內具有優越的協調操作能力，可以完成重型物體搬運、零件裝配、焊接等復雜任務，已成為機器人領域的研究熱點。自20世紀80年代起，國內外許多研究者開始了對雙臂協作的研究[1-2]。

基于機械臂運動學和動力學模型，雙機械臂協作的諸多控制算法被提出，主要包括位置控制、力/位混合控制、阻抗控制等[3]。李賀立等[4]提出了一種新型阻抗控制算法，將雙臂看作主從臂，引入雙臂間相對誤差和虛擬恢復力概念，合理分配載荷，實現了雙臂用于搬運柔性物體的需求，同時減小了雙臂間誤差，提高了系統的穩定性。Caccavale等[5]提出基于阻抗內環和阻抗外環相統一的整體控制算法，解決雙臂的協調阻抗控制問題，并采用工業機器人進行實驗驗證，證明算法既能減小內應力，又能防止滑環現象的發生，克服了單一阻抗控制存在的缺點。敖天翔[6]將阻抗模型拓展為多點阻抗模型，并利用有限元理論對其求解，解決了雙臂協調操作過程中運動與力協調的分配問題，實現操作系統的可靠性。Tao等[7]提出了位置控制模型和力控制模型2種控制方案，將二者應用于協作機器人同一相互作用方向上，并驗證了控制方案的優越性。華磊等[8]提出一種擴展的冗余機械臂阻抗控制算法，該算法通過對操作空間和零空間共組的增廣操作空間解耦，得出相應驅動力矩，并引入避關節極限性能指標函數來優化零空間運動，確保冗余關節運動角度的合理性。陳鋼等[9]在雙臂協調操作運動約束關系的基礎上，提出了適用于協調操作的力/位混合控制方法，并通過實驗與傳統控制方法比較，驗證了該方法的正確性。Duan Jinjun等[10]針對雙臂協同時外部干擾和校準誤差會引起未知軌跡偏差的問題，提出了一種用于力/位跟蹤的對稱自適應變導納控制方法，該方法能夠補償偏差，減小其對系統的影響。

考慮到操作過程中干涉力會對雙臂產生影響，許多研究者通過引入擾動觀測器，以控制干涉力對雙臂的影響。司彥娜等[11]采用非線性干擾觀測器的自適應反演滑模控制方法，實現對機械臂軌跡跟蹤問題的控制，保證系統穩定性。Sadeghian等[12]基于任務空間誤差和機器人的廣義動量，設計了2種不同的擾動觀測器，以觀測估計和補償任務變量上的廣義力，確保任務空間誤差的漸近穩定性，并在七自由度機械臂上進行了實驗驗證。錢琮瑋等[13]基于動量守恒設計了一種外部擾動觀測器對機械臂碰撞的作用力進行預估，根據觀測器觀測結果的不同設計相應的響應控制方法，避免機械臂與機械臂和機械臂與外部干擾的碰撞。

為了實現既能觀測對外部擾動，又可達到合理分配載荷的目的，保證物體搬運過程中的控制精度，考慮到操作物的運動特性，構建統一動力學模型，結合基于廣義動量的擾動觀測器觀測外部擾動力矩，設計了適用于雙臂協調的阻抗控制方法，同時引入變加權矩陣以求得最優抓取矩陣，達到協調操作過程中合理分配載荷的目的，提高操作系統的性能。

1 仿人機器人運動學模型

1.1 正逆運動學分析

多關節機器人是由多個連桿組成，各連桿之間通過相鄰坐標的齊次變換(平移變換和旋轉變換)實現機械臂末端位姿變換，完成預定工作。相鄰坐標之間的變換通式為

(1)

其中qi、ai-1、αi-1、di為機械臂連桿相對應的D-H參數，分別表示各關節轉角、連桿長度、相鄰關節的扭轉角、連桿偏移。根據D-H參數法可得2個七自由度機械臂末端相對于基座坐標系的位姿變換矩陣為

(2)

若已知機械臂末端位姿，求解機械臂各關節的轉角變量的過程稱為機械臂的逆運動學分析，逆運動學是正運動學的逆運算。

1.2 雙臂運動學模型

采用n(n=7)自由度的Baxter仿人雙臂機器人，其模型如圖1所示，相應的關節空間動力學模型為

(3)

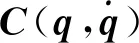
圖1 雙臂機器人模型

由于外力矩由機械臂末端受外力所產生的操作力矩分量μo和其他位置的擾動力矩分量μd組成，式(3)可改寫為

(4)

通常，機械臂末端操作空間和關節空間的轉換關系為

(5)

其中：x為機械臂末端位姿；J為雅可比矩陣。式(5)的另一種形式為

(6)

其中：J+為雅可比矩陣的廣義逆矩陣；δ為任意n維向量。式(6)中前后兩部分分別表示機械臂操作空間和零空間的運動動力學模型。

設零空間速度向量為v，雅可比矩陣為JN，兩變量約束條件為

(7)

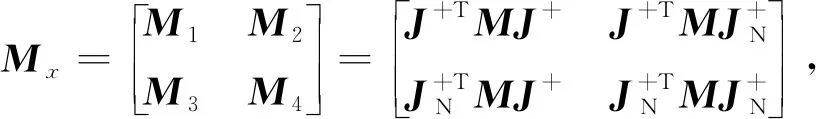
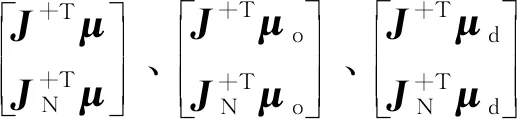
1.3 雙臂與操作物統一動力學模型

仿人機器人緊協調時雙臂與操作物之間的約束及受力關系如圖2所示。其中：Ol和Or分別為左右臂在操作物上的抓取點；Oc為操作物質心；Of為仿人機器人基座坐標原點；ftl、ftr、τtl和τtr分別為雙臂末端輸出力和左右臂輸出力矩；m0g表示操作物體的重力。

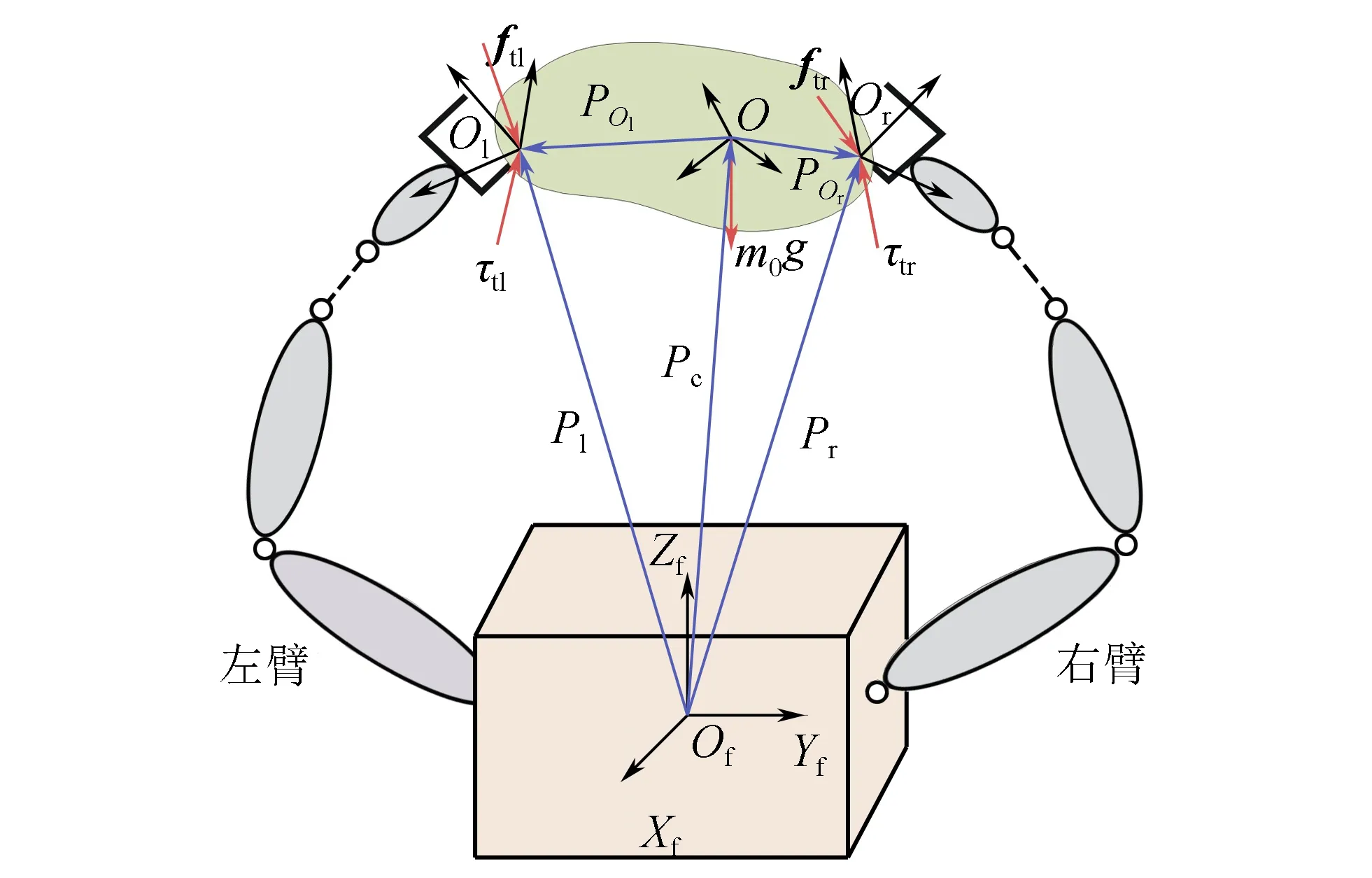
圖2 仿人機器人緊協調操作約束及受力關系

根據緊協調操作特性，當忽略操作物形變時，O、Ol和Or處的速度、加速度均相等。操作物質心處所受合力表達式為

(8)

由牛頓-歐拉方程，操作物動力學方程為：

(9)

其中：Io為操作物慣性矩陣；ωo為操作物角速度。由式(8)、(9)可變換為

(10)

其中：W為雙臂協調操作是的抓取矩陣；Mo為常數矩陣；Co為反對稱矩陣。

根據式(10)，雙臂作用在操作物質心的操作力為

Ft=W+(Fo-Fto)+(I12-W+W)Ωd=

(11)

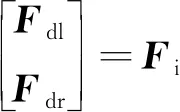
(12)

用Ft代替式(7)中的J+Tμo，在滿足雙臂緊協調操作特性的基礎上，仿人雙臂機器人與操作物的統一動力學模型為

(13)

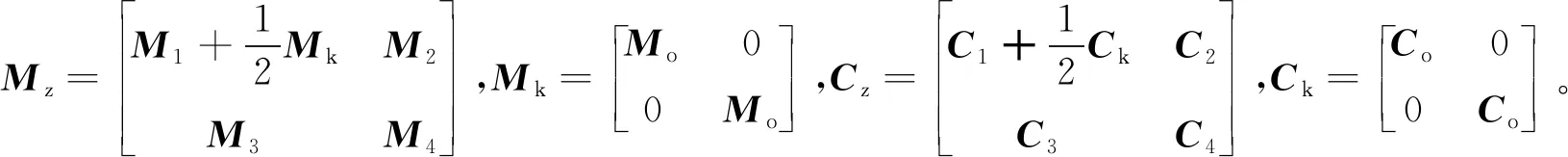
2 帶有擾動觀測器的雙臂阻抗控制

2.1 雙臂阻抗控制

阻抗控制可以很好地控制機械臂和環境之間的相互作用，能夠實現機械臂協調操作的穩定性。冗余雙臂關節空間阻抗方程式為

(14)

其中：qd為機械臂的期望軌跡；Md、Bd和Kd分別為關節期望慣性、期望阻尼和期望剛度。式(14)的對應控制輸入為

(15)

采用期望內力Fid和調節系數L實現操作物內力平滑變化。為控制操作物內力，設操作物期望位姿為xd，根據式(13)，機械臂操作空間阻抗方程為：

(16)

其中：Mx、Bx和Kx分別為操作物期望慣性、期望阻尼和期望剛度。式(16)相應的控制輸入為

Kx(xd-xo)]。

(17)

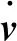
(18)

根據式(18)，可知零空間的阻抗方程為

(19)

其中Mv、Bv和Kv分別為零空間中期望慣性、期望阻尼和期望剛度。由于零空間位置誤差不易定義，由文獻[14]可知，經投影的關節空間誤差能被用來定義零空間所要求的輸入加速度，

(20)

2.2 基于廣義動量的擾動觀測器

未知環境對機械臂產生的外部擾動干涉力對機械臂運行的軌跡精度有很大的影響，為了提高機械臂運動精度，增加機械臂穩定性，設計了基于廣義動量的能觀測擾動干涉力矩μd的控制器。

根據統一動力學模型(13)，定義機械臂的廣義動量為

(21)

則

(22)

令殘余向量r作為觀測器指標，其表達式為

(23)

則

(24)

其中Kr為正定對角線矩陣。特別地，P(0)=0，r(0)=0。

當存在干涉力時，觀測器指標會快速增加到-μd，根據外力矩的變化而變化，實現對干涉力矩的觀測。結合式(23)和式(17)，用殘余向量代替擾動力矩μd，式(17)可改寫為

Kx(xd-xo)]。

(25)

(26)

該控制律能控制操作物運動和內力分配，解決因干涉力導致的機械臂運行精度下降問題，保證緊協調操作過程中機械臂及操作物的穩定運行。

設計合理的抓取矩陣，可直接控制分配載荷及內應力的大小。定義W+為

(27)

機械臂在緊協調搬運時的總驅動能量為

ξ=0.5μTμ。

(28)

若要合理分配抓取載荷，則需要對式(28)進行最小優化處理。采用KKT條件對其進行最優化[15]，引入變加權矩陣實現了抓取載荷的合理分配，且能控制操作物內應力的大小，使操作系統性能達到最優。

3 實驗結果與分析

為了驗證本算法的正確性，采用七自由度的雙臂機器人為模型，利用Matlab軟件平臺進行仿真實驗。表1為其中一個機械臂的D-H參數。

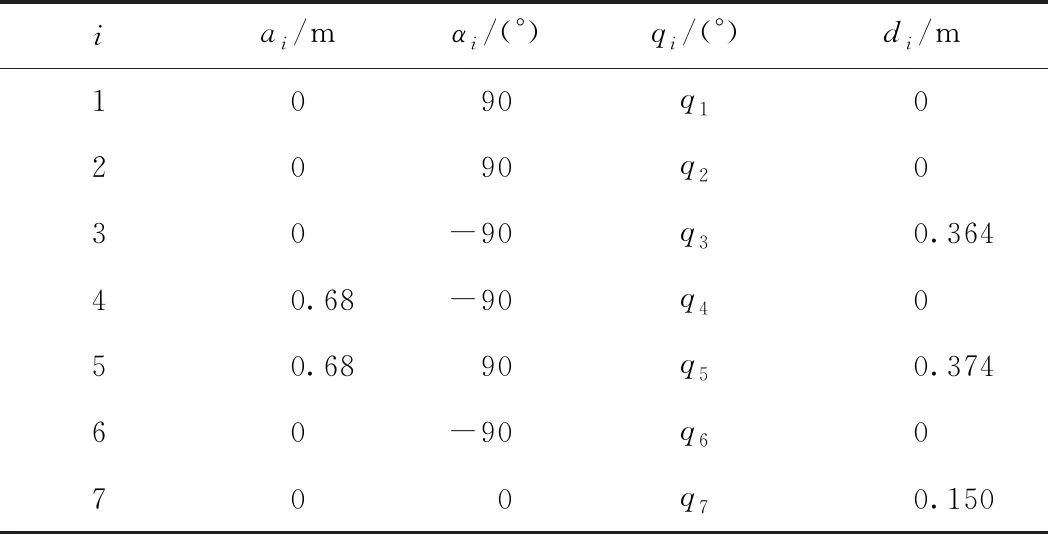
表1 雙臂D-H參數表

仿真時將2個機械臂的初始關節角分別設置為ql=[-π/20π/6π/2-π/1.4π0]和qr=-ql，機械臂的終止關節角度為ql=[-ππ/2π/2π/3.5-π/60π/8]，操作物體的質量為4 kg，操作時間為40 s，時間間隔為0.05 s，阻抗控制參數分別為Bx=16E6，Kx=0.2E6，Bv=1.5E14，Kv=16E14。

圖3為無觀測器時操作物體的位置誤差。從圖3可看出，當無觀測器時，操作物體的位置誤差比較大。圖4為有觀測器時操作物體的位置誤差。比較圖4、圖3可看出，引入觀測器后，操作物體的位置誤差遠遠小于無觀測器的位置誤差，表明操作物體位置精度有很明顯的提高。

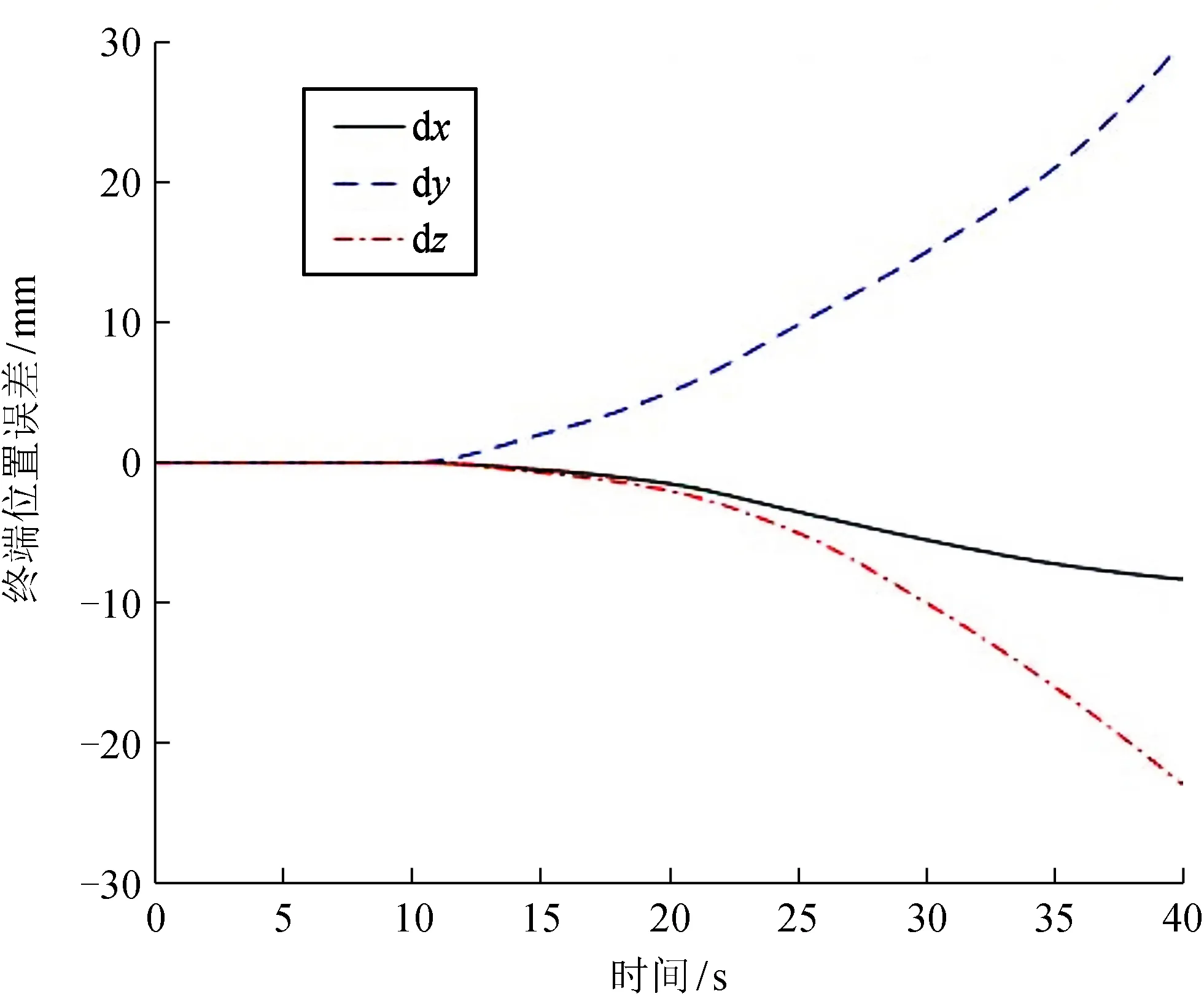
圖3 無觀測器時操作物體的位置誤差

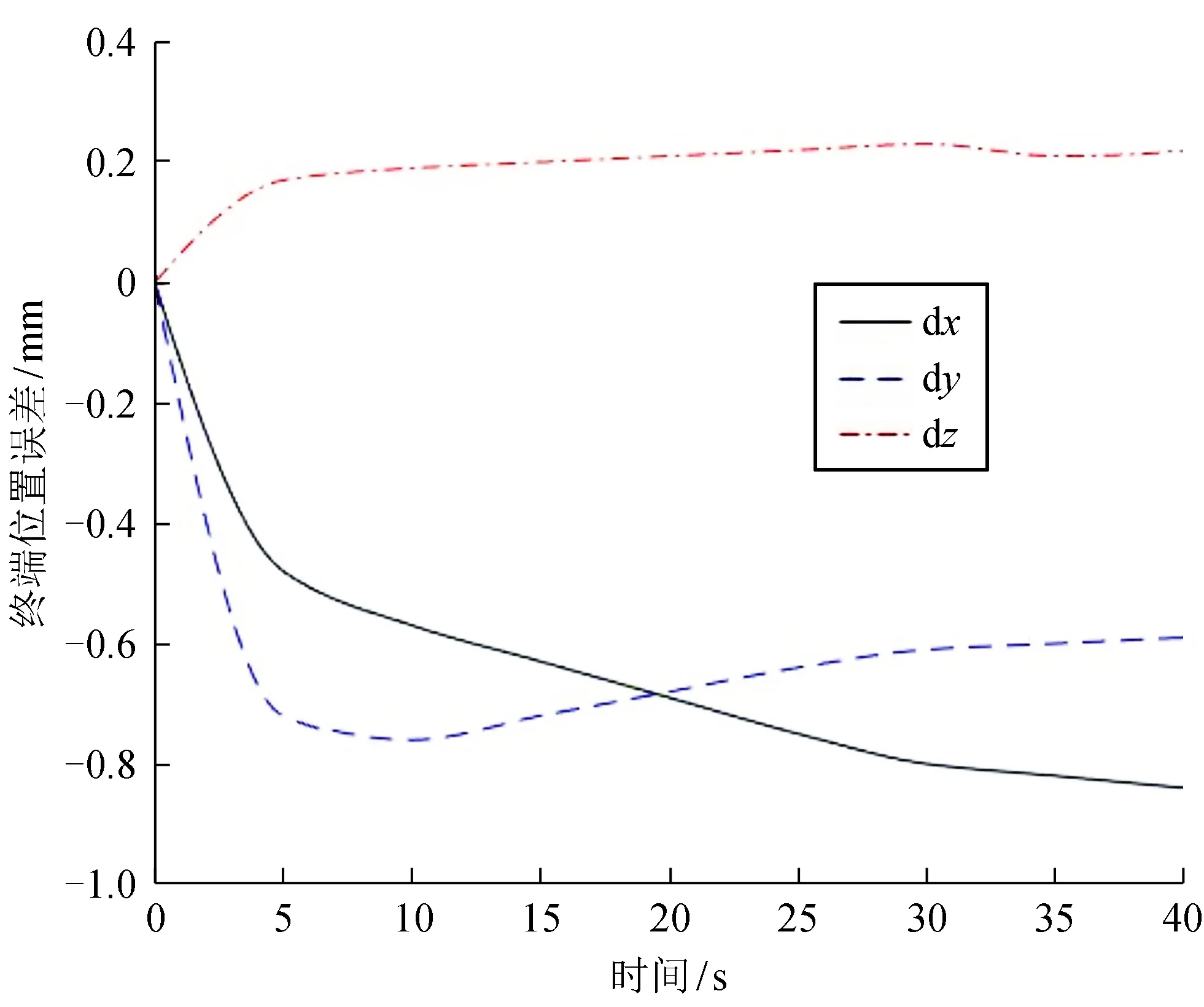
圖4 有觀測器時操作物體的位置誤差

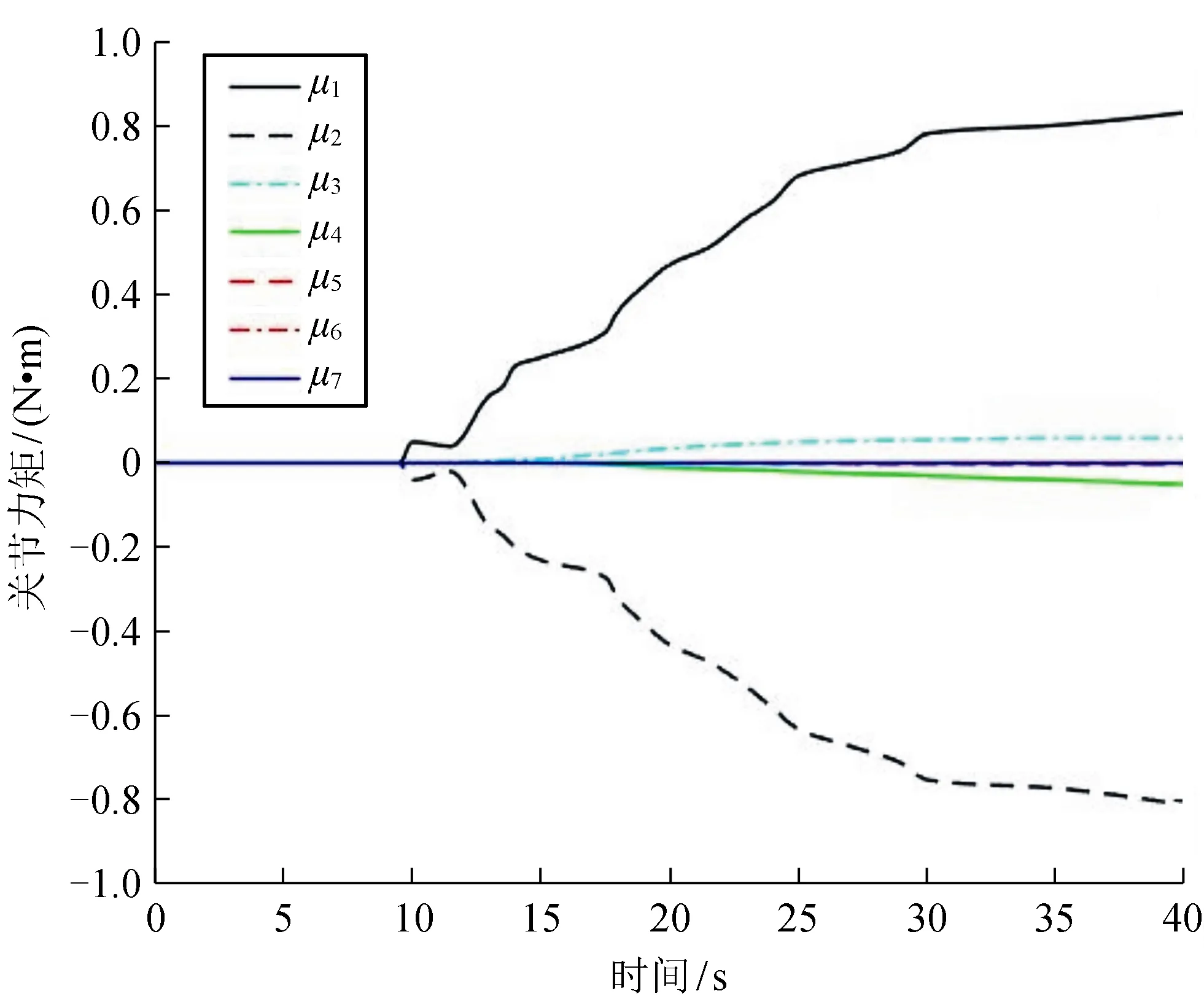
圖5 機械臂的實際關節力矩

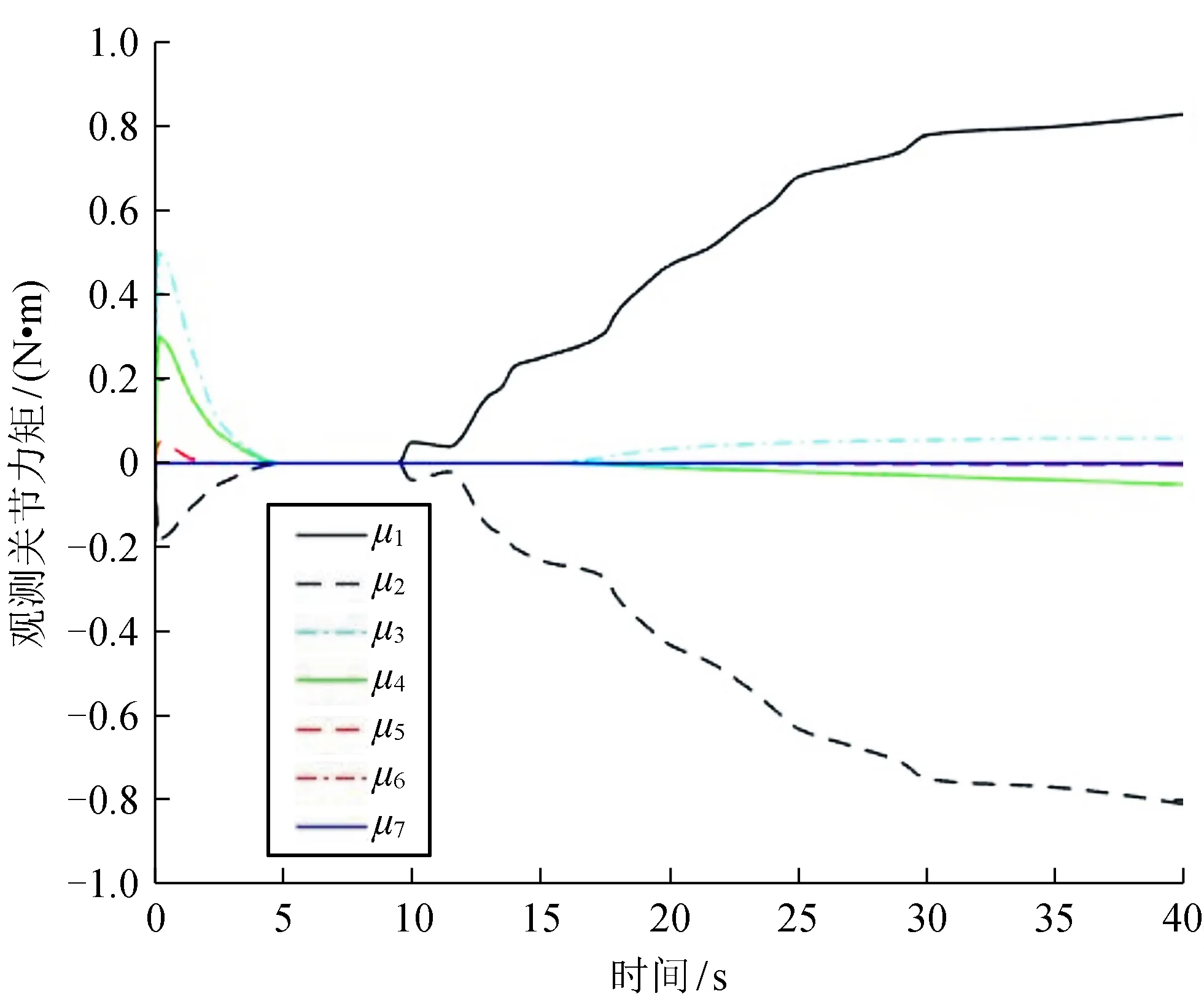
圖6 觀測器觀測的關節力矩

圖5為機械臂的實際關節力矩，圖6為觀測器觀測出的關節力矩。對比圖5、6可看出，10 s時存在外干涉力條件下，觀測器觀測的關節力矩與實際關節力矩基本一致，說明了本觀測器是有效的。

4 結束語

針對仿人雙臂機器人在未知環境下協調操作時操作物和機械臂軌跡跟蹤精度低的問題，在阻抗控制方法的基礎上，提出了雙臂緊協調的控制算法。通過分析緊協調操作時物體與雙臂存在的約束關系，建立兩者統一動力學模型。同時，為了使機械臂達到節約工作資源、優化分配載荷的目的，引入變加權矩陣。為了能實現對未知環境干涉力的直接控制，采用能觀測外部干涉力的擾動觀測器，使其與阻抗控制模型結合，設計了仿人雙臂機器人的協調阻抗控制算法，提高了操作物的位置跟蹤精度，極大地改善了協調操作的性能。