考慮自由液面波形的艦船水下輻射噪聲計算方法
李 清,楊德慶,于 漢
(上海交通大學a.海洋工程國家重點實驗室;b.高新船舶與深海開發裝備協同創新中心,上海200240)
0 引 言
艦艇水下輻射噪聲以聲源級表征艦船的聲隱蔽性,主要由機械噪聲、螺旋槳噪聲及水動力噪聲構成[1]。艦艇機械噪聲包括主機、輔機、泵系等引起的振動輻射噪聲以及螺旋槳軸承力和表面力激勵引起軸系振動和結構振動產生的輻射噪聲,構成了艦艇水下輻射噪聲的低頻離散線譜,艦艇水下輻射噪聲一般特指艦船機械噪聲。
針對機械噪聲,楊德慶等[2]利用有限元/邊界元方法計算了某艦艇近場輻射噪聲與自噪聲特性;Zheng等[3]采用FEM-BEM 計算了柴油機激勵導致的船體結構振動及其水下聲輻射;付建等[4]計算了螺旋槳激振引起的船體結構振動與輻射噪聲;李清等[5]歸納出求解艦船水下輻射噪聲的兩種模式及四種數值計算方法。以上文獻中在求解水面艦船機械噪聲時,均假定艦船與流體絕對靜止,把自由液面邊界作為平面計算艦艇水下聲輻射,這種處理方式在國內工程實踐中亦廣泛多見。關于自由液面,黎勝等[6]研究了自由液面對脈動球輻射聲功率和輻射指向性的影響;鄒元杰等[7]探討了自由液面和剛性壁面對結構振動與聲輻射的影響;鄒明松等[8]提出了帶航速和考慮自由液面的聲介質中三維水彈性結構聲輻射計算方法,并以帶航速的浸水彈性球殼為例,結合實驗驗證了算法的正確性。以上文獻亦將自由液面作為絕對平面展開理論研究,指出自由液面對聲輻射以及結構振動特性均有重要影響。然而,在目前公開發表的文獻中,考慮自由液面形狀的水面艦船水下輻射噪聲計算方法的研究非常少。當求解航行狀態下水面艦船輻射噪聲時,自由液面處的聲學邊界已不再是平面,聲學計算精度此時依賴于艦船航行的流場計算和聲學邊界處理。因此,探索考慮自由液面波形的水面艦船水下輻射噪聲計算方法,探討自由液面波形對輻射噪聲計算精度的影響程度,對于提高水面艦船輻射噪聲的計算精度具有參考價值。
本研究針對基于Wigley數學船型設計的某護衛艦,采用URANS方法基于SST k-ω湍流模型,數值計算Wigley 護衛艦在靜水中勻速航行時的繞流流場,導出興波波形作為聲學計算時自由液面處的邊界條件。應用聲學有限元自動匹配層(FEM-AML)方法,采用聲固耦合模式,建立了自由液面分別為波面與平面兩種聲學數值分析模型,計算了兩種聲學邊界條件下的水下輻射噪聲,比較了在兩種聲學模型下輻射聲壓分布、輻射聲功率以及船體聲振耦合響應,探討了自由液面波形對水下輻射噪聲計算精度的影響,為水下輻射噪聲的精細化計算提供參考。
1 水面艦船流場及其水下輻射噪聲計算理論
1.1 RANS方法與SST k-ω模型
采用基于RANS 控制方程的SST k-ω 湍流模型計算水面艦船繞流流場,SST k-ω 模型在近壁面處采用k-ω 模型,遠處自由剪切流動采用k-ε模型,由于模型考慮了剪切力的影響,因此能夠比較好地模擬強逆壓梯度的流場。SST k-ω模型中湍流動能k,湍流耗散率ω及渦黏性系數νt滿足下面方程[9]
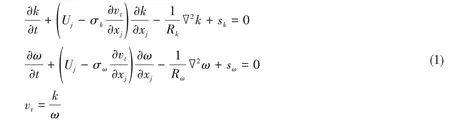
式中,有效Reynolds數及湍流產生項Rω定義如下:

k和ω方程的源項sk和sω如下:
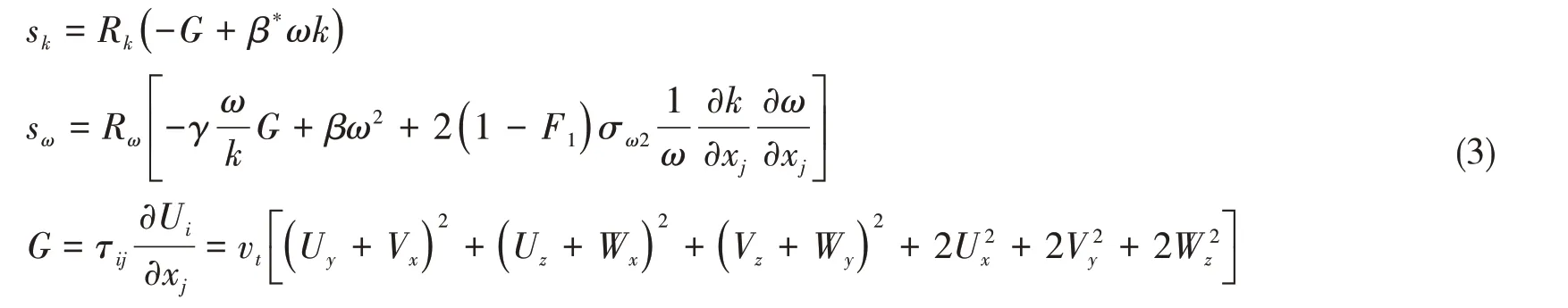
以上各式中:β*、β、σk、σω和γ 均為Blended k-ω/k-ε 模型常量,F1為混合函數,表達k-ω/k-ε 模型混合使用情況。
1.2 自由液面的數值模擬
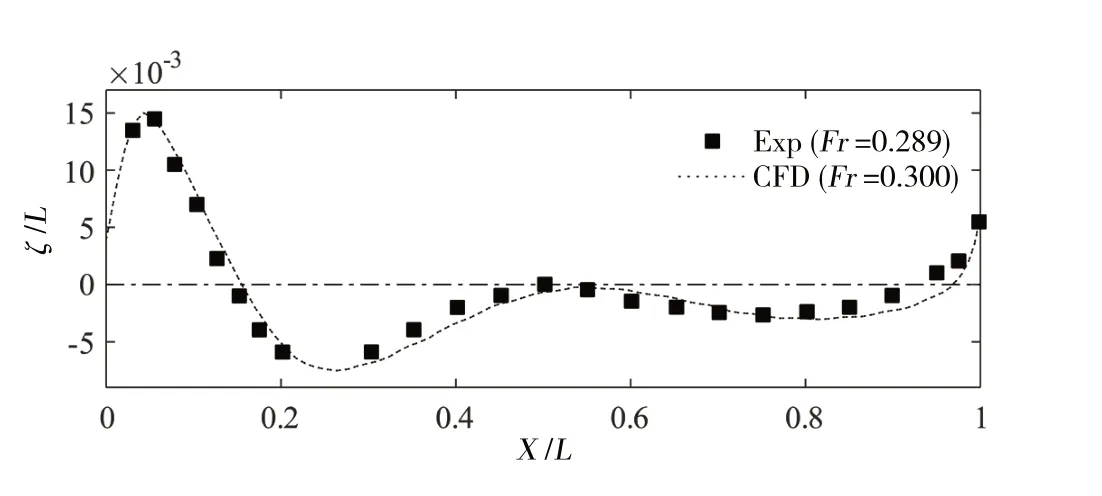
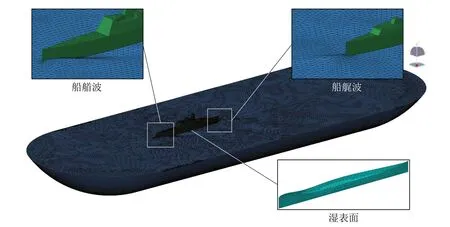
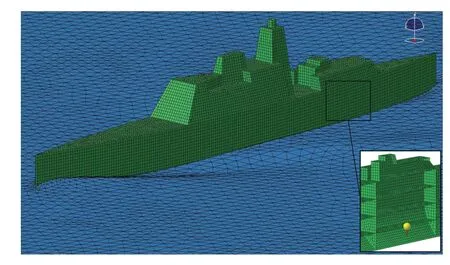
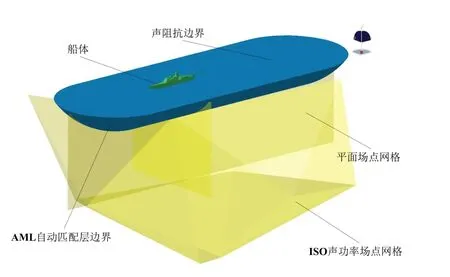
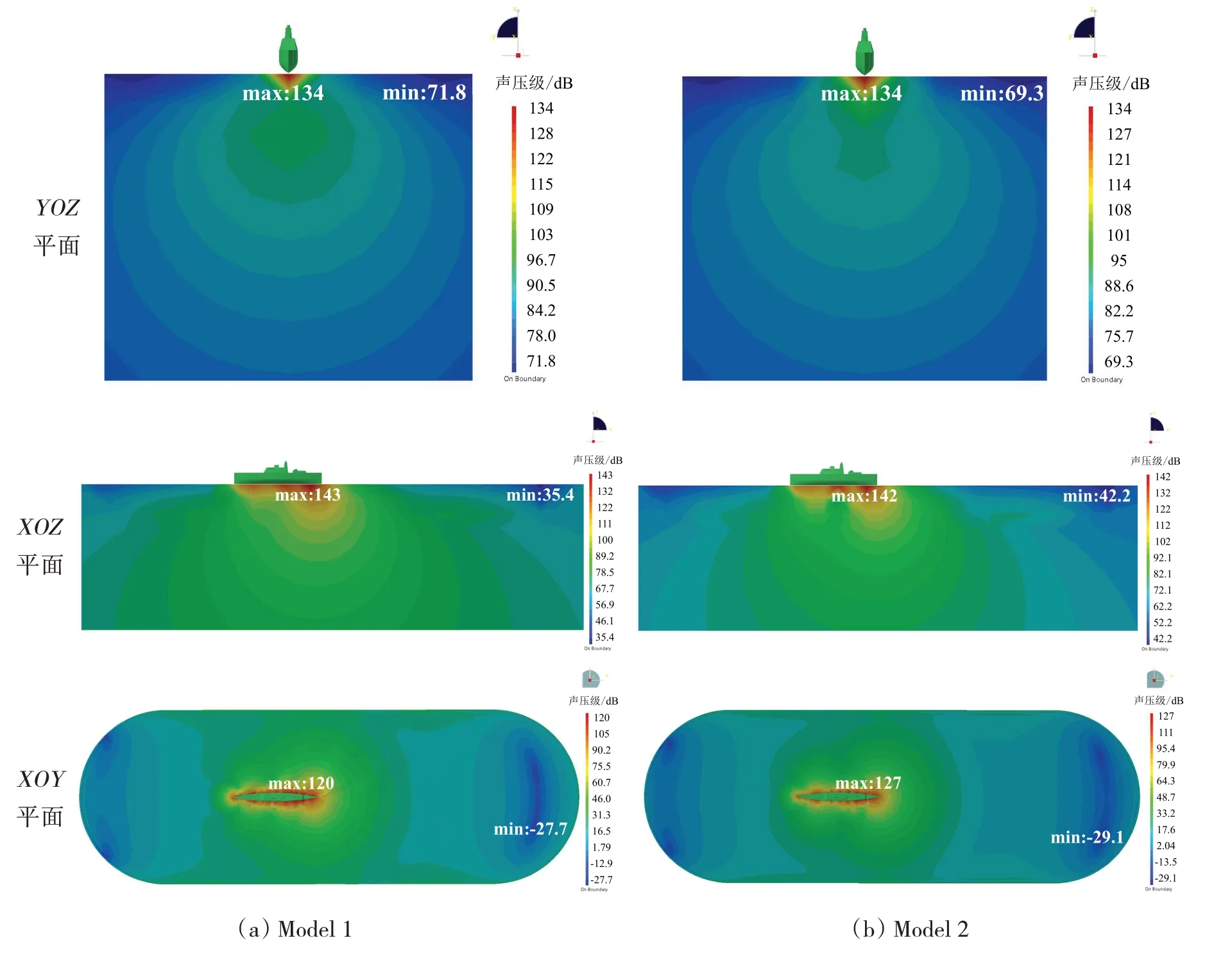
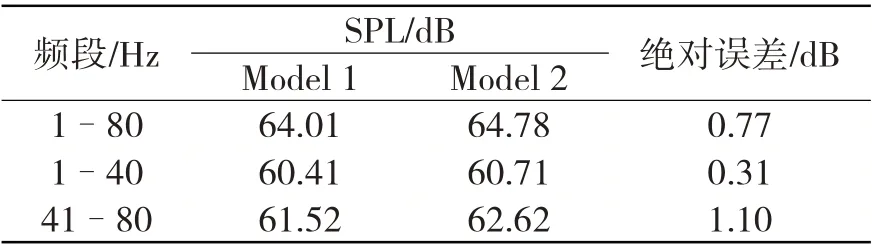
流體體積法VOF(Volume of Fluid)通過定義流體體積函數F 來標識每個網格單元狀態,F 等于單元內流體體積與該單元體積之比。若F=1,則單元全部為制定相流所占據;若F=0,則單元為無制定相流體單元;若0 聲波在兩種媒質分界面處會發生反射與折射,其大小取決于兩種媒質的特性阻抗。介質的聲特性阻抗定義為介質中某點的有效聲壓與通過該點的有效質點速度的比值,亦可表示為介質密度ρa與聲傳播速度ca的乘積 基于聲學有限元法計算艦船水下輻射噪聲時,需在自由液面處賦空氣特性阻抗以模擬阻抗邊界條件[10]。 海水為重密度媒質,艦船振動輻射噪聲計算必須考慮船體結構和流體的聲振強耦合作用,結構和聲學響應需同步耦合計算。理想均勻流中的聲學基本方程為波動方程,對結構力場、聲場進行離散推導得到的結構有限元耦合聲學有限元的聲固耦合動力學方程為[11] 本研究所用護衛艦簡化模型在Wigley數學船型 基礎上補充上層建筑及基本結構而成,式中各參數具體數值見表1。 表1 Wigley數學船型主要參數Tab.1 Main parameters of the Wigley hull Wigley 護衛艦結構模型主要包括6 層甲板、6 個縱艙壁等主要板結構,并由橫梁、縱骨等主要梁結構加強,板結構用Shell單元模擬,梁結構用Beam 單元模擬。使數值船模固有特性符合實船模態分布,材料楊氏模量取E =40 MPa,密度ρs=7 850 kg/m3,泊松比μ = 0.3。Shell單元厚度均為10 mm,Beam 單元均為25×5 mm2矩形截面。護衛艦結構有限元模型(圖1)網格尺寸需根據薄板橫向振動彎曲波理論確定 式中:λs為薄板中彈性彎曲波波長,h 為最小板厚,fmax為分析頻段最大頻率。本研究計算頻段為1-80 Hz,按上式計算得到λs=130.3 mm。為滿足振動計算網格劃分精度要求,本模型網格尺寸取為15 mm。本模型節點數為28 851,Shell 單元數為28 990,Beam 單元數為1 474。Wigley 護衛艦一階水平彎曲振動、一階垂向彎曲振動以及一階扭轉振動(圖2)的固有頻率分別為2.989 Hz、3.442 Hz和7.718 Hz。 圖1 Wigley艦結構有限元模型Fig.1 Structural finite element model of theWigley frigate model 圖2 Wigley艦總體振動特性Fig.2 Overall vibration characteristics of the Wigley frigate model 采用模態疊加法計算聲振響應,參與計算模態基對應的最大頻率一般取到計算頻率的兩倍以保證計算精度。故取本船前2 154 階模態,第2 154 階固有頻率已經達到160 Hz(160.069 Hz),則本研究采用模態疊加法進行結構-聲耦合計算,其結構模型可滿足精度要求。以上計算了船體干模態,若采用船體濕模態進行聲固耦合分析,將重復考慮結構與流體介質間的相互影響,計算結果會產生偏差[5]。 以Stoep[12]實驗為參照,對Wigley 艦在靜水中勻速航行的繞流流場進行數值模擬。本研究計算船模航行速度(來流速度)為1.627 m/s,船模航行弗勞德數Fr = 0.3,雷諾數Re = 5×106。 坐標系同圖1,流體流向為x正向,重力方向為z負向。取入口距船艏0.75倍船長,出口距船艉2倍船長,側面和底面距船體1倍船長,整個流場計算域為長方體;船體表面為無滑移邊界條件,入口和出口分別為速度入口和壓力出口邊界,遠場邊界設置為對稱邊界條件(圖3)。采用結構化網格(圖4),船艏、船艉及水線面附近處流場變化較劇烈需進行局部加密,船體表面邊界層根據y+= 30 計算得到的第一層網格厚度進行加密,網格總數約400萬。 來流馬赫數為0.1%,按不可壓縮流動求解。基于壓力求解器,時間類型為瞬態,采用URANS 方法,湍流模型為SST k-ω模型,多相流模型為VOF模型。當總阻力系數和自由面波高收斂,流場趨于穩定時,停止流場計算。由于艦船在靜水中勻速航行興波定常,在流場穩定后其自由液面不再變化,故取流體體積函數F = 0.5的等值面(自由液面)導出,作為后續聲學計算的邊界條件。 圖3 Wigley船流場計算域及邊界條件 Fig.3 Flow domain and boundary conditions of the Wigley hull 圖4 Wigley船流場計算結構化網格劃分Fig.4 Structured mesh for the flow domain of the Wigley hull 船舶總阻力Rt分為摩擦阻力Rf、興波阻力Rw和粘壓阻力Rpv,后兩者共同構成剩余阻力Rr。本文計算得到的各項阻力系數與Stoep[12]實驗結果(Fr = 0.3)比較見表2,其總阻力系數相對于實驗值誤差小于1%,剩余阻力系數與摩擦阻力系數與實驗值也較接近;船體表面波高(圖5)計算結果與Kajitani 等人[13]實驗結果(Fr = 0.289)比較如圖6,波高沿船長分布亦與實驗值吻合良好。由于弗勞德數(Fr)不完全一致,波形主要于船艉處存在一定的差別。通過與相關實驗對比,從阻力系數與自由面波高分布兩方面驗證了流場數值計算結果的可靠性。 表2 阻力系數與Stoep[12]實驗結果比較Tab.2 Resistance coefficients compared with Stoep[12]experiment results 圖5 XY平面自由液面波高分布 Fig.5 Free surface wave height distributions of the XY plane 圖6 XZ平面船體表面波高與Kajitani等人[13]實驗結果比較Fig.6 Hull surface wave height of the XZ plane compared with Kajitani,et al[13]experiment results 求解艦船水下輻射機械噪聲時普遍假定艦船與流體均為靜止,把自由液面邊界視作不考慮波形的平面[5]。實際情況是航行中船體浸潤區域時刻變化,自由液面處的聲學邊界應當考慮波面形狀。因此,求解非定常流動中的艦船輻射噪聲,其計算精度一定與自由液面流場形狀和聲學邊界處理方法有關。當需要嚴格考慮自由液面波形時,因通過反對稱平面構建自由液面的聲學邊界元法[10]已經失效,必須采用聲學有限元法。為探索考慮自由液面波形的水面艦船水下輻射噪聲計算方法,本研究建立的自由液面邊界分別為波面和平面的兩種(圖7)聲學數值模型,采用聲學有限元自動匹配層(FEM–AML)方法計算Wigley艦水下輻射噪聲,并探討自由液面波形對輻射噪聲計算精度的影響。 圖7 Wigley艦兩種自由液面聲學幾何模型Fig.7 Two Acoustic free surface geometry models of the Wigley frigate Wigley 艦水下輻射機械噪聲計算頻段為1-80 Hz,采用聲固耦合分析模式[5]。設定聲學有限元環境,為細致描述自由液面波形分布特征,聲學單元特征長度取0.1 m,總單元數約為230 萬。聲學單元模擬海水,密度ρa=1 025 kg/m3,聲波傳播速度ca=1 480 m/s。根據聲波理論,80 Hz 聲波波長λa=ca/fmax=18.5 m,聲學單元尺度遠滿足計算頻段最小波長內至少有6個單元的精度要求。圖8為聲固耦合水下輻射噪聲計算模型。在船體機艙板架處施加垂向激振力Fz=1 N(圖9),導入2.1節中船體干模態,船體濕表面(圖8)為結構-聲學耦合面,取頻段內結構模態阻尼系數為1%,進行結構-聲耦合同步計算遠場聲輻射。平面自由液面模型與上述類似。 在自由液面對應的網格處設置阻抗邊界條件,賦空氣特性阻抗Zp=416.5 kg/(m2·s),聲場中表征遠場邊界的表面賦AML 聲吸收邊界條件(圖10)。根據護衛艦主尺度,建立水下長17.25 m、深5 m 的平面場點以觀測輻射聲壓分布,同時設置標準聲功率球面場點以評估遠場輻射噪聲。平面自由液面模型亦與上述類似處理。 圖8 Wigley艦水下輻射噪聲聲固耦合計算模型Fig.8 The vibro-acoustic model of the Wigley frigate for underwater radiated noise 圖9 機械噪聲激振力加載 Fig.9 The excited force for mechanical noise 圖10 聲學邊界條件與場點設置Fig.10 Acousticboundaryconditionsandthefieldpointsetting 本研究計算了Wigley艦低頻1-80 Hz的機械噪聲聲功率譜級,并通過平面場點觀測水下輻射噪聲分布及指向特性(圖11)。船體機艙底部板架激振力激起對應頻率點附近的船體模態,并導致船體結構振動,船體外板產生振動響應。依賴于速度連續邊界條件,船體結構浸水外板向流體質點傳遞振動能量,船體由艦艏至艦艉一并向水下輻射聲波,而能量大部分還是集中在艦艇機艙附近,艇體可視為線聲源,流體亦產生聲振耦合反作用影響船體結構振動,輻射噪聲遠場聲壓基本上隨輻射半徑增大而逐漸遞減。采用自由液面分別為波面和平面的聲場模型求解的聲場分布特征以及輻射聲壓最值(Ref.1 μPa),均存在一定程度上的差異。 圖11 Wigley艦機械噪聲輻射聲壓分布(50 Hz)Fig.11 Radiated sound pressure distribution for mechanical noise of the Wigley frigate(50 Hz) 圖12 為Wigley 艦聲振耦合位移頻率響應,兩種聲學模型對結構振動響應亦有一定程度上的影響。圖13 為機械噪聲遠場輻射聲功率譜級(Ref.1×10-12W)。根據圖13 和表3 可知,兩種自由液面聲學模型計算所得輻射聲功率頻譜與其總聲功率級均存在差異,兩種模型的計算偏差為0.77 dB(約0.8 dB)。其主要原因是對于波形曲面與絕對平面兩種自由液面模型,邊界幾何形狀的不同導致了聲輻射邊界條件不同,結構-聲耦合面(艦船濕表面)的幾何形狀亦有差異,從而使計算結果產生差別。表3 分別計算了1-40 Hz 及41-80 Hz兩個頻段內總輻射聲級,兩種模型絕對誤差分別為0.31 dB 和1.10 dB,且隨頻率的增加而增大。圖13亦表明,兩種聲學模型聲功率線譜在較低頻段基本吻合,而隨著頻率增大偏差愈明顯。 綜上,兩種自由液面聲學模型計算效率與計算規模基本相當,嚴格考慮波形的自由液面聲學模型計算精度更高,且更加逼近真實物理環境。聲學模型建模精度對機械噪聲存在一定程度的影響,其影響程度隨頻率的增加而增大,自由液面為平面的聲學模型的計算結果偏大。 表3 兩種聲學模型合成聲功率級對比Tab.3 Comparison on overall SPLs of two vibroacoustic models 圖12 聲振耦合船體結構位移頻率響應(50 Hz)Fig.12 Vibroacoustic displacement responses of the frigate structure(50 Hz) 根據以上結論可以推測,若計算水面艦船水動力噪聲,自由液面波形對水動力噪聲的影響程度應大于機械噪聲。其原因在于:計算水動力噪聲時,除了兩種聲學模型自由液面處邊界條件、結構-聲耦合面幾何形狀的差異,實際上船體浸潤區域的不同亦會導致從流場映射到聲學網格上的脈動壓力(聲壓激勵)存在較大差別,甚至后者可能對最終結果起主導作用;且水動力噪聲是全頻段連續噪聲譜,中高頻的聲學計算更需要精確的聲學計算模型。另一方面,自由液面波形對計算精度的影響程度因船型而異,影響程度的大小需具體船型具體分析,本研究中Wigley 數學船模瘦長且流線型規則,興波現象并不明顯,因而兩種聲學模型計算差別并不算大(0.8 dB);且對于實際工程水面艦船的水下輻射噪聲計算,實船與模型間亦存在尺度效應,不可因本文研究結果之間的偏差較小而忽視自由液面波形對水面艦船水下輻射噪聲的實際影響,而應根據實際工程對計算精度的要求選擇合適的計算方法。最后,本研究模擬勻速航行水面艦船的靜水興波,流場穩定后自由液面不再隨時間變化(定常),故可直接采用文中聲場建模方法;而在模擬真實船舶航行時亦會存在隨機波浪、變航向、變航速等非定常因素,此時可同樣采用本文方法,將流場中各時刻對應的自由液面波形導出,分別建模計算各個指定時刻的水下輻射聲場,或者進一步探索時域的聲學計算模型。 以某Wigley艦為算例,綜合探索了考慮自由液面波形的水面艦船水下輻射噪聲的計算方法,探討了自由液面波形對艦船水下輻射噪聲計算精度的影響,為提高水面艦船輻射噪聲計算水平提供參考與建議。研究得到以下結論: (1)嚴格考慮波形的自由液面聲學模型計算精度更高,自由液面波形對艦船水下輻射噪聲有一定程度上的影響,其影響程度隨頻率的增大而增加,自由液面為平面的聲學模型的計算結果偏大。 (2)本研究數值模擬了艦船靜水興波勻速繞流的定常流場,自由液面波形是穩定的;若求解艦船在波浪中航行的非定常流場中的水下輻射噪聲,自由液面波形及船體浸水表面時刻變化,可針對不同時刻的自由液面形狀,分別建模計算水下輻射聲場,或進一步探索水面艦船時域水下聲輻射的計算模型與方法。 (3)采用基于URANS方法的SST k-ω湍流模型計算自由液面波形與實驗吻合良好;但若求解艦船水動力噪聲,由于固體壁面的偶極子聲源的大小和分布特性決定其外部輻射聲場的強弱及其分布規律,而URANS 方法針對艦船航行時的流動分離與尾渦計算存在明顯不足,此時必須采用LES 湍流模型,亟待后續探討。 (4)采用本文提出的計算方法可準確有效地預測艦船在航行時的水下輻射噪聲。后續可深入探究艦船在不同航速下,波浪的特征波高、波長等因素對其輻射噪聲的影響規律。

1.3 聲固耦合有限元方程

2 Wigley型護衛艦及其航行流場數值計算
2.1 Wigley型護衛艦結構與振動模型

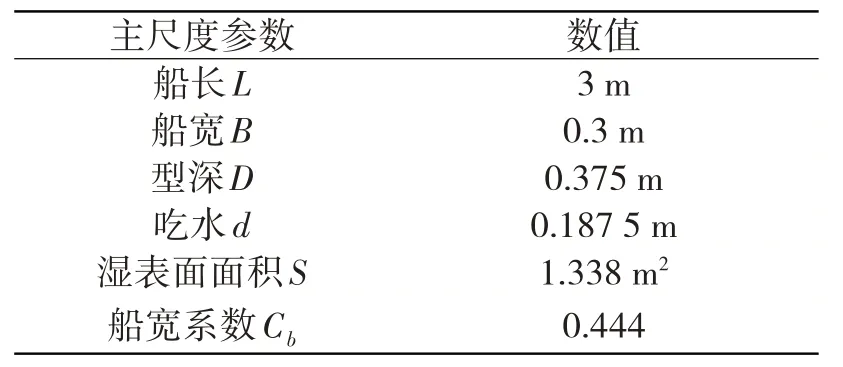



2.2 Wigley型護衛艦靜水航行繞流流場數值計算

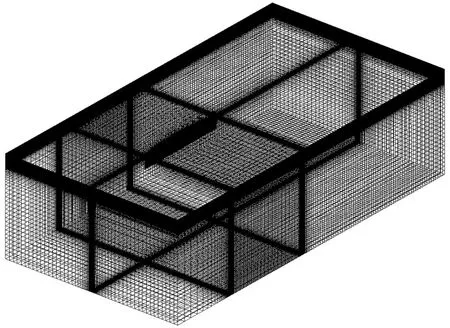


3 考慮自由液面波形的Wigley型護衛艦聲學計算方法

4 Wigley護衛艦水下輻射噪聲計算結果分析

5 結 論

