基于復變函數解法的桁材開孔腹板彈性屈曲分析

楊 源，莫中華，唐文勇，孫啟榮，沈亞明

（1.南通中遠海運川崎船舶工程有限公司，江蘇南通226005；2.上海交通大學海洋工程國家重點實驗室，上海200240）

0 引 言

在船體梁總縱彎矩作用下，甲板縱桁和船底縱桁承受較高的軸向壓力，結構設計時要確保它們具有足夠的屈曲強度。但是，出于人員、管路穿行和結構減重的目的，縱桁的腹板上不可避免地會布置一些開孔。開孔形狀以腰圓形和圓形較為常見，孔尺寸相比板格短邊長一般較大，此時開孔對板格屈曲強度的影響值得關注。由于開孔的存在，結構分析域的形狀變得不規(guī)則，面內應力發(fā)生了重分配，依靠純解析方法難以準確處理該問題。

早期，Schlack[1]采用Ritz法研究了中心開圓孔的矩形板格受壓屈曲問題，在小孔徑、方形板條件下的計算結果與試驗結果大體接近，這種模型過于理想化，實用價值有限。近年來，El-Sawy[2]、褚洪[3]、李政杰[4]等采用有限元法研究了開孔板彈性屈曲壓力的各種敏感性因素。潘祖興[5]以復變應力函數重構法配合區(qū)域劃分法研究了帶矩形開孔的矩形板屈曲，結果準確性高，只是區(qū)域分解法更適于通過簡單分解即可獲得較規(guī)則子區(qū)域形狀的開孔結構域，不易推廣到其他開孔形狀的情形。本文聚焦船體結構中常見的開腰圓孔矩形板格的板邊受壓彈性屈曲問題，以復變函數方法完成開孔板平面應力計算，以基于背景網格的Ritz法計算彈性屈曲載荷，形成了一種有別于有限元的半解析算法，可應用在船體結構設計校核中。

1 開孔板的平面應力計算

待分析問題的力學模型如圖1所示，在矩形板的中部存在一個腰圓形的開孔，開孔板的外板邊可能受到單向或兩向的壓應力作用，不考慮體力作用。開孔板的長、寬、厚分別標記為a、b、t，孔的長軸、短軸的長度分別標記為lx、ly，孔心位置以坐標( xh,yh)來表示，E、μ 為板材料的彈性模量和泊松比。計算開孔板格屈曲首先要確定板上任意一處位置的平面應力狀態(tài)量( σx,σy,τxy)。

根據Muskhelishvili提出的復變函數解法[6]，體力為0 時，均勻各向同性材質下的彈性平面問題的應力狀態(tài)解可由兩個復解析函數φ( z )和ψ( z )決定。各向應力、面內位移與φ( z )、ψ( z )之間存在如下的關系：

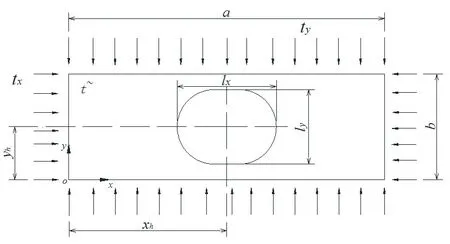
圖1 分析模型示意圖Fig.1 Diagram of analytical model

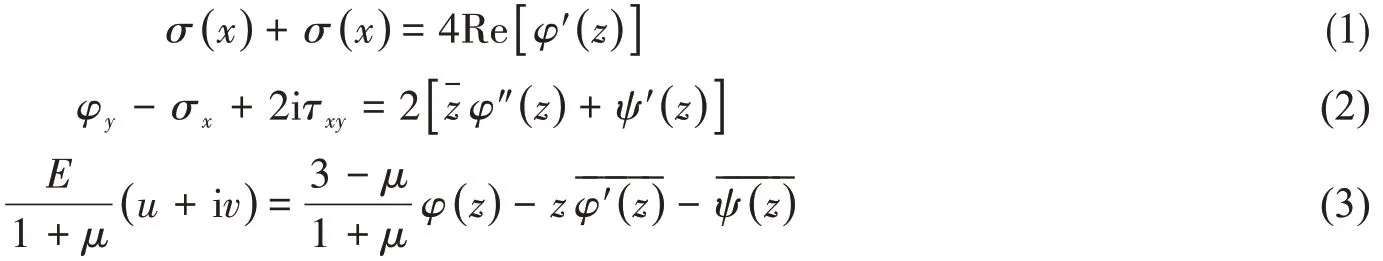
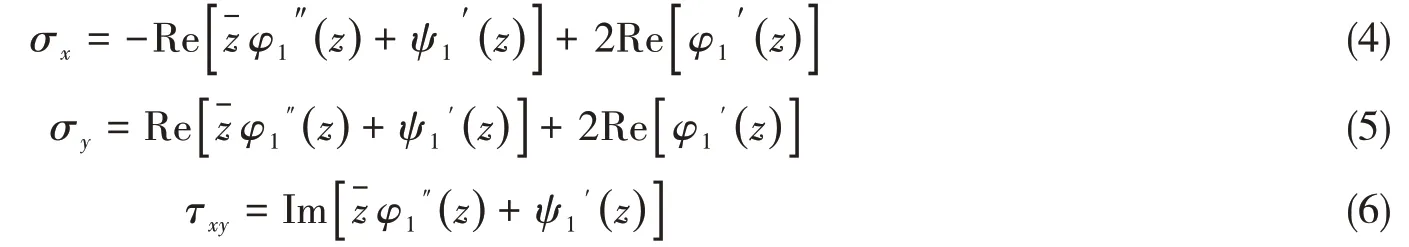
對于非圓形孔口的計算一般要進行保角變換處理，將彈性體在z平面上所占的區(qū)域變換為平面上以ξ = 0 為原點，1 為半徑的單位圓內部區(qū)域，此時的保角變換關系可表示為z = f( ξ )。將其代入φ1( z)和ψ1( z )中，z的函數變?yōu)棣蔚暮瘮担瘮档膯沃到馕鲂再|不變，有

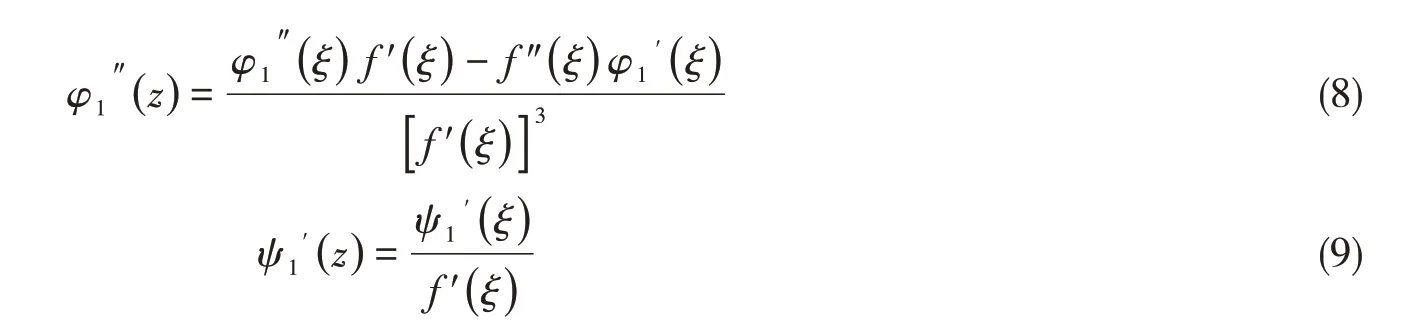
根據復變函數理論，在環(huán)形區(qū)域內單值解析的函數可展開成Laurent 級數，且這種展開應是唯一的。故可設：

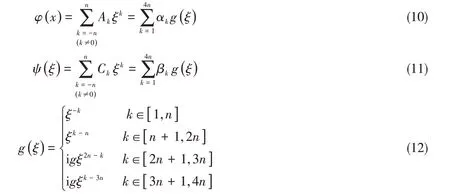
（10）-（11）式中，Ak和Ck為復常數，k= 0對應的常數項對分析無影響，可不考慮。為編程方便，上式進一步轉化為函數g( ξ )的線性組合，未知量變?yōu)閷嵆郸羕和βk，共8n個。

采用最小二乘邊界配點法[5-9]，構建邊界條件的限制方程。邊界面力tx，ty與應力σx,σy,τxy的關系如下：

式中，nx和ny為邊界法矢的方向余弦。本模型包括內外兩部分邊界，內邊界為腰圓形孔邊，邊界面力為0，外邊界為矩形，邊界面力為法向壓力。將內、外邊界等距離散為M個點，在每個點j上，用resj表示x,y兩個方向上應力殘差的平方和：

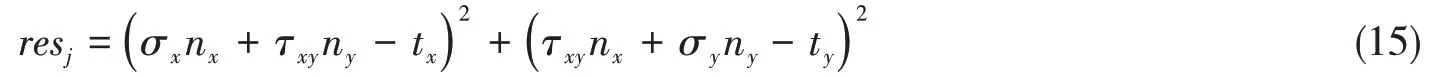
最接近精確解答的參數{ αk} ，{βk} 應使各點處的resj之和最小，故有

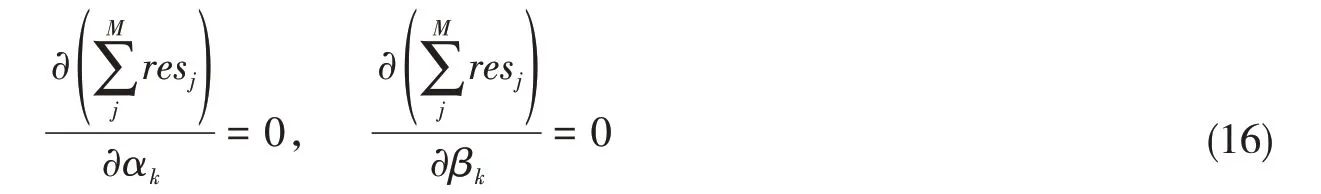
上式形成8n個線性方程，以求解未知參數{αk} ，{ βk} ，k為1至4n的整數，從而進一步確定結構域內每一點處的平面應力狀態(tài)量。

2 開孔矩形板的彈性屈曲分析

假設在板邊的面內壓力作用下，開孔板正處于中性平衡狀態(tài)。擾動引起結構發(fā)生偏離初始構形的微彎，結構域Ω內任一點( x,y )的撓度記為w，假設：

式中，Aj為未知常數，qj( x,y )為滿足結構位移邊界條件的基函數。基函數的選取與板的面外邊界條件有關，本文主要關注四邊簡支情況，不妨繼續(xù)采用經典矩形板的基函數構造形式：

此時，腰圓孔的出現(xiàn)增加了一道內圈的孔邊界，模型的孔邊是完全自由的，撓度未受限制，因此（18）式是滿足位移邊界條件的，但孔邊彎矩和剪力均為0，這兩項力邊界條件則不再能夠通過假設的基函數自動滿足。因此為獲得較準確的結果，需要增加N的數目，后面的算例說明22項的基函數組合已可獲得足夠準確的解。

開孔板的彎曲變形能Vε可表達為

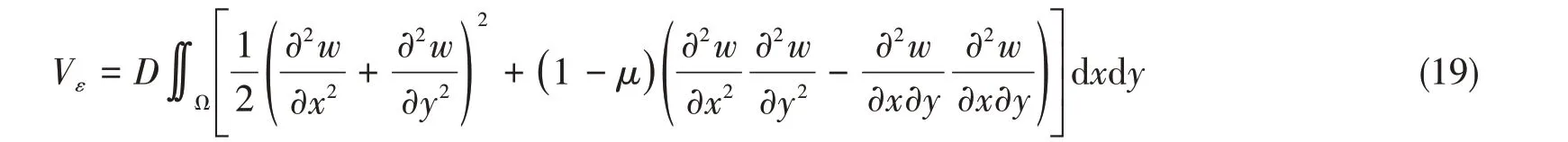
而在板邊單位壓力作用下外力功W為

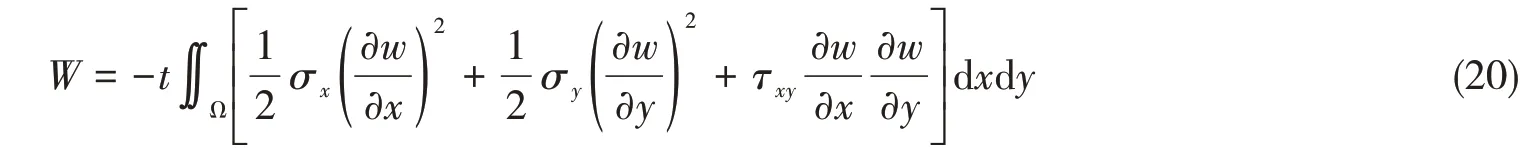
式中，D = Et3/[ 12( 1 - μ2)]，表示板的撓曲剛度。結構位能U = Vε- λW，λ代表施加的板邊壓力載荷。根據位能駐值原理，有

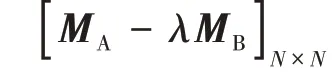
中性平衡狀態(tài)下板結構撓度解的不唯一，表現(xiàn)為方程組系數矩陣的奇異，使屈曲臨界載荷的計算轉化為矩陣特征值的計算。對開腰圓孔的矩形板，板內各處的平面應力σx，σy和τxy不再是簡單的均勻分布或線性分布關系，積分域Ω 的形狀也是不規(guī)則的。顯然，直接從整體的積分域出發(fā)來計算（22）-（23）式的積分比較困難，因此將結構域離散為三角形來實施積分計算。

這時結構域離散生成的網格屬于背景網格，不影響板結構撓曲面的連續(xù)性。在離散得到的三角形積分域內可使用二維Gauss積分方法計算積分，矩陣MA，MB的元素可表示為

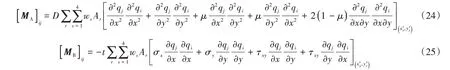
上式采用二維四點Gauss 積分公式[10]，ws為第s 個積分點的權重，Ar為離散得到的編號為r 的三角形面積，(,)為編號r 的三角形中第s 個積分點在總體坐標系下的坐標。每個積分點位置處的面內應力σx、σy，τxy由上一節(jié)所述的平面應力計算方法確定。

3 典型算例分析

參照圖1 取一典型的船體桁材板格，ls= 0.8 m，ly= 0.6 m，a = 2.55 m，b = 0.85 m，t = 0.01 m，孔的中心與板的中心重合，矩形板的長板邊不受面力，短邊受1 MPa的均布壓力。平面應力計算時，短板邊等分為20段，長板邊等分為60段，腰圓形孔邊按1/4圓弧長等分20段的密度離散，然后取每一段的中點位置作為邊界計算的配點，Laurent展開的參數n取30。計算在Matlab 7.7下編程實現(xiàn)。開孔腰圓孔的保角變換參照文獻［11］的做法進行，獲得的保角變換關系如（26）式，變換前后的內外邊界線見圖2。

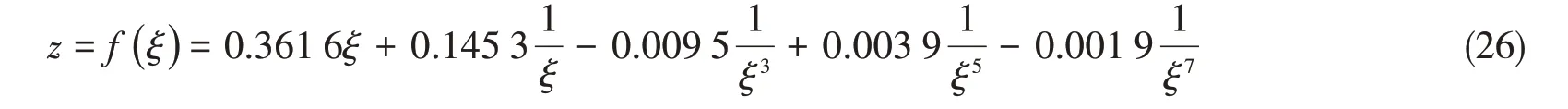
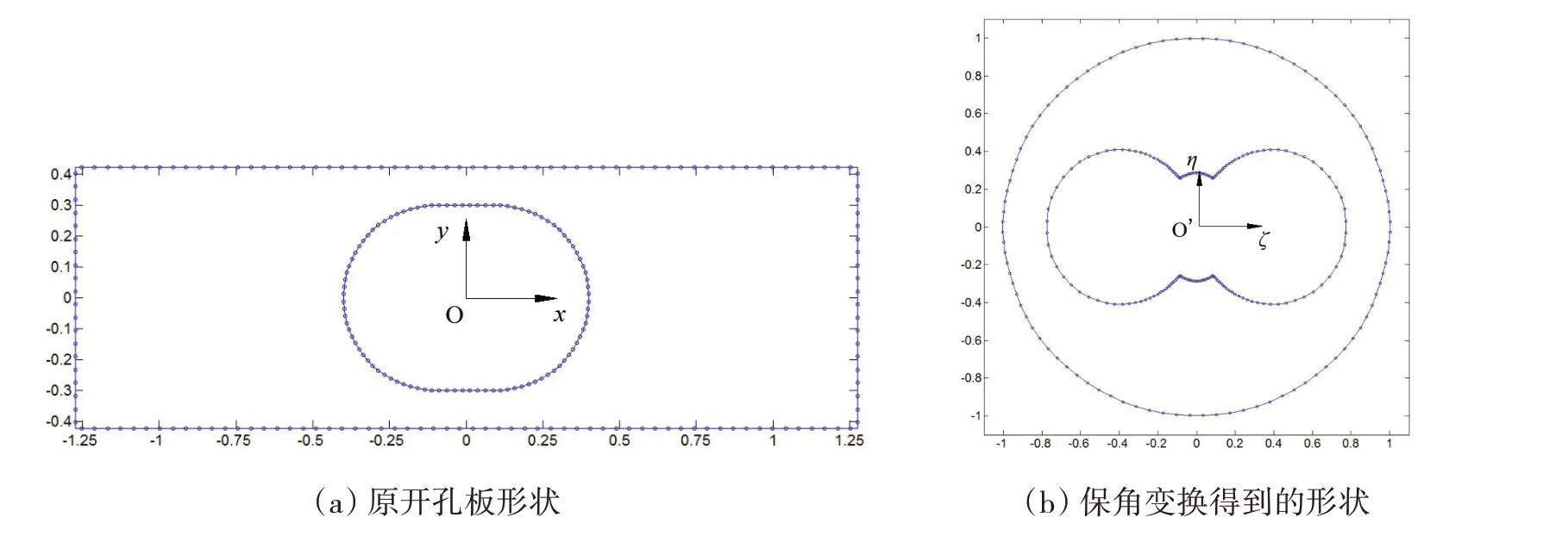
圖2 保角變換示意圖Fig.2 Diagram of conformal transformation

Matlab 編程計算開孔板的平面x 向應力如圖3 所示。考慮到應力分布的對稱性，在如圖4 所示的1/4 對稱腰圓孔邊上，取弧長等分點處的孔邊切向應力σθ結果，與ABAQUS 6.10 下的有限元平面應力解對比，顯示于表1。作為對比基準用的開孔板格有限元模型，腰圓孔邊網格尺度取0.012 m，外矩形板邊網格尺度取0.025 m，在兩者間的區(qū)域網格尺度逐漸過渡，以確保得到的孔邊應力足夠準確。表1中除了序號為7、8 的兩個計算點由于應力結果的絕對值較小而反映出較大的相對誤差外，其他11 個計算點的相對誤差率均在4%以內。考慮到應力集中效應在孔邊最大，開孔板上其他位置處應力的誤差將更小，可見復變函數解法的開孔板格應力計算是比較準確的。

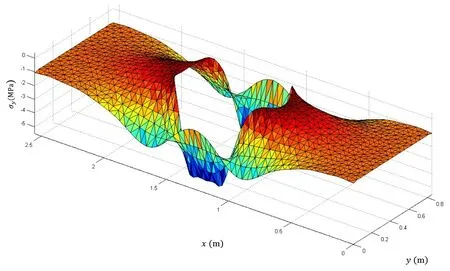
圖3 短邊受壓下的開孔板σy應力云圖 Fig.3 σy stress contour of perforated plate under longitudinal axial compression

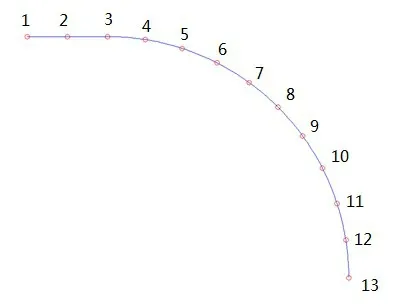
圖4 孔邊應力σθ計算點示意圖Fig.4 Diagram of calculation points for tangential stress σθ around the oval hole

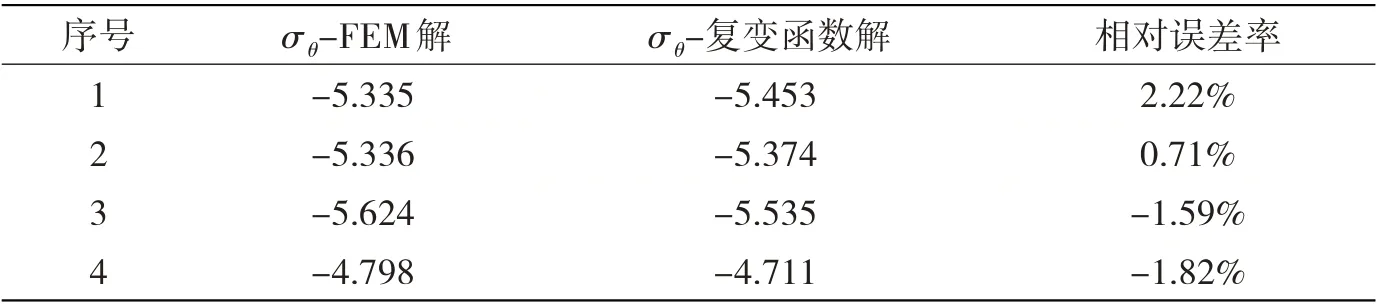
表1 孔邊應力σθ計算對比Tab.1 Comparison of tangential stress σθ around the oval hole

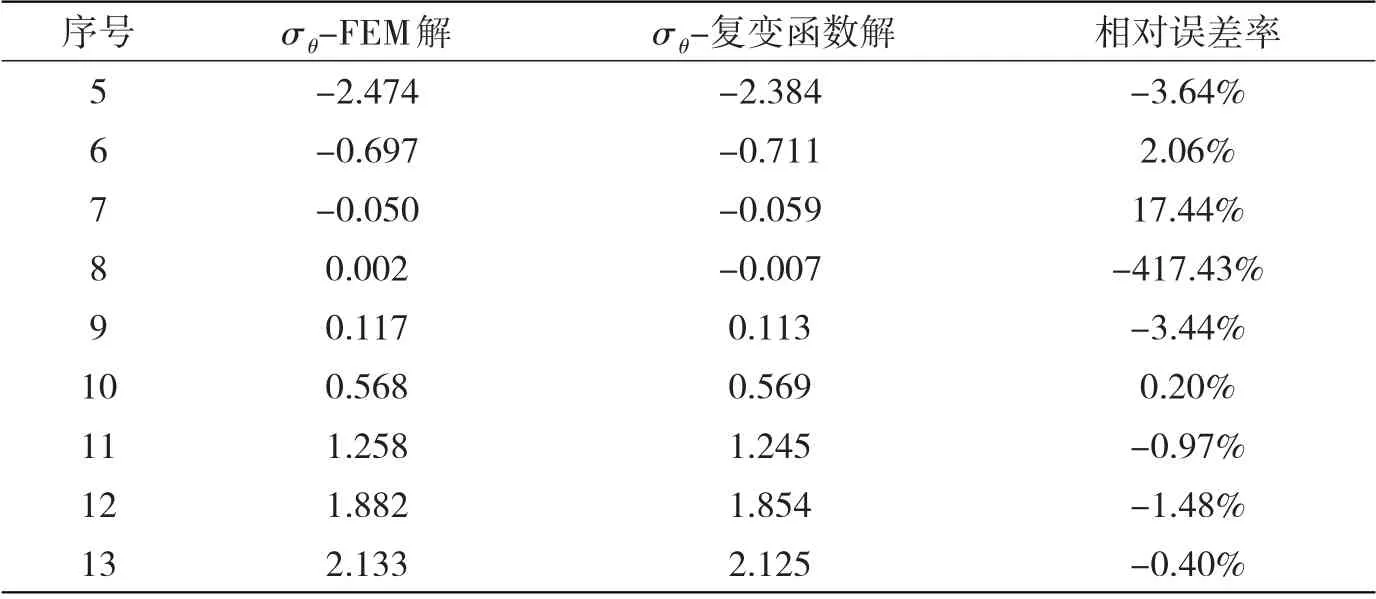
續(xù)表1

屈曲載荷計算環(huán)節(jié)的域網格離散采用較粗的三角形網格，基于Delauney 三角化方法實現(xiàn)，如圖5所示。計算采用（24）式的構造形式，以22 項基函數的線性組合來近似板的撓曲面，具體參數見表2。

有限元特征值屈曲作為對比方法，在ABAQUS 6.10 下建立2 種網格的有限元模型。第一種如圖6 所示，為global mesh size=0.05 m 下以Free 方式劃分得到的有限元網格模型，以四邊形單元（S4R）為主，輔以三角形單元（S3），記作有限元模型I。這種網格較密且均勻，經過驗證更密的網格對計算結果影響已經比較微弱，可認為這種網格密度下的分析結果準確度是足夠的，以此作為對比的基準模型。第二種采用如圖4 所示的三角形背景網格，生成三角形單元（S3）離散的有限元模型，記作有限元模型II。兩種有限元模型在加載時均采用shell edge load 方式施加板邊的面內壓力，并在矩形的3 個頂點處施加適當的面內約束，限制模型的剛體位移，特征值屈曲計算選用蘭索斯迭代算法完成。

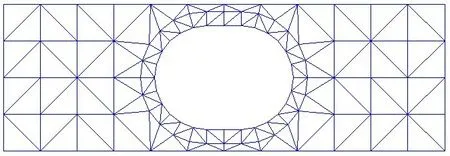
圖5 算例采用的積分背景網格Fig.5 Integration background mesh of the example

圖6 對比用的有限元模型Fig.6 Finite element model for comparison

表2 算例采用的基函數序列Tab.2 Basis functionse quence of the example

表3 算例的對比結果Tab.3 Comparison of results for the examples

計算結果如表3 所示，本文方法的屈曲臨界壓力解與有限元模型I 解比較接近，存在-0.56%的誤差。本文方法得到的1 階屈曲變形模態(tài)如圖7 所示，亦與有限元模型I的基本一致。負偏差則可能來自域離散的數值積分，這一點通過加密背景網格的驗算可初步驗證。若將M2背景網格的密度分別增加為原來的2 倍和3 倍，相應的彈性屈曲解分別為116.92 MPa 和116.89 MPa，與有限元模型I 的解已非常接近。而有限元模型II 的解則出現(xiàn)了7%以上的明顯結果偏差，這反映出背景網格和有限元網格存在著明顯差別。

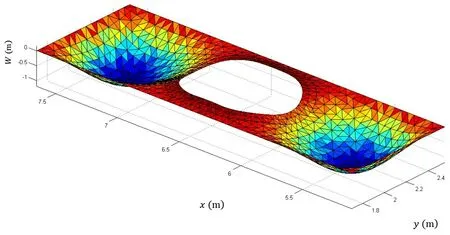
圖7 本文方法獲得的一階屈曲模態(tài)變形Fig.7 First-order buckling mode deformation obtained by this method

有限元方法采用分片位移場假設，網格離散對位移場連續(xù)性的削弱在網格較稀疏時會引起明顯的誤差，需要通過足夠密的網格來保證精度。而本文方法在平面應力和屈曲載荷計算中均采用了完全連續(xù)的位移場假設，網格的離散只是為了不規(guī)則形狀域下的數值積分計算，故本文方法對于網格離散的依賴度較低。

4 敏感性對比驗證

在展示開孔板格彈性屈曲載荷敏感性的同時，本章進一步展示本文方法的準確性。敏感性對比計算中，均采用與上一節(jié)相似的網格離散。

首先，通過設定不同的x、y 向板邊壓應力比，可獲得如圖8 所示的彈性屈曲結果曲線。以ABAQUS 解為基準，本文方法的結果誤差率在2%以內。誤差率隨著長邊受壓比重的增加有微弱增加。板格在短邊受壓為主時，可獲得較高的屈曲承載能力，故這種情況在船體結構校核上也更常見，下面的計算主要針對短邊受壓情形展開對比。

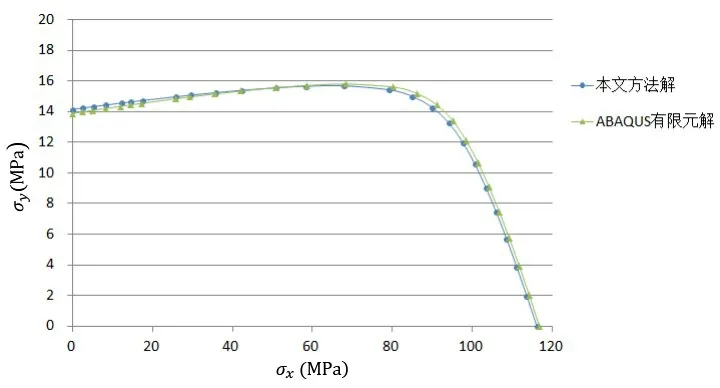
圖8 雙向軸壓作用的彈性屈曲解Fig.8 Elastic buckling solution under bi-axial compression

將腰圓孔沿x軸方向朝左側逐漸移動，分別計算xh從1.275 m逐步減小至0.575 m的彈性屈曲壓力解，結果如表4。當xh大于0.675 m時，本文方法與ABAQUS有限元解的吻合度較好，以ABAQUS解為基準，本文方法的結果誤差率保持在1%以內。當開孔距離孔邊較近時，本方法的誤差開始增大，這與有限的基函數選取不能反映過于局部化的撓曲變形有關。

表5～7分別反映了腰圓孔形狀、矩形板長度a和寬度b的變化對屈曲臨界載荷的影響，以ABAQUS解為基準，本文方法的結果誤差率均在1%以內。可以看出，以腰圓孔倍率表示腰圓孔長軸長度與短軸長度之比，腰圓孔倍率越高，彈性屈曲解也越大；彈性屈曲解隨矩形板長度a的增大而逐漸減小，但a>2.85 m后，彈性屈曲解的減小幅度已十分微弱；彈性屈曲解隨矩形板寬度b的增大而逐漸減小。

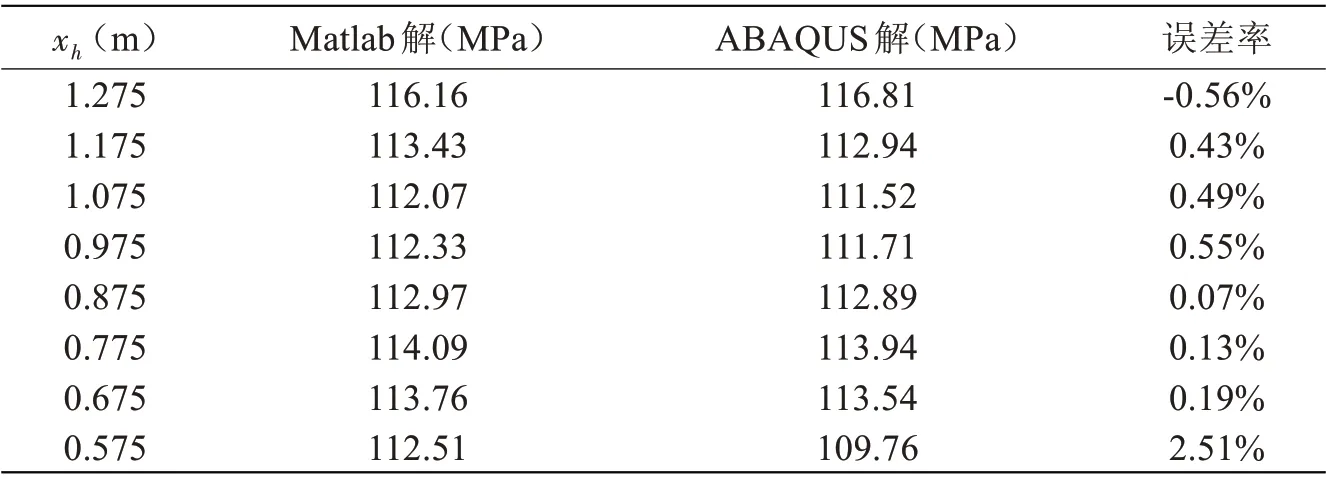
表4 腰圓孔位置的敏感性效應Tab.4 Sensitivity to oval cut-out location

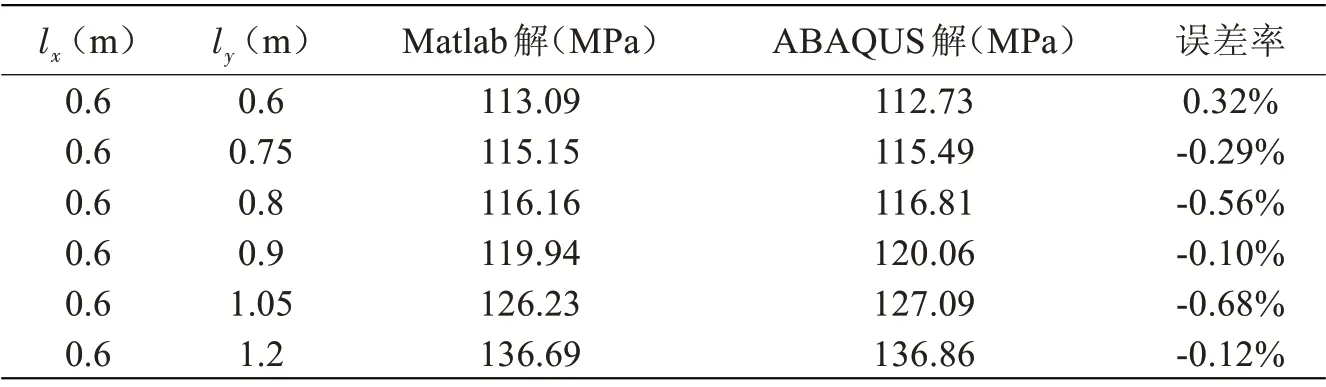
表5 腰圓孔倍率的敏感性效應Tab.5 Sensitivity to oval cut-out shape

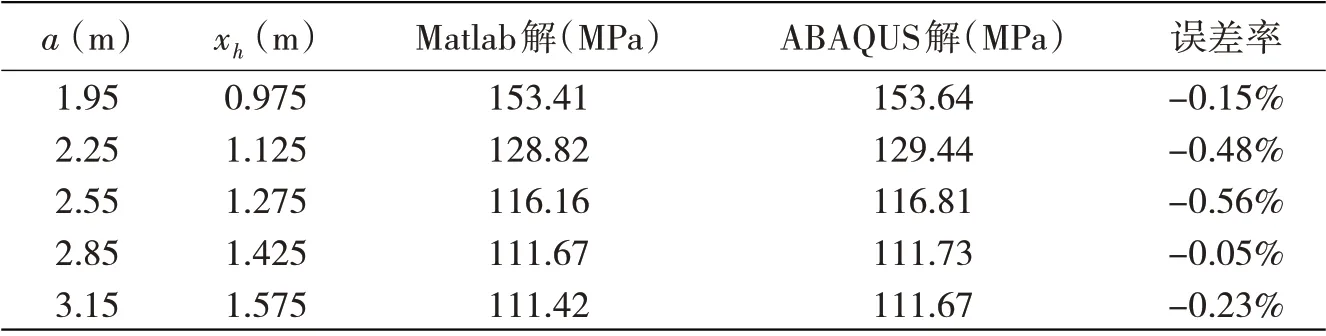
表6 矩形板長邊長度a的敏感性效應Tab.6 Sensitivity to rectangular plate long-side length

表7 矩形板短邊長度b的敏感性效應Tab.7 Sensitivity to rectangular plate short-side length

5 結 語

對船體桁材開孔腹板的屈曲問題，本文提出以改進的復變函數方法計算板內的平面應力，結合背景網格積分下的Ritz 法，確定開孔板格的彈性屈曲載荷。該方法基于完全連續(xù)的面內和面外位移場假設，對網格的依賴性相比有限元已有明顯的削弱，可以在較粗的域離散網格下獲得十分準確的彈性屈曲解。通過與ABAQUS 屈曲有限元結果的系列對比，本方法能夠較好地反映雙向受壓、孔位移動、腰圓孔倍率、矩形板長度和寬度變化的敏感性影響，具有良好的結果精度，可用于設計階段船體桁材開孔板格的屈曲校核。